Даны две окружности. Требуется найти все их общие касательные, т.е. все такие прямые, которые касаются обеих окружностей одновременно.
Описанный алгоритм будет работать также в случае, когда одна (или обе) окружности вырождаются в точки. Таким образом, этот алгоритм можно использовать также для нахождения касательных к окружности, проходящих через заданную точку.
- Количество общих касательных
- Алгоритм
- Реализация
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Общие касательные
- 🎦 Видео
Видео:Уравнение общей касательной к графикам функций.Скачать
Количество общих касательных
Сразу отметим, что мы не рассматриваем вырожденные случаи: когда окружности совпадают (в этом случае у них бесконечно много общих касательных), или одна окружность лежит внутри другой (в этом случае у них нет общих касательных, или, если окружности касаются, есть одна общая касательная).
В большинстве случаев, две окружности имеют четыре общих касательных.
Если окружности касаются, то у них будет три обших касательных, но это можно понимать как вырожденный случай: так, как будто две касательные совпали.
Более того, описанный ниже алгоритм будет работать и в случае, когда одна или обе окружности имеют нулевой радиус: в этом случае будет, соответственно, две или одна общая касательная.
Подводя итог, мы, за исключением описанных в начале случаев, всегда будем искать четыре касательные. В вырожденных случаях некоторые из них будут совпадать, однако тем не менее эти случаи также будут вписываться в общую картину.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Алгоритм
В целях простоты алгоритма, будем считать, не теряя общности, что центр первой окружности имеет координаты 
. (Если это не так, то этого можно добиться простым сдвигом всей картины, а после нахождения решения — сдвигом полученных прямых обратно.)
Обозначим через 
и 
радиусы первой и второй окружностей, а через 
— координаты центра второй окружности (точка отлична от начала координат, т.к. мы не рассматриваем случае, когда окружности совпадают, или одна окружность находится внутри другой).
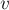
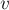
Для решения задачи подойдём к ней чисто алгебраически. Нам требуется найти все прямые вида 
, которые лежат на расстоянии от начала координат, и на расстоянии от точки . Кроме того, наложим условие нормированности прямой: сумма квадратов коэффициентов 
и 
должна быть равна единице (это необходимо, иначе одной и той же прямой будет соответствовать бесконечно много представлений вида ). Итого получаем такую систему уравнений на искомые 
:
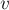
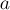
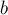
Чтобы избавиться от модулей, заметим, что всего есть четыре способа раскрыть модули в этой системе. Все эти способы можно рассмотреть общим случаем, если понимать раскрытие модуля как то, что коэффициент в правой части, возможно, умножается на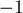 
.
Иными словами, мы переходим к такой системе:
Введя обозначения 
и 
, мы приходим к тому, что четыре раза должны решать систему:
Решение этой системы сводится к решению квадратного уравнения. Мы опустим все громоздкие выкладки, и сразу приведём готовый ответ:
Итого у нас получилось 
решений вместо 
. Однако легко понять, в каком месте возникают лишние решения: на самом деле, в последней системе достаточно брать только одно решение (например, первое). В самом деле, геометрический смысл того, что мы берём 
и 
, понятен: мы фактически перебираем, по какую сторону от каждой из окружностей будет прямая. Поэтому два способа, возникающие при решении последней системы, избыточны: достаточно выбрать одно из двух решений (только, конечно, во всех четырёх случаях надо выбрать одно и то же семейство решений).
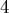
Последнее, что мы ещё не рассмотрели — это как сдвигать прямые в том случае, когда первая окружность не находилась изначально в начале координат. Однако здесь всё просто: из линейности уравнения прямой следует, что от коэффициента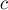 
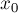
надо отнять величину 
(где 
и 
— координаты первоначального центра первой окружности).
Видео:Найдите уравнение обшей касательнойСкачать
Реализация
Опишем сначала все необходимые структуры данных и другие вспомогательные определения:
Тогда само решение можно записать таким образом (где основная функция для вызова — вторая; а первая функция — вспомогательная):
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:Построение общей внешней касательной к двум окружностямСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:8 класс, 32 урок, Касательная к окружностиСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Математика без Ху!ни. Уравнение касательной.Скачать  Общие касательныеВыясним сколько общих касательных имеют две окружности и как эти общие касательные могут быть расположены.
Если две окружности не пересекаются и окружность меньшего радиуса лежит внутри окружности большего радиуса, то они не имеют общих касательных.
В другом случае не пересекающиеся окружности имеют четыре общие касательные.
внешние общие касательные При этом, если обе окружности лежат по одну сторону от касательной (в одной полуплоскости), то такая касательная называется внешней.
внутренние общие касательные Если окружности лежат по разные стороны от общей касательной (в разных полуплоскостях), то такая касательная называется внутренней.
Если две окружности имеют внутреннее касание, то у них есть одна общая касательная.
При внешнем касании две окружности имеют три общие касательные.
Две пересекающиеся окружности имеют две общие касательные. 🎦 ВидеоУравнение окружности (1)Скачать  Построение общей касательной к двум окружностямСкачать  Внешняя касательная к двум окружностямСкачать  К двум окружностям проведены общие касательныеСкачать  Составить уравнения касательных к окружности (x-1)2+(y+3)2=40, перпендикулярных прямой 3x+y-4=0Скачать  9 класс, 8 урок, Взаимное расположение двух окружностейСкачать  Планиметрия. Две касающиеся окружности с общей касательной. Задание 16 (41)Скачать  Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать  Два способа найти общую касательную к окружностям | Планиметрия ЕГЭ | Денис Жучков | СMBСкачать  Касательная к двум окружностям разного диаметра.Скачать  Касательные к двум окружностям.Скачать  Окружность, гипербола и общая касательная (Часть 1)Скачать  |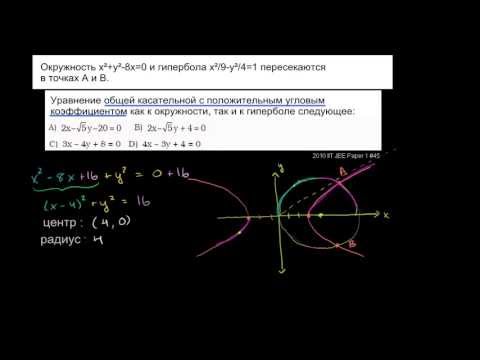
