Уравнение общего перпендикуляра к двум прямым в пространстве

Видео:Построение общего перпендикуляра к двум скрещивающимся прямым | Стереометрия #33 | ИнфоурокСкачать

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми

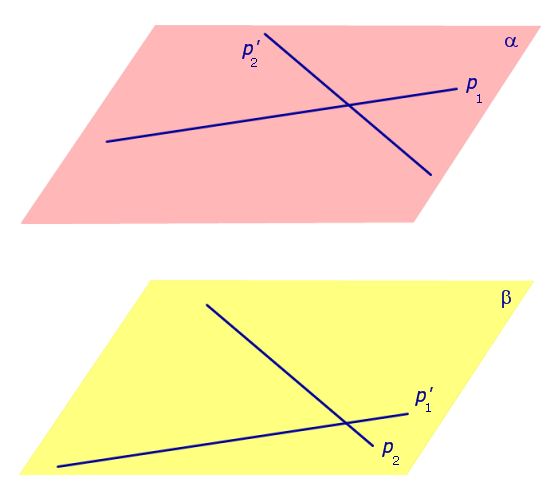
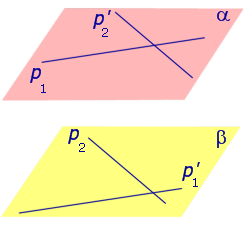
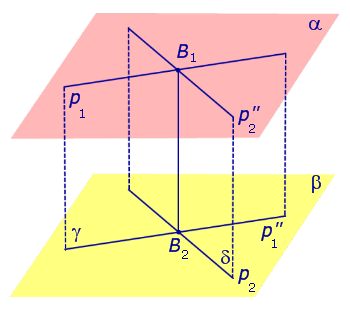
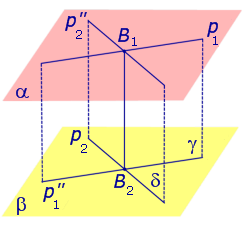
Теорема. Пусть p₁ и p₂ – две произвольные скрещивающиеся прямые скрещивающиеся прямые . Если рассмотреть всевозможные прямые A₁A₂, такие, что точка A₁ лежит на прямой p₁, а точка A₂ лежит на прямой p₂, то будут выполнены следующие два утверждения:

1. Среди всех прямых A₁A₂ существует единственная прямая, перпендикулярная к прямой p₁ и к прямой p₂ ( общий перпендикуляр к двум скрещивающимся прямым ).
2. Среди всех отрезков A₁A₂наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

Доказательство. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

Через произвольную точку прямой p₁ проведем прямую , параллельную прямой параллельную прямой p₂ , а через произвольную точку прямой p₂ проведем прямую , параллельную прямой параллельную прямой p₁ . Обозначим буквой α плоскость, проходящую через прямые p₁ и , а буквой β плоскость, проходящую через прямые p₂ и (рис 1).

Поскольку прямая p₁ параллельна прямой , лежащей на плоскости β , то по признаку параллельности прямой и плоскости прямая p₁ параллельна плоскости β. Точно так же, поскольку прямая параллельна прямой p₂ , лежащей на плоскости β , то прямая по признаку параллельности прямой и плоскости параллельна плоскости β. Таким образом, плоскость α содержит две пересекающиеся прямые p₁ и , паралельные плоскости β. В силу признака параллельности плоскостей заключаем, что плоскости α и β параллельны.

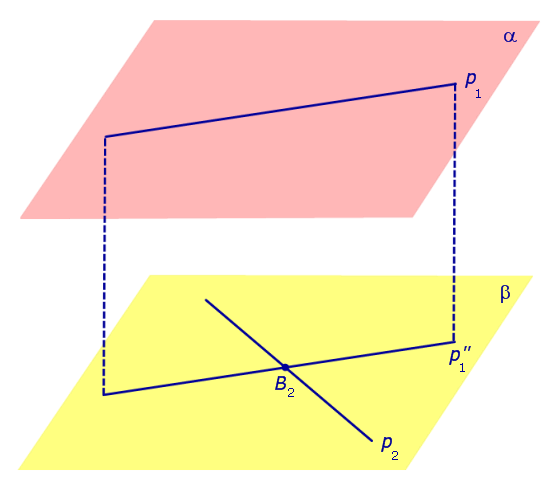
Спроектируем прямую p₁ на плоскость β. Получим прямую , являющуюся проекцией прямой проекцией прямой p₁, и обозначим точку пересечения прямых p₂ и буквой B₂ (рис. 2).

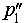
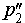
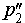
Спроектируем теперь прямую p₂ на плоскость α . Получим прямую , являющуюся проекцией прямой проекцией прямой p₂ , и обозначим точку пересечения прямых p₁ и буквой B₁ (рис. 3).

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

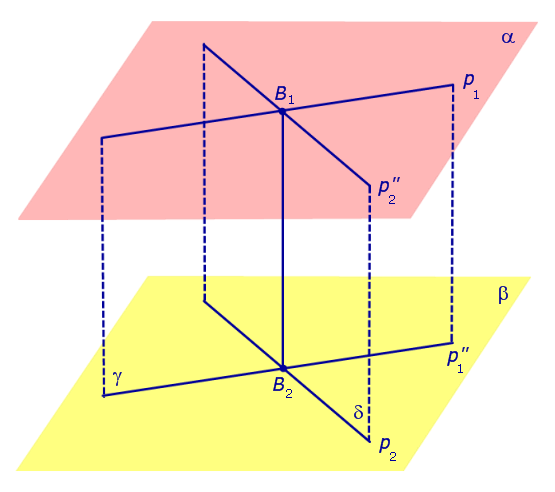
Докажем, что построенная прямая B₁B₂ является единственным общим перпендикуляром к прямым p₁ и p₂ .

Таким образом, общий перпендикуляр к прямым p₁ и p₂ является линией пересечения плоскостей γ и δ, то есть прямой B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

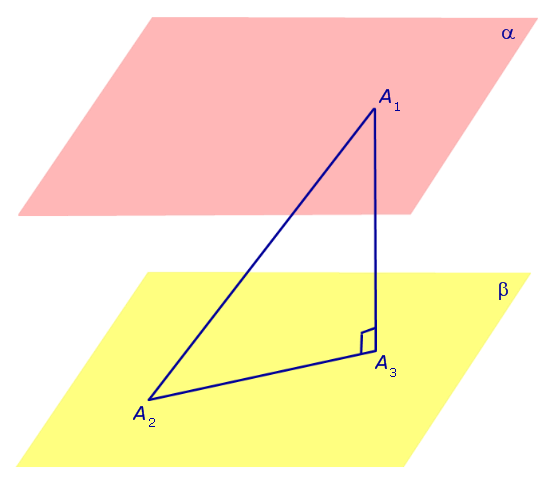
Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок A₁A₂ , у которого конец A₁ лежит на плоскости α , а конец A₂ лежит на плоскости β . Опустим перпендикуляр из точки A₁ на плоскость β и обозначим основание этого перпендикуляра символом A₃ (рис. 4).

Если отрезок A₁A₂ не является перпендикуляром к плоскостям α и β, то точка A₃ не совпадет с точкой A₂ , и треугольник A₁A₂A₃ будет прямоугольным треугольником с гипотенузой A₁A₂ и катетом A₁A₃. Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

Видео:11. Прямая в пространстве и ее уравненияСкачать

Математический портал

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Nav view search

Navigation

Search

• Вы здесь:
• Home

Видео:Расстояние между скрещивающимися прямыми и уравнение их общего перпендикуляра.Скачать

Расстояние между двумя скрещивающимися прямыми.

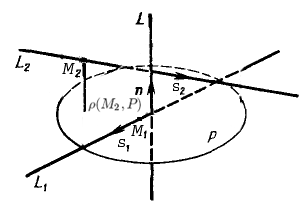
Пусть $L_1: frac=frac=frac$ и $L_2: frac=frac=frac$ — две скрещивающиеся прямые. Расстояние $rho(L_1, L_2)$ между прямыми $L_1$ и $L_2$ можно найти по следующей схеме:

1) Находим уравнение плоскости $P,$ проходящей через прямую $L_1,$ параллельно прямой $L_2:$

Плоскость $P$ проходит через точку $M_1(x_1, y_1, z_1),$ перпендикулярно вектору $overline n=[overline s_1, overline s_2]=(n_x, n_y, n_z),$ где $overline s_1=(m_1, l_1, k_1)$ и $overline s_2=(m_2, l_2, k_2)$ — направляющие вектора прямых $L_1$ и $L_2.$ Следовательно, уравнение плоскости $P: n_x(x-x_1)+n_y(y-y_1)+n_z(z-z_1)=0.$

2) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_2$ до плоскости $P:$

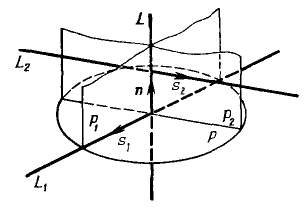
Нахождение общего перпендикуляра скрещивающихся прямых.

Для нахождения общего перпендикуляра прямых $L_1$ и $L_2,$ необходимо найти уравнения
плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0;$

Тогда уравнение общего перпендикуляра имеет вид

Пример.

2.214.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Решение.

а) Если прямые $L_1$ и $L_2$ лежат в одной плоскости, то их направляющие вектора $overline(3, 4, -2),$ $overline(6, -4, -1),$ и вектор $overline l,$ соединяющий произвольную точку прямой $L_1$ и произвольную точку прямой $L_2$ компланарны. В качестве такого вектора $overline$ можно выбрать $overline(x_2-x_1, y_2-y_1, z_2-z_1).$ Проверим будут ли эти вектора компланарны.

Следовательно, вектора не компланарны и прямые не лежат в одной плоскости.

б) Запишем уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1.$ Эта плоскость проходит через точку $M_2(21, -5, 2)$ перпендикулярно вектору $overline n=[overline s_1, overline s_2].$

Таким образом, вектор $overline n$ имеет координаты $overline n(-12, -9, -36).$

Находим уравнение плоскости $$P:,, -12(x-21)-9(y+5)-36(z-2)=0Rightarrow$$ $$Rightarrow-12x-9y-36z+252-45+72=0Rightarrow -12x-9y-36z+279=0Rightarrow$$ $$Rightarrow 4x+3y+12z-93=0.$$

в) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_1$ до плоскости $P:$

Ответ: $frac.$

г) Найдем уравнения плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Имеем, $M_1=(-7, -4, -3)in P_1,$

Таким образом, $$P_1: 54(x+7)-44(y+4)-7(z+3)=54x-44y-7z+378-176-21=$$ $$=54x-44y-7z+181=0.$$

Аналогично находим $P_2:$

Имеем, $M_2=(21, -5, 2)in P_2,$

Таким образом, $$P_1: -45(x-21)-76(y+5)+34(z-2)=-45x-76y+34z+945-380-68=$$ $$=-45x-76y+34z+497=0.$$

Ответ: $left<begin54x-44y-7z+181=0;\ -45x-76y+34z+497=0.endright. $

2.215.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Ответ: б) $4x+12y+12z+76=0;$

г) $left<begin53x-7y-44z-429=0;\ 105x-23y-48z+136=0.endright. $

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

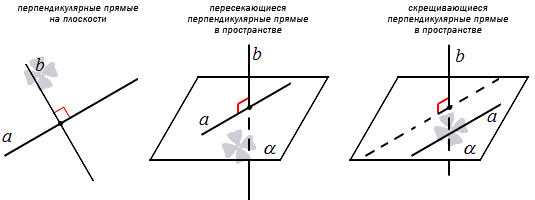
Перпендикулярные прямые, условие перпендикулярности прямых

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Перпендикулярные прямые – основные сведения

Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается « ⊥ », а запись принимает вид a ⊥ b , что значит, прямая a перпендикулярна прямой b .

Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые O x , O z , O y перпендикулярны попарно: O x и O z , O x и O y , O y и O z .

Видео:Уравнение прямой в пространстве. 11 класс.Скачать

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b .

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Пусть введена прямоугольная декартова система координат О х у с заданными уравнениями прямой на плоскости, которые определяют прямые a и b . Направляющие векторы прямых a и b обозначим a → и b → . Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a → и b → . Это возможно только при скалярном произведении векторов a → = ( a x , a y ) и b → = ( b x , b y ) равном нулю, а запись имеет вид a → , b → = a x · b x + a y · b y = 0 . Получим, что необходимым и достаточным условием перпендикулярности прямых a и b , находящихся в прямоугольной системе координат О х у на плоскости, является a → , b → = a x · b x + a y · b y = 0 , где a → = ( a x , a y ) и b → = b x , b y — это направляющие векторы прямых a и b .

Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b .

Заданы три точки A ( 8 , 6 ) , B ( 6 , 3 ) , C ( 2 , 10 ) в прямоугольной системе координат О х у . Определить, прямые А В и А С перпендикулярны или нет.

Прямые А В и А С имеют направляющие векторы A B → и A C → соответственно. Для начала вычислим A B → = ( — 2 , — 3 ) , A C → = ( — 6 , 4 ) . Получим, что векторы A B → и A C → перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

A B → , A C → = ( — 2 ) · ( — 6 ) + ( — 3 ) · 4 = 0

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Определить, заданные прямые x — 1 2 = y — 7 3 и x = 1 + λ y = 2 — 2 · λ перпендикулярны или нет.

Решение

a → = ( 2 , 3 ) является направляющим вектором заданной прямой x — 1 2 = y — 7 3 ,

b → = ( 1 , — 2 ) является направляющим вектором прямой x = 1 + λ y = 2 — 2 · λ .

Перейдем к вычислению скалярного произведения векторов a → и b → . Выражение будет записано:

a → , b → = 2 · 1 + 3 · — 2 = 2 — 6 ≠ 0

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a → , b → = a x · b x + a y · b y + a z · b z = 0 , где a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .

Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x 2 = y — 1 = z + 1 0 и x = λ y = 1 + 2 · λ z = 4 · λ

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a → = ( 2 , — 1 , 0 ) и b → = ( 1 , 2 , 4 ) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид a → , b → = 2 · 1 + ( — 1 ) · 2 + 0 · 4 = 0 .

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b , это и есть необходимое и достаточное условие.

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида A x + B y + C = 0 , уравнения прямой в отрезках вида x a + y b = 1 , уравнения прямой с угловым коэффициентом вида y = k x + b координаты векторов возможно найти.

Выяснить, перпендикулярны ли прямые 3 x — y + 2 = 0 и x 3 2 + y 1 2 = 1 .

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что n α → = ( 3 , — 1 ) — это нормальный вектор для прямой 3 x — y + 2 = 0 .

Упростим уравнение x 3 2 + y 1 2 = 1 до вида 2 3 x + 2 y — 1 = 0 . Теперь четко видны координаты нормального вектора, которые запишем в такой форме n b → = 2 3 , 2 .

Векторы n a → = ( 3 , — 1 ) и n b → = 2 3 , 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0 . Получим n a → , n b → = 3 · 2 3 + ( — 1 ) · 2 = 0 .

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y = k 1 x + b 1 , а прямая b — y = k 2 x + b 2 , отсюда следует, что нормальные векторы будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) . Само условие перпендикулярности сводится к k 1 · k 2 + ( — 1 ) · ( — 1 ) = 0 ⇔ k 1 · k 2 = — 1 .

Выяснить, перпендикулярны ли прямые y = — 3 7 x и y = 7 3 x — 1 2 .

Прямая y = — 3 7 x имеет угловой коэффициент, равный — 3 7 , а прямая y = 7 3 x — 1 2 — 7 3 .

Произведение угловых коэффициентов дает значение — 1 , — 3 7 · 7 3 = — 1 , то есть прямые являются перпендикулярными.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Определить, являются ли заданные прямые x — y — 1 = 0 и x 0 = y — 4 2 перпендикулярными.

Получаем, что нормальный вектор прямой x — y — 1 = 0 имеет координаты n a → = ( 1 , — 1 ) , а b → = ( 0 , 2 ) — направляющий вектор прямой x 0 = y — 4 2 .

Отсюда видно, что векторы n a → = ( 1 , — 1 ) и b → = ( 0 , 2 ) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t , чтобы выполнялось равенство n a → = t · b → . Отсюда вывод, что прямые не являются перпендикулярными.

🎬 Видео

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Видеоурок "Общие уравнения прямой"Скачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой по двум точкамСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать