Уравнение обращения воздействия (уравнение закона обращения воздействия), представляющее собой математическую запись закона обращения воздействия, было получено Л.А. Вулисом, и поэтому его часто называют просто уравнением Вулиса. Оно устанавливает связь между скоростью потока и физическими воздействиями.
В основе вывода уравнения обращения воздействия лежат основные уравнения газовой динамики, поскольку все виды воздействия так или иначе входят в них: изменение площади канала и расходное воздействие – в уравнение неразрывности или расхода, тепловое и механическое воздействия – в уравнение энергии (уравнение энтальпии), воздействие трения в виде гидравлических потерь – в уравнение Бернулли.
Решив совместно систему дифференциальных уравнений, включающую:
(1)
(2)
(3)
(4)
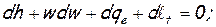
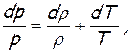
для анализа изменения скорости в результате геометрического (dF/F), расходного (dm/m), теплового (dqe), механического (dℓt) воздействий и воздействия трения (dℓr) получим
(5)
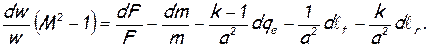
Уравнение обращения воздействия позволяет определить какой знак должно иметь то или иное воздействие для ускорения или торможения дозвуковых или сверхзвуковых потоков.
Закон обращения воздействия отражает усиливающееся влияние сжимаемости газа на его движение при увеличении числа Маха. При переходе через скорость звука (M=1) эти количественные изменения переходят в качественные – обращаются воздействия. Можно сказать, что закон обращения воздействия представляет собой пример проявления в газовой динамике более общего закона — закона перехода количества в качество.
Вывод уравнения Вулиса.
Существо вывода состоит в том, что в уравнении Бернулли (2) делаются замены величин, в результате которых в нем остаются только скорость– w, скорость звука – a и физические воздействия — dF, dm, dℓt, dℓr, dqe.
Это достигается путем замены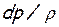 
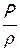
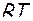
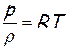
в уравнении Бернулли (2) его значением, найденным из уравнения состояния (4) . Для чего умножим правую и левую части равенства (4) соответственно на 
и на 
(это возможно – равенство сохраниться, поскольку для совершенного газа 
)
далее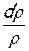 
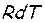
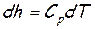
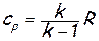
найдем из уравнения неразрывности (1)
— из уравнения энергии (3), которое после очевидной постановки 
и замены 
может быть записано как
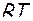
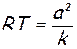
и, наконец, выразим через скорость звука ( 
)
.
Тогда уравнение Бернулли (2) поэтапно приобретает вид
Приведя подобные члены, соберем в левую часть все величины, содержащие скорость, а в правую — физические воздействия. После сокращения обеих частей на а 2 / k и замены w/a=М, получим
(5)
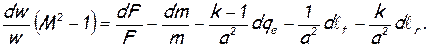
Формула (5) называется уравнением обращения воздействий. Оно выражает так называемый закон обращения воздействий. Согласно этому закону, для непрерывного изменения скорости газа в одну сторону за счет только одного физического воздействия необходимо, чтобы знак этого воздействия менялся на обратный в момент перехода через скорость звука. Если в процессе участвуют сразу несколько физических воздействий, то в момент перехода через скорость звука знак их суммы должен измениться на обратный.
Из уравнения обращения воздействий (5) легко получить пять частных случаев изменения скорости потока под влиянием какого–нибудь одного физического воздействия. Для этого в уравнении (5) все остальные воздействия надо положить равными нулю.
Так, например, если геометрическое воздействие dF≠0, а dm=dℓt=dℓr=dqe=0, то получается уравнение Гюгонио
которое уже было рассмотрено выше.
Если взять только одно расходное воздействие dm≠0, то уравнение (5) приобретает такой вид:
(6)
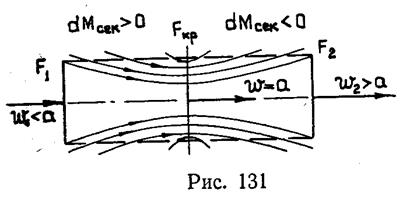
Течение, отвечающее этому уравнению, реализуется внутри расходного сопла. Его схема дана на рис. 131. Оно представляет собой трубу или канал постоянного сечения, имеющий на боковых стенках систему отверстий, через которые подводятся в основной поток дополнительные массы газа или отводятся из него.
Если на входе w1 0), то для согласования знаков левой и правой части уравнения (6) необходимо, чтобы dw>0. Таким образом, от входа до критического сечения скорость будет нарастать. В критическом сечении М=1, значит dm/m=0, т.е. расход в этом сечении проходит через максимум. За критическим сечением газ отбирается, расход уменьшается вдоль потока, т.е. dm 1, то из уравнения (6) получается, что dw>0.
Рассматривая рис. 131, можно заметить, что основной поток, т.е. масса газа, которая поступает в канал через входное сечение F1, имеет форму, напоминающую сопло Лаваля: сначала поток поджимается, в горле его сечение минимально, за горлом он расширяется. В отличие от геометрического сопла, в расходном поджатие основного потока происходит за счет дополнительной массы газа, которая оказывает вытеснительное действие. «Стенкой» для основного потока является в этом случае граница струи дополнительной массы газа. Изменение параметров основного потока, движущегося через расходное сопло, происходит по тем же законам, что и в случае обычного геометрического сопла.
Расходное сопло в том виде, как оно изображено на рис. 131, в технике не применяется, но его отдельные элементы встречаются довольно часто. При течении газа в смесителях, при подмешивании воздуха в зону горения в камерах сгорания, при отборе газа через отверстия в стенках канала и во многих других случаях наблюдается эффект расходного воздействия. Для получения сверхзвуковых потоков в небольших аэродинамических трубах, предназначенных для тарирования пневмометрических насадков и приборов, иногда применяют комбинированное сопло. Его дозвуковая часть представляет собой суживающееся геометрическое сопло, а сверхзвуковая — расходное сопло с отбором воздуха. Изменяя количество отбираемого воздуха, можно регулировать число М на выходе, сохраняя поток «чистым», без скачков.
Не следует смешивать расходное сопло и сопло с аэродинамическим поджатием потока. Схема последнего изображена в [2] на рис. 132.
Из ресивера 1 через щелевые сопла 2 газ высокого давления вдувается в основной канал, где поджимает основной поток, в котором образуется «горло». Поджатие здесь получается не за счет вытеснительного действия вдуваемого газа, а за счет его кинетической энергии. Между вдуваемой струей и стенкой образуется замкнутая вихревая зона 3. Количество вдуваемого газа в этом случае получается меньше, чем дополнительная масса, подаваемая в расходное сопло, поэтому «аэродинамическое» сопло экономичнее «расходного».
С помощью уравнения обращения воздействий (5) можно аналогичным способом проанализировать и другие виды воздействий. Они подробно рассмотрены в [2] и [8].
Видео:9 класс, 7 урок, Уравнение прямойСкачать
Уравнение обращения воздействий как общий случай одномерного течения газа.
Читайте также:
|
;
;
.
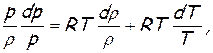
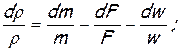
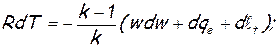
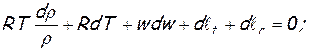
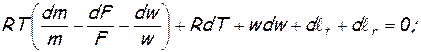
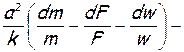
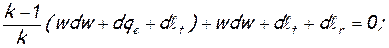
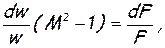
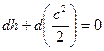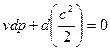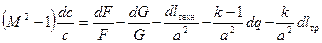