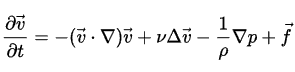Уравнение ньютона для вязкого трения

Главная > Документ

МЕХАНИКА БИОЛОГИЧЕСКИХ ЖИДКОСТЕЙ

Основные характеристики движения жидкости 1

Вязкость жидкости. Закон вязкого трения Ньютона 1

Ньютоновские жидкости 3

Ламинарный поток в цилиндрической трубке 4

Гидравлическое сопротивление 6

Распределение напряжения внутреннего трения 6

Неньютоновские вязкие жидкости 7

Методы определения коэффициента вязкости 10

Метод Стокса 10

Методы Оствальда и Гесса 11

Ротационный метод 12

Вопросы для самопроверки 16

Основные характеристики движения жидкости

Рассмотрим движение жидкости по трубе постоянного сечения.

Количество жидкости, протекающее через поперечное сечение в единицу времени называется расходом жидкости.

Различают объемный расход и массовый.

В разных точках живого сечения потока скорость частиц жидкости неодинакова. Поэтому в расчетах обычно используют среднюю скорость, которая равна отношению объемного расхода жидкости к площади живого сечения потока.

Движение жидкости является установившимся, или стационарным, если скорость частиц потока, а также все другие влияющие на его движение факторы (плотность, температура, давления и.т.д.), не изменяются во времени в каждой фиксированной точке пространства, через которую проходит жидкость. В этих условиях для каждого сечения потока расходы жидкости постоянны во времени.

Вязкость жидкости. Закон вязкого трения Ньютона

При движении реальной жидкости в ней возникают силы внутреннего трения, оказывающие сопротивление движению. Эти силы действуют между соседними слоями жидкости, перемещающимися друг относительно друга.

Свойство жидкости оказывать сопротивление усилиям, вызывающим относительное перемещение ее частиц, называется вязкостью.

При обтекании твердых поверхностей вязкой жидкостью происходит ее торможение, которое постепенно ослабевая, распространяется от стенки вглубь потока на некоторое расстояние δ, за пределами которого жидкость движется без значительных деформаций, и вязкие силы уже не играют существенной роли.

Скорость движения вязкие жидкости вблизи поверхности равна скорости движения поверхности.

Рассмотрим одномерное ламинарное течение вязкой жидкости между двумя параллельными пластинами (течение Куэтта), одна из которых движется относительно другой со скоростью под действием приложенной силы . Площадь пластин >> ширины зазора между пластинами. Профиль скоростей представлен на рисунке.

Экспериментально установлено, что величина силы внутреннего трения прямо пропорциональна площади поверхности слоя жидкостей и градиенту скорости — закон вязкого трения Ньютона.

Градиент скорости определяет величину изменения скорости на единицу расстояния при переходе от одного слоя жидкости к другому в направлении ОY, перпендикулярном направлению скорости движения слоев.

Сила внутреннего трения между слоями направлена противоположно направлению скорости более быстрого слоя и составляет:

, (1)

где – ко­эффициент динамический вязкости (далее — ко­эффициент вязкости).

Коэффициент вязкости численно равен силе трения, которая возникает между слоями жидкости единичной площади при градиенте скорости, равной единице.

Размерность коэффициента вязкости [Па∙с].

Преобразуем уравнение к виду:

(2)

где τ – напряжение внутреннего трения (касательное напряжение, или напряжение сдвига), действующее в плоскости соприкосновения смежных слоев жидкости;

– градиент скорости (скорость сдвига).

Размерность скорости сдвига [с –1 ].

Диапазоны градиентов скорости для некоторых материалов представлены в таблице.

Введение лекарства через шприц

Намазывание масла на хлеб

Выливание жидкости из бутылки

Выдавливание жидкого крема из пластикового тюбика

Нанесение губной помады

Нанесение лосьена через аэрозольный клапан

Ньютоновские жидкости

Жидкость, для которой коэффициент вязкости не зависит от условий течения, называется ньютоновской.

Зависимость напряжения внутреннего трения от градиента скорости называется кривой течения и для ньютоновской жидкости имеет вид прямой линии.

Пример 1

По твердой горизонтальной поверхности течет слой жидкости высотой h . Объемный расход жидкости через щель шириной a составляет Q , вязкость жидкости μ . . Определить напряжение внутреннего трения. Профиль скорости считать линейным по высоте.

Примем скорость жидкости на высоте , равной . Если профиль скорости считать линейным по высоте, то:

.

Элементарный объемный расход жидкости через прямоугольное сечение шириной a и высотой , площадью , составляет:

Интегрируя последнее уравнение от 0 до h, получим общий расход жидкости:

.

Скорость жидкости на высоте равна:

. (3)

Напряжение внутреннего трения равно:

. (4)

Ламинарный поток в цилиндрической трубке

Рассмотрим прямолинейное осесимметричное течение ньютоновской жидкости с вязкостью под действием перепада давлений р 1 – р 2 на участке цилиндрической трубки радиуса R и длиной L.

В результате действия сил трения, слои жидкости будут двигаться с разными скоростями.

При установившемся движении сумма проекций всех сил на ось потока равняется нулю. Исходя из этого условия, получено выражение для скорости как функции радиуса:

(5)

Скорость принимает максимальное значение на оси трубки, где r = 0.

(6)

Сопоставив выражение (5) и (6), находим:

(7)

Уравнение (7) выражает параболическое распределение скоростей в сечении трубопровода при установившемся ламинарном течении.

Для определения расхода жидкости при ламинарном движении рассмотрим элементарное кольцевое сечение с внутренним радиусом r и внешним радиусом (r+dr), площадь которого равна:

.

Объемный расход жидкости через это сечение составляет:

С учетом уравнения (5) объемный расход жидкости равен:

Интегрируя последнее уравнение от 0 до R, получим общий расход жидкости через трубку:

(8)

Уравнение (8) носит название формулы Пуазейля.

Средняя скорость в трубке равна:

С учетом уравнения (6)

(9)

Пример 2

Радиус кровеносного сосуда уменьшился в два раза. Во сколько раз изменится объемный расход жидкости через сосуд?.

Гидравлическое сопротивление

Рассмотрим формулу Пуазейля:

,

где — гидравлическое сопротивление.

Полученное уравнение аналогично закону Ома:

Объемный расход жидкости – аналог силы тока в проводнике; перепад давления =(р 1 –р 2 ) – аналог разности потенциалов на концах проводника; гидравлическое сопротивление – аналог электрического соапротивлению .

Таким образом, для моделирования гидродинамических процессов можно использовать электрические модели.

Распределение напряжения внутреннего трения

По трубке с внутренним радиусом R движется ламинарный поток жидкости с вязкостью и объемным расходом Q. Рассмотрим силы, действующие вдоль продольной оси х на элементарный цилиндр длиной dx и радиусом r:

Запишем уравнение равновесия:

.

Напряжение внутреннего трения, возникающее между слоями движущейся жидкости, равно: .

При , ;

при , .

На стенку трубки со стороны жидкости будет действовать напряжение равное , но в противоположном направлении, т.е.:

Формулу Пуазейля для цилиндра радиусом R и длиной dx можно представить в виде:

, откуда

Тогда, напряжение внутреннего трения на стенке трубки равно:

.

Распределение напряжения внутреннего трения в потоке линейно изменяется по радиусу:

. (10)

Неньютоновские вязкие жидкости

Многие жидкости в условиях одномерного сдвига имеют кривую течения, отличную от ньютоновской (Error: Reference source not found).

Характерные кривые течения нелинейно-вязких жидкостей

Вязкопластическими (бингамовскими) называют среды, течение которых начинается лишь после превышения некоторого критического напряжения , называемого пределом текучести. Кривая течения таких сред при отсекает на оси напряжений отрезок конечной длины, равной Величина характеризует пластические свойства материала, а наклон кривой течения к оси — её подвижность. Для бингамовских жидкостей уравнение кривой течения имеет вид: τ — τ 0 = μ П · dv / dn

где μ П — коэффициент пропорциональности, называемый пластической вязкость. Тангенс угла наклона кривой течения tg α= μ П

Смысл τ 0 – это напряжение, которое необходимо приложить для разрушения образовавшейся структуры из агрегатов, чтобы среда потекла.

Псевдопластичные жид­ кости начинают течь, как и ньютоновские, уже при самых малых значени­ях τ , однако для этих жидкостей отношение напряжения сдвига к градиенту скорости, называемое кажущейся вязкостью μ К , зависит от величины τ. Значения μ К снижаются с возрастанием dv / dn и кривая течения постепенно переходит в прямую с постоянным предельным наклоном μ ∞ (вязкость при бесконечно большом сдвиге). В логарифмических координатах функция dv / dn = f ( τ ) для псевдопластичных жид­костей в широких пределах изменения переменных (кроме крайнего участка, где μ К = μ ∞ ) близка к линейной и, мо­жет быть выражена зависимостью

τ = k ( dv / dn ) m

где k и т — константы. Величина k возрастает с увеличением вязкости и является мерой консистенции жидкости Величина т меньше 1 (между 0 и 1), причем чем меньше значение т., тем значительней отличается течение псевдопластичной жидкости от ньютоновской (для последней т =1 и, следовательно, k = μ ).

Характер изменения μ К для псевдопластичных жидкостей, например для раство­ров многих полимеров или суспензий с асимметричными частицами, часто связан с ориентацией их частиц (молекул) в направлении перемещения жидкости Так, длин­ные молекулы полимеров как бы вытягиваются в параллельные одна другой цепочки при значительных скоростях сдвига; в результате величины ( dv / dn ) и τ становятся про­порциональными друг другу.

Итак, механизм псевдопластичности – снижение внутреннего трения с ростом скорости сдвига. Например, в крови с ростом клетки крови (эритроциты) ориентируются потоком и вытягиваются по направлению потока, а затем начинают вращаться (эффект гусеницы танка), что ведет к значительному снижению внутреннего трения (вязкости).

Дилатантные жидкости , в отличие от псевдопластичных, характеризуются возрастанием μ К с увеличением dv / dn . Для них также применима зависимость τ = k ( dv / dn ) m , но показатель степени m > 1. Дилатантные жид­кости менее распространены, чем псевдопластичные, и обычно представляют собой суспензии с большим содержанием твердой фазы.

Механизм дилатансии – распад частиц структуры среды, их дезориентация потоком и усиление столкновений, «сухое» трение между сталкивающимися частицами.

Реологические модели некоторых неньютоновских вязкопластических сред:

модель Шведова– Бингама

k – пластическая вязкость

Наиболее распространенная из них – модель Шведова-Бингама. Она предполагает наличие у покоящейся жидкости жесткой структуры, которая препятствует течению при напряжении, меньшем , и мгновенно полностью разрушается при напряжении, большем . Тогда среда течет как обычная ньютоновская жидкость при напряжении . Когда напряжение становится меньше , структура снова восстанавливается.

Методы определения коэффициента вязкости

Метод Стокса

При движении сферической частицы в вязкой жидкости возникают силы сопротивления. При небольших скоростях, когда за частицей нет вихрей, сила сопротивления обусловлена вязкостью жидкости. Слои жидкости, прилегающие к частице, увлекаются ею. Между этими слоями и следующими возникают силы трения. Согласно закону Стокса при движении сферической частицы в вязкой жидкости с небольшой скоростью, когда нет вихрей, сила сопротивления равна:

На частицу, движущуюся в жидкости в поле силы тяжести, действуют следующие силы: сила тяжести, выталкивающая сила и сила сопротивления. Причем направление силы сопротивления противоположно направлению движения частицы.

При равномерном движении в соответствии с первым законом Ньютона:

(11)

где – диаметр шарика, ρ 1 и ρ 2 – плотности частицы и жидкости.

Для определения вязкости по методу Стокса берут высокий цилиндрический сосуд с исследуемой жидкостью. Диаметр сосуда должен быть таким, чтобы шарик при падении не касался стенок и не возникали завихрения. На сосуде имеются две кольцевые метки А и В. Метка А соответствует той высоте, где движение шарика становится равномерным. Нижняя метка В нанесена для удобства отсчета времени.

Бросая шарик в сосуд, отмечают по секундомеру время t прохождения шариком расстояния L между метками. Так как υ = L / t, то формула (11) принимает вид:

.

С какой скоростью всплывает пузырек воздуха диаметром в сосуде, наполненном глицерином? Динамическая вязкость глицерина , плотность .

Плотность глицерина >> плотности воздуха.

Методы Оствальда и Гесса

Эти методы основаны на использовании формулы Пуазейля (8), согласно которой объем жидкости V , протекающей за время t по капиллярной трубке длиной L при ламинарном течении, определяется соотношением

, откуда

Намного удобнее пользоваться формулой Пуазейля для относительного определения коэффициента вязкости.

Возьмем две жидкости с известным коэффициентом вязкости и неизвестным . Измерим время истечения одинакового объема жидкостей через один и тот же капилляр, которое соответственно составляет и .

Записав формулу Пуазейля для каждой из жидкостей и разделив одно выражение на второе, получим:

.

Поскольку жидкость вытекает под действием силы гравитации, то и выражение для коэффициента вязкости принимает вид:

.

Следовательно, измерив время истечения жидкостей, а также использовав известные значения и одной из них, определим коэффициент вязкости другой.

Ротационный метод

Ротационный цилиндровый вискозиметр состоит из двух цилиндров. В зазор между ними помещают исследуемую жидкость.

Рис. __Профиль скорости и вязкости в измерительных системах Серле и Куэтта

Ротационные реометры (вискозиметры), основанные на принципе Серле, с измерительными ячейками типа коаксиальных цилиндров, конус-плоскость и плоскость-плоскость.

Внутренний цилиндр (ротор) вращается двигателем с постоянной или изменяющейся по программе скоростью, в то время как внешний цилиндр (стакан) неподвижен. Стакан снабжен рубашкой для точного термостатирования измеряемого образца. Движение внутреннего цилиндра приводит к течению жидкости, находящейся в кольцевом зазоре между внутренним и внешним цилиндрами. Сопротивление жидкости, которая подвергается сдвигу между неподвижной и движущейся поверхностями измерительной системы, приводит к возникновению на внутреннем цилиндре крутящего момента, связанного с вязкостью жидкости и направленного против крутящего момента двигателя. Индикатор крутящего момента фиксирует изменение крутящего момента.

Вращается с определенной скоростью внешний цилиндр. Вращение внешнего цилиндра вызывает течение жидкости в кольцевом зазоре. Из-за сопротивления жидкости, подвергаемой сдвигу, крутящий момент, пропорциональный вязкости жидкости, передается на внутренний цилиндр и также должен вызвать его вращение. Этот крутящий момент определяют, измеряя противодействующий крутящий момент, необходимый для того, чтобы внутренний цилиндр оставался неподвижным.

Визначити крутний момент, що виникає в результаті опору рідини в концентричному циліндровому віскозиметрі, заповненому цілісною кров’ю з в’язкістю . Зовнішній циліндр обертається з кутовою швидкістю рад/c, радіус внутрішнього циліндра r, проміжок між циліндрами h, довжина проміжку L.

Згідно з законом внутрішнього тертя напруження внутрішнього тертя становить

;

;

Таким образом, вязкость жидкости определяют по формуле:

,

M – крутящий момент,

D – внутренний диаметр наружного цилиндра,

h – зазор между цилиндрами,

L – длина зазора.

– угловая скорость внешнего цилиндра, рад.

Ротационный вискозиметре с измерительной ячейкой

Визначити градієнт швидкості (швидкість зсуву), що виникає у в’язкій рідині, розміщеній між конусом, який обертається з кутовою швидкістю , і нерухомою площиною. Кут між конусом і площиною становить.

Градієнт швидкості визначається як зміна швидкості по висоті кутового зазору. Висота зазору , для віскозиметру типу конус-площина, є функцією радіуса конуса і кута між конусом і площиною:

.

Швидкість руху в’язкої рідини у поверхні дорівнює швидкості руху поверхні, тобто швидкість руху рідини також є функцією радіуса конуса:

Градієнт швидкості дорівнює:

Визначити в’язкість рідини, що заповнює зазор між конусом і площиною, за наступних умов: частота обертання конуса 10 об/хв, кут між конусом і площиною 1,5 о , напруження зсуву 1, 918 Н/м 2 .

Визначимо кутову швидкість обертання конуса: .

Визначимо швидкість зсуву: .

Згідно з законом внутрішнього тертя, в’язкість рідини дорівнює:

Визначити крутний момент, що виникає в ротаційному віскозиметрі типу конус-площина в результаті опору рідини, яка піддається зсуву. Кутова швидкість обертання конуса , напруженні зсуву рідини , зовнішній радіус конуса , кут між конусом і поверхнею .

Крутний момент, що виникає в результаті опору рідини, яка піддається зсуву:

,

де — довжина твірної конуса, що відповідає довільному радіусу .

Вопросы для самопроверки

Что такое сила внутреннего трения?

Чем обусловлена вязкость жидкости и от каких параметров она зависит?

Укажите единицу СИ коэффициента вязкости.

Что такое градиент скорости? В каких единицах он изменяется?

Напишите уравнение Ньютона для течения вязкой жидкости.

Что такое ньютоновская и неньютоновская жидкости?

Выведите формулу для определения вязкости по методу Стокса.

Какие условия должны выполняться при измерении вязкости методом Стокса?

Какие силы действуют на шарик, движущийся в вязкой жидкости?

Формула Пуазейля, ее анализ.

Устройство цилиндрового вискозиметра Вывод расчетной формулы для определения вязкости.

Как изменяется напряжение внутреннего трения по сечению потока?

Видео:Три Закона Ньютона. Простое ОбъяснениеСкачать

Основные законы движения жидкостей и газов

Для расчета движения воды в трубопроводе нужно знать не так уж и много. Для этого не надо глубоко изучать физику, но всё же некоторое основные понятия изучить придется.

В этой статье я приведу самые основные формулы, которые вам пригодятся не только для расчетов, но и для общего понимания, что может влиять в вашем водопроводе на его течение. Иногда общее понимание процессов поможет вам избежать ошибок при монтаже системы.

Например, не все знают, что в части водопровода с трубами меньшего диаметра давление на стенки меньше, чем на участке с трубами большего диаметра. Почему возникает кавитация и вообще, что это такое. А это надо знать.

Статья будет обновляться и дополняться.

Видео:Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать

Уравнение неразрывности

Для жидкости, текущей в трубе, этот закон используют в такой форме (называемой уравнением неразрывности):

Где v — скорость жидкости S — площадь сечения трубы, по которой течёт жидкость. Сформулировать этот закон можно и так:

Сколько вливается жидкости в ёмкость, в данном случае в трубу, столько должно и выливаться, если условия течения не изменяются.

Скорость в узких участках трубы должна быть выше, чем в широких.

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Уравнение Бернулли стационарного движения

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 — 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.

Идеальная жидкость — жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.

Уравнение стационарного движения, носящее его имя, имеет вид:

где P — давление жидкости, ρ − её плотность, v — скорость движения, g — ускорение свободного падения, h — высота, на которой находится элемент жидкости.

Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.

В уравнении Бернулли есть три слагаемых:

• ρ⋅v 2 /2 — динамическое давление — кинетическая энергия единицы объёма движущей жидкости;
• ρ⋅g⋅h — весовое давление — потенциальная энергия единицы объёма жидкости;
• P — статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

Видео:Решение задач по теме Законы НьютонаСкачать

Явление кавитации

Кавитация (от латинского cavitas — «углубление», «полость») — процесс образования полостей (пузырьков) в движущейся жидкости вследствие понижения давления.

Явление кавитации также объясняется уравнением Бернулли. Если скорость течения жидкости значительно возрастает, то давление сильно понизится — настолько, что жидкость закипит. Такую скорость можно получить, если пропускать жидкость через очень узкий участок трубы или при быстром обращении лопатки в водяном насосе.

Пузырьки по ходу движения жидкости попадают в области жидкости с нормальным давлением и там схлопываются. Это схлопывание сопровождается гидродинамическими эффектами, способными привести к разрушению трубы или стенок насоса.

Видео:Три закона НьютонаСкачать

Гидродинамика Эйлера и Навье-Стокса

Уравнение Бернулли позволяет объяснить очень много интересных гидродинамических явлений, но гораздо больше явлений, происходящих в движущихся жидкостях и газах, с его помощью объяснить нельзя, потому что этот закон для идеальной жидкости, т.е для жидкости, которая не обладает внутренним трением, а значит не создает гидравлическое сопротивление..

Реальная жидкость отличается от идеальной и обладает внутренним трением, или по другому называют вязкостью. Два соприкасающиеся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый.

Видео:Третий закон Ньютона | Физика 9 класс #12 | ИнфоурокСкачать

Закон вязкого трения Ньютона

Ньютон предположил, что величина этой силы (называемой силой внутреннего трения) пропорциональна разности скоростей элементов жидкости. Следовательно, сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости:

η − коэффициент динамической вязкости.

Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются ньютоновскими, или жидкостями с линейной вязкостью.

Величину коэффициента динамической вязкости (и справедливость данного закона) Ньютон определил с помощью несложного опыта: он передвигал по поверхности жидкости пластинку с той или иной скоростью. Для того чтобы поддерживать эту скорость постоянной, требовалась сила, которая при небольшой глубине жидкости оказалась прямо пропорциональна площади S и скорости пластинки v и обратно пропорциональна глубине жидкости h:

И хотя при увеличении глубины жидкости h сила вязкого трения пластинки не становится исчезающе малой, эта формула довольно точно описывает взаимодействие между соприкасающимися элементами жидкости.

Чем больше разность скоростей, тем больше сила, с которой они воздействуют друг на друга, заставляя притормаживать слишком быстро движущиеся элементы и разгоняя слишком медленные.

В результате относительное движение в жидкости прекращается (но иногда это может произойти не очень скоро).

Видео:Сила тренияСкачать

Уравнение Навье — Стокса для вязких жидкостей

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье — Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье — Стокса и закон Ньютона совпадают).

Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье — Стокса, т.е. являются ньютоновскими жидкостями.

Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера — это частный (предельный) случай больших скоростей гидродинамики Навье — Стокса.

При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).

Видео:Первый, второй, третий закон Ньютона. 10 класс.Скачать

Критерий Рейнольдса

Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 — 1912).

Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.

Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:

Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:

Работа этой силы при перемещении элемента жидкости на расстояние n составляет

а отношение кинетической энергии элемента жидкости к работе силы трения равно

Сокращаем и получаем:

Re — называется числом Рейнольдса.

Таким образом, Re — это безразмерная величина, которая характеризует относительную роль сил вязкости.

Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.

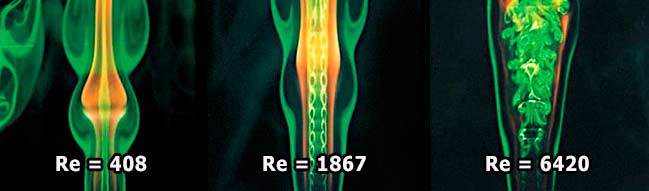
Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina — «пластинка») течение превращается в турбулентное (от латинского turbulentus — «бурный», «беспорядочный»), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.

Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен — охлаждение или нагревание агрегатов — происходит существенно интенсивнее; быстрее идёт распространение химических реакций.

Формула Бернулли закон по которому течет жидкость на любом отрезке трубы, что значительно помогает при проектировании трубопроводов, особенно с естественной циркуляцией.

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Видео:Урок 39 (осн). Сила трения. Коэффициент тренияСкачать

Вязкость жидкости. Закон Ньютона. Ньютоновские и неньютоновские жидкости.

Основные величины, характеризующие движение жидкости или газа. Линейная и объёмная скорости; соотношение между ними.

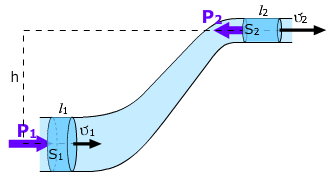
Основной характеристикой любого движения является его скорость. В случае течения жидкости (или газа) термин „скорость“ применяется в двух смыслах. Скорость перемещения самих частиц жидкости(или плывущих вместе с жидкостью мелких тел – например, эритроцитов в крови)обозначают υ и называют линейной скоростью. м/с , где х – координата частицы (при равномерном движении можно написать ). Однако, на практике чаще важнее знать объём V жидкости, протекающей в данном потоке(в трубе, в русле реки, в кровеносном сосуде и т.п.) за единицу времени.Эту величину называют объёмной скоростью и обозначают Q.

Q = . (1)

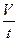
Между линейной скоростью υ и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S (см. рисунок 1).

Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1. Через некоторое время t он переместится в положение 2, отстоящее на расстояние x = υ·t . При этом через трубку пройдёт объём жидкости V = S·x . Объёмная скорость жидкости Q при этом будет равна 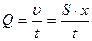. Но , поэтому

Если течение стационарно, то

Это уравнение неразрывности струи.

Течение идеальной жидкости. Теорема Бернулли.

Идеальная жидкость – жидкость несжимаемая и неимеющая силы внутреннего трения. Следовательно при движении жидкости не происходит диссипации энергии, ее полная энергия постоянна. Если жидкость движется под действием внешнего давления, то ее полная энергия есть сумма кинетической энергии, потенциальной энергии ,силы тяжести и потенциальной энергии давления. . Для идеальной жидкости Е= const. . Разделим на объем жидкости V, так как жидкость несжимаема, V = const.

, — плотность жидкости.

уравнение (теорема) Бернулли.

р – внешнее статическое давление, которое, согласно закона Паскаля, передается жидкостью во все стороны без изменения. давление силы тяжести жидкости или гидростатическое давление. — давление, создаваемое вследствие движения жидкости -–динамическое давление, направленное по вектору скорости жидкости. Для горизонтального течения жидкости, когда =const, можно уравнение Бернулли упростить: .

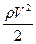
При нормальном кровообращении, как нетрудно подсчитать, динамическое давление составляет всего 1% 3% от полного. Например, в аорте линейная скорость крови около 0,7 метра в секунду, откуда

(плотность крови ≈ 1000 кг.м –3 ). Полное давление крови в аорте (среднее) около 120 мм.рт.столба. Учитывая, что 1 мм.рт.ст. = 133 паскаля, получаем, что полное давление равно 16.10 3 Па, то есть р_{динамич} ≈ 1,5%. Однако, при усиленной физической нагрузке, а также при некоторых заболеваниях динамическое давление заметно возрастает, и его необходимо учитывать.

Вязкость жидкости. Закон Ньютона. Ньютоновские и неньютоновские жидкости.

В реальных жидкостях всегда существуют силы трения. Причины трения – межмолекулярные взимодействия. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трениемили вязкостью (эти термины являются синонимами).

Рассмотрим два слоя жидкости, движущиеся с разными скоростями (рис. 5). Расстояние между слоями равно х.

S

SSs v ₁

Х S v ₂

Выделим в каждом слое площадку с площадью S. Ньютон показал, что сила трения между этими слоями равна:

(6)

(знак „минус“ показывает, что сила трения направлена навстречу движению). Эта формула носит название формула Ньютона.

Коэффициент η (эта) называется коэффициент вязкости или просто вязкость (реже говорят „коэффициент внутреннеготрения“). F = — η grad S Размерность величины η есть Па.с;

Ньютоновские и неньютоновские жидкости

Для большинства жидкостей коэффициент вязкости η при постоянной температуре есть постоянная величина, зависящая только от природы жидкости и не зависящая от её скорости (точнее, от градиента скорости; см. формулу «8»). Такие жидкости принято называть „ньютоновскими“, то есть строго подчиняющимися закону Ньютона.

Однако, опыт показал, что для ряда жидкостей η ≠ const. При малых градиентах скорости(что чаще всего бывает, когда сама скорость движения жидкости мала) вязкость относительно велика, но с ростом градиента скорости вязкость уменьшается,приближаясь к некоторому, сравнительно малому постоянному значению η_0.

Такие жидкости называются „неньютоновскими“ К ним относятся, во-первых, растворы веществ, молекулы которых в растворе образуют достаточно сильные межмолекулярные связи. Эти связи затрудняют перескоки молекул из одного положения в другое и тем самым снижают текучесть раствора, то есть увеличивают его вязкость. Плазма крови содержит большое количество растворённых белков, и в ней плавает большое число клеток (в основном – эритроцитов); кровь – это типичная неньютоновская жидкость. Поэтому, в частности, в капиллярах, где скорость течения крови мала, вязкость крови заметно больше, чем в крупных сосудах; это необходимо учитывать при расчётах движения крови в системе кровообращения.

📺 Видео

Первый закон НьютонаСкачать

Третий закон НьютонаСкачать

Физика - первый и второй законы НьютонаСкачать

Второй закон НьютонаСкачать

14408 Применение законов Ньютона.Вязкое трениеСкачать

СИЛА ТРЕНИЯ | коэффициент трения | ДИНАМИКАСкачать

Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Физика - третий закон НьютонаСкачать

Применение II закона Ньютона. Разбор на примерахСкачать