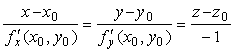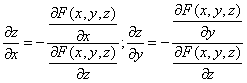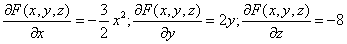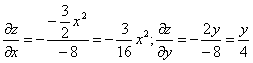Уравнение нормали к поверхности параллельной прямой

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Математический анализ
• Касательная плоскость и нормаль к явно заданной поверхности.

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Касательная плоскость и нормаль к явно заданной поверхности.

Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.

Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac=frac=frac.$$

Примеры:

7.229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=sin xcos y$ в точке $(pi/4, pi/4, pi/4).$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac=frac=frac.$$

Находим частные производные:

$z’_x=(sin xcos y)’_x=cos xcos y;$

$z’_y=(sin xcos y)’_y=-sin xsin y;$

Таким образом, уравнение касательной плоскости: $$z-frac=frac(x-frac)-frac(y-frac)Rightarrow$$ $$fracx -fracy-z+frac=0.$$

7.232. Для поверхности $z=4x-xy+y^2$ найти уравнение касательной плоскости, параллельной плоскости $4x+y+2z+9=0.$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0).$$

Находим частные производные:

Отсюда находим уравнение касательной плоскости: $$z-z_0=(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)Rightarrow$$ $$(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)-z+z_0=0.$$

Найдем точку поверхности $M(x_0, y_0, x_0)$ касательная плоскость к которой будет параллельна плоскости $4x+y+2z+9=0:$

Таким образом, уравнение касательной плоскости: $$z-11=(4-6)(x-frac)+(-frac+2cdot 6)(y-6)Rightarrow$$ $$z-11=-2(x-frac)-frac(y-6)Rightarrow 2x+fracy+z-11-25-3=0Rightarrow$$ $$Rightarrow4x+y+2z-78=0.$$

7.233. а) Найти уравнения касательной плоскости и нормали к поверхности $x(y+z)(xy-z)+8=0$ в точке $(2, 1, 3).$

Решение.

Для поверхности $$F(x,y,z)=0,$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

$F(x, y, z)=x(y+z)(xy-z)+8=x^2y^2-xyz+x^2yz-xz^2+8=0$

Находим частные производные:

Отсюда находим уравнение касательной плоскости: $$4(x-2)+14(y-1)-10(z-3)=0Rightarrow 4x+14y-10z+8.$$

Домашнее задание.

7.229. б) Найти уравнения касательной плоскости и нормали к поверхности $z=e^$ в точке $(1, pi/ 1/e).$

7.230. Найти расстояние от начала координат до касательной плоскости к поверхности $z=y tgfrac$ в точке $left(fracright).$

7.233. б) Найти уравнения касательной плоскости и нормали к поверхности $2^+2^=8$ в точке $(2, 2, 1).$

7.234. Для поверхности $x^2-z^2-2x+6y=4$ найти уравнение нормали, параллельной прямой $frac=frac=frac.$

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение нормали к поверхности параллельной прямой

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Поверхности. Касательная плоскость и нормаль

Видео:Уравнение касательной, параллельной заданной прямой.Скачать

Краткие теоретические сведения

Способы задания поверхностей

Рассматриваем вектор–функцию двух скалярных аргументов: $$vec =vec (u,v).$$ Годографом такой функции является поверхность.

Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec =vec (u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$

Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.

Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.

Кривая, лежащая на поверхности $vec =vec (u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox $, $v=mbox $ являются координатными линиями данной параметризации поверхности.

Видео:Уравнение параллельной прямойСкачать

Решение задач

Задача 1 (Феденко №544)

Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.

Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.

Задача 2 (Феденко № 546)

Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox ,u,mbox ,v, \ y & = y_0 + b,mbox ,u,mbox ,v, \ z & = z_0 + c,mbox ,u. end end

Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac +frac +frac =1. end

Задача 3 (Феденко №528)

В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.

Решение задачи 3

Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left x_0 & = & f(u_0),mbox ,v, \ y_0 & = & f(u_0),mbox ,v, \ z_0 & = & g(u_0). \ end right. end

Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left x & = & f(u),mbox ,v, \ y & = & f(u),mbox ,v, \ z & = & g(u). \ end right. end

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Касательная плоскость. Нормаль

Видео:Уравнение плоскости через точку и нормальСкачать

Краткие теоретические сведения

Пусть $vec =vec (u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.

Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec =vec (u,v)$ определяется вектором: begin displaystylefrac >

=vec _udisplaystylefrac +vec _vdisplaystylefrac , end где $vec _u=displaystylefrac > $, $vec _v=displaystylefrac > $. Для разных кривых, проходящих через точку $P(u_0, v_0)$, значения $displaystylefrac $, $displaystylefrac $ будут разными, а $vec _u$, $vec _v$ теми же. Следовательно, все векторы $displaystylefrac > $ лежат в одной плоскости, определяемой векторами $vec _u$, $vec _v$. Эта плоскость называется касательной плоскостью к поверхности в точке $P$. Запишем уравнение касательной плоскости.

Обозначения:
— $vec = $ — радиус-вектор произвольной точки касательной плоскости.
— $vec = $ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.

Уравнение касательной плоскости:

1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec -vec , , vec _u, , vec _v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end

Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.

Уравнение нормали:

Видео:7. ФНП. Касательная плоскость и нормальная прямая к поверхностиСкачать

Решение задач

Задача 1 (Феденко №574)

Дана поверхность begin x=u,mbox ,v,,, y=u,mbox ,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefrac right)$ поверхности.

Задача 2

Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec = $.

Ответ. $z=0, -2X-2Y+Z+2=0$.

Задача 3

Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec $.

Задача 4

Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.

Ответ. $X-Z=0$, $3X-4Y+5Z=0$.

Задача 5 (Феденко №594)

Докажите, что поверхности begin z=mbox (xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.

Решение задачи 5

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Математический портал

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Математический анализ
• Касательная плоскость и нормаль к явно заданной поверхности.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Касательная плоскость и нормаль к явно заданной поверхности.

Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.

Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac =frac =frac .$$

Примеры:

7.229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=sin xcos y$ в точке $(pi/4, pi/4, pi/4).$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac =frac =frac .$$

Находим частные производные:

$z’_x=(sin xcos y)’_x=cos xcos y;$

$z’_y=(sin xcos y)’_y=-sin xsin y;$

Таким образом, уравнение касательной плоскости: $$z-frac =frac (x-frac )-frac (y-frac )Rightarrow$$ $$frac x -frac y-z+frac =0.$$

7.232. Для поверхности $z=4x-xy+y^2$ найти уравнение касательной плоскости, параллельной плоскости $4x+y+2z+9=0.$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0).$$

Находим частные производные:

Отсюда находим уравнение касательной плоскости: $$z-z_0=(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)Rightarrow$$ $$(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)-z+z_0=0.$$

Найдем точку поверхности $M(x_0, y_0, x_0)$ касательная плоскость к которой будет параллельна плоскости $4x+y+2z+9=0:$

Таким образом, уравнение касательной плоскости: $$z-11=(4-6)(x-frac )+(-frac +2cdot 6)(y-6)Rightarrow$$ $$z-11=-2(x-frac )-frac (y-6)Rightarrow 2x+frac y+z-11-25-3=0Rightarrow$$ $$Rightarrow4x+y+2z-78=0.$$

7.233. а) Найти уравнения касательной плоскости и нормали к поверхности $x(y+z)(xy-z)+8=0$ в точке $(2, 1, 3).$

Решение.

Для поверхности $$F(x,y,z)=0,$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

$F(x, y, z)=x(y+z)(xy-z)+8=x^2y^2-xyz+x^2yz-xz^2+8=0$

Находим частные производные:

Отсюда находим уравнение касательной плоскости: $$4(x-2)+14(y-1)-10(z-3)=0Rightarrow 4x+14y-10z+8.$$

Домашнее задание.

7.229. б) Найти уравнения касательной плоскости и нормали к поверхности $z=e^ $ в точке $(1, pi/ 1/e).$

7.230. Найти расстояние от начала координат до касательной плоскости к поверхности $z=y tgfrac $ в точке $left(frac right).$

7.233. б) Найти уравнения касательной плоскости и нормали к поверхности $2^ +2^ =8$ в точке $(2, 2, 1).$

7.234. Для поверхности $x^2-z^2-2x+6y=4$ найти уравнение нормали, параллельной прямой $frac =frac =frac .$

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

📽️ Видео

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Репетитор по математике ищет нормаль к плоскостиСкачать