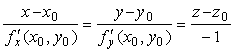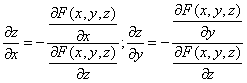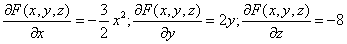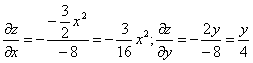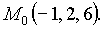Уравнение нормали к графику функции двух переменных

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Видео:УРАВНЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХСкачать

Экстремум функции двух переменных. Касательная плоскость и нормаль к поверхности

Касательная плоскость и нормаль к поверхности. Экстремум функции двух переменных

ПЛАН

Касательная плоскость и нормаль к поверхности.

Экстремум функции двух переменных.

Необходимые и достаточные условия существования

экстремума функции z = f(х, у).

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности S в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности S через точку М₀.

Уравнение касательной плоскости к поверхности, заданной равнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Вектор называется вектором нормали к поверхности S в точке М₀. Вектор нормали перпендикулярен касательной плоскости.

Нормалью к поверхности S в точке М₀ называется прямая, проходящая через эту точку и имеющая направление вектора N. Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀), где z₀ = f(x₀,y₀), имеют вид:

(2)

Пусть поверхность задана уравнением

(3)

в неявном виде. Будем считать, что и в некоторой окрестности точки функция имеет непрерывные частные производные, одновременно не равные нулю. Тогда

(4)

Условимся писать вместо .

Уравнение касательной плоскости к в точке запишется так:

, (5)

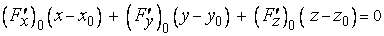
а уравнение нормали к в точке — так:

. (6)

Пример 1. Уравнение

(7)

определяет круговой конус с вершиной в начале координат и осью, совпадающей с осью (рис. 1).

Левая часть уравнения (7) имеет частные производные

,

одновременно не равные нулю, если точка 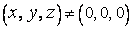. В любой такой точке, которую обозначим через , касательная плоскость определяется уравнением

.

Нормаль к в точке , т. е. прямая, проходящая через эту точку, перепендикулярно к касательной плоскости, очевидно, имеет уравнение

.

Пример 2. Найти уравнение касательной плоскости и уравнение нормали к поверхности

в точке

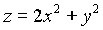
Решение: Имеем

Тогда, согласно (1), уравнение касательной плоскости к данной поверхности в указанной точке будет иметь вид: z — 6 = — 4(x + 1) + 2(y — 2), то есть

4x — 2y + z + 2 = 0, а уравнение нормали, согласно (2):

Пример 3. Найти уравнение касательной плоскости и нормали к конусу

Решение. Имеем

Уравнение касательной плоскости запишем в виде

или .

Уравнение нормали имеет вид

Экстремум функции двух переменных

Пусть функция z = f(х, у) определена в некоторой области D и точка М₀(х₀, у₀) ÎD (внутренняя точка области).

Определение. Точка М₀(х₀, у₀) называется точкой максимума(минимума) функции z = f(х, у), если в достаточно малой d-окрестности точки М₀ для каждой точки М(х, у) отличной от точки М₀(х₀, у₀), выполняется неравенство:

На рис.1 М₀ – точка максимума, а

точка М₁ – точка минимума функ-

ции z = f(х, у).

Значение функции в точке макси-

мума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции

называется её экстремумом.

Замечание. Согласно определению, точка экстремума функции является внутренней точкой области определения функции. Максимум и минимум имеют локальный (местный) характер: значения функции в точке М₀(х₀, у₀) сравниваются с её значениями в точках достаточно близких к М₀(х₀, у₀). В области D функция может иметь несколько экстремумов или не иметь ни одного.

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Касательная и нормаль к графику функции

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Основные формулы

Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной

Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓

Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓

Видео:Как составить уравнение касательной и нормали к графику функцииСкачать

Определения

Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.

Определение касательной приводится здесь. Уравнение касательной:
.

Касательная TM₀, нормаль M₀N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
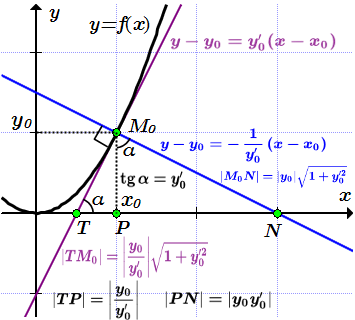
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Полезные формулы из аналитической геометрии

Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.

Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.

Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .

Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :

Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.

Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.

Уравнение прямой в отрезках, пересекающей оси координат в точках :
.

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Примеры решения задач

Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓

Пример 1

Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.

Находим значение функции при :
.

Находим производную:
.
Находим производную в точке :
;
.

Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .

Касательная и нормаль к графику функции y=x 2 в точке M₀(1;1).

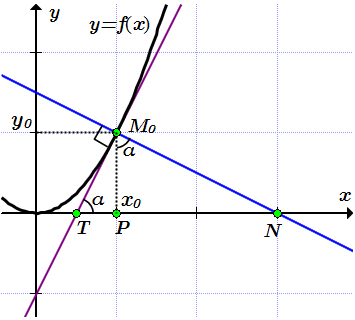
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.

Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .

Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.

Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка поднормали . Из прямоугольника имеем:
.

Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.

Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .

Пример 2

Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .

Находим значения переменных при .
;
.
Обозначим эту точку как .

Находим производные переменных x и y по параметру t .
;
;
;
;
.

Подставляя , находим производную y по x в точке .
.

Касательная и нормаль к циссоиде в точке (2;2).

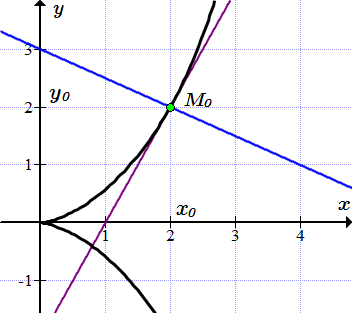
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.

Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.

Уравнение касательной: .
Уравнение нормали: .

Пример 3

Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .

Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.

Находим производную в заданной точке, подставляя .
;
.

Находим уравнение касательной по формуле (2).
;
;
;
.

Находим уравнение нормали по формуле (3).
;
;
;
.

Касательная и нормаль к циссоиде изображены на рисунке ⇑.

Уравнение касательной: .
Уравнение нормали: .

Пример 4

Найти угол между кривыми и .

Найдем множество точек пересечения кривых, решая систему уравнений.

Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .

Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.

Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Вывод формулы для угла между кривыми

Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .

Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .

Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.

В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .

На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .

При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.

1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).

2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:

.

Этот случай изображен на рисунке ⇑.

3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).

Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.

Автор: Олег Одинцов . Опубликовано: 30-06-2021

🎥 Видео

Уравнения касательной и нормали к графику функции (часть 1). Высшая математика.Скачать

Касательная к графику функции в точке. 10 класс.Скачать

Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Уравнение касательной и нормали к графику функцииСкачать

Уравнение касательнойСкачать

Уравнение нормали к кривой.Скачать

14.1. Касательная к параметрически заданной функцииСкачать

Уравнения касательной и нормали к кривойСкачать

Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Уравнения касательной плоскости и нормали к поверхностиСкачать

Геометрический смысл производной. Уравнение касательнойСкачать