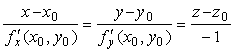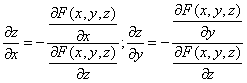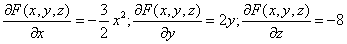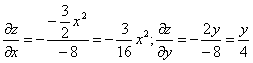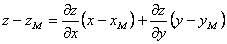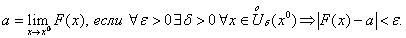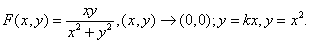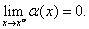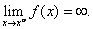Уравнение нормали функция трех переменных

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Примеры решений задач: функции нескольких переменных

В этом разделе вы найдете готовые задания разного типа для функций нескольких переменных:

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Примеры: область определения ФНП

Задача 1. Найти область определения функции двух переменных $z=f(x,y)$. Изобразить ее на координатной плоскости и заштриховать.

Задача 2. Для данной функции найти область определения и изобразить ее на рисунке в системе координат.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Примеры: частные производные ФНП

Задача 3. Найти частные производные: $z=tg^3 (3x-4y)$

Задача 4. Найти частные производные второго порядка $z=sqrt$

Задача 5. Найти частные производные сложной функции:

$$ z=u^2 cdot ln v; quad u=frac, , v=x^2+y^2.$$

Задача 6. Проверить справедливость теоремы о смешанных производных второго порядка.

Задача 7. Найти полный дифференциал данной функции

Задача 8. Найти дифференциал второго порядка функции:

Задача 9. Для функции $z(x,y)$ двух переменных, неявно заданной уравнением $sin(xz)+cos(yz)=1$, найдите первый и второй дифференциалы в точке $x=y=1, z=0$.

Задача 10. Проверить, удовлетворяет ли функция двух переменных $z(x,y)$ указанному дифференциальному уравнению.

Видео:Математический анализ, 29 урок, Функции нескольких переменных. Частные производныеСкачать

Градиент, производная по направлению

Задача 11. Найти производную функции $f(x,y,z)$ в точке $M(x_0,y_0,z_0)$ по направлению вектора $overline$. Вычислить наибольшую скорость изменения функции в данной точке.

Задача 13. Найдите градиент, производную по направлению $overline$ и матрицу Гессе в точке $M$ заданной функции, где $u=f(x,y,z)=x^2z+z^2x^2+y^3$, $overline=$, $M(1,3,1)$.

Задача 14. Найти производную функции $u$ в точке $M$ по направлению нормали к поверхности $S$, образующей острый угол с положительным направлением оси $Oz$.

Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Касательная плоскость и нормаль

Задача 15. Составить уравнения касательной плоскости и нормали к поверхности $x^2+y^2-x+2y+4z-13=0$ в точке $M(2,1,2)$.

Задача 16. Для кривой $overline=overline(t)$ найти в точке $t_0$ уравнение касательной, уравнение нормальной плоскости и вычислить кривизну линии.

$$ overline(t)=(t^2-3)overline + (t^3+2)overline+ln t overline, quad t_0=1 $$

Задача 17. Найти градиент, первый дифференциал, матрицу вторых производных, второй дифференциал функции $z=2xy-xy^4+5y^3-3$ в точке $A(2,-3)$. Составить уравнения касательной плоскости и соприкасающегося параболоида к графику данной функции.

Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Экстремумы функции нескольких переменных

Задача 18. Найти точки экстремума функции $z=x^2+xy+y^2+2x-y$.

Задача 19. Найти точки локального экстремума и экстремальные значения $z=x^2+y^2-xy+x+y$.

Задача 20. Исследовать на экстремум функцию $z=x^4+xy+fracy^2+5$.

Задача 21. Определите, при каких значениях параметра $a$ функция $z(x,y)=x^3+y^3+4xy-7x-7y+a(x-1)^2+a(y-1)^2$ в точке (1;1):
А) имеет максимум,
Б) имеет минимум,
В) не имеет экстремума.

Задача 22. Найдите (локальные) экстремумы функции трех переменных $f(x,y,z)=2x^2-xy+2xz-y+y^3+z^2$.

Видео:Функции нескольких переменных. Теория. Касательная плоскость и нормаль к поверхностиСкачать

Приближенные вычисления

Задача 23. Вычислить приближенно значение функции $Z=Z(x,y)$ и данной точке с помощью дифференциала.

Задача 24. Дана функция $z=x^2+2xy+3y^2$ и две точки $А (2; 1)$ и $В (1,96; 1,04)$. Требуется:
1) вычислить точное значение функции в точке $В$;
2) вычислить приближённое значение функции в точке $В$, исходя из значения функции в точке $А$ и заменив приращение функции при переходе от точки $А$ к точке $B$ дифференциалом;
3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Ряд Тэйлора

Задача 25. Разложите функцию $f(x,y)=x^2ln y + y^2$ по формуле Тейлора (с остаточным членом в форме Пеано) в окрестности точки $M(2;1)$ до членов второго порядка включительно. Выпишите первый и второй дифференциалы заданной функции.

Задача 26. Найти первые и вторые частные производные функции $F$ и записать формулу Тэйлора в указанной точке $x^0$.

Видео:УРАВНЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХСкачать

Наибольшее и наименьшее значение в области

Задача 27. Найти наименьшее $m$ и наибольшее $M$ значения функции $z=f(x,y)=3-2x^2-xy-y^2$ в замкнутой области $D$, заданной системой неравенств $-1 le x le 1; 0le y le 2$. Сделать чертёж области $D$.

Задача 28. Экстремумы функций нескольких переменных. Требуется найти наибольшее и наименьшее значения функции $z=5x^2-3xy+y^2+4$ в области, ограниченной заданными линиями $x=0, y=0, x+y=2$.

Видео:Уравнения касательной плоскости и нормали к поверхностиСкачать

Решение контрольной

Контрольное задание. Дана функция $f(x,y)=x^2+y^2-3xy$
1. Исследовать функцию $f$ на экстремум. Найти экстремальные значения функции.
2. Найти наибольшее и наименьшее значения функции $f$ в заданной области $D$.
3. Составить уравнение касательной плоскости к поверхности $z=f(x,y)$ в точке, где $x=x_0=1$, $y=y)0=3$.
4. Найти величину наибольшей скорости возрастания функции $f$ в точке $M_1(-1;1)$.
5. Вычислить производную функции $f$ в точке $M_1$ в направлении вектора $overline$. Каков характер изменения функции? Почему?
6. Найти угол между градиентами функции $f$ в точках $M_1$ и $M_2(2;2)$. Построить векторы и указать угол.

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Видео:7. ФНП. Касательная плоскость и нормальная прямая к поверхностиСкачать

Производная по направлению. Градиент. Уравнение касательной плоскости к поверхности. Уравнение нормали

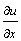
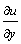
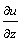
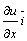
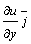
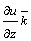
Вектор с координатами , , называется градиентом функции u = f (x, y, z) в точке M(x, y, z) и обозначается grad u = + + .

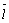
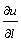
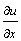
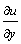
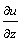
Под производной функции u = f (x, y, z) в данном направлении понимается выражение = cosa + cosb + cosg, где cosa, cosb, cosg – направляющие косинусы вектора

Производная 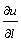представляет собой скорость изменения функции в данном направлении.

Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).

Как известно, проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению.

Градиент функции в данной точке указывает напрвление наиболее быстрого возрастания функции.

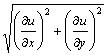
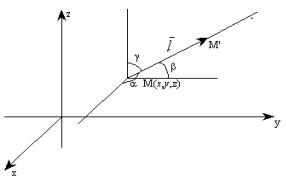
Величина градиента, т.е. | grad u | = обозначается tg j и определяет крутизну наибольшего ската или подъема поверхности u = f (x, y).

Пусть М – точка поверхности S. Плоскость, содержащая точку М и обладающая тем свойством, что расстояние от этой плоскости до переменной точки M₁ поверхности S является бесконечно малым по сравнению с расстоянием ММ₁, называется касательной плоскостью к поверхности S в точке М.
Если поверхность в трехмерном пространстве задана уравнением f(x; y; z) = 0, где функция f достаточное число раз дифференцируема, то уравнение плоскости, касательной к этой поверхности в точке М(х_М; у_М; z_М), имеет вид:

, (**)

где 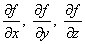– частные производные функции трех переменных f(x; y; z) по этим переменным.
Если же поверхность задана уравнением, разрешенным относительно аппликаты z, т.е. имеет вид z = z(x; y), то уравнение (**) касательной плоскости принимает вид:

(конечно, предполагается, что функция z имеет непрерывные первые частные производные).

Нормаль (франц. normal, от лат. normalis — прямой) к кривой (к поверхности) в данной её точке — прямая, проходящая через эту точку и перпендикулярная к касательной

прямой (касательной плоскости) в этой же точке кривой (поверхности). Плоская кривая имеет в каждой точке единственную Нормаль, расположенную в плоскости кривой. Если х = f (t) и у = g (t) — параметрические уравнения плоской кривой L, то уравнение Нормаль в точке (x₀, y₀) кривой L, соответствующей значению t₀ параметра t, может быть записано в виде:

.

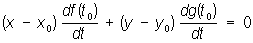
Для плоской кривой, заданной уравнением F (х, у) = 0, уравнение Нормаль имеет вид:

.

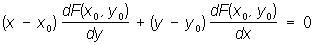
Пространственная кривая имеет в каждой своей точке бесчисленное множество Нормаль, заполняющих некоторую плоскость (нормальную плоскость). Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Нормаль, перпендикулярную к соприкасающейся плоскости, называется бинормалью. Касательная, главная Нормаль и бинормаль образуют подвижный триэдр кривой.

Для поверхности, заданной уравнением F (х, у, z) = 0, Нормаль может быть представлена уравнениями:

.

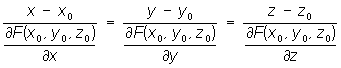
Понятие Нормаль играет существенную роль не только в дифференциальной геометрии, но и в различных её приложениях: в геометрической оптике (например, в формулировке основных законов преломления и отражения световых лучей), в механике (материальная точка или тело при перемещениях по гладким линиям или поверхностям испытывают реакцию, направленную по Нормаль, в консервативном поле силовые линии в каждой точке имеют направление Нормаль к изопотенциальной поверхности, проходящей через эту точку, и т.д.).

58. Екстремум функції двох змінних.

Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной (см. п. 25.4).

Пусть функция z = ƒ(х;у) определена в некоторой области D, точка N(x₀;y₀) Î D.

Точка (х₀;у₀) называется точкой максимума функции z=ƒ(х;у), если существует такая d-окрестность точки (х₀;у₀), что для каждой точки (х;у), отличной от (х_о;у_о), из этой окрестности выполняется неравенство ƒ(х;у) ƒ(х₀;у₀).

На рисунке 210: N₁ — точка максимума, а N₂ — точка минимума функции z=ƒ(x;у).

Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами.

Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (х₀;у₀) сравнивается с ее значениями в точках, достаточно близких к (х₀; у₀). В области D функция может иметь несколько экстремумов или не иметь ни одного.

59. Найбільше та найменше значення функції багатьох змінних у замкненій області.

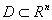
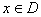
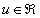
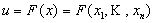
Рассматривается множество . Если определено правило, по которому каждой точке ставится в соответствие некоторое число (единственным образом), то говорят, что на множестве D определена (однозначная) функция . Как обычно, множество D называется областью определения функции, а множество всех соответствующих значений u: Q = <u> – множеством значений. Часто функцию u = F(x) называют отображением

При n = 2 уравнение F(x,y) = C задает линии уровня поверхности z = F(x,y), а при n = 3 уравнение F(x,y,z) = С – поверхности уровня.

Задание ФНП может быть неявным: F(x,u) = 0 или параметрическим .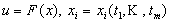

Примеры .Поверхности 2 – го порядка.

Как и в случае одной переменной, определяется предел ФНП:

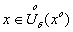
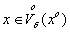
Вместо условия можно писать .

Справедливы все общие свойства пределов: арифметические свойства, переход к пределу в неравенствах и т.д.

Тем не менее, понятие предела ФНП оказывается более сложным за счет того, что стремление т. х к х о может осуществляться большим числом способов, нежели в случае одной переменной.

Пример.

По аналогии с функциями одной переменной, вводятся бесконечно малые и большие величины и понятие непрерывности:

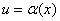
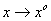
Функция называется бесконечно малой при , если

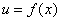
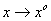
Функция называется бесконечно большой при , если

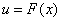
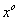
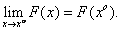
Функция называется непрерывной в т. , если Функция непрерывна на множестве, если она непрерывна в каждой точке этого множества.

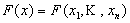
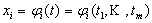
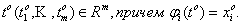
Остаются верными все свойства непрерывных функций: арифметические свойства, теорема о сохранении знака. Теоремы об ограниченности непрерывной функции, о переходе через промежуточные значения и о достижении максимума и минимума формулируются для замкнутых областей. Верна также теорема о непрерывности сложной функции: пусть функция непрерывна в т. х о , а функции в т. В этом случае функция

🎦 Видео

Касательная и нормаль к поверхностиСкачать

Частные производные функции многих переменныхСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Касательная плоскость и нормаль к поверхности | ФНП 2.4Скачать

14.1. Касательная к параметрически заданной функцииСкачать

Экстремум функции двух/трех переменных, задачиСкачать

Нахождение уравнения касательной плоскости и уравнения нормалиСкачать