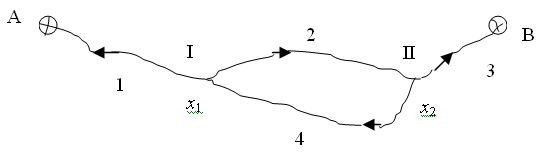
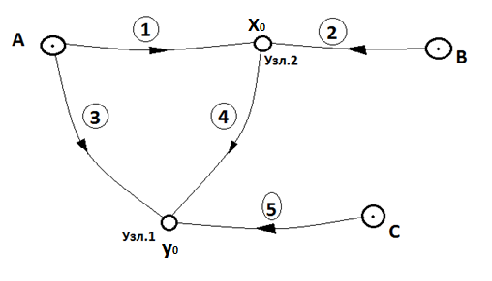
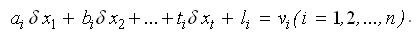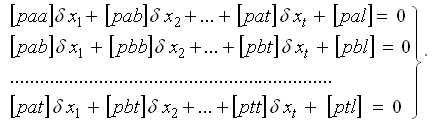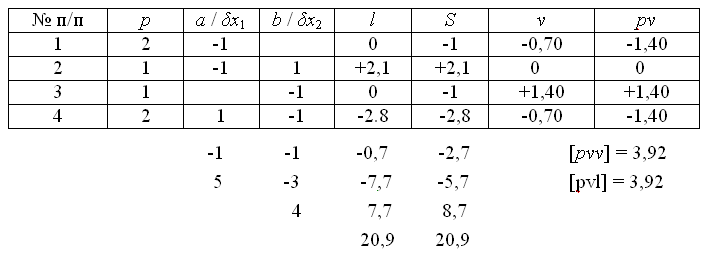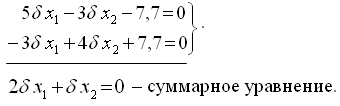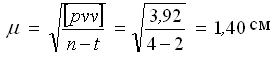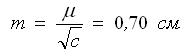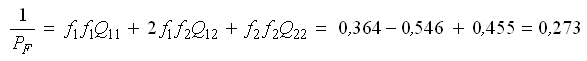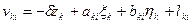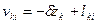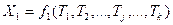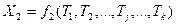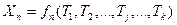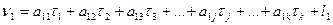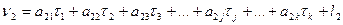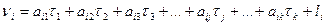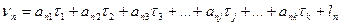Рис. 3. Нивелирная сеть
НА = 100,000 м; НВ = 115,000 м — отметки исходных пунктов.
h (м): 5,023; 10,012; 9,990; -10,005 — измеренные превышения.
S (км): 2; 4; 4; 2 — длины ходов.
pi = c/Si: 2; 1; 1; 2 — веса результатов измерений (с = 4 ).
В данной нивелирной сети число измерений n = 4, число необходимых измерений t = 2. Два параметра х1 и х2 — отметки вновь определяемых пунктов.
Параметрические уравнения связи составим по формуле:
— параметрические уравнения связи.
Определим приближенные значения параметров:
x1 = х 0 1 + δх1 и x2 = x 0 2 + δx2 подставим в систему параметрических уравнений связи.
Переходим к параметрическим уравнениям поправок:
Свободные члены li = Fi(x1 0 , x2 0 , . xt 0 ) — yi, (i = 1, 2, . n) выразим в сантиметрах или в миллиметрах для того, чтобы порядок коэффициентов и свободных членов был одинаков.
Переходим к системе нормальных уравнений:
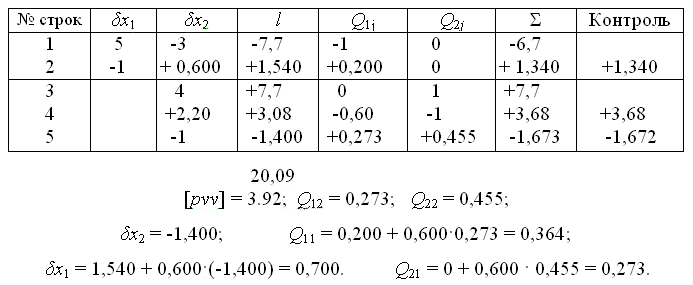
Коэффициенты и свободные члены параметрических уравнений поправок поместим в табл. 10.
Таблица параметрических уравнений поправок
Система нормальных уравнений имеет вид:
Решение системы нормальных уравнений с определением элементов обратной матрицы выполним в схеме Гаусса (табл. 10).
Решение нормальных уравнений
Контроль δхj: Контроль Qij: 2 · 0,364 + 0,273 — 1 = 0,001;
2 · 0,700 — 1,400 = 0. 2 · 0,273 + 0,455 — 1 = 0,001.
Вычислим значение параметров:
Вычислим уравненные результаты измерений, делаем контроль уравнивания (табл. 12).
Уравненные превышения. Контроль уравнивания
| № п/п | hi + vi | F(x1, x2) | № п/п | hi + vi | F(x1, x2) |
| 5,0160 | НА — х1 | 5,0160 | 10,0040 | НВ — х2 | 10,0040 |
| 10,0120 | х2 — х1 | 10,0120 | -10,0120 | х1 — х2 | -10,0120 |
Сделаем оценку точности результатов измерений по материалам уравнивания:
— средняя квадратическая ошибка единицы веса (превышения по ходу в 4 км).
— средняя квадратическая ошибка на 1 км хода.
Оценку точности параметров и функции параметров выполним с использованием элементов обратной матрицы
по формулам (38) и (37):
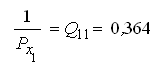
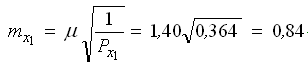
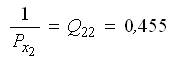
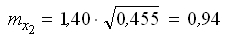

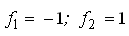
— обратный вес функции.
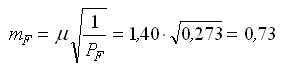
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Параметрический способ уравнивания
При уравнивании сложных по построению геодезических сетей, в которых имеется обычно большое число избыточных измерений, применение коррелатного способа является практически менее выгодным. Это связано с тем, что в сложных сетях образуется сравнительно большое число геометрических условий (см. § 134), т.е. возникает необходимость решения значительного числа нормальных уравнений. При уравнивании сложных геодезических сетей предпочтение отдают параметрическому способу. В данном случае его рекомендуется применять практически для любых построений: обширных геодезических сетей триангуляции и трилатерации, для весьма сложных фигур триангуляции 3 и 4 классов, в схемах различных линейно-угловых построений и др.
Чаще всего при уравнивании плановых геодезических построений параметрическим способом в качестве неизвестных величин (или необходимых параметров tj ) выбирают координаты определяемых пунктов, для которых из предварительных вычислений находят приближённые значения tj o , а затем определяют поправки τj к этим приближённым значениям. В качестве уравниваемых величин в плановых построениях принимают измеренные направления, углы, дирекционные углы (азимуты), длины сторон сетей. Промежуточными уравниваемыми величинами (как косвенными величинами) могут явиться и приращения координат точек планового построения.
Для нахождения поправок при уравнивании параметрическим способом необходимо составить параметрические уравнения связи, которые в полной мере обеспечат решение поставленной задачи. Все измеренные величины практически можно выразить через координаты точек сети, т.е. через выбранные параметры tj, что и требуется при уравнивании параметрическим способом. Так, дирекционные углы α и длины s сторон можно найти по разностям координат, горизонтальные углы, в свою очередь, выразить через разность дирекционных углов и т.п.
Рассмотрим различные виды уравнений поправок, применяемых при уравнивании параметрическим способом.
Уравнение поправок для измеренного дирекционного угла находится из параметрического уравнения связи между дирекционным углом и координатами точек данной линии:
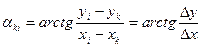
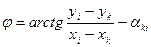
Известно, что 
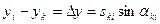
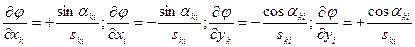
Свободный член lki уравнения поправок может быть найден из уравнения
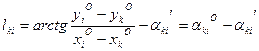
где х о и у о – значения искомых координат точек i и k , полученные по результатам предварительных вычислений по измеренным величинам; αki o и αki‘ – соответственно вычисленное и измеренное значение дирекционного угла. (Вычисленные значения необходимо давать с тем же порядком точности (округления), что и непосредственно измеренные величины).
Параметрическое уравнение поправок для измеренного дирекционного угла имеет вид:
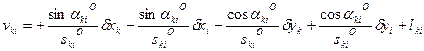
Выразим поправки 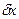


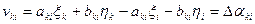
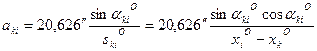
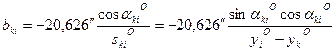
называются коэффициентами параметрического уравнения поправок.
При этом необходимо учитывать, что величины vki являются поправками для измеренных углов αki , а величины Δαki — поправками для вычисленных дирекционных углов αki o .
Уравнение поправок для измеренного направления может быть получено из следующего параметрического уравнения связи:
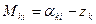
где Мki – измеренное направление; zk – ориентирующий (дирекционный) угол начального направления в точке k.
Выразим значение αki через выбранные параметры (14.105) и запишем параметрическое уравнение связи (14.113) в виде
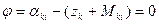
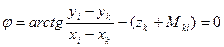
Если при предварительных вычислениях значение ориентирующего угла zk o определено с погрешностью δzk , то для любого направления на данном пункте существует постоянная погрешность величиной δzk.
Параметрическое уравнение поправок для измеренного направления Mki будет иметь вид:
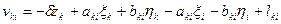
похожий на уравнение (14.110). Если дирекционный (ориентирующий) угол в исходном пункте получен без погрешности (т.е. погрешность его определения весьма мала по сравнению с погрешностями измерений других величин), то в выражении (14.116) можно исключить δzk .
Свободный член уравнения поправок в направления находят по формуле
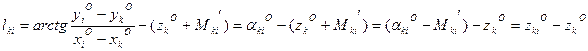
где αki о — точное значение дирекционного угла, вычисленное по координатам точек (предварительным их значениям); Mki‘ — измеренное значение направления; zki o — частные значения ориентирующего угла на пункте k ; zk o — предварительное значение дирекционного (ориентирующего) угла находят как среднее арифметическое из его частных значений:

В (14.118) n – число измеренных направлений на пункте k .
Отметим некоторые особенности уравнивания направлений на пункте k:
1. Сумма свободных членов на пункте должна быть равна нулю.
2. Из-за возможных погрешностей в вычислениях расстояния между пунктами следует определять дважды:
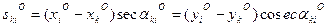
3. Сумма поправок в направления на каждом пункте должна быть равна нулю.
4. Уравнения поправок для прямого и обратного направлений различаются только значениями δz и свободными членами.
5. Если а) – пункт i исходный, а пункт k определяемый, либо б) – пункт i определяемый, а пункт k исходный, либо в) – оба пункта исходные, то уравнения поправок в направления имеют соответственно следующий вид:
а)
б) 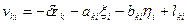
в)
6. Порядок уравнивания направлений в триангуляции параметрическим способом следующий (в качестве измеренных величин обычно берут направления):
— вычисляют предварительные значения координат и дирекционных углов;
— составляют параметрические уравнения связи, вычисляют коэффициенты и свободные члены уравнений поправок; составляют уравнения поправок для направлений, измеренных на пункте;
— составляют и решают нормальные уравнения поправок к предварительно вычисленным координатам;
— вычисляют окончательные значения координат пунктов;
— вычисляют поправки в измеренные направления;
— выполняют контроль обработки и оценивают точность уравненных величин (элементов сети).
Уравнение поправок для угла может быть получено на основании того, что значение угла равно разности дирекционных углов двух направлений:
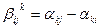
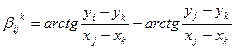
С учетом (14.116) можно записать, что
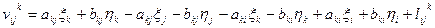
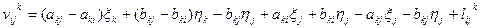
Вычисление свободных членов lij k контролируют невязками W треугольников:
вычисляют из предварительных определений дирекционных углов и значениям измеренных горизонтальных углов β.
Уравнение поправок для измеренного расстояния находят из параметрического уравнения связи
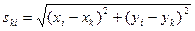
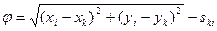
Если продифференцировать функцию (14.128) по переменным х и у, то получим частные производные
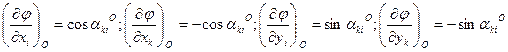
В этом случае параметрические уравнения поправок для измеренного расстояния будут иметь вид:
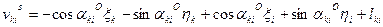
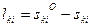
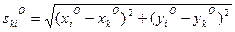
определяют по значениям координат х о и у о , полученных из предварительных вычислений, а ski — измеренное значение расстояния.
В уравнении поправок (14.130) все линейные величины должны быть выражены в одних и тех же единицах.
Как было сказано выше, решение задачи уравнивания параметрическим способом основано на представлении всех измеренных величин в виде функций некоторых выбранных параметров. Пусть, например, в треугольнике из n искомых элементов измерено k необходимых величин. В данном случае все избыточные элементы r можно выразить в виде их функций, т.е. здесь не возникает задачи уравнивания. Например, в треугольнике АВС измерены углы А и В и длина линии АВ = с. Остальные элементы можно найти из соотношений:
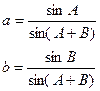
Если же измерены избыточные (r ) параметры С, а и b либо один из них, то возникает задача уравнивания.
Обозначим необходимые элементы буквой Тj. Для указанного треугольника в этом случае имеем: А = Т1, В = Т2, с = Т3. Соотношения (14.133) здесь можно записать в виде:
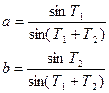
Пусть, как и в коррелатном способе уравнивания, истинные значения Х1, Х2, …, Хn (нам неизвестные) измерены, в результате чего получены значения х1, х2, …, хn , из которых k – необходимые, а r =( n – k) – избыточные. Значения xi получены с весами pi .
Выберем такие независимые между собой параметры Тj (j = 1, 2, …, k), функциями которых можно выразить все измеренные величины xi (i = 1, 2,…, n) Очевидно, что число таких параметров должно быть равно k необходимых измерений. Получим функции
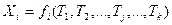
Равенства (14.135) называют параметрическими уравнениями связи.
Поскольку истинные значения Тj бывают неизвестными, то в процессе уравнивания получают их вероятнейшие значения, а затем находят уравненные значения всех измеренных величин.
Обозначим уравненные значения параметров Tj буквой tj , тогда
Из (14.136) следует, что
Если уравнения (14.136) имеют нелинейный вид, то решение этой системы уравнений практически невозможно.
Для решения системы уравнений (14.136) для параметров tj находят такие значения tj о (с такой их точностью), чтобы равенства (14.136) можно было привести к линейному виду разложением в ряд Тейлора с ограничением только членами первого порядка.
Для значений tj можно записать, что
где τj – поправки в приближенные значения параметров tj о . Тогда
Разложим функцию (14.139) в ряд Тейлора, ограничиваясь первыми членами разложения:
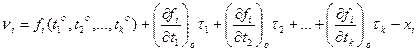
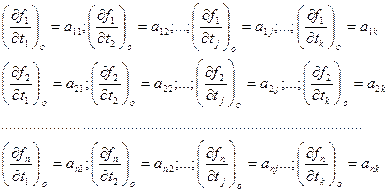
Первый индекс при параметре а показывает номер параметрического уравнения связи (измеренной величины), а второй – номер параметра t (и поправки τ. В общем виде
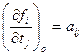
Найдём разности между вычисленными значениями xi o через приближённые значения параметров ti o и измеренными значениями xi . Эти разности li называются свободными членами параметрических уравнений поправок:
C учётом (14.143) систему уравнений (14.139) можно записать в развёрнутом виде:

В системе n уравнений (14.144) содержится (n+k) неизвестных, в связи с чем эта система является неопределённой. Так же, как и в коррелатном способе уравнивания, решение данной системы определяется условием минимума сумм квадратов поправок, т.е. [pv 2 ] = min.
Опуская промежуточные математические преобразования (о них можно посмотреть в соответствующей геодезической литературе), приведём окончательный вид системы нормальных уравнений, которая состоит из k уравнений с k неизвестными τj с учётом весов pi измеренных величин и значений li свободных членов параметрических уравнений поправок:
В выражениях (14.145) индексы при коэффициентах а соответствуют вторым индексам коэффициентов aij в выражениях (14.144).
Для раскрытия гауссовых сумм в (14.145) составим матрицу коэффициентов aij с весами pi результатов измерений и со свободными членами li (табл. 14.15).
C учётом табл. 14.15 и выражений (14.145) приведём принцип раскрытия гауссовых сумм.
Матрица коэффициентов, свободных членов и весов
| j i | … | j | … | k | li | pi | |||
| a11 | a12 | a13 | a1j | a1k | l1 | p1 | |||
| a21 | a22 | a23 | a2j | a2k | l2 | p2 | |||
| a31 | a32 | a33 | a3j | a3k | l3 | p3 | |||
| … | … | … | … | … | … | … | … | … | … |
| i | ai1 | ai2 | ai3 | aij | aik | li | pi | ||
| … | … | … | … | … | … | … | … | … | … |
| n | an1 | an2 | an3 | anj | ank | ln | pn |
Уравнение 1.
Коэффициент при τ1 равен сумме произведений веса с индексом аргумента (измеренной величины) на квадрат коэффициента 1-го столбца (диагональный коэффициент), т.е.
Коэффициент при τ2 равен сумме произведений веса соответствующего аргумента и коэффициентов 1-го и 2-го столбцов, т.е.
Подобные действия производятся для остальных параметров τ перемножением коэффициентов 1-го столбца и столбца с индексом τ .
Свободный член уравнения 1 равен сумме произведений веса рi, свободного члена li и коэффициента a соответствующего столбца, т.е.
Уравнение 2.
Коэффициент при τ1 равен сумме произведений веса соответствующего аргумента и коэффициентов 2-го и 1-го столбцов, т.е.
Коэффициент при τ2 равен сумме произведений веса с индексом аргумента на квадрат коэффициента 2-го столбца (диагональный коэффициент), т.е.
Коэффициент при τ3 равен сумме произведений веса соответствующего аргумента и коэффициентов 2-го и 3-го столбцов, т.е.
Далее выполняются действия со 2-м столбцом и последующими оставшимися столбцами.
Свободный член уравнения 2 равен сумме произведений веса рi, свободного члена li и коэффициента a соответствующего столбца, т.е.
Вычисление коэффициентов остальных уравнений аналогично. Коэффициенты последнего уравнения с индексом k являются диагональными.
Здесь, как и в коррелатном способе уравнивания, коэффициенты с с противоположными индексами равны друг другу. Следовательно, достаточно определить все диагональные коэффициенты и все коэффициенты, находящиеся справа от диагональных, а остальные записать в уравнениях поправок такими же, как и противоположные им по индексам.
Таким образом, получается система линейных уравнений поправок τj:
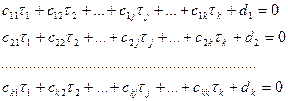
Из решения системы уравнений (14.146) находят значения неизвестных поправок τj к приближенным значениям параметров tj 0 , определяют поправки νi по формулам (14.144) и вычисляют уравненные значения измеренных величин и выбранных параметров Tj (tj = tj 0 + τj).
Приведем последовательность уравнивания геодезических построений параметрическим способом.
Шаг 1.Определяют число необходимых (k), число избыточных (r) в массиве общего числа n измерений xi, имеющих веса pi .
Шаг 2.Осуществляют выбор параметров tj таким образом, чтобы они не имели между собой никаких математических связей, т.е. были независимыми. Число таких параметров должно быть равно k – числу необходимых измерений. При этом все измеренные величины должны выражаться функционально через выбранные параметры tj .
Шаг 3.Определяют вид функций значений xi от аргументов tj , т.е. вид параметрических уравнений связи (14.135).
Шаг 4.Вычисляют приближенные значения tj 0 параметров tj. Часто для этого выполняют предварительные вычисления (обработку) в схемах геодезических построений. Иногда выполняют предварительное уравнивание упрощенными способами, часто способом раздельного уравнивания.
Шаг 5.Вычисляют по формулам (14.141), в общем виде – (14.142) или (14.144), коэффициенты aij и свободные члены li параметрических уравнений поправок vi (14.143), т.е. функции (14.135) приводят к линейному виду.
Шаг 6. Составляют таблицу коэффициентов aij, свободных членов li и весов pi (табл. 14.15) и с помощью неё получают нормальные уравнения (14.145), из решения которых находят значения поправок τj к параметрам tj o .
Шаг 7. Выражают поправки vi к измеренным величинам xi через значения поправок τj (14.143) и определяют их значения.
Шаг 8. Bыполняют уравнивание измеренных величин xi‘ =( xi + vi) и параметров tj =( tj o + τj) и контролируют правильность решения задачи по равенствам (14.135).
Возможны несоблюдения указанных равенств из-за неточного выбора параметров tj либо их приближённых значений tj o . Из-за этого могли использоваться такие величины поправок, при которых необходимо было учитывать нелинейность систем уравнений. Несоблюдение равенств может быть также и из-за погрешностей в вычислениях. Поэтому в первую очередь следует выполнить повторные вычисления (контрольные, лучше во вторую руку: т.е. взаимно попросить кого-нибудь из друзей повторить Ваши вычисления, а Вы такие же вычисления повторно сделаете в его задании; поверьте, так будет и быстрее, и надёжнее).
Если уравнивание, при отсутствии погрешностей в вычислениях, не удовлетворяет условиям (14.135), то полученные значения считают их первым приближением, т.е. уточнёнными значениями tj o , и уравнивают систему вторично.
В качестве рекомендации следует отметить, что предварительные вычисления в уравниваемых построениях лучше выполнять после предварительного, нестрогого уравнивания. Например, в полигонометрическом ходе выполнить уравнивание углов, затем – приращений координат. В цепочке треугольников выполнить предварительное уравнивание углов отдельных треугольников и т.п.
Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Параметрическое уравнивание нивелирной сети
Схема нивелирной сети III класса.
| № ходов | Названия ходов | Н | h | L, км |
| А – Узл 2 | 196,852 | +5,702 | 13,4 | |
| В – Узл 2 | 202,308 | +0,228 | 5,4 | |
| А – Узл 1 | 196,852 | -19,201 | 7,5 | |
| Узл 2 – Узл 1 | -24,895 | 15,6 | ||
| С – Узл 1 | 169,949 | +7,728 | 19,8 |
Обозначим приближенные отметки узловых реперов через xо, yо
Поправки к ним 
Уравненные отметки x, y
x = xо +
y = yо +
Уравнивание будем выполнять в такой последовательности:
1. От репера А по ходу 3 и от репера В по ходу 2, вычисляем приближенные высоты узловых точек
Xо = Hв + h2 = 202,536
yо = Ha + h3 = 177,651
Составим уравнение поправок, причем начинать надо с точки, на которую указывает стрелка
V1 = xо + 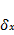
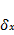
V2 = xо + 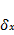
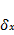
V3 = yо + 

V4 = yо + 
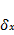

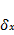
V5 = yо + 

Составим таблицу коэффициентов уравнений поправок. Так как измерения неравноточные, вычисляем веса ходов.
| № | a | b | l,см | S | P=20/L | V,см | V,мм | PV | P 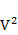 | PlV |
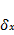 =0,701 =0,701 |  =0,452 =0,452 | |||||||||
| +1 | -1,8 | -0.8 | 1,49 | -1,09 | -10,9 | -1,62 | 1,77 | 2,92 | ||
| +1 | +1 | 3,70 | 0,701 | 7,0 | 2,59 | 1,82 | ||||
| +1 | +1 | 2,67 | 0,452 | 4,5 | 1,21 | 0,55 | ||||
| -1 | +1 | +1,0 | +1 | 1,28 | 0,751 | 7,5 | 0,96 | 0,72 | 0,96 | |
| +1 | -2,6 | -1,6 | 1,01 | -2,148 | -21,5 | -2.17 | 4,66 | 5,64 | ||
| +1 | +3 | -3,4 | 0,6 | 10,15 | 0,97 | 9,52 | 9,52 |
Где S – сумма по строчкам для контроля.
Таблица нормальных уравнений
| a] | b] | l] | s] | Контроль | |
| [Pa | 6,47 | -1,28 | -3,96 | 1,23 | 1,23 = 1,23 |
| [Pb | Учитываем при контроле | 4,96 | -1,35 | 2,33 | 2,33 = 2,33 |
Решение нормальных уравнений.
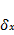 |  | l | S | Контроль | |
| N1 | 6,47 | -1,28 | -3,96 | +1,23 | |
 | -1,00 | 0,198 | 0,612 | -0,190 | -0,190 |
| N2 | 4,96 | -1,35 | 2,33 | ||
 | -0,25 | -0,78 | 0,24 | ||
| N2 | 4,71 | -2,13 | 2,57 | 2,58 | |
 2 2 | -1,00 | 0,452 | -0,546 | -0,548 |

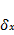
Примечание к таблице:
N1 – первое нормальное уравнение


N2 – второе нормальное уравнение

N2 – преобразованное второе нормальное уравнение ( складываем N2 и




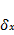
Контроль: Полученные значения подставляем в первое уравнение.
6,47*0,701-1,28*0,452 -3,96 = -0,003
Подставляем полученные значения в уравнение поправок и вычисляем поправки в измеренные превышения.
| N | h | V,мм | h испр |
| +5,702 | -11 | +5,691 | |
| +0,228 | +7 | +0,235 | |
| -19,201 | +5 | -19,196 | |
| -24,895 | +8 | -24,887 | |
| +7,728 | -21 | +7,707 |
h3 – h4 – h2 – (Hb – Ha) = 0
h1 + h4 – h5 – (Hc – Ha) = 0
h2 + h4 – h5 – (Hc – Hb) = 0
Вычисление отметок узловых реперов
Узл.1 = 177,651 + 
Узл.2 = 202,536 + 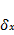
[P 
Вычисляем среднюю квадратическую погрешность единицы веса
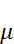

Где n – число ходов (5)

📺 Видео
Уравнивание нивелирных сетей параметрическим методом.Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

Параметрические уравнения прямойСкачать

Основы параметрической формы метода наименьших квадратов (МНК) на примере уравнивания опорных сетей.Скачать

Коррелатный способ. Решение системы условных уравненийСкачать

Уравнивание свободных маркшейдерских и геодезических сетей параметрическим методом.Скачать

№18. Система уравнений с параметром (профильный ЕГЭ)Скачать

ДЗГ clip0016Скачать

Уравнивание ГРО. ГЕОДЕЗИЧЕСКИЕ РАБОТЫСкачать
Системы уравнений. Способ уравнивания коэффициентов - 1Скачать

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Подготовка измерений к уравниванию или предобработка. Основные теоретические моменты.Скачать

Параметрические уравнения (часть 1)Скачать

Рекуррентное уравнивание на примере нивелирной сети. Разбор формул для расчета в Excel.Скачать

Уравнение с параметром | Математика TutorOnlineСкачать