При ионообменной адсорбции происходит стехиометрический обратимый обмен ионов между объемом раствора электролитов и адсорбентом.
Процессы ионного обмена на твердой поверхности характеризуются уравнением Б.П.Никольского:

где 




Графически уравнение Б.П.Никольского изображается прямой, тангенс угла наклона которой и представляют величину константы К.
Примеры решения задач:
1. Рассчитать удельную поверхность адсорбента по изотерме адсорбции бензола на его поверхности. Площадь, занимаемая молекулой бензола, S0=49·10 -20 м 2 .
| p P/PS | 0.024 | 0.08 | 0.14 | 0.20 | 0.27 | 0.35 | 0.46 |
| a·10 3 , моль/кг | 14,9 | 34,8 | 47,2 | 56,8 | 66,3 | 79.3 | 101.0 |
Решение. Проверяют применимость к экспериментальным данным теории БЭТ. С этой целью рассчитывают абсциссу и ординату уравнения изотермы адсорбции БЭТ в линейной форме, т.е.

Результаты вычислений сводят в таблицу 1 и строят график зависимости y=f(x)
| p/ps | y, кг/моль | p/ps | y, кг/моль |
| 0,024 | 1,650 | 0,27 | 5,466 |
| 0,08 | 2,499 | 0,35 | 6,790 |
| 0,14 | 3,449 | 0,46 | 8,343 |
Рис.1 изотерма адсорбции в координатах линейной формы уравнения БЭТ.
Для определения адсорбционной емкости монослоя аm по графику зависимости у=f(x) находят константы уравнения прямой линии: отрезок, отсекаемый на оси ординат при p/ps=0, b0=1.24 кг/моль, и угловой коэффициент прямой b1=15.8 кг/моль. Для сравнения вычисляют b0 и b1
методом наименьших квадратов. Данные для расчёта b0 и b1 приведены в таблице 2.
| n | x | y, кг/моль | xy, кг/моль | x 2 |
| 0,024 | 1,650 | 0,0396 | 5,76·10 -4 | |
| 0,080 | 2,499 | 0,2000 | 6,4·10 -3 | |
| 0,140 | 3,499 | 0,4830 | 1,96·10 -2 | |
| 0,200 | 4,400 | 0,8800 | 4,00·10 -2 | |
| 0,270 | 5,466 | 1,4550 | 7,08·10 -2 | |
| 0,350 | 6,790 | 2,3765 | 0,123 | |
| 0,460 | 8,434 | 3,8778 | 0,212 |
k=13,65 и am=0,0489 моль/кг.
По величине аm рассчитывают удельную поверхность адсорбента:
2. Вычислить предельный адсорбционный объём активированного угля БАУ по изотерме адсорбции бензола (таблица 3). Молярный объём бензола vm=89·10 -6 м 3 /моль.
| p/ps | a, моль/кг | p/ps | a, моль/кг | p/ps | a, моль/кг |
| 1,33·10 -6 | 0,50 | 1,63·10 -2 | 2,25 | 0,327 | 2,86 |
| 2,13·10 -5 | 0,85 | 3,77·10 -2 | 2,39 | 0,460 | 3,00 |
| 1,21·10 -4 | 1,18 | 9,47·10 -2 | 2,56 | 0,657 | 3,19 |
| 5,60·10 -4 | 1,55 | 0,201 | 2,74 | 0,847 | 4,47 |
Решение. Проверяют применимость уравнения (II.15) к экспериментальным данным. С этой целью вычисляют lg a и 

 | lg a |  | lg a |  | lg a |
| 34,52 | -0,3010 | 3,19 | 0,3522 | 0,230 | 0,4564 |
| 21,82 | -0,0706 | 2,03 | 0,3784 | 0,113 | 0,4771 |
| 15,34 | 0,0719 | 1,05 | 0,4082 | 0,033 | 0,5038 |
| 10,58 | 0,1903 | 0,48 | 0,4378 | 0,005 | 0,6503 |
Рис.2 Изотерма адсорбции в координатах линейной формы уравнения М.М.Дубинина.
Как видно из рис.2, экспериментальные точки с хорошим приближением укладываются на прямую линию и, следовательно, уравнение (15) применимо к адсорбции бензола на активированном угле БАУ.
По отрезку, отсекаемому па оси lg a при 

3. По экспериментальным данным сорбции паров воды на активированном угле при Т = 293 К построить кривую капиллярной конденсации. Показать наличие гистерезиса и, используя ветвь десорбции, построить интегральную и дифференциальную кривые распределения пор по радиусам.
аадс ·10 3 ,моль/кг. 3,75 5,3 6;2 8,75 10,4 12, 5 13 ,4
адес·10 3 , моль/кг . . .. 3,75 7,0 7,9 10,0 11,5 13,0 13,4
Vm=18·10 -3 м3/моль, σ= 72,5-10 -3 Дж/м 2 .’
Решение. Строят изотерму капиллярной конденсации в соответствии с условием задачи. Выбирают ряд точек на ветви десорбции (не менее шести—восьми), соответствующих определенным значениям p/pS, и рассчитывают объем пор, заполненных конденсатом, по уравнению V=aVm. Затем для этих же значений по уравнению
рассчитывают максимальный радиус пор, заполненных конденсатом при соответствующих давлениях p/ps. Полученные данные записывают в табл. 5 и строят структурную кривую адсорбента в координатах V=f(r). Из кривой находят ряд значений ΔV/Δr (табл.6) и строят дифференциальную кривую распределения объёма пор по радиусам в координатах ΔV/Δr=f(r)
Таблица.5 Данные для построения интегральной кривой распределения объёма пор по радиусам.
| № точки | P/PS | aдес·10 3 ,моль/кг | V·10 6 ,м 3 /кг | r·10 10 ,м |
| 0,05 0,1 0,2 0,4 0,6 0,8 0,9 0,98 | 0,5 3,7 7,0 7,9 9,0 10,0 10,9 11,5 | 0,9 66,6 126,0 142,0 162,0 180,0 196,0 207,0 | 2,2 4,6 6,6 8,5 11,6 15,5 20,2 26,3 |
Таблица.6 Данные для построения дифференциальной кривой распределения объёма по радиусам.
| ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м |
| 1,5 0,5 |
Рис.3 Интегральная(1) и дифференциальная(2) кривые распределения.
Задачи
1. Ниже приведены экспериментальные данные по адсорбции азота на TiO2 (рутиле) при 75 К:
P·10 2 Па……….60,94 116,41 169,84 218,65 275,25
А, моль/кг……. 0,367 0,417 0,467 0,512 0,567
Постройте график соответствующий линейному уравнению БЭТ. Найдите константы 
занимаемая одной молекулой азота S0=0,16 нм 2 .
2.Окись углерода адсорбируется на слюде; данные при 90 К представлены ниже. Определите, какой изотерме – Лэнгмюра или Фрейндлиха – лучше соответствуют эти данные? Каково значение К для адсорбционного равновесия? Взяв общую поверхность равной 6200см 2 , рассчитайте площадь, занимаемую каждой адсорбированной молекулой.
Vа, см 3 ……………..0,130 0,150 0,162 0,166 0,175 0,180
Р, мм. рт. cт.………. 100 200 300 400 500 600.
3.При измерении адсорбции газообразного азота на активном угле при 194.4К были получены следующие данные:
р·10 -3 , Па……………….1,86 6,12 17,96 33,65 68,89
А·10 3 , м 3 /кг…………..…5,06 14,27 23,61 32,56 40,83
Значения А даны для азота при нормальных условиях.
Рассчитайте, постоянные в уравнение Лэнгмюра и удельную поверхность активированного угля, принимая плотность газообразного азота равной
1,25 кг/м 3 , а площадь занимаемую одной молекулой азота на поверхности адсорбента, равной 0,16 нм 2 .
4.При измерении адсорбции азота на активированном угле при 273 К были получены следующие данные:
А,см 3 /г…………..……0,987 3,04 5,08 7,04 10,31
Р, мм. рт. ст…….……3,93 12,98 22,94 34,01 56,23
Построить график в координатах, в которых происходит спрямление уравнения изотермы Лэнгмюра, и определить константы этого уравнения.
5.Определите константы эмпирического уравнения Фрейндлиха, используя следующие данные об адсорбции диоксида углерода на активном угле при 293 К:
Р·10 -3 , Па…………1,00 4,48 10,0 14,4 25,0 45,2
А·10 2 , кг/кг……….3,23 6,67 9,62 11,72 14,5 17,7.
6.Используя уравнение БЭТ, построить изотерму адсорбции бензола по нижеуказанным данным и рассчитайте удельную поверхность адсорбента по изотерме адсорбции бензола (варианты 1-4):
1. P/Ps.………..0,04 0,08 0,16 0,22 0,27 0,36 0,46
А, моль/кг……. 0,348 0,483 0,624 0,724 0,805 0,928 0,13
2. Р/Рs………. 0,05 0,12 0,19 0,26 0,34 0,44 0,50
А, моль/кг ……. 0,31 0,593 0,795 0,99 1,21 1,525 1,77
3. Р/Рs……….…0,03 0,07 0,12 0,17 0,24 0,31 0,38
А, моль/кг……. 0,196 0,301 0,373 0,423 0,488 0,52 0,625
4. Р/Рs…………. 0,02 0,05 0,11 0,19 0,25 0,3 0,36
А, моль/кг……. 0,104 0,196 0,298 0,387 0,443 0,488 0,55
Площадь, занимаемую молекулой бензола, примите равной 0,49 нм 2 .
7.Используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по данным об адсорбции азота:
А•10 3 , м 3 /кг…………..0,71 0,31 0,93 1,09
Площадь занимаемая молекулой азота в плотном монослое, равна 0,16 нм 2 ,
Плотность азота 1,25 кг/м 3 .
8.При обработке данных по адсорбции азота на графитированной саже при 77 К с помощью графика, соответствующего линейному уравнению БЭТ,
найдено, что тангенс угла наклона прямой составляет 1,5•10 3 , а отрезок, отсекаемый на оси ординат, равен 5 единицам (адсорбция выражена в м 3 азота на 1 кг адсорбента при нормальных условиях). Рассчитайте удельную поверхность адсорбента, предполагая, что площадь, занимаемая одной молекулой азота, равна 0,16 нм 2 .
9.Ниже приведены результаты измерения адсорбции газообразного криптона (при 77,5К) на катализаторе:
А·10 3 , м 3 /кг…………1,27 1,5 1,76 1,9 1,98
Р, Па……………..…13,22 23,99 49,13 75,70 91,22.
Значения А для криптона даны при нормальных условиях. Определите константы уравнения БЭТ и удельную поверхность катализатора, принимая, что один атом криптона занимает площадь 0,195нм 2 , Рs=342,6 Па, плотность криптона равна 3,74 кг/м 3
10.используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по изотерме адсорбции азота:
А, моль/кг……..2,16 2,39 2,86 3,02 3,22 3,33
Площадь занимаемая одной молекулой азота в адсорбционном слое 0,16 нм 2 .
11.По изотерме адсорбции азота определить удельную поверхность адсорбента
(Т=77 К, S0=16,2·10 -20 м 2 ). (Варианты 1-5).
1. Р/Рs………. 0,04 0,09 0,16 0,20 0,30
А, моль/кг… .2,20 2,62 2,94 3,11 3,58
2. Р/Рs…………0,029 0,05 0,11 0,14 0,20
А, моль/кг………..2,16 2,39 2,86 3,02 3,33
3. Р/Рs………….0,02 0,04 0,08 0,14 0,16 0,18
А, моль/кг………..1,86 2,31 2,72 3,07 3,12 3,23
Для следующих двух вариантов объем адсорбированного газа приведен к нормальным условиям:
4. Р/Рs…………….…0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 м 3 /кг……………..0,70 1,10 1,17 1,32 1,45 1,55
5. Р/Рs……………….0,029 0,05 0,11 0,14 0,18 0,20
А·10 2 м 3 /кг……..……..0,48 0,54 0,64 0,68 0,72 0,75
12.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49•10 -20 м 2 . Объем адсорбированного газа приведен к нормальным условиям (варианты 1-4):
1. Р/Рs…………………….0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 , м 3 /кг………………..0,86 1,20 1,40 1,60 1,80 1,90
2. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг……….………..1,15 1,37 1,55 1,71 1,86 1,99
3. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг………………..0,89 1,09 1,27 1,45 1,60 1,78
4. Р/Рs…………………….0,08 0,16 0,25 0,35 0,45 0,52
А·10 2 , м 3 /кг………..… ……1,03 1,37 1,70 1,99 2,44 2,82
13.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49·10 -20 м 2 (варианты 1-3).
1. Р/Рs……………..0,05 0,10 0,15 0,20 0,30 0,40
А, моль/кг…. ………0,36 0,51 0,60 0,68 0,82 0,98
2. Р/Рs…………. ….0,06 0,12 0,20 0,30 0,40 0,50
А, моль/кг…. ………..0,08 0,16 0,25 0,35 0,45 0,52
3. Р/Рs…………. ….0,46 0,61 0,76 0,89 1,09 1,26
14.Построить изотерму адсорбции нитролигнина на глине и определить константы уравнения Фрейндлиха по следующим экспериментальным данным:
Концентрация водного раствора нитролигнина
Г·10 3 , кг/кг……………………5,0 12,0 21,0 26,0 35,0 38,0.
15.Пользуясь экспериментальными данными ионного обмена ионов кальция (Г1с1) и натрия (Г2с2) на синтетическом катионите, определить графически константу уравнения Никольского К:



16.Пользуясь константами уравнения Фрейндлиха k=4,17·10 -3 , 1/n=0,4, рассчитать и построить изотерму адсорбции углекислого газа на угле для следующих интервалов давления: 100·10 2 , 200·10 2 , 400·10 2 , 500·10 2 Н/м 2 .
17. Пользуясь константами уравнения Фрейндлиха k=3,2·10 -3 , 1/n=0,6 построить кривую адсорбции углекислого газа на угле в интервале давлений от 5·10 2 до 25·10 2 Н/м 2 .
18. По данным сорбции углекислого газа на угле построить изотерму адсорбции и определить константы изотермы адсорбции Фрейндлиха:
Р·10 -2 , Н/м 2 ……………..5,0 10,0 30,0 50,0 75,0 100,0
Г·10 3 , кг/кг……………..30, 5,5 16,0 23,0 31,0 35,0.
19. При изучении реакций обмена Mg-ионов из чернозема с ионами Ca из внесенных минеральных удобрений получены следующие результаты:
Концентрация ионов в растворе Количество сорбированных катионов
С·10 3 , кмоль/м 3 Г·10 5 ,кмоль/кг
2,41 4,75 8,12 42,88
2,25 5,00 7,70 43,30
2,00 5,10 6,90 44,10
1,84 5,50 6,10 44,90
1,53 5,87 4,54 46,46
1,37 5,99 4,12 46,88
Графическим методом определить константу уравнения Никольского.
20.Оределить константу уравнения Никольского К, используя экспериментальные данные реакций обмена ионов Ca из почвы на ионы Na из раствора натриевой соли.
Концентрация ионов в растворе Na…3,26 6,60 13,80 21,25 38,41 65,19
С·10 3 , кмоль/м 3 Ca.…37,84 36,72 34,62 31,87 26,16 17,10
Количество сорбированных Na….0,28 0,60 1,20 1,89 3,18 7,62
ионов Г·10 5 , кмоль/кг Ca…39,72 39,56 39,40 38,93 38,68 37,40
21.Пользуясь экспериментальными данными реакций обмена ионов ионов Na из раствора натриевой соли на ионы Mg из почвы, определить графически константу уравнения Никольского:
Концентрация ионов в растворе Количество сорбированных ионов
С·10 3 ,кмоль/м 3 на почве Г.10 5 , кмоль/кг
13,82 41,92 1,16 25,40
21,25 38,30 1,89 26,13
38,19 31,90 3,62 27,20
65,0 21,14 8,01 29,32
79,25 14,73 11,66 32,84
22. Используя экспериментальные данные адсорбции анилина из его водного раствора на угле, определить графически константы уравнения Лэнгмюра и построить изотерму адсорбции для следующих с1:
C1·10 4 , кмоль/м 3 ……………………3 5 10 15 20
анилина с·10 4 , кмоль/ м …………1,0 4,0 7,5 12,5 17,5
А·10 9 ,кмоль/м 2 …………….……0,3 0,58 0,70 0,87 0,92
23.По экспериментальным данным построить кривую адсорбции углекислого газа на цеолите при 293º и с помощью графического метода определить константы уравнения Лэнгмюра:
Р·10 -2 , н/м 2 ……………….1,0 5,0 10,0 30,0 75,0 100,0 200,0
А·10 3 , кг/кг………………35,0 86,0 112,0 152,0 174,0 178,0 188,0
24.Используя уравнение Лэнгмюра, вычислить величину адсорбции азота на цеолите при давлении р=2,8·10 2 , если А∞=38,9·10 -3 кг/кг, а k=0,156·10 -2 .
25. Найти площадь, приходящуюся на одну молекулу в насыщенном адсорбционном слое анилина на поверхности его водного раствора, если предельная адсорбция А∞=6,0·10 -9 кмоль/м
26.По экспериментальны данным адсорбции углекислого газа на активированном угле, найти константы уравнения Лэнгмюра, пользуясь которыми рассчитать и построить изотерму адсорбции:
P·10 -2 , Н/м2……………..9,9 49,7 99,8 200,0 297,0 398,5
Г·10 3 , кг/кг……………..32,0 70,0 91,0 102,0 107,3 108,0.
27.По константам уравнения Лэнгмюра А∞=182·10 -3 и k=0,1·10 -2 рассчитать и построить изотерму адсорбции углекислого газа на активированном угле в пределах следующих равновесных давлений газа: 10·10 2 – 400·10 2 Н/м.
28.Построить кривую адсорбции углекислого газа на активированном угле при 231 º и определить константы эмпирического уравнения Фрейндлиха, пользуясь следующими экспериментальными данными:
Р·10 -2 , Н/м 2 ………………10,0 44,8 100,0 144,0 250,0 452,0
А·10 3 , кг/кг……………….32,3 66,7 96,2 117,2 145,0 177,0.
29. Используя константы эмпирического уравнения Фрейндлиха k=1,6·10 -3 и 1/n=0,48, построить кривую адсорбции углекислого газа на активированном угле при 271 º в интервале давлений от 2·10 2 до 30·10 2 Н/м 2 .
30. Определить постоянные эмпирического уравнения Фрейндлиха, используя следующие данные для адсорбции при 231К углекислого газа на угле из коксовой скорлупы:
Р, Па·10 -3 ……………….1,000 4,480 10,000 14,40 25,0 45,2
А, кг/кг·10 2 ………………3,23 6,67 9,62 11,72 14,5 17,7.
31. Вычислите площадь поверхности катализатора, если для образования монослоя на нем должно адсорбироваться 103 см 3 /г азота (объем приведен к 760 мм рт.ст. и 0ºС). Адсорбция измеряется при температуре 195ºС. Эффективная площадь, занимаемая молекулой азота при этой температуре, равна 16,2 А 2 .
32.Площадь поверхности 1 г активированного угля равна 1000 м 2 . Какое количество аммиака может адсорбироваться на поверхности 45 г угля при 45ºС и 1 атм, если принять в качестве предельного случая полное покрытие поверхности? Диаметр молекулы аммиака равен 3·10 -10 м. Принимается, что молекулы касаются друг друга так, что центры четырех соседних сфер расположены в углах квадрата.
33. Ниже представлены данные по хемосорбции водорода на порошке меди при 25ºС. Подтвердите, что они подчиняются изотерме Ленгмюра. Затем найдите значение К для адсорбционного равновесия и адсорбционный объем, соответствующий полному покрытию.
Р, мм рт ст…………………..0,19 0,97 1,90 4,05 7,5 11,95
Vа, см 3 ……………………….0,042 0,163 0,221 0,321 0,411 0,471.
34. Определите, какая изотерма – Лэнгмюра или Фрейндлиха – лучше соответствует данным для адсорбции метана на 10 г сажи при 0ºС, приведенным ниже:
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Химия : Электроаналитические методы
Электрохимические методы используются довольно часто, поскольку они позволяют получить богатую экспериментальную информацию о кинетике и термодинамике многих химических систем. Вследствие многообразия, высокой чувствительности и точности результатов, безынерционности, быстроте проведения анализа и возможности автоматизации электрохимические методы анализа давно и плодотворно применяют в химии, биологии, медицине и в мониторинге объектов окружающей среды.
Все электрохимические методы анализа и исследования основаны на изучении и использовании процессов, протекающих на поверхности электрода или в приэлектродном слое. Любой электрический параметр (потенциал, сила тока, сопротивление и др.), функционально связанный с концентрацией определяемого компонента и поддающийся правильному измерению, может служить аналитическим сигналом.
В соответствии с областями измерений электрохимические методы анализа делят на пять групп: потенциометрические, вольтамперометрические, кулонометрические и кондуктометрические. Инструментальный базис и теоретические основы этих методов развиты до такой степени, что они легко могут применяться даже неспециалистами. Однако в настоящее время следует отметить невосприятие электроаналитических методов теми людьми, которые не имеют опыта их применения и в недостаточной степени знакомы с электрохимией.
В работе будут рассмотрены только важные электроаналитические методы вместе с наиболее существенной информацией о возможности их применения потенциальными пользователями. В своем реферате я поставила следующие цели:
· Рассмотреть наиболее важные электроаналитические методы
· Выяснить пригодность каждого метода для определения различных ионов
· Рассмотреть достоинства и недостатки каждого метода
Известно, что потенциал электрода может меняться при изменении активности или концентрации одного или нескольких веществ в растворе, в который он погружен. Таким образом, измеряя потенциал можно получить количественную характеристику о составе раствора. Потенциометрические методы заключаются в измерении разности потенциалов между парой подходящих электродов, опущенных в анализируемый раствор.
Установка для измерения разности потенциалов состоит из индикаторного электрода, электрода сравнения, анализируемого раствора и потенциометра. Подключая электроды к соответствующим клеммам измерительного прибора, мы получаем возможность измерения разности потенциалов между двумя электродами или, как говорят аналитики, измеряем потенциал индикаторного электрода относительно электрода сравнения.
1.1 Индикаторные электроды
Известны два основных типа индикаторных электрода для потенциометрических измерений: металлические и мембранные электроды.
Металлические электроды можно изготавливать из различных металлов (Ag, Cu, Hg, Pb, Cd) способных давать обратимые реакции. Некоторые металлы (Al, Ni, Co, W, Cr) не могут быть использованы в качестве индикаторных, так как на их поверхности присутствуют окисные пленки либо дефекты кристаллической структуры, что приводит к получению плохо воспроизводимых потенциалов.
Мембранные индикаторные электроды бывают четырех видов:
1) электроды со стеклянными мембранами;
2) электроды с жидкими или пленочными мембранами;
3) электроды с твердыми мембранами;
4) электроды с газочувствительными мембранами.
Расчет потенциала металлических электродов
Электроды I рода (рис. 1.1) представляют собой металлическую проволоку или пластинку, опущенную в раствор соли. Пример:
Рисунок 1.1 — Электрод I рода
Металлические индикаторы І рода используют в анализе катионов металлов, чаще всего при потенциометрическом титровании.
Электроды ІІ рода (рис. 1.2) — металлическая проволока или пластинка, находящаяся в контакте с малорастворимым соединением катиона металла и опущенная в раствор соли, содержащей анионы малорастворимого соединения.
Рисунок 1.2 — Электрод ІІ рода
Электроды ІІ рода используют в качестве индикаторных, для определения активности концентрации анионов то есть когда его используют как индикаторный.
1.2 Электроды сравнения
1) Хлоридсеребрянные электроды
2) Каломельные электроды
1.3 Мембранные индикаторные электроды
А) Стеклянные мембранные электроды
Оказалось, что измерить рН раствора наиболее удобно с использованием стеклянного мембранного электрода, содержащего мембрану, разделяющую два раствора с различной активностью ионов водорода.
Состав стекла, кроме основного компонента SiO2 содержит оксиды щелочных и щелочноземельных металлов, что позволяет такой мембране участвовать в равновесном объеме ионами водорода в анализируемом растворе. «Corning»: 72% SiO2, 22% CaO, 6% Na2O (H2O, K2O).
Стеклянный электрод изготавливают путем припаивания тонкого наконечника шарика из рН-чувствительного стекла к концу толстостенной стеклянной трубки заполненной раствором HCl с активностью ионов водорода равной единице (). В раствор погружают серебряную проволоку покрытую AgCl. Таким образом, — внутренний электрод сравнения. Ячейка для измерения рН содержит стеклянную рН-чувствительную мембрану, которая разделяет раствор, в который опущен электрод сравнения и внешний анализируемый раствор с опущенным внешним электродом сравнения, чаще всего хлоридсеребрянным.
Схема потенциометрической ячейки для измерения рН
Потенциал мембраны представляет собой разность потенциалов, которая формируется на внешней и внутренней поверхности мембраны за счет ионного обмена.
Потенциал ячейки будет определяться потенциалами двух электродов сравнения; потенциалом мембраны и еще одной величиной, которую называют потенциалом ассиметрии.
Потенциал ассиметрии возникает даже в случае, если мы используем совершенно идентичные внешние и внутренние электроды сравнения.
Появление этой величины связывают с различным диаметром внешней и внутренней поверхности шарика, что может привести к различным напряжениям в стеклянной матрице мембраны и соответственно к различной скорости обмена ионами водорода на внешней и внутренней поверхности мембраны.
По мере использования электрода наружная рабочая поверхность шарика загрязняется молекулами различных веществ, что приводит к повышению потенциала ассиметрии и соответственно погрешностям в измерении величины рН. Потому необходимо тщательно отмывать стеклянный электрод после погружения его в растворы сложного состава рН 5,5?6,0.
Сам процесс обмена ионами водорода между раствором и стеклянной мембранной осуществляется в тонком гелевом слое, который образуется на обеих поверхностях мембраны при выдерживании электрода в дистиллированной воде.
При выдерживании стеклянного электрода в воде в гелевом слое образуются так называемые силанольные группы .
Если выдержать мембрану в растворе соляной кислоты определенной концентрации, ионы водорода, проникая в поры мембраны, образуют связь с неподеленной парой кислорода силанольной группы.
Наличие неподеленной пары для атома кислорода силанольной группы позволяет ионам водорода, протекающим извне образовывать связь -O:H+. Именно для того, чтобы мембрана стеклянного электрода насытилась ионами Н+, электрод вымачивают в течение нескольких дней в растворе 0,1М HCl и именно эти ионы участвуют потом в ионном обмене при опускании электрода в анализируемый раствор. В более старых теориях формирования потенциала рН-чувствительной мембраны оговаривалось, что ионы Н+ из анализируемого раствора эквивалентно обменивается с ионами щелочных металлов из матрицы мембраны.
Перечисленные теории объясняют физический смысл операций, которые необходимо проводить со стеклянным электродом для получения удовлетворительных и воспроизводимых результатов измерения.
1. «Вымачивание» нового электрода в 0,1М растворе HCl не менее трех дней.
2. Хранение рабочих электродов исключительно в Н2Одист рН 5,5?6,0
В области сильнокислых (рН 12) растворов возможно появление ошибок в измерении величины рН. Так называемая щелочная ошибка (рН>12) связана с участием в формировании потенциала электрода ионов Na+ или К+, которые также способны участвовать в ионном обмене. Ошибки измерения рН в сильнокислой среде (рН
Видео:Алгебра 8 класс Никольский Ч12 п 4.2-4.6Скачать

5.3.4. Термодинамика ионного обмена
Ионный обмен — обратимый процесс, приводящий, как правило, к установлению термодинамического равновесия. Это обстоятельство позволяет легко регенерировать иониты после их использования. Катиониты регенерируют 0,2-0,5 н. раствором кислоты, аниониты — раствором щелочи, слабоосновные аниониты – раствором соды. При средней степени сшитости ионитов положение ионообменного равновесия определяется в значительной степени природой обменивающихся ионов.
Положение равновесия обмена, например, противоионов типа (1) на ионы типа (2) определяется термодинамической постоянной K:
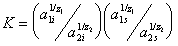
где 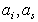
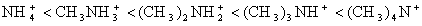
В приведенных рядах неорганических катионов падает их склонность к гидратации, а в случае органических ионов растет интенсивность дисперсионных взаимодействий с матрицей. Тепловой эффект ионного обмена, не осложненного побочными взаимодействиями, не превышает 4-8 кДж/моль. Поэтому постоянная ионообменного равновесия мало зависит от температуры.
В связи с тем, что активность ионов в ионообменнике ни определить, ни рассчитать по косвенным определениям невозможно, часто при выражении постоянной равновесия ионнного обмена активности ионов в ионообменнике заменяют их массой, тогда уравнение приводят к виду
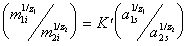
В этой форме уравнение известно как уравнение Никольского.
Если обмениваются ионы одного знака заряда, т.е. при z1 = z2, то
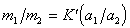
Для разбавленных растворов электролитов, обменивающихся ионами с ионообменником можно активность заменить на концентрацию, тогда
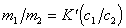
Уравнение (1.5.54) позволяет рассчитать постоянную равновесия ионообменной адсорбции, имеющую большое практическое применение, по результатам определения концентрации ионов в растворе до и после ионного обмена, но следует помнить, что найденная таким образом постоянная не будет строгой термодинамической характеристикой процесса.
Скорость установления равновесия обычно ограничивается диффузией обменивающихся ионов через границу раздела фаз «ионит — раствор» или, чаще, внутри гранул, волокон или мембран ионита.
🎦 Видео
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Показательные уравнения. 11 класс.Скачать

разбор "алгебры" Никольского 7 классСкачать

27. Вычисление предела функции №1. Примеры 1-4Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Алгебра 8 класс Никольский Ч 14 п 5.1-5.4Скачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Никольский 10 класс N146 (б). Решение показательных уравнение.Скачать

Математический анализ, 5 урок, Непрерывность функцииСкачать






