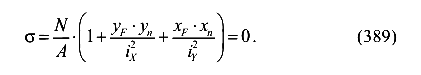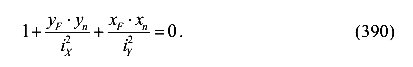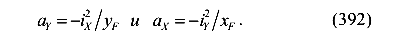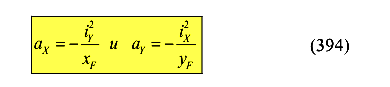- Внецентренное растяжение (сжатие)
- Определение положения нулевой линии (нейтральной оси) при внецентренном растяжении (сжатии)
- Определение положения нулевой линии (нейтральной оси) при внецентренном растяжении (сжатии)
- ПроСопромат.ру
- Технический портал, посвященный Сопромату и истории его создания
- Внецентренное растяжение или сжатие
- 🎥 Видео
Внецентренное растяжение (сжатие)
Внецентренное растяжение (сжатие) вызывается силой, параллельной оси бруса, но не совпадающей с ней (рис. 10.6).
Внецентренное растяжение (сжатие) может быть сведено к осевому растяжению (сжатию) и косому изгибу, если перенести силу P в центр тяжести сечения. Внутренние силовые факторы в произвольном поперечном сечении бруса равны:

где y p , z p — координаты точки приложения силы.
На основании принципа независимости действия сил напряжения в точках поперечного сечения при внецентренном растяжении (сжатии) определяются по формуле:

где 
Выражение в скобках в уравнении (10.15) показывает во сколько раз напряжения при внецентренном растяжении (сжатии) больше напряжений центрального растяжения.
Уравнение нейтральной линии определяем из (10.15), приравнивая правую часть (10.15) нулю. После сокращения на P / F получим

Таким образом, нейтральная линия при внецентренном растяжении (сжатии) не проходит через центр тяжести сечения. Нейтральная линия отсекает на осях координат отрезки

Из формулы (10.17) видно, что точка приложения силы и нейтральная линия всегда расположены по разные стороны от центра тяжести сечения , причем положение нейтральной линии определяется координатами точки приложения силы (рис. 10.7).
При приближении точки приложения силы к центру тяжести сечения ( a и b по абсолютной величине возрастают) нейтральная линия будет удаляться от центра. При этом в сечении увеличивается доля напряжений одного знака, так как уменьшаются напряжения от изгиба. При удалении точки приложения силы от центра тяжести сечения ( a и b по абсолютной величине убывают) нейтральная линия будет приближаться к центру. При этом в сечении увеличивается доля напряжений разного знака, так как возрастают напряжения от изгиба. В пределе при a = b =0 нейтральная линия удаляется в бесконечность. В этом случае будет иметь место центральное растяжение (сжатие) бруса.
Всегда можно найти такое положение точки приложения силы, при котором нейтральная линия будет касаться контура сечения, нигде не пересекая его. В этом случае в сечении напряжения будут только одного знака. Зона вблизи центра тяжести сечения, приложение продольной нагрузки в которой вызывает появление во всех точках сечения напряжений только одного знака, называется ядром сечения . До тех, пока точка приложения силы находится внутри ядра, нейтральная линия не пересекает контур сечения и напряжения во всем сечении будут одного знака. Если точка приложения силы расположена вне ядра, то нейтральная линия пересекает контур сечения, и тогда в сечении будут действовать напряжения разного знака. Указанное обстоятельство необходимо учитывать при расчете элементов конструкций из хрупких материалов, плохо воспринимающих растягивающие нагрузки. В этом случае необходимо прикладывать внешние силы так, чтобы во всем сечении действовали только напряжения сжатия. Для этого точка приложения равнодействующей внешних сил должна находиться внутри ядра сечения.
Расчет на прочность при внецентренном растяжении (сжатии) производится так же, как и при косом изгибе, — по нормальному напряжению в опасной точке поперечного сечения. Опасной является точка сечения, наиболее удаленная от нейтральной линии. Однако, в тех случаях, когда в этой точке действует напряжение сжатия, а материал элемента конструкции хрупкий, опасной может быть точка, в которой действует наибольшее растягивающее напряжение. Эпюра напряжений строится на оси, перпендикулярной к нейтральной линии сечения и ограничена прямой линией. Условие прочности имеет следующий вид:

где y A , z A — координаты опасной точки, а [ σ ] — допускаемое напряжение на растяжение и сжатие.
Видео:Внецентренное растяжение-сжатие. Нейтральная линия. Нормальные напряженияСкачать

Определение положения нулевой линии (нейтральной оси) при внецентренном растяжении (сжатии)
Видео:Сопротивление материалов. Лекция: косой изгиб и внецентренное растяжение-сжатиеСкачать

Определение положения нулевой линии (нейтральной оси) при внецентренном растяжении (сжатии)
Линия, соединяющая все точки сечения колонны, в которой напряжения равны нулю, называется нулевой линии (нейтральной оси).
Пусть произвольная точка расположена на нулевой линии. Обозначим ее координаты 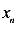
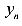
Так как 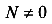
Перенесем 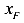
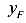
Так как 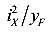
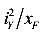
Тогда уравнение можно записать в следующем виде
Полученное уравнение — это уравнение прямой линии в отрезках. Здесь
это отрезки, отсекаемые нулевой линией на главных центральных осях инерции (рис. 120).
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Дополнительные страницы которые вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:21. Внецентрненное растяжение-сжатие стойки ( практический курс по сопромату )Скачать

ПроСопромат.ру
Видео:Внецентренное растяжение и сжатие (Сопромат)Скачать

Технический портал, посвященный Сопромату и истории его создания
Видео:Изгиб Л.3 \ внецентренное растяжение-сжатиеСкачать

Внецентренное растяжение или сжатие
Рассмотрим важный частный случай изгиба с растяжением или сжатием. Этот вид деформации получится, если к стержню будут приложены две равные и противоположно направленные силы Р, линия действия которых не будет совпадать с центральной осью стержня, а будет ей параллельна.
Эксцентриситет (е) линии действия силы:
В результате переноса получаем три силовых фактора: нормальная сила Р, изгибающий момент вокруг оси Х, Мх=Р . у p и изгибающий момент Му= – Р . хр. Нормальные напряжения будут определяться по формуле:
перепишем эти формулы в другом виде
Если площадь А вынести за скобки

По этим формулам можно вычислить напряжения в любой точке сечения.
Положение нулевой (нейтральной) линии определим, приравнивая (1) к нулю:
По этому уравнению можно определить отрезки, отсекаемые нулевой линией на осях координат. Обозначим эти отрезки через ах и ау. Положим ах=0, получим:

Нейтральная линия не проходит через ту четверть, где приложена сила Р, так как здесь знаки компоненты нормального напряжения одинаковы.
Очевидно, что если точка приложения силы будет передвигаться по прямой, параллельной одной из главных осей инерции, то нейтральная линия будет поворачиваться вокруг некоторой точки, лежащей на другой оси.
Если координата ур=const, а ах меняется, то нейтральная линия, меняя своё положение в сечении, все время проходит через точку Д на оси Y. Когда хр=0 (точка 1 на оси у), то нейтральная линия параллельна оси Х.
Если точка приложения силы будет перемещаться по прямой, наклонённой к обеим осям главных моментов инерции сечения, то нейтральная линия опять-таки будет поворачиваться вокруг некоторой точки, но уже не лежащей в этом случае ни на одной из главных осей.
Нейтральная линия проходит через точку Н и поворачивается вокруг неё.
Ядро сечения
Из формул (2) видно, что с уменьшением координат точки приложения силы расстояния ау и ах увеличиваются, то есть точки пересечения нейтральной линии с осями координат удаляются от центра. При некоторых значениях ур и хр нейтральная линия окажется за пределами сечения, тогда во всём сечении напряжения будут иметь один знак.
Хрупкие материалы, как известно, плохо работают на растяжение. Между тем, части сооружений подвергаются действию сжимающей нагрузки, нередко их делают из хрупких материалов. Для того, чтобы и при внецентренном приложении сжимающей нагрузки в материале не возникало растягивающих напряжений, нужно ограничить величину эксцентриситета нагрузки, не выводить точку приложения за пределы некоторой области в сечении.
Область, расположенная вокруг центра сечения, в пределах которой должна находиться точка приложения продольной сжимающей или растягивающей силы, чтобы напряжения в сечении были одного знака, называется ядром сечения:
Границы ядра сечения определяются из (2).
🎥 Видео
Внецентренное растяжение и сжатиеСкачать

Внецентренное растяжение - сжатие. Ядро сеченияСкачать

7.2.3а Внецентренное растяжение/сжатиеСкачать

Внецентренное сжатие (растяжение)_часть 1Скачать

Внецентренное сжатие (растяжение) (2021 г)Скачать

Изгиб С.5: Косой изгиб / Внецентренное растяжение-сжатиеСкачать

Сопротивление материалов. Лекция 13 (косой изгиб, внецентренное растяжение/сжатие).Скачать

ANSYS Сопротивление материалов. I-07 (внецентренное растяжение/сжатие).Скачать

Внецентренное сжатие. Нахождение максимальных и минимальных напряжений в сеченииСкачать

Определение усилий, напряжений и перемещений при растяжении-сжатииСкачать

Ядро сеченияСкачать

Внецентренное растяжение и сжатиеСкачать

Сопротивление материалов. I-01 (косой изгиб, внецентренное растяжение/сжатие, введение).Скачать

Внецентренное растяжение и сжатиеСкачать