В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.
- Определение уравнения прямой на плоскости
- Общее уравнение прямой линии
- Уравнение прямой в отрезках
- Уравнение прямой с угловым коэффициентом
- Каноническое уравнение прямой на плоскости
- Параметрические уравнения прямой на плоскости
- Нормальное уравнение прямой
- Геометрия.8 класс. Индивидуальные карточки №213
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Математические диктанты по геометрии, 9 класс
- Просмотр содержимого документа «Математические диктанты по геометрии, 9 класс»
- 🎦 Видео
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Определение уравнения прямой на плоскости
Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .
Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.
Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.
Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.
Видео:Видеоурок "Канонические уравнения прямой"Скачать

Общее уравнение прямой линии
Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .
Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .
Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .
Поясним некоторые важные аспекты темы.
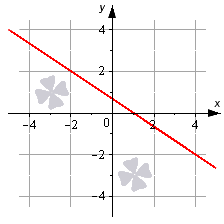
Посмотрите на рисунок.
Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.
Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .
Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .
Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .
Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.
Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнение прямой в отрезках
Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.
Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.
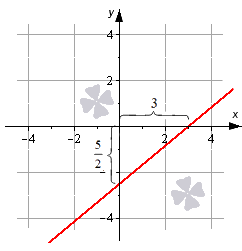
Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.
Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».
Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Уравнение прямой с угловым коэффициентом
Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .
Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .
Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.
Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).
Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .
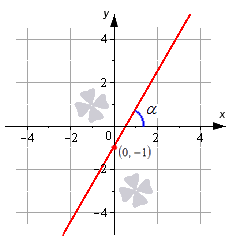
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .
Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3
Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.
Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.
Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Каноническое уравнение прямой на плоскости
Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.
Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .
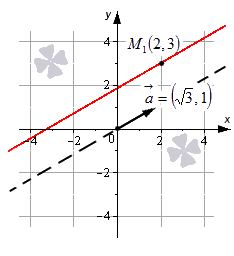
Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.
Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .
В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.
Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.
Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Параметрические уравнения прямой на плоскости
Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.
Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .
Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .
Предположим, что λ = 0 .
Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.
Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.
Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .
Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».
Видео:11. Прямая в пространстве и ее уравненияСкачать

Нормальное уравнение прямой
Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .
Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .
Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.
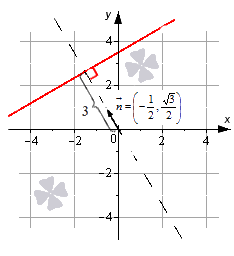
Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .
Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .
Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.
Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».
Видео:Составляем уравнение прямой по точкамСкачать

Геометрия.8 класс. Индивидуальные карточки №213
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Диагонали четырехугольника ABCD в точке пересечения делятся пополам. Угол А равен 70°. Чему равен угол В?
2. Дан выпуклый четырехугольник ABCD. Назовите его диагонали.
3. Один из углов ромба равен 40°. Чему равны остальные три угла ромба?
4. Два угла трапеции равны 32° и 125°. Чему равны два другие угла?
1. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка 3 км/ч. Какое расстояние (в км) будет между ними через 30 мин?
2. Два парохода вышли из порта, следуя один на север,
другой на запад. Скорости их равны 15 км/ч и 20 км/ч. Какое расстояние будет между ними через 2 ч?
1. Запишите окончание предложения:
1) уравнение прямой имеет вид … ;
2) уравнение прямой является частным видом … ;
3) если b = 0 и a ≠ 0, то уравнение прямой ax + by = c задаёт … ;
4) если b ≠ 0, то уравнение прямой ax + by = c задаёт … ;
5) уравнение невертикальной прямой удобно записывать в виде … ;
6) если прямая задана уравнением y = kx + p, то коэффициент k называют … ;
7) если невертикальная прямая образует с положительным направлением оси абсцисс угол α, то угловой коэффициент прямой равен … ;
8) прямые y = k1x + b1 и y = k2x + b2 параллельны тогда и только тогда, когда … .
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 930 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 304 человека из 68 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 593 936 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 29.01.2021
- 193
- 0
- 29.01.2021
- 71
- 0
- 29.01.2021
- 117
- 0
- 29.01.2021
- 102
- 0
- 29.01.2021
- 70
- 0
- 29.01.2021
- 77
- 1
- 29.01.2021
- 71
- 0
- 29.01.2021
- 100
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 29.01.2021 151
- PPTX 289.6 кбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Беч Вероника Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 8 месяцев
- Подписчики: 2
- Всего просмотров: 142277
- Всего материалов: 1344
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Видеоурок "Общее уравнение прямой"Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие
Время чтения: 15 минут
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
Минпросвещения России подготовит учителей для обучения детей из Донбасса
Время чтения: 1 минута
Студенты российских вузов смогут получить 1 млн рублей на создание стартапов
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Математические диктанты по геометрии, 9 класс
Предложенные диктанты адресованы учителям, работающим по учебнику «Геометрия. 9 класс» (авторы А.Г. Мерзляк В.Б. Полонский, М.С. Якир), но могут быть использованы и учителями, работающими по другим учебникам.
Просмотр содержимого документа
«Математические диктанты по геометрии, 9 класс»
Математические диктанты по геометрии
(9 класс, учебник авт. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир)
Диктант 1 по теме «Тригонометрические функции угла от 0° до 180°»
Запишите окончание предложения:
1) косинусом угла α, где 0° ≤ α ≤ 180°, которому соответствует точка M единичной полуокружности, называют … ;
2) синусом угла α, где 0° ≤ α ≤ 180°, которому соответствует точка M единичной полуокружности, называют … ;
3) синус угла α, где 0° ≤ α ≤ 180°, не меньше … ;
4) синус угла α, где 0° ≤ α ≤ 180°, не больше … ;
5) косинус угла α, где 0° ≤ α ≤ 180°, не меньше … ;
6) косинус угла α, где 0° ≤ α ≤ 180°, не больше … ;
7) косинус тупого угла является числом … ;
8) если косинус угла меньше нуля, то этот угол … ;
9) основным тригонометрическим тождеством называют равенство … ;
10) тангенсом угла α, где 0° ≤ α ≤ 180° и α ≠ 90°, называют … ;
11) тангенс не определён для угла … ;
12) котангенсом угла α, где 0°
13) котангенс не определён для углов … .
Сравните с нулём:
1) sin 129°; 3) cos 102°; 5) ctg 38°;
2) cos 73°; 4) tg 0°; 6) tg 136°.
Острым, прямым или тупым является угол α, где 0°
1) cos α = 0; 3) sin α ctg α
2) tg α 0; 4) cos α tg α 0?
Существует ли угол α, для которого:
1) sin α = 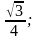
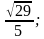
Может ли синус острого угла быть равным косинусу этого угла? Ответ обоснуйте.
Может ли синус тупого угла быть равным косинусу этого угла? Ответ обоснуйте.
Диктант 2 по теме «Теорема косинусов»
Запишите окончание предложения:
1) квадрат стороны треугольника равен … ;
2) сумма квадратов диагоналей параллелограмма равна … .
Пусть a, b и c — стороны треугольника, причём a — его наибольшая сторона. Запишите окончание предложения:
1) если a 2 b 2 + c 2 , то треугольник … ;
2) если a 2 b 2 + c 2 , то треугольник … ;
3) если a 2 = b 2 + c 2 , то треугольник … .
Дан треугольник BCD. Используя теорему косинусов, запишите, чему равен квадрат стороны BD.
В треугольнике ABC известно, что AB = 3 см, BC = 4 см, QB = 30°. Найдите сторону AC.
В треугольнике ABC известно, что AB 2 BC 2 + AC 2 . Укажите наибольший угол треугольника.
Стороны треугольника равны 32 см, 1 см и 5 см. Найдите наибольший угол треугольника.
Две стороны треугольника равны 6 см и 8 см. Какую наименьшую длину, равную целому числу сантиметров, должна иметь третья сторона треугольника, чтобы угол между данными сторонами был тупым?
Диктант 3 по теме «Теорема синусов»
Запишите окончание предложения:
1) хорда окружности равна произведению диаметра на … ;
2) стороны треугольника пропорциональны … ;
3) если a — сторона треугольника, α — противолежащий ей угол, то радиус окружности, описанной около треугольника, можно вычислить по формуле … .
В треугольнике ABC известно, что AB = 8 см, sin C = 0,4, sin B = 0,8. Найдите сторону AC.
В треугольнике ABC известно, что AB = 12 см, BC = 9 см, sin A = 0,6. Найдите sin C.
В остроугольном треугольнике DEF известно, что sin D sin F sin E. Укажите наибольшую сторону треугольника DEF.
В треугольнике ABC известно, что BC = 7 см, sin A = 0,35. Найдите радиус окружности, описанной около треугольника ABC.
Радиус окружности, описанной около треугольника ABC, равен 10 см, sin A = 0,18. Найдите сторону BC.
Радиус окружности, описанной около треугольника ABC, равен 24 см, AC = 16 см. Найдите sin B.
В треугольнике ABC известно, что 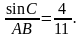
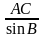
В треугольнике ABC известно, что 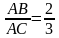
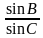
Диктант 4 по теме «Формулы для нахождения площади треугольника»
Запишите формулу для вычисления площади S треугольника, если известны его стороны a и b и угол γ между ними.
Запишите формулу Герона для вычисления площади S треугольника.
Запишите формулу для вычисления площади S треугольника, если известны его стороны a, b и c и радиус R окружности, описанной около треугольника.
Запишите формулу для нахождения радиуса R окружности, описанной около треугольника, если известны его стороны a, b и c и площадь S.
Запишите формулу для вычисления площади S треугольника, если известны его полупериметр p и радиус r окружности, вписанной в треугольник.
Запишите формулу для нахождения радиуса r окружности, вписанной в треугольник, если известны площадь S треугольника и его полупериметр p.
Вычислите площадь треугольника, две стороны которого равны 5 см и 4 см, а угол между ними равен 150°.
Площадь остроугольного треугольника ABC равна 3 см 2 , AB = 2 см, BC = 2 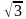
Чему равен радиус окружности, вписанной в треугольник, площадь которого равна
36 см 2 , а периметр — 18 см?
Радиус окружности, описанной около треугольника, равен 4 см, а произведение сторон треугольника — 80 см 3 . Чему равна площадь треугольника?
Чему равна площадь ромба, сторона которого равна 8 см, а один из углов — 60°?
Радиус окружности, описанной около прямоугольника, равен 3 см, а угол между диагоналями — 45°. Чему равна площадь прямоугольника?
Чему равна площадь выпуклого четырёхугольника, диагонали которого равны 7 см и 8 см, а угол между ними равен 30°?
Диктант 5 по теме «Правильные многоугольники и их свойства»
Запишите окончание предложения:
1) многоугольник называют правильным, если у него … ;
2) любой правильный многоугольник является одновременно вписанным в окружность и … ;
3) центры вписанной и описанной окружностей правильного многоугольника … ;
4) центром правильного многоугольника называют точку, которая является … ;
5) каждый угол правильного n-угольника равен … ;
6) центральный угол правильного n-угольника равен … ;
7) радиус описанной окружности правильного n-угольника можно вычислить по формуле …;
8) радиус вписанной окружности правильного n-угольника можно вычислить по формуле … .
Какую наибольшую градусную меру может иметь центральный угол правильного многоугольника? Сколько сторон имеет этот многоугольник?
Сторона правильного треугольника равна a. Запишите формулу для нахождения радиуса:
1) описанной окружности треугольника;
2) его вписанной окружности.
Сторона правильного четырёхугольника равна a. Запишите формулу для нахождения радиуса:
1) описанной окружности четырёхугольника;
2) его вписанной окружности.
Сторона правильного шестиугольника равна a. Запишите формулу для нахождения радиуса:
1) описанной окружности шестиугольника;
2) его вписанной окружности.
Верно ли утверждение: если в треугольнике все углы равны, то он является правильным? Ответ обоснуйте.
Верно ли утверждение: если в четырёхугольнике все углы равны, то он является правильным? Ответ обоснуйте.
Верно ли утверждение: если в треугольнике все стороны равны, то он является правильным? Ответ обоснуйте.
Верно ли утверждение: если в четырёхугольнике все стороны равны, то он является правильным? Ответ обоснуйте.
Могут ли биссектрисы углов правильного многоугольника и серединные перпендикуляры его сторон пересекаться в двух разных точках? Ответ обоснуйте.
Сколько углов имеет правильный многоугольник, у которого радиус описанной окружности вдвое больше радиуса вписанной окружности?
Сколько углов имеет правильный многоугольник, у которого радиус описанной окружности равен стороне многоугольника?
Сколько углов имеет правильный многоугольник, у которого радиус вписанной окружности вдвое меньше стороны многоугольника?
Диктант 6 по теме «Длина окружности. Площадь круга»
Запишите окончание предложения:
1) греческой буквой π принято обозначать число, равное отношению … ;
2) каждую из двух частей круга, на которые делят его два радиуса, вместе с этими радиусами называют … ;
3) каждую из двух частей круга, на которые делит круг его хорда, вместе с этой хордой называют … .
Запишите формулу для вычисления длины C окружности, радиус которой равен R.
Запишите формулу для вычисления длины l дуги окружности, градусная мера которой равна n°, если радиус окружности равен R.
Запишите формулу для вычисления площади S круга, радиус которого равен R.
Запишите формулу для вычисления площади S сектора, содержащего дугу окружности, градусная мера которой равна n°, если радиус круга равен R.
Длина окружности равна 36π см. Чему равен радиус окружности?
Площадь круга равна 49π см 2 . Чему равна длина окружности, его ограничивающей?
Чему равна длина дуги окружности, градусная мера которой равна 20°, если радиус окружности равен 27 см?
Радиус круга равен 2 см. Найдите площадь сектора, градусная мера дуги которого равна 270°.
Как изменится длина окружности, если её:
1) радиус увеличить в 4 раза;
2) диаметр уменьшить в 10 раз?
Как изменится площадь круга, если его:
1) радиус увеличить в 4 раза;
2) диаметр уменьшить в 10 раз?
Как надо изменить радиус круга, чтобы его площадь увеличилась в 2 раза?
Круговой сектор содержит дугу, градусная мера которой равна α. Чему равно α, если площадь сектора составляет:
1) треть площади круга;
2) половину площади круга;
3) 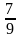
Диктант 7 по теме «Расстояние между двумя точками с заданными координатами. Координаты середины отрезка»
Запишите формулу, по которой находят расстояние между точками A (x1; y1) и
B (x2; y2) координатной плоскости.
Запишите формулу, по которой находят координаты (x0; y0) середины отрезка AB, если A (x1; y1) и B (x2; y2).
Вычислите длину отрезка MK, если M (2; −1) и K (1; 2).
Чему равно расстояние от точки M (−6; 9) до:
1) оси абсцисс; 2) оси ординат?
Чему равно расстояние от начала координат до точки:
Найдите координаты середины отрезка CD, если C (−2; 4) и D (2; −6).
Запишите координаты центра окружности, если концами её диаметра являются точки (−1; 4) и (9; −2).
Является ли параллелограммом четырёхугольник ABCD, если A (−8; −5), B (−6; 3), C (6; 7), D (4; −2)?
Середина отрезка AB лежит на оси абсцисс. Укажите ординату точки B, если ордината точки A равна 8.
Диктант 8 по теме «Уравнение фигуры. Уравнение окружности»
Запишите окончание предложения:
1) уравнением фигуры F, заданной на плоскости xy, называют уравнение с двумя переменными x и y, имеющее такие свойства: … ;
2) уравнение окружности радиусом R с центром в точке A (a; b) имеет вид … ;
3) любое уравнение вида (x − a) 2 + (y − b) 2 = R 2 , где R 0, является уравнением… ;
4) уравнение окружности радиусом R с центром в начале координат имеет вид … .
Дана окружность (x − 8) 2 + (y + 14) 2 = 81. Запишите:
1) чему равен радиус данной окружности;
2) координаты центра окружности.
Запишите уравнение окружности радиусом 9 с центром в точке (−2; 3).
Запишите уравнение окружности с центром в точке (−5; 6), касающейся:
1) оси абсцисс; 2) оси ординат.
Дана окружность радиусом 5 с центром в начале координат.
1) Сколько точек пересечения имеет эта окружность с осями координат?
2) Запишите координаты точек пересечения этой окружности с осями координат.
Запишите уравнения окружностей, центры которых принадлежат оси ординат, касающихся оси абсцисс и радиус которых равен 1.
Запишите все значения b, при которых окружность (x − 4) 2 + (y − b) 2 = 49 касается оси абсцисс.
Какому наименьшему натуральному числу должен быть равен радиус окружности с центром в точке A (−4; 8), чтобы эта окружность пересекала ось ординат?
Какому наибольшему натуральному числу должен быть равен радиус окружности с центром в точке B (−9; −12), чтобы эта окружность не имела общих точек с осью абсцисс?
Диктант 9 по теме «Уравнение прямой. Угловой коэффициент прямой»
Запишите окончание предложения:
1) уравнение прямой имеет вид … ;
2) уравнение прямой является частным видом … ;
3) если b = 0 и a ≠ 0, то уравнение прямой ax + by = c задаёт … ;
4) если b ≠ 0, то уравнение прямой ax + by = c задаёт … ;
5) уравнение невертикальной прямой удобно записывать в виде … ;
6) если прямая задана уравнением y = kx + p, то коэффициент k называют … ;
7) если невертикальная прямая образует с положительным направлением оси абсцисс угол α, то угловой коэффициент прямой равен … ;
Запишите уравнение прямой, которая проходит через точку M (−1; 8) и:
1) параллельна оси абсцисс;
2) перпендикулярна оси абсцисс;
3) проходит через начало координат.
Прямая проходит через точки A (5; 0) и B (5; 3). Проходит ли эта прямая через точку:
Является ли уравнение 6 + 2y = 0 уравнением прямой?
Как расположена относительно осей координат прямая 7x − 3 = 0?
Запишите координаты точки пересечения прямой 9x − 2y = 18:
1) с осью абсцисс; 2) с осью ординат.
Чему равен угловой коэффициент прямой:
Запишите уравнение какой-либо прямой:
1) угловой коэффициент которой равен 1;
2) угловой коэффициент которой равен 0;
3) угловой коэффициент которой не определён;
4) образующей с положительным направлением оси абсцисс угол 30°.
Запишите уравнение прямой, проходящей через точку (0; −17), угловой коэффициент которой равен −6.
Дана прямая y = 7x − 5. Запишите уравнение какой-либо прямой, которая:
1) параллельна данной прямой;
2) пересекает данную прямую.
Каково взаимное расположение окружности x 2 + y 2 = 64 и прямой:
Диктант 10 по теме «Понятие вектора»
Запишите окончание предложения:
1) величины, которые определяются не только числовым значением, но и направлением, называют … ;
2) отрезок называют направленным отрезком или вектором, если указано … ;
3) вектор с началом в точке M и концом в точке K обозначают так: … ;
4) нулевым вектором или нуль-вектором называют вектор, у которого … ;
5) нулевой вектор обозначают так: … ;
6) модулем вектора 
7) модуль нулевого вектора считают равным … ;
8) ненулевые векторы называют коллинеарными, если они … ;
9) нулевой вектор считают коллинеарным … ;
10) тот факт, что векторы 

11) если векторы 

12) если векторы 

13) если 


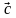
14) если 


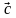
15) ненулевые векторы называют равными, если … .
Начертите два вектора:
1) имеющие равные модули и неколлинеарные;
2) имеющие равные модули и сонаправленные;
3) имеющие равные модули и противоположно направленные.
Начертите параллелограмм ABCD. Через точку пересечения его диагоналей проведите прямую, пересекающую сторону AD в точке M, а сторону BC — в точке K. Рассмотрите векторы 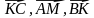
1) коллинеарных векторов;
2) сонаправленных векторов;
3) противоположно направленных векторов;
4) векторов, имеющих равные модули;
5) равных векторов.
Даны две точки A и B. Верно ли утверждение:
1) модуль вектора 
2) векторы 
Точка C — середина отрезка AB. Верно ли утверждение:
1) векторы и равны;
2) векторы и равны?
Начертите треугольник ABC, отложите:
1) от вершины A вектор, равный вектору ;
2) от вершины A вектор, равный вектору ;
3) от вершины C вектор, равный вектору 
Диктант 11 по теме «Координаты вектора»
Запишите окончание предложения:
1) у равных векторов соответствующие координаты … ;
2) если соответствующие координаты векторов равны, то … ;
3) нулевой вектор имеет координаты … ;
4) если точки A (x1; y1) и B (x2; y2) соответственно являются началом и концом вектора 

5) если вектор 
От точки O — начала координат — отложили вектор . Точка A имеет координаты (9; −6). Запишите координаты вектора .
Отметьте на координатной плоскости точку M (1; 4). Отложите от точки M векторы (2; −3) и (3; −5). Запишите координаты точек A и B.
Найдите модуль вектора , если:
Найдите координаты вектора , если B (−1; 2), C (7; 4).
Диктант 12 по теме «Сложение и вычитание векторов»
Запишите окончание предложения:
1) для любых трёх точек A, B и C выполняется равенство 
2) если координаты векторов 



3) разностью векторов 

4) для любых трёх точек O, A и B выполняется равенство − = . ;
5) если координаты векторов 



6) два ненулевых вектора называют противоположными, если … ;
7) вектором, противоположным нулевому вектору, считают … ;
8) если вектор 

Может ли сумма двух векторов быть равной нулевому вектору? Ответ обоснуйте.
Может ли сумма двух векторов быть равной одному из слагаемых? Ответ обоснуйте.
Может ли модуль суммы двух векторов быть равным сумме модулей этих векторов? Ответ обоснуйте.
Начертите произвольный треугольник DEF.
1) Постройте вектор , равный сумме векторов и .
2) Найдите сумму векторов и .
3) Постройте вектор , равный разности векторов и .
Запишите выражение: 
Каковы координаты вектора, равного сумме векторов (−3; 10) и (−2; −7)?
Каковы координаты вектора, равного разности векторов 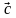
Каково расположение точек A, B, C, если векторы 
Запишите вектор 
Запишите вектор 
Диктант 13 по теме «Умножение вектора на число»
Запишите окончание предложения:
1) произведением ненулевого вектора 

2) если 

3) если векторы 


4) если вектор 

Запишите сочетательное свойство умножения вектора на число.
Запишите первое распределительное свойство умножения вектора на число.
Запишите второе распределительное свойство умножения вектора на число.
Изобразите произвольный вектор 


Во сколько раз модуль вектора −4 

Даны ненулевой вектор 
1) векторы 3 

2) векторы −5 

3) векторы k 

На какое число надо умножить вектор 

Какие координаты имеет вектор 



Координаты вектора равны (1; 5), а координаты коллинеарного ему вектора равны (−4; y). Чему равен y?
Диктант 14 по теме «Скалярное произведение векторов»
Запишите окончание предложения:
1) скалярным произведением двух векторов называют … ;
2) скалярным квадратом вектора 
3) скалярный квадрат вектора равен … ;
4) скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда … ;
5) скалярное произведение векторов 

6) косинус угла между векторами 

формуле … .
Известно, что угол между векторами 

1) 3 


2) −2 



Найдите скалярное произведение векторов 

1) = 2, ∠ 60°; 2) = 1, ∠ =135°.
Острый или тупой угол образуют векторы:
1) 



3) 

Перпендикулярны ли векторы:
1) 



Может ли скалярное произведение векторов быть равным произведению их модулей? Если ответ утвердительный, то объясните, в каком это будет случае.
Известно, что для ненулевых векторов 





Чему равно скалярное произведение векторов 

Может ли скалярное произведение двух неперпендикулярных векторов быть равным нулю? Ответ обоснуйте.
Диктант 15 по теме «Движение (перемещение) фигуры. Параллельный перенос»
Запишите окончание предложения:
1) преобразование фигуры F, сохраняющее расстояние между точками, называют … ;
2) образом прямой при движении является … ;
3) образом отрезка при движении является … ;
4) образом угла при движении является … ;
5) образом треугольника при движении является … ;
6) две фигуры называют равными, если … .
Может ли при движении:
1) образом стороны параллелограмма быть его сторона, противоположная данной;
2) образом боковой стороны прямоугольной трапеции быть её другая боковая сторона;
3) образом основания трапеции быть её другое основание;
4) образом диагонали квадрата быть её другая диагональ;
5) образом одного из углов разностороннего треугольника быть один из двух других его углов;
6) образом одного из углов равностороннего треугольника быть один из двух других его углов?
Образом равнобедренного прямоугольного треугольника ABC с гипотенузой AB при движении является треугольник A1B1C1. Запишите величины углов треугольника A1B1C1.
Начертите треугольник ABC. Постройте образ треугольника ABC при параллельном переносе: 1) на вектор ; 2) на вектор 2 .
Начертите параллелограмм ABCD. Постройте образ параллелограмма ABCD при параллельном переносе: 1) на вектор ; 2) на вектор .
При каком условии образом точки при двух последовательно выполненных параллельных переносах будет сама эта точка?
Образом начала координат при параллельном переносе на вектор 
Образом точки B при параллельном переносе на вектор 
C (4; 4). Запишите координаты точки B.
Каково взаимное расположение прямой a и её образа при параллельном переносе, если образом точки A, принадлежащей прямой a, является точка B, которая:
1) не принадлежит прямой a;
2) принадлежит прямой a?
Каким условиям должны удовлетворять два отрезка, чтобы один из них был образом другого отрезка при параллельном переносе?
Каким условиям должны удовлетворять две окружности, чтобы одна из них была образом другой окружности при параллельном переносе?
Диктант 16 по теме «Осевая симметрия»
Запишите окончание предложения:
1) точки A и A1 называют симметричными относительно прямой l, если … ;
2) если точка A принадлежит прямой l, то точкой, симметричной ей относительно прямой l, считают … ;
3) если две фигуры симметричны относительно прямой, то они … ;
4) фигуру называют симметричной относительно прямой l, если … .
Начертите незамкнутую ломаную ABCD и проведите прямую a, не пересекающую её. Постройте ломаную, симметричную ломаной ABCD относительно прямой a. Обозначьте полученную ломаную. Запишите пары звеньев ломаной, симметричных относительно прямой a.
Начертите прямоугольник, отличный от квадрата. Постройте образ этого прямоугольника при симметрии относительно прямой, содержащей одну из его диагоналей.
Начертите прямоугольную трапецию. Постройте образ этой трапеции при симметрии относительно прямой, содержащей её:
1) меньшую боковую сторону; 2) бóльшую боковую сторону.
Сколько осей симметрии имеет:
1) правильный пятиугольник;
2) правильный шестиугольник;
3) фигура, состоящая из двух перпендикулярных прямых;
4) фигура, состоящая из двух параллельных прямых?
В каком случае образом точки при осевой симметрии является сама эта точка?
Начертите выпуклый четырёхугольник ABCD, имеющий одну ось симметрии — прямую BD.
Начертите четырёхугольник ABCD, не являющийся выпуклым и имеющий одну ось симметрии — прямую BD.
Запишите окончание предложения:
1) две точки с равными ординатами и противоположными абсциссами симметричны относительно … ;
2) две точки с равными абсциссами и противоположными ординатами симметричны относительно … ;
3) точки A (4; −6) и B (4; 6) симметричны относительно … ;
4) точки C (−5; 8) и D (5; 8) симметричны относительно … ;
5) образом прямой y = 20 при симметрии относительно оси абсцисс является
прямая … ;
6) образом прямой x = −12 при симметрии относительно оси ординат является
прямая … .
Диктант 17 по теме «Центральная симметрия. Поворот»
Запишите окончание предложения:
1) точки A и A1 называют симметричными относительно точки O, если … ;
2) если две фигуры симметричны относительно точки, то они … ;
3) фигуру называют симметричной относительно точки O, если … .
Начертите незамкнутую ломаную ABCD и отметьте точку O, не принадлежащую ей. Постройте ломаную, симметричную ломаной ABCD относительно точки O. Обозначьте полученную ломаную. Запишите пары звеньев ломаной, симметричных относительно точки O.
Начертите произвольную трапецию и постройте её образ при симметрии относительно точки пересечения диагоналей данной трапеции.
Какая фигура является образом:
1) луча AB при симметрии относительно центра A;
2) угла ABC при симметрии относительно центра B?
В каком случае образом точки при центральной симметрии является эта же точка?
В каком случае образом прямой при центральной симметрии является эта же прямая?
Какие правильные многоугольники имеют центр симметрии?
Точка B симметрична точке A относительно точки O. Запишите это утверждение с помощью векторов.
Какая фигура является образом треугольника ABC в результате двух последовательно выполненных центральных симметрий относительно одной и той же точки?
Запишите координаты точки, симметричной точке A (−10; 18) относительно начала координат.
Запишите координаты точки, относительно которой симметричны точки A (24; 0) и
B (0; −30).
Запишите уравнение прямой, симметричной прямой y = 6 относительно:
1) начала координат; 2) точки (2; −5).
Приведите пример фигуры:
1) не имеющей ни центра симметрии, ни оси симметрии;
2) имеющей центр симметрии, но не имеющей оси симметрии;
3) имеющей ось симметрии, но не имеющей центра симметрии;
4) имеющей центр симметрии и хотя бы одну ось симметрии;
5) имеющей бесконечно много центров и осей симметрии.
Начертите отрезок AB. Постройте образ этого отрезка при повороте:
1) вокруг точки A на угол 70° по часовой стрелке;
2) вокруг точки B на угол 100° против часовой стрелки;
3) вокруг середины отрезка AB на угол 60° по часовой стрелке.
Где должен быть расположен центр поворота и чему должен быть равен угол поворота, при котором:
1) образом прямой является эта же прямая;
2) образом отрезка является этот же отрезок;
3) образом окружности является эта же окружность;
4) образом квадрата является этот же квадрат;
5) образом правильного треугольника является этот же треугольник;
6) образом прямого угла является угол, смежный с данным углом?
16. Запишите координаты точки, являющейся образом точки A (−3; 0) при повороте вокруг начала координат на угол 90°:
1) по часовой стрелке; 2) против часовой стрелки.
17. Запишите координаты точки, являющейся образом точки A (−4; 4) при повороте вокруг начала координат на угол 90°:
1) по часовой стрелке; 2) против часовой стрелки.
Диктант 18 по теме «Гомотетия. Подобие фигур»
Запишите окончание предложения:
1) точка X1 — образ точки X при гомотетии с центром O и коэффициентом k, если … ;
2) гомотетия является центральной симметрией относительно точки O, если коэффициент гомотетии равен … ;
3) гомотетия является тождественным преобразованием, если коэффициент гомотетии равен … ;
4) гомотетия не является движением, если коэффициент гомотетии … ;
5) при гомотетии фигуры F с коэффициентом k все расстояния между её точками … ;
6) образом прямой при гомотетии является … ;
7) образом угла при гомотетии является … ;
8) две фигуры называют подобными, если … ;
9) при преобразовании подобия фигуры F расстояния между её точками … ;
10) отношение площадей подобных многоугольников равно … .
В результате гомотетии с центром A образом точки B является точка B1. Чему равен коэффициент гомотетии, если AB = 15 см, AB1 = 20 см?
В каком случае образом прямой при гомотетии является сама эта прямая?
Верно ли утверждение: если отрезок A1B1 — образ отрезка AB при гомотетии, то отрезки AB и A1B1 параллельны?
Могут ли два ромба, имеющие общий угол, быть гомотетичными? В случае утвердительного ответа укажите, где должен располагаться центр гомотетии.
Сторона первого квадрата в 3 раза меньше стороны второго квадрата. Какова площадь первого квадрата, если площадь второго квадрата равна 45 см 2 ?
Во сколько раз надо уменьшить сторону квадрата, чтобы его площадь уменьшилась в 2 раза?
Площади двух подобных параллелограммов относятся как a : b. Чему равно отношение их периметров?
Как относятся площади двух равносторонних треугольников, если их стороны относятся как 2 : 7?
На карте, масштаб которой равен 1 : 100, площадь земельного участка равна 15 см 2 . Какова площадь этого участка на местности?
Диктант 19 по теме «Прямая призма. Пирамида»
Изобразите прямую призму Укажите:
рёбра, выходящие из вершины ;
рёбра нижнего основания призмы;
боковые грани, которым принадлежит точка ;
вершины основания, не принадлежащие боковой грани .
Изобразите пирамиду OABCD. Укажите:
боковые грани, которым принадлежит точка С;
рёбра основания пирамиды;
вершины основания, не принадлежащие боковой грани OCD;
вершины основания, не принадлежащие боковой грани ОВС.
Запишите формулу, по которой вычисляют объём прямой призмы.
Запишите формулу, по которой вычисляют объём пирамиды.
Диктант 20 по теме «Цилиндр. Конус. Шар»
Изобразите цилиндр. Проведите в нём:
Запишите формулу, по которой вычисляют площадь боковой поверхности цилиндра.
Запишите формулу, по которой вычисляют объём цилиндра.
Изобразите конус. Проведите в нём:
Запишите формулу, по которой вычисляют площадь боковой поверхности конуса.
Запишите формулу, по которой вычисляют объём конуса.
Запишите формулу, по которой вычисляют площадь поверхности шара.
Радиус основания цилиндра равен 1 см, а его образующая – 4 см. Найдите площадь боковой поверхности цилиндра.
Найдите объём конуса, высота которого равна 2 см, а радиус основания – 4 см.
Как изменятся площадь и объём шара, если его радиус увеличить в 6 раз?
🎦 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Видеоурок "Общие уравнения прямой"Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение параллельной прямойСкачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Прямая и уравнение прямойСкачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать