Уравнение нестационарной теплопроводности твердых тел (8 видео)

Решение задач нестационарной теплопроводности.

НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ.

Общие положения. Описание процесса.

Ранее были рассмотрены условия распространения теплоты при стационарном режиме, когда температурное поле не менялось во времени, оставалось постоянным.

Если же температурное поле меняется во времени, т.е. является функцией времени, то протекающие в таких условия процессы называются нестационарными.

Нестационарные процессы теплопроводности встречаются при охлаждении и нагреве металлических заготовок, прокалывании твердых тел, в производстве стекла, обжига кирпича и т.д.

В качестве примера рассмотрим такой случай. Тело внесено в среду более высокой температурой; сразу же между средой и телом возникает процесс теплообмена, и тело начинает прогреваться. Сначала нагреваются поверхностные слои, но постепенно процесс прогрева распространяется вглубь тела (рис. 1.6.1).

По истечении некоторого времени (теоретически бесконечно большого) температура всех частей тела выравнивается и становится равной температуре окружающей среды, т.е. наступает тепловое равновесие.

На рис. 1.6.1 показан характер кривых, полученных при нагревании однородного твердого тела в среде с постоянной температурой .По мере нагрева температура в каждой точке асимптотически приближается к температуре нагревающей среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела. С увеличением времени прогрева эта разность будет уменьшаться и теоретически через достаточно большой отрезок времени она будет равна нулю.

При нестационарном режиме количество переданной теплоты также непостоянно во времени (рис. 1.6.2). По мере прогрева тела количество воспринимаемой теплоты уменьшается и в пределе становится равным нулю. Площадь, заключенная между осями и кривой, определяет собой полное количество теплоты, переданное за время . Эта теплота аккумулируется телом. Нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества.

Аналогичным образом протекает и процесс охлаждения тела, при этом выделенная теплота передается в окружающую среду.

Скорость теплового процесса при нестационарном режиме определяется значением коэффициента температуропроводности

а , .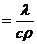

Любой процесс нагревания или охлаждения тела можно разделить на три режима.

Первый режим — начало процесса.

Характерной особенностью этого режима является распространение температурных возмущений в пространстве и захват все новых и новых слоев тела. Скорость изменения температуры в отдельных точках при этом режиме различна и зависит от начальных условий.

Это режим неупорядоченного процесса.

С течением времени скорость изменения температуры во всех точках тела становится постоянной. Это режим упорядоченного процесса, он называется регулярным режимом.

По прошествии длительного времени наступает третий режим, характерной особенностью которого является постоянство распределения температур во времени – это стационарный режим.

Например, в работе паровых котлов нестационарный режим возникает лишь при пуске в работу, выключении и изменении режима работы и имеет временный характер. Поэтому расчет таких аппаратов производится лишь для основного, стационарного режима, а для нестационарного совсем не рассчитывается. В работе же нагревательных печей, наоборот, нестационарный режим является основным, при их расчете приходится определять время, необходимое для прогрева металла до заданной температуры, или температуру, до которой металл нагреется в течение определенного промежутка времени.

Описанный характер изменения температуры и количества переданной теплоты справедливы лишь для твердых тел.

Решение задач нестационарной теплопроводности.

Решить задачу нестационарной теплопроводности это значит найти зависимость изменения температуры и количество теплоты переданной телу во времени для любой точки тела:

Для аналитического нахождения этих зависимостей может быть использовано дифференциальное уравнение теплопроводности Фурье:

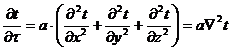
Это уравнение решается с помощью рядов Фурье. Аналитическое решение получается очень сложным и возможно лишь для тел простой формы (пластины, цилиндра и шара) при целом ряде упрощающих предпосылок.

Аналитическое описание процесса теплопроводности кроме дифференциального уравнения также включает в себя и условия однозначности.

Условия однозначности задаются в виде:

· физических параметров , , ;

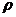
· формы и геометрических размеров объекта ;

· температуры тела в начальный момент времени 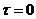; t = t₀ = f(x, у, z).

· граничных условий, которые могут быть заданы в виде граничных условий третьего рода:

Дифференциальное уравнение теплопроводности совместно с условиями однозначности дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции, которая удовлетворяла бы уравнению и условиям однозначности.

t=f(x,y,z,i,a,t₀,t_ж, )

Если решить это уравнение для плоской стенки и рассмотреть процесс изменения температуры только в одном направлении x, то решение будет иметь следующий вид:

где b иcопределяются из условий стационарности процесса, т.е. при ;

, — из граничных условий 3 рода;

— из начальных условий, т.е. при .

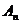
Из уравнения видно, что искомая функция t зависит от большого числа переменных, которые можно сгруппировать в 3 безразмерных комплекса, эти комплексы называются числами подобия.

Первое число подобия — Число Био:

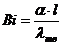
где — коэффициент теплоотдачи на границе жидкости и твердого тела;

λ — коэффициент теплопроводности твердого тела;

l— характеристический размер, который определяется в зависимости от формы тела:

для пластины l=δ;

для цилиндра l= ;

для шара l= .

Второе число подобия — Число Фурье:

гдеa— коэффициент температуропроводности;

Число Фурье называют также безразмерным временем.

Третий безразмерный комплекс — безразмерная координата:

Установлено, что θ— безразмерная температура, является функцией чисел Био и Фурье, для фиксированных значений , т.е.

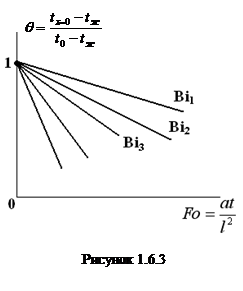
Изменение безразмерной температуры θ для центра ( 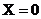) и поверхности ( ) можно представить графическим решением, которое приведено на рисунке 1.6.3.

Уравнение нестационарной теплопроводности твердых тел

Подобные графики построены для центра и поверхности пластины, цилиндра и шара, а так же для безразмерного количества теплоты, которая является функцией числа Bi и :

Следовательно, чтобы определить температуру на поверхности или в центре тела необходимо знать две величины: число Bi и число .

Таким образом, метод решения задач нестационарной теплопроводности заключается в следующем:

1) задаются геометрическими, начальными и граничными условиями [(с;λ; ; ;α; ),( или )];

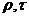
2) вычисляют числа Bi и ;

, ;

3) зная числа Bi и по графику, определяют безразмерную температуру θ;

4) определив θ, рассчитывают температуру в центре

или на поверхности тела

где — начальная температура тела;

— температура среды.

Рассмотрим влияние значений чисел Bi на распределение температуры в теле на примере охлаждения пластины.

Из полученного решения следует, что для любого момента времени температурное поле имеет вид симметричной кривой с максимумом на оси пластины ( ). В каждый последующий момент будет своя кривая, монотонно убывающая к поверхности (рис. 1.6.4).

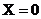
Для любого момента времени касательные к кривым в точках проходят через направляющие точки +А и

– А, которые расположены на расстоянии от поверхности пластины, причем

или ,

отсюда , т.е. расстояние до точки А полностью определяется условиями однозначности.

Сказанное справедливо для всех поверхностей.

Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

Электронная библиотека

Для определения количества теплоты, проходящей за время через изотермическую поверхность твердого тела конечных размеров, необходимо проинтегрировать уравнение, отражающее закон Фурье, по и , т.е. необходимо знать температурное поле внутри рассматриваемого тела и знать, как оно изменяется с течением времени.

Для решения этой задачи выводится дифференциальное уравнение теплопроводности при следующих допущениях: тело однородное, физические параметры его постоянны. В соответствии с законом сохранения энергии количество теплоты ( ), введенное в элементарный объем за время путем теплопроводности, плюс количество теплоты, выделяемое внутренними источниками , должно быть равно изменению внутренней энергии вещества ( ):

Для определения членов этого уравнения в декартовой системе координат выделим в теле элементарный параллелепипед со сторонами (рис. 10.4). Подводимую теплоту обозначим через , а отводимую – .

10.4. Схема для вывода дифференциального уравнения энергии

Тогда для грани из закона Фурье найдем:

Разность величин представляет собой количество теплоты, остающейся в параллелепипеде:

Аналогичные зависимости получаются для двух других граней:

Тогда общее количество теплоты, оставшееся в теле, равно:

Если обозначить через удельную теплопроизводительность внутренних источников тепла, то можно записать:

Изменение внутренней энергии тела за время составляет:

Таким образом, окончательно получим:

Введем обозначение: – коэффициент температуропроводности, который характеризует степень нестационарности режима. Подставим его в последнее уравнение, получим:

Таким образом, получено уравнение, связывающее временное и пространственное изменения температуры в любой точке тела.

Видео:Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Нестационарная теплопроводность. Основные уравнения

Двигатели внутреннего сгорания, компрессоры и автоматическое оружие периодически выделяют тепло. Это рассеивание тепла вызывает периодические изменения температуры окружающих объектов. Другим примером является влияние ежедневных изменений температуры на крупные сооружения, такие как мосты, и на мелкие объекты, такие как рост растений. Главным дифференциальным уравнением нестационарной теплопроводности в твердых телах является частный случай дифференциального уравнения энергии. 10.It также применяется к стационарным несжимаемым жидкостям. Если теплопроводность постоянна и отсутствует тепловыделение, то уравнение энергии.

Описывается следующим образом: x / 94 I dH | dc dx-cCp dx2 ′ dy2 ’dg2)’ среди конкретных случаев, на которые следует ориентироваться, существует нестационарная теплопроводность только одного направления, и Формула(10. Двенадцать) д * ДСР ДХ ’ДХ *’ 21. *） Для стационарной теплопроводности,= 0, и Формула(10. 12) принимает форму: 4 — = 0 ЦОР * » ду * ДГ * (21.2） Уравнение установившейся теплопроводности в одном измерении(10. 12) написать и、 Это уравнение легко интегрируется и показывает линейную зависимость между температурой и расстоянием. Ранее эта зависимость формировалась в результате интегрирования закона теплопроводности fouv по формуле (20. 3) был получен В.

Дифференциальные уравнения энергии также могут быть получены в цилиндрических координатах путем учета энергетического баланса контролируемых объемов в виде полого цилиндра. Если нет движения и лихорадки, уравнение Д1 _ а, КСО, ЦОР (21. Три） (Б. 1 Н1, 1 9 * 1, г * 1 ДГ * г ДГ г * ’ДЦ> * ДГ *)’ если теплопроводность в направлении z пренебрежимо мала= 0, если температура не изменяется в зависимости от угла, то 0.Формула(21. 3) выведение、 Body.

Во многих технических задачах мы сталкиваемся с цилиндрическими телами и уравнениями(21. 3) и его упрощенной формой является уравнение, описанное в декартовых координатах(10. 12) более полезным. Пример 21. Один ppml3a. если lead1 выравнивает записанную энергию в сферических координатах, нагрев или охлаждение сферы может быть легко разрешено. Случай «анализ к0хаа высокий, температура не зависит от значения угла температуры, выбирает центр sphere.

Расстояние r от центра, tu / сферического при постоянной температуре равно 110VARCHY0ST’.Расстояние от центра R находится в dr, объем равен Рм? Surfaces1 2 поверхности вышли из-под контроля * Тепловой поток в управляющем объеме равен — Х(4lg») А. (1)тепловой поток от блока управления равен — Х [4л(р + ^ р) 2] = = — W [r » 4-2rg +(4r）*）（-^-±| ^ Р -). (2） Полученный тепловой поток получается вычитанием (1) из (2).После этого вы можете игнорировать термины 2-го и 3-го порядка (потому что они незначительны).Результирующий тепловой поток будет равен 4x(r2’y — * + 2r4g / g)-(3). Скорость накопления энергии контролируемого объема (4lg2 ДГ) КСО（*). Она равна тепловому потоку к полученному volume.