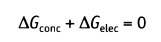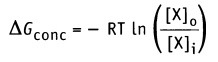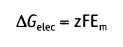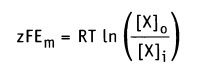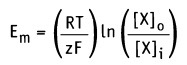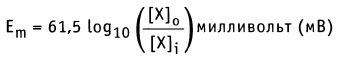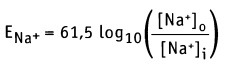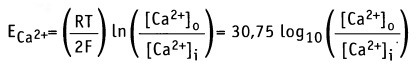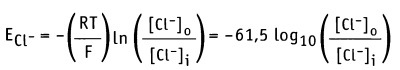Видео:011 Электрохимия 4 уравнение НернстаСкачать
Применение уравнения Нернста в решении задач.
При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:
Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:
Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.
Пример 1:
Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO4 и 0.01М ZnSO4 соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.
Решение:
Для начала запишем уравнения протекающих процессов:
Далее находим по таблице стандартные потенциалы процессов:
Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.
Найдем реальные потенциалы с учетом нестандартных активностей ионов:
Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:
Ответ: 1.13 В
Пример 2:
Одним из лабораторных способов получения хлора является действие KMnO4 на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?
Решение:
Для начала запишем уравнения протекающих процессов.
Далее находим по таблице стандартные потенциалы процессов:
Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:
Получается, что потенциал KMnO4 стал меньше, чем у хлора, а значит, реакция не пойдет.
Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать
Напишите уравнение Нернста и укажите каково его значение
где Е — потенциал;
R — универсальная газовая постоянная, т.е кинетическая энергия 1 моля ионов при абсолютной температуре, равной 1о по Кельвину;
Т — абсолютная температура; n — валентность иона;
F — число Фарадея (заряд 1 моля одновалентных ионов);
Cнар. — концентрация ионов снаружи мембраны;
Свн. — концентрация ионов внутри клетки.
Уравнение Нернста — уравнение, связывающее окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, и стандартными электродными потенциалами окислительно-восстановительных пар.
Нернст изучал поведение электролитов при пропускании электрического тока и открыл закон. Закон устанавливает зависимость между электродвижущей силой ( разностью потенциалов ) и ионной концентрацией. Уравнение Нернста позволяет предсказать максимальный рабочий потенциал, который может быть получен в результате электрохимического взаимодействия, когда известны давление и температура. Таким образом, этот закон связывает термодинамику с электрохимической теорией в области решения проблем, касающихся сильно разбавленных растворов. E=E0+RTnFlnaOxaRed,
· E — электродный потенциал, E0 — стандартный электродный потенциал, измеряется в вольтах;
· R — универсальная газовая постоянная, равная 8.31 Дж/(моль·K);
· T — абсолютная температура;
· F — постоянная Фарадея, равная 96485,35 Кл·моль −1 ;
· n — число молей электронов, участвующих в процессе;
· aOx и aRed — активности соответственно окисленной и восстановленной форм вещества, участвующего в полуреакции.
Если в формулу Нернста подставить числовые значения констант R и F и перейти от натуральных логарифмов к десятичным, то при T=298K получим
Опишите механизм возникновения потенциала действия.
Следовая гиперполяризация
Потенциал-зависимые натриевые каналы
Фазы потенциала действия
1. Предспайк — процесс медленной деполяризации мембраны до критического уровня деполяризации (местное возбуждение, локальный ответ).
2. Пиковый потенциал, или спайк, состоящий из восходящей части (деполяризация мембраны) и нисходящей части (реполяризация мембраны).
3. Отрицательный следовой потенциал — от критического уровня деполяризации до исходного уровня поляризации мембраны (следовая деполяризация).
4. Положительный следовой потенциал — увеличение мембранного потенциала и постепенное возвращение его к исходной величине (следовая гиперполяризация).
Фазы
ЛО- локальный ответ
МПП-мембранный потенциал 
13. что такое деполяризация и каковы ее механизмы?
Уменьшение МП относительно его нормального уровня (ПП) называют деполяризацией
Фаза деполяризации. Развитие ПД возможно только при действии раздражителей, которые вызывают деполяризацию клеточной мембраны. При деполяризации клеточной мембраны до критического уровня деполяризации (КУД) происходит лавинообразное открытие потенциалчувствительных Na+-каналов. Положительно заряженные ионы Na+ входят в клетку по градиенту концентрации (натриевый ток), в результате чего мембранный потенциал очень быстро уменьшается до 0, а затем приобретает положительное значение. Явление изменения знака мембранного потенциала называют реверсией заряда мембраны.
Рис. 2.4. Изменение мембран-ного потенциала, интенсивности калиевого и натриевого трансмембранного тока и возбудимости клетки в разные фазы потенциала действия.
Д – фаза деполяризации, Рб – фаза быстрой реполяризации, Рм – фаза медленной реполяризации, Г – фаза гиперполяризации;
Н – период нормальной возбудимости, Ра – период абсолютной рефрактерности, Ро – период относительной рефрактерности, Н+ – период супернормальной возбудимости, Н- – период субнормальной возбудимости
14. что такое порог деполяризации?
Порог деполяризации-это разность межу МП (Ео) и крити-ческим уровнем деполяризации (Ек):
Порог деполяризации является мерой возбудимости. Чем меньше порог деполяризации, тем меньшей силы необходимо при-ложить раздражитель чтобы вызвать развитие потенциала дейс-твия
15. в чем заключаются механизмы реполяризации?
фаза, во время которой восстанавливается исходный по тенциал покоя мембраны нервной клетки после прохождения через нее нервного импульса. Во время прохождения нервного импульса происходит временное изменение молекулярной структуры мембраны, в результате которого ионы могут свободно проходить через нее. Во время реполяризации ионы диффундируют в обратном направлении для восстановления прежнего электрического заряда мембраны, после чего нерв бывает готов к дальнейшей передаче через него импульсов.
Почему величина потенциала действия равна +40?
Это связано с тем, что та короткое время, в течение которого были от-крыты натриевые каналы и проницаемость мембраны была увеличенной со-здается, равновесный диффузионный натриевый потенциал.
Почему восстанавливается исходный мембранный потенциал после окончания потенциала действия?
Этот процессе состоит из 3 составляющих:
-инактивации натриевых каналов;
-увеличения проницаемости потенциал-зависимых калиевых кана-лов;
-работы натрий/калиевого насоса по восстановлению ионных гради-ентов.
Видео:Гальванические элементы. 1 часть. 10 класс.Скачать
Уравнение нернста кратко и понятно
Равновесие между химическими и электрическими движущими силами определяет величину мембранного потенциала покоя. Состояние равновесия достигается, когда различие в свободной энергии этих сил равно нулю (другими словами, когда общий поток = 0):
Изменение свободной энергии, происходящее при движении через мембрану компонента X, можно выразить уравнением:
• R — газовая постоянная (2 кал моль-1 К-1)
• Т — абсолютная температура (К; 37 °С = 307,5 К)
• [Х]0 — концентрация X вне клетки
• [X]i — концентрация X внутри клетки
и изменение свободной энергии, обусловленное транспортом через мембрану заряда, связанного с растворенным компонентом X составляет:
• Em — равновесный потенциал (в вольтах)
• z — валентность иона (электрический заряд)
• F— число Фарадея (2,3 х 104 кал вольт-1 моль-1)
В состоянии равновесия
и после преобразования получаем.
Таким образом, значение равновесного потенциала или потенциала Нернста для одновалентного иона X при 37 °С определяется уравнением:
Если концентрация ионов известна, то уравнение Нернста можно использовать для расчета равновесного мембранного потенциала для каждого иона в отдельности. На рисунке ниже показаны результаты таких расчетов для плазматической мембраны мышечных клеток. Так, для [К+]0 = 4 мМ и [K+]i = 155 мМ значение мембранного потенциала Еm = -98 мВ, если учитывать только поток ионов К+, т. е. Еm = Еk.
Почти во всех покоящихся клетках млекопитающих плазматическая мембрана проницаема для ионов К+. Na+/К+-АТФаза поддерживает трансмембранный ионный градиент и создает внутри клетки относительно высокую концентрацию ионов К+ ([K+]i). При открытии некоторых К+-каналов ионы К+ начинают транспортироваться в направлении градиента концентрации, что приводит к появлению положительного заряда с внешней стороны мембраны и отрицательного с внутренней ее стороны. Этот отрицательный мембранный потенциал, Еm, представляет собой электродвижущую силу, которая препятствует дальнейшему выходу К+ из клетки в направлении градиента (химическая движущая сила). Таким образом, открытие в покоящейся клетке специальных селективных К+-каналов определяет значение отрицательного потенциала покоя, при котором не происходит транспорта К+ через мембрану и величина Еm остается постоянной.
Аналогично потенциал Нернста можно рассчитать и для других ионов. Если мембрана становится более проницаемой для определенных ионов, то мембранный потенциал Еm будет меняться, приближаясь к значению потенциала Нернста для этих ионов (обычно становясь более положительным при деполяризации мембраны).
Например, если плазматическая мембрана становится более проницаемой для ионов Na+, то они будут транспортироваться в направлении своего градиента концентрации. При этом мембрана будет приобретать отрицательный заряд с внешней стороны и положительный заряд с внутренней. В физиологических условиях, в покоящейся клетке, открытие нескольких Na+-каналов, наряду с постоянным притоком зарядов за счет протечки, приведет к поступлению Na+ в клетку, и значение мембранного потенциала покоя сдвинется в более положительную сторону (например, -82 мВ). Напротив, аналогичный расчет в случае ионов К+ показывает, что значение мембранного потенциала покоя составит -89 мВ. В клетках, обладающих меньшей проницаемостью для ионов К+ в результате фоновой утечки ионов Na+ и деполяризующих ионных потоков, величина мембранного потенциала покоя Em смещается в сторону более положительных значений (например, становится равной -50 мВ). При возбуждении клетки электрическим зарядом и открытии Na+ каналов, в состоянии теоретического равновесия между потоком Na+, направленным в клетку, и потоком К+, направленным в противоположную сторону, уровень мембранного потенциала оказывается ближе к ENa, а не к Ек. Согласно уравнению Нернста, равновесный потенциал для Na+ при 37 °С составляет:
Если [Na+]0 = 145 мМ и [Na+]i = 12 мМ (как для клеток мышц), то значение мембранного потенциала составляет Еm = +67 мВ, принимая во внимание транспорт только ионов Na+. Таким образом, суммарный эффект открытия Na+ каналов выражается в установлении потока ионов натрия, направленного в клетку, что приводит к сдвигу отрицательного потенциала покоя Еm до значения +67 мВ.
Аналогичным образом, когда плазматическая мембрана становится более проницаемой для Са2+, ионы транспортируются в направлении градиента концентрации. При этом мембрана на внешней стороне приобретает более отрицательный заряд, а на внутренней — более положительный. Когда под действием электрического заряда клетка возбуждается и открываются Са2+-каналы, теоретическое равновесие между потоком Са2+ в клетку и потоком К+ из клетки определяет уровень мембранного потенциала ближе к значению ЕCa. Согласно уравнению Нернста,
Если [Са2+]0 = 1,5 мМ и [Ca2+]i = 0,1 мкМ, как для мышечной клетки, то мембранный потенциал составляет Em = +129 мВ. Таким образом, суммарный эффект открытия Са2+ каналов выражается в установлении потока Са2+ в клетку, который приводит к сдвигу отрицательного потенциала покоя Еm, к +129 мВ. [Са2+-каналы открываются при более положительном значении потенциала действия, чем натриевые каналы. Это означает, что они открываются на более поздней фазе потенциала действия. Для ионов Cl_ по уравнению Нернста получаем
Если [Cl-]0 = 123 мМ и [Cl-]i= 4,2 мМ, то мембранный потенциал только для Cl- составляет Еm = -90 мВ. Таким образом, суммарный эффект открытия хлоридного канала приводит к выходу ионов Cl-, что стабилизирует отрицательное значение потенциала покоя Еm.
Концентрация свободных ионов и равновесные потенциалы клеток скелетных мышц млекопитающих.
Значения равновесных потенциалов рассчитаны для 37 °С, принимая величину потенциала покоя мембраны мышечной клетки равной -90 мВ.
Сверху обозначены относительные радиусы негидратированных ионов.
Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021
📽️ Видео
Уравнение Нернста. Условия изменения направления ОВР. Продукты в ОВР. Ч.5-3.Скачать
Уравнение Нернста #shortsbetaСкачать
ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Потенциал покоя и равновесный потенциалСкачать
Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать
Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать
ГИДРОЛИЗ СОЛЕЙ | 9 класс | Кратко и понятноСкачать
РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать
8 класс. ОВР. Окислительно-восстановительные реакции.Скачать
Химия | Молекулярные и ионные уравненияСкачать
Составление схемы и вычисление ЭДС гальванического концентрационного элемента | Уравнение НернстаСкачать
Проницаемость и мембранные потенциалыСкачать
МЕМБРАННЫЙ ПОТЕНЦИАЛ ПОКОЯ: формирование, роль калиевых каналов, равновесный потенциал || СТУДЕНТАМСкачать
ОВР часть 2. Окислительно-восстановительные реакции. Электродный потенциал.Скачать
