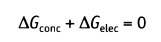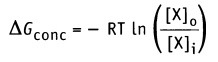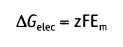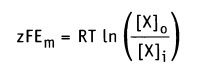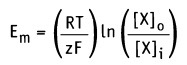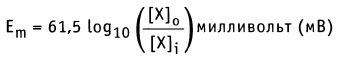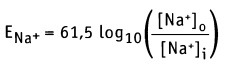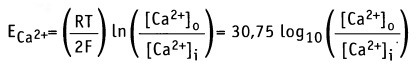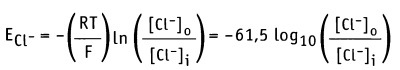Уравнение нернста и его применение (3 видео)

Уравнение нернста и его применение

Равновесие между химическими и электрическими движущими силами определяет величину мембранного потенциала покоя. Состояние равновесия достигается, когда различие в свободной энергии этих сил равно нулю (другими словами, когда общий поток = 0):

Изменение свободной энергии, происходящее при движении через мембрану компонента X, можно выразить уравнением:

• R — газовая постоянная (2 кал моль-1 К-1)
• Т — абсолютная температура (К; 37 °С = 307,5 К)
• [Х]0 — концентрация X вне клетки
• [X]i — концентрация X внутри клетки

и изменение свободной энергии, обусловленное транспортом через мембрану заряда, связанного с растворенным компонентом X составляет:

• Em — равновесный потенциал (в вольтах)
• z — валентность иона (электрический заряд)
• F— число Фарадея (2,3 х 104 кал вольт-1 моль-1)

В состоянии равновесия

и после преобразования получаем.

Таким образом, значение равновесного потенциала или потенциала Нернста для одновалентного иона X при 37 °С определяется уравнением:

Если концентрация ионов известна, то уравнение Нернста можно использовать для расчета равновесного мембранного потенциала для каждого иона в отдельности. На рисунке ниже показаны результаты таких расчетов для плазматической мембраны мышечных клеток. Так, для [К+]0 = 4 мМ и [K+]i = 155 мМ значение мембранного потенциала Еm = -98 мВ, если учитывать только поток ионов К+, т. е. Еm = Еk.

Почти во всех покоящихся клетках млекопитающих плазматическая мембрана проницаема для ионов К+. Na+/К+-АТФаза поддерживает трансмембранный ионный градиент и создает внутри клетки относительно высокую концентрацию ионов К+ ([K+]i). При открытии некоторых К+-каналов ионы К+ начинают транспортироваться в направлении градиента концентрации, что приводит к появлению положительного заряда с внешней стороны мембраны и отрицательного с внутренней ее стороны. Этот отрицательный мембранный потенциал, Еm, представляет собой электродвижущую силу, которая препятствует дальнейшему выходу К+ из клетки в направлении градиента (химическая движущая сила). Таким образом, открытие в покоящейся клетке специальных селективных К+-каналов определяет значение отрицательного потенциала покоя, при котором не происходит транспорта К+ через мембрану и величина Еm остается постоянной.

Аналогично потенциал Нернста можно рассчитать и для других ионов. Если мембрана становится более проницаемой для определенных ионов, то мембранный потенциал Еm будет меняться, приближаясь к значению потенциала Нернста для этих ионов (обычно становясь более положительным при деполяризации мембраны).

Например, если плазматическая мембрана становится более проницаемой для ионов Na+, то они будут транспортироваться в направлении своего градиента концентрации. При этом мембрана будет приобретать отрицательный заряд с внешней стороны и положительный заряд с внутренней. В физиологических условиях, в покоящейся клетке, открытие нескольких Na+-каналов, наряду с постоянным притоком зарядов за счет протечки, приведет к поступлению Na+ в клетку, и значение мембранного потенциала покоя сдвинется в более положительную сторону (например, -82 мВ). Напротив, аналогичный расчет в случае ионов К+ показывает, что значение мембранного потенциала покоя составит -89 мВ. В клетках, обладающих меньшей проницаемостью для ионов К+ в результате фоновой утечки ионов Na+ и деполяризующих ионных потоков, величина мембранного потенциала покоя Em смещается в сторону более положительных значений (например, становится равной -50 мВ). При возбуждении клетки электрическим зарядом и открытии Na+ каналов, в состоянии теоретического равновесия между потоком Na+, направленным в клетку, и потоком К+, направленным в противоположную сторону, уровень мембранного потенциала оказывается ближе к ENa, а не к Ек. Согласно уравнению Нернста, равновесный потенциал для Na+ при 37 °С составляет:

Если [Na+]0 = 145 мМ и [Na+]i = 12 мМ (как для клеток мышц), то значение мембранного потенциала составляет Еm = +67 мВ, принимая во внимание транспорт только ионов Na+. Таким образом, суммарный эффект открытия Na+ каналов выражается в установлении потока ионов натрия, направленного в клетку, что приводит к сдвигу отрицательного потенциала покоя Еm до значения +67 мВ.

Аналогичным образом, когда плазматическая мембрана становится более проницаемой для Са2+, ионы транспортируются в направлении градиента концентрации. При этом мембрана на внешней стороне приобретает более отрицательный заряд, а на внутренней — более положительный. Когда под действием электрического заряда клетка возбуждается и открываются Са2+-каналы, теоретическое равновесие между потоком Са2+ в клетку и потоком К+ из клетки определяет уровень мембранного потенциала ближе к значению ЕCa. Согласно уравнению Нернста,

Если [Са2+]0 = 1,5 мМ и [Ca2+]i = 0,1 мкМ, как для мышечной клетки, то мембранный потенциал составляет Em = +129 мВ. Таким образом, суммарный эффект открытия Са2+ каналов выражается в установлении потока Са2+ в клетку, который приводит к сдвигу отрицательного потенциала покоя Еm, к +129 мВ. [Са2+-каналы открываются при более положительном значении потенциала действия, чем натриевые каналы. Это означает, что они открываются на более поздней фазе потенциала действия. Для ионов Cl_ по уравнению Нернста получаем

Если [Cl-]0 = 123 мМ и [Cl-]i= 4,2 мМ, то мембранный потенциал только для Cl- составляет Еm = -90 мВ. Таким образом, суммарный эффект открытия хлоридного канала приводит к выходу ионов Cl-, что стабилизирует отрицательное значение потенциала покоя Еm.

Концентрация свободных ионов и равновесные потенциалы клеток скелетных мышц млекопитающих.
Значения равновесных потенциалов рассчитаны для 37 °С, принимая величину потенциала покоя мембраны мышечной клетки равной -90 мВ.
Сверху обозначены относительные радиусы негидратированных ионов.

Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021

Содержание

Применение уравнения Нернста в решении задач.
Пример 1:
Решение:
Пример 2:
Решение:
Уравнение Нернста.
💥 Видео

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

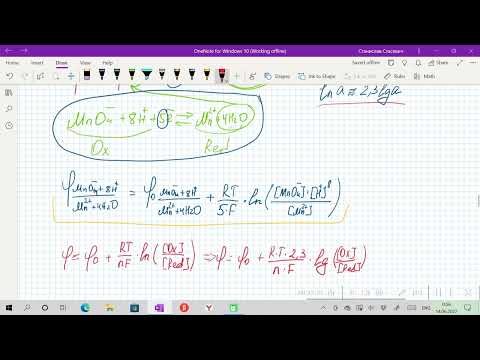
Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:

Получается, что потенциал KMnO₄ стал меньше, чем у хлора, а значит, реакция не пойдет.

Видео:Уравнение НернстаСкачать

Уравнение Нернста.

Уравнение было получено немецким физико-химиком В. Нернстом. Оно связывает электродный потенциал с природой металла, концентрацией его ионов в растворе и абсолютной температурой. Вывод уравнения основан на применении второго начала термодинамики к процессу (6). Для вывода уравнения рассмотрим металл, который представляет собой металлическую пластинку, опущенную в раствор своей соли. Такая система носит название металлический электрод.

Электрическая работа по переносу 1 моль катионов с поверхности металла в раствор или обратно равна произведению суммарного перенесенного заряда Z∙F на разность потенциалов φ_M Z + _/_M

где Z – зарядовое число катиона или число электронов, принимающих участие в процессе; F- постоянная Фарадея, равная 96500 Кл/моль; φ_M Z + _/_M – электродный потенциал, В.

Согласно второму закону термодинамики, максимальная работа, совершаемая закрытой системой в изобарно-изотермическом процессе (то есть при Р, Т = const), равна убыли её энергии Гиббса

Можно получить, используя уравнение изотермы химической реакции, что изменение энергии Гиббса в ходе процесса (6) равно

где a_M – относительная (отнесенная к стандартной) активность металла в кристалле;

a_M Z + — относительная активность ионов металла в растворе.

Из выражений (9) и (10) получаем

Приравнивая выражения для электрической работы (8) и (11), получаем после несложных преобразований уравнение Нернста для металлического электрода

Так как К 0 – стандартная термодинамическая константа равновесия реакции, то при Т = const она является постоянной величиной. Поэтому для данного электрода первое слагаемое в выражении (12) является постоянной величиной. Его обозначают через

φ 0 _М/_M Z + и называют стандартным электродным потенциалом.

Активность металла а_М в его кристалле для индивидуального вещества является стандартной активностью и равна 1, то есть

Тогда получаем выражение для уравнения Нернста, используемое в практических расчетах

В разбавленных растворах электролитов коэффициенты активности ионов равны их концентрациям. Поэтому уравнение Нернста можно представить в следующем виде, если иcпользовать молярные концентрации ионов С_М Z +

Таким образом, потенциал металлического электрода зависит от природы металла и от условий, в которых находится раствор. Зависимость электродного потенциала от природы характеризуется величиной φ 0 _M Z + _/_M , которая представляет собой табличное значение стандартного потенциала. Данное значение обычно берут из справочников. Зависимость от температуры раствора и концентрации ионов в растворе определяется вторым слагаемым уравнения Нернста. Как видно из (15), потенциал металлического электрода увеличивается с ростом температуры и концентрации ионов металла в растворе.

Отметим, что иногда встречается выражение уравнения Нернста, имеющего вид

Данное уравнение получается при условии Т = 298 К; R = 8,31 Дж/(моль∙К); F = 96500 Кл/моль и замене натурального логарифма на десятичный.

В наиболее общем случае уравнение Нернста записывается для электродного процесса

Ox + Ze — ↔ Red (17),

где Ox – окисленная форма частиц, участвующих в реакции; Red – восстановленная форма частиц, участвующих в реакции. Уравнение Нернста для этого процесса записывается следующим образом

φ_Ox/Red = φ 0 _Ox/Red + ln (a_Ox/a_Red) (18).

Зависимость электродного потенциала от природы окислительно-восстановительной системы характеризуется величиной φ 0 _Ox_/_Red, которую обычно находят из справочных таблиц, зависимость от температуры и активностей окисленной и восстановленной форм определяется вторым слагаемым из (18).

Потенциал окислительно-восстановительной системы увеличивается с ростом температуры и активности окисленной формы и уменьшается с ростом активности восстановленной формы.

Дата добавления: 2015-08-08 ; просмотров: 3344 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ