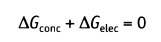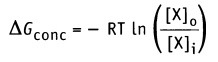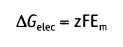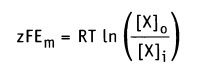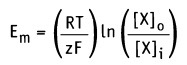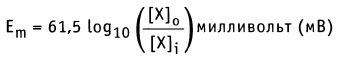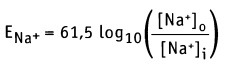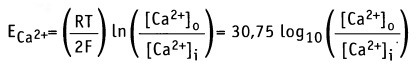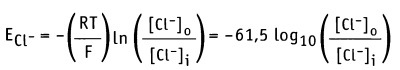Уравнение нернста и его анализ (6 видео)

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Содержание

Пример 1:
Решение:
Пример 2:
Решение:
Уравнение нернста и его анализ
Уравнение Нернста. Потенциометрические методы анализа
🎬 Видео

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:

Получается, что потенциал KMnO₄ стал меньше, чем у хлора, а значит, реакция не пойдет.

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Уравнение нернста и его анализ

Равновесие между химическими и электрическими движущими силами определяет величину мембранного потенциала покоя. Состояние равновесия достигается, когда различие в свободной энергии этих сил равно нулю (другими словами, когда общий поток = 0):

Изменение свободной энергии, происходящее при движении через мембрану компонента X, можно выразить уравнением:

• R — газовая постоянная (2 кал моль-1 К-1)
• Т — абсолютная температура (К; 37 °С = 307,5 К)
• [Х]0 — концентрация X вне клетки
• [X]i — концентрация X внутри клетки

и изменение свободной энергии, обусловленное транспортом через мембрану заряда, связанного с растворенным компонентом X составляет:

• Em — равновесный потенциал (в вольтах)
• z — валентность иона (электрический заряд)
• F— число Фарадея (2,3 х 104 кал вольт-1 моль-1)

В состоянии равновесия

и после преобразования получаем.

Таким образом, значение равновесного потенциала или потенциала Нернста для одновалентного иона X при 37 °С определяется уравнением:

Если концентрация ионов известна, то уравнение Нернста можно использовать для расчета равновесного мембранного потенциала для каждого иона в отдельности. На рисунке ниже показаны результаты таких расчетов для плазматической мембраны мышечных клеток. Так, для [К+]0 = 4 мМ и [K+]i = 155 мМ значение мембранного потенциала Еm = -98 мВ, если учитывать только поток ионов К+, т. е. Еm = Еk.

Почти во всех покоящихся клетках млекопитающих плазматическая мембрана проницаема для ионов К+. Na+/К+-АТФаза поддерживает трансмембранный ионный градиент и создает внутри клетки относительно высокую концентрацию ионов К+ ([K+]i). При открытии некоторых К+-каналов ионы К+ начинают транспортироваться в направлении градиента концентрации, что приводит к появлению положительного заряда с внешней стороны мембраны и отрицательного с внутренней ее стороны. Этот отрицательный мембранный потенциал, Еm, представляет собой электродвижущую силу, которая препятствует дальнейшему выходу К+ из клетки в направлении градиента (химическая движущая сила). Таким образом, открытие в покоящейся клетке специальных селективных К+-каналов определяет значение отрицательного потенциала покоя, при котором не происходит транспорта К+ через мембрану и величина Еm остается постоянной.

Аналогично потенциал Нернста можно рассчитать и для других ионов. Если мембрана становится более проницаемой для определенных ионов, то мембранный потенциал Еm будет меняться, приближаясь к значению потенциала Нернста для этих ионов (обычно становясь более положительным при деполяризации мембраны).

Например, если плазматическая мембрана становится более проницаемой для ионов Na+, то они будут транспортироваться в направлении своего градиента концентрации. При этом мембрана будет приобретать отрицательный заряд с внешней стороны и положительный заряд с внутренней. В физиологических условиях, в покоящейся клетке, открытие нескольких Na+-каналов, наряду с постоянным притоком зарядов за счет протечки, приведет к поступлению Na+ в клетку, и значение мембранного потенциала покоя сдвинется в более положительную сторону (например, -82 мВ). Напротив, аналогичный расчет в случае ионов К+ показывает, что значение мембранного потенциала покоя составит -89 мВ. В клетках, обладающих меньшей проницаемостью для ионов К+ в результате фоновой утечки ионов Na+ и деполяризующих ионных потоков, величина мембранного потенциала покоя Em смещается в сторону более положительных значений (например, становится равной -50 мВ). При возбуждении клетки электрическим зарядом и открытии Na+ каналов, в состоянии теоретического равновесия между потоком Na+, направленным в клетку, и потоком К+, направленным в противоположную сторону, уровень мембранного потенциала оказывается ближе к ENa, а не к Ек. Согласно уравнению Нернста, равновесный потенциал для Na+ при 37 °С составляет:

Если [Na+]0 = 145 мМ и [Na+]i = 12 мМ (как для клеток мышц), то значение мембранного потенциала составляет Еm = +67 мВ, принимая во внимание транспорт только ионов Na+. Таким образом, суммарный эффект открытия Na+ каналов выражается в установлении потока ионов натрия, направленного в клетку, что приводит к сдвигу отрицательного потенциала покоя Еm до значения +67 мВ.

Аналогичным образом, когда плазматическая мембрана становится более проницаемой для Са2+, ионы транспортируются в направлении градиента концентрации. При этом мембрана на внешней стороне приобретает более отрицательный заряд, а на внутренней — более положительный. Когда под действием электрического заряда клетка возбуждается и открываются Са2+-каналы, теоретическое равновесие между потоком Са2+ в клетку и потоком К+ из клетки определяет уровень мембранного потенциала ближе к значению ЕCa. Согласно уравнению Нернста,

Если [Са2+]0 = 1,5 мМ и [Ca2+]i = 0,1 мкМ, как для мышечной клетки, то мембранный потенциал составляет Em = +129 мВ. Таким образом, суммарный эффект открытия Са2+ каналов выражается в установлении потока Са2+ в клетку, который приводит к сдвигу отрицательного потенциала покоя Еm, к +129 мВ. [Са2+-каналы открываются при более положительном значении потенциала действия, чем натриевые каналы. Это означает, что они открываются на более поздней фазе потенциала действия. Для ионов Cl_ по уравнению Нернста получаем

Если [Cl-]0 = 123 мМ и [Cl-]i= 4,2 мМ, то мембранный потенциал только для Cl- составляет Еm = -90 мВ. Таким образом, суммарный эффект открытия хлоридного канала приводит к выходу ионов Cl-, что стабилизирует отрицательное значение потенциала покоя Еm.

Концентрация свободных ионов и равновесные потенциалы клеток скелетных мышц млекопитающих.
Значения равновесных потенциалов рассчитаны для 37 °С, принимая величину потенциала покоя мембраны мышечной клетки равной -90 мВ.
Сверху обозначены относительные радиусы негидратированных ионов.

Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021

Видео:Уравнение НернстаСкачать

Уравнение Нернста. Потенциометрические методы анализа

Потенциометрические методы основаны на измерении электродвижущих сил (ЭДС):

где E — электродвижущая сила (ЭДС);
E₁ и E₂ — потенциалы электродов исследуемой цепи.

Потенциал электрода E связан с активностью и концентрацией веществ, участвующих в электродном процессе, уравнением Нернста:

где E0 — стандартный потенциал редокс-системы;
R — универсальная газовая постоянная, равная 8,312 Дж/(моль К);
T — абсолютная температура, К;
F — постоянная Фарадея, равная 96485 Кл/моль;
n — число электронов, принимающих участие в электродной реакции;
a_ox, a_red — активности соответственно окисленной и восстановленной форм редокс-системы;
[ox], [red] — их молярные концентрации;
Г_ox, Г_red — коэффициенты активности.

E=E₀ при a_ox = a_red = 1, причем имеется в виду гипотетический стандартный 1 М раствор, в котором коэффициент активности каждого растворенного вещества равен 1, а чистые вещества находятся в наиболее устойчивом физическом состоянии при данной температуре и нормальном атмосферном давлении.

Подставляя T=298,15 и числовые значения констант в уравнение, получаем для 25 °C

Однако потенциал отдельного электрода экспериментально определить невозможно. Относительные значения электродного потенциала находят, комбинируя данный электрод со стандартным водородным электродом, который является общепринятым международным стандартом. Потенциал водородного электрода принят равным нулю при всех температурах, поэтому потенциал данного электрода — это, в сущности, ЭДС элемента, состоящего из данного и стандартного водородного электрода.

Конструктивно стандартный водородный электрод представляет собой платинированную платиновую пластинку, омываемую газообразным водородом при давлении 1,013 . 10 5 Па (1 атм) и погруженную в раствор кислоты с активностью ионов H + , равной единице. При работе водородного электрода протекает реакция

В практической работе вместо хрупкого и нередко капризного водородного электрода применяют специальные, более удобные в работе стабильные электроды сравнения, потенциал которых по отношению к стандартному водородному электроду точно известен.

Уравнение (2) можно переписать

Величину E₀‘ называют формальным потенциалом. Как видно, формальный потенциал характеризует систему, в которой концентрации (а не активности) всех участников равны 1,0 моль/л. Формальный потенциал включает в себя коэффициенты активности, т.е. зависит от ионной силы раствора. Если коэффициент активности равен 1, то E₀‘=E₀, т.е. формальный потенциал совпадает со стандартным. Точность такого приближения для многих расчетов оказывается достаточной.

Природа возникновения потенциала различна. Можно выделить следующие три основные классы потенциалов, которые не исчерпывают, конечно, всего многообразия. Это:

Электродные потенциалы.
Редокс-потенциалы.
Мембранные потенциалы.

Хотя по термином «электродный потенциал» нередко имеют в виду любой потенциал, независимо от механизма его возникновения, в более узком понимании — это потенциал непосредственно связанный с материалом электрода. Например, цинковый электрод:

Активность свободного металла принимается равной единице. Электродные потенциалы отличаются от редокс-потенциалов, для которых материал электрода не имеет значения, так как они химически инертны по отношению ко всем веществам в растворе, и от мембранных, для которых разность потенциалов на мембране измеряется с помощью пары других (в принципе, возможно, одинаковых) электродов.

Потенциометрические методы анализа известны с конца прошлого века, когда Нернст вывел (1889) известное уравнение (1), а Беренд сообщил (1883) о первом потенциометрическом титровании. Интенсивное развитие потенциометрии в последние годы связано, главным образом, с появлением разнообразных типов ионоселективных электродов, позволяющих проводить прямые определения концентрации многих ионов в растворе, и успехами в конструировании и массовом выпуске приборов для потенциометрических измерений.

Потенциометрические методы анализа подразделяют на прямую потенциометрию (ионометрию) и потенциометрическое титрование. Методы прямой потенциометрии основаны на прямом применении уравнения Нернста (1) для нахождения активности или концентрации участника электродной реакции по экспериментально измеренной ЭДС цепи или потенциалу соответствующего электрода. При потенциометрическом титровании точку эквивалентности определяют по резкому изменению (скачку) потенциала вблизи точки эквивалентности.

Васильев В. П. Аналитическая химия. В 2 кн. Кн. 2. Физико-химические методы анализа: Учеб. для студ. вузов, обучающихся по химико-технол. спец. — 2-е изд., перераб. и доп. — М.:Дрофа, 2002. — 384 с., ил. — С. 179-181.