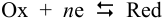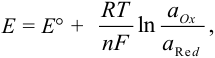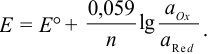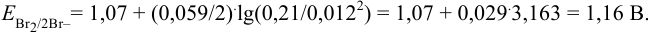Уравнение нернста для стандартных расчетов (2 видео)

Содержание

Вычисление потенциала в реальных условиях. Уравнение Нернста с примером решения
Вычисление потенциала в реальных условиях. Уравнение Нернста
Пример 5.4 .
Применение уравнения Нернста в решении задач.
Пример 1:
Решение:
Пример 2:
Решение:
Решение задач с использованием уравнения Нернста (Nernst)
Решение задач по химии с использованием уравнениея Нернста
📸 Видео

Видео:Гальванические элементы. 1 часть. 10 класс.Скачать

Вычисление потенциала в реальных условиях. Уравнение Нернста с примером решения

Вычисление потенциала в реальных условиях. Уравнение Нернста

В реальных условиях химического равновесия величина потенциала зависит от температуры и активностей окисленной и восстановленной форм. Количественно эта зависимость равновесного потенциала пары (Е) выражается уравнением Нернста:

для полуреакции

уравнение Нернста

где: R — универсальная газовая постоянная ();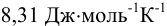

F — число Фарадея ();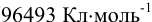

Т- абсолютная температура (К);

Е — равновесный потенциал.

После подстановки постоянных величин и переходя к десятичным логарифмам, получаем коэффициенты 0,059 при 25°С и 0,058 при 20°С.

Тогда уравнение Нернста при 25°С можно записать так:

Обычно вместо активностей в расчетах используют концентрации окисленной и восстановленной форм, пренебрегая различием в величинах коэффициентов активностей обеих форм, которые при близких значениях сокращаются в уравнении (5.3).

Пример 5.4 .

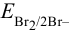
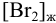
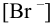
Вычислить , если = 0,21 моль/л, а = 0,012 моль/л.

Решение:

Записываем уравнение полуреакции:

Записываем уравнение Нернста для данной полуреакции:

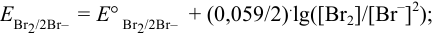
Эти примеры взяты со страницы примеров решения задач по аналитической химии:

Возможны вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:

Получается, что потенциал KMnO₄ стал меньше, чем у хлора, а значит, реакция не пойдет.

Видео:Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать

Решение задач с использованием уравнения Нернста (Nernst)

Видео:011 Электрохимия 4 уравнение НернстаСкачать

Решение задач по химии с использованием уравнениея Нернста

Задание 246.
Потенциал серебряного электрода в растворе АgNO₃ составил 95% от значения его стандартного электронного потенциала. Чему равна концентрация ионов Аg+ (моль/л). Ответ: 0,20 моль/л.
Решение:
Электродный потенциал металла (Е)зависит от концентрации его ионов в растворе. Эта зависимость выражается уравнением Нернста:

Е 0 – стандартный электродный потенциал металла; n – число электронов, принимающих участие в процессе; с – концентрация ионов металла в растворе его соли (при точных вычислениях – активность). Используя уравнение Нернста, получим выражение для расчета концентрации ионов Ag + в растворе:

Ответ: 0,20 моль/л.

Задание 247.
Составьте схему, напишите электронные уравнения электродных процессов, и вычислите ЭДС медно-кадмиевого гальванического элемента, в котором [Сd 2+ ] = 0,8 моль/л, а [Сu 2+ ] = 0,01 моль/л. Ответ: 0,68 В.
Решение:
Схема данного гальванического элемента:

Вертикальная линейка обозначает поверхность раздела между металлом и раствором, а две линейки — границу раздела двух жидких фаз — пористую перегородку (или соединительную трубку, заполненную раствором электролита). Кадмий имеет меньший потенциал (—0,403 В) и является анодом, на котором протекает окислительный процесс:

Cd 0 — 2 = Cd 2+ (1)

Медь, потенциал которой +0,34 В, катод, т.е. электрод, на котором протекает восстановительный процесс:

Cu 2+ + 2 = Cu 0 (2)

Уравнение окислительно-восстановительной реакции, характеризующее работу данного гальванического элемента, можно получить, сложив электронные уравнения анодного (1) и катодного (2) процессов:

Cd 0 + Cu 2+ = Cd 2+ + Cu 0

Электродный потенциал металла (Е) зависит от концентрации его ионов в растворе. Эта зависимость выражается уравнением Нернста:

Е 0 – стандартный электродный потенциал металла; n – число электронов, принимающих участие в процессе; с – концентрация ионов металла в растворе его соли (при точных вычислениях – активность). Определим электродные потенциалы кадмия и меди при заданных концентрациях:

Для определения ЭДС гальванического элемента из потенциала катода следует вычесть потенциал анода. Так как концентрация ионов в растворе 1 молы/л, то ЭДС элемента равна разности стандартных потенциалов двух его электродов:

Ответ: 0,68 В.

Задание 248.
Составьте схемы двух гальванических элементов, в одном из которых медь была бы катодом, а в другом — анодом. Напишите для каждого из этих элементов электронные уравнения реакций, протекающих на катоде и на аноде.
Решение:
а) Схема гальванического элемента, в котором медь является катодом:

Вертикальная линейка обозначает поверхность раздела между металлом и раствором, а две линейки — границу раздела двух жидких фаз — пористую перегородку (или соединительную трубку, заполненную раствором электролита). Цинк имеет меньший потенциал (-0,763 В) и является анодом, на котором протекает окислительный процесс:

Zn 0 — 2 = Zn 2+ (1)

Медь, потенциал которой +0,34 В, катод, т.е. электрод, на котором протекает восстановительный процесс:

Cu 2+ + 2 = Сu 0 (2)

Zn 0 + Cu 2+ = Zn 2+ + Cu 0

б) Схема гальванического элемента, в котором медь является анодом:

Медь имеет меньший потенциал (+0,34 В) и является анодом, на котором протекает окислительный процесс:

Cu 0 — 2 = Cu 2+ (1)

Платина, потенциал которой +1,19 В, катод, т.е. электрод, на котором протекает восстановительный процесс:

Pt 2+ + 2 = Pt 0 (2)

Сu 0 + Pt 2+ = Cu 2+ + Pt 0

Задание 249.
При какой концентрации ионов Сu 2+ (моль/л) значение потенциала медного электрода становится равным стандартному потенциалу водородного электрода? Ответ: 2,98 . 10 -12 моль/л..
Решение:
Определим концентрацию ионов Cu 2+ , при которой потенциал медного электрода равен 0,00 В, получим:

Ответ: 2,98 . 10 -12 моль/л.

Задание 250.
Какой гальванический элемент называют концентрационным? Составьте схему, напишите электронные уравнения электродных процессов и вычислите ЭДС гальванического элемента, состоящего из серебряных электродов, опущенных: первый в 0,01 н., а второй в 0,1 н. растворы AgNO₃. Ответ: 0,059 В.
Решение:
Гальванический элемент, работа которого основана на различных концентрациях ионов металла у катода и у анода, называется концентрационным. Обычно катод и анод сделаны из одного и того же металла, опущенных в растворы своей соли разной концентрации. Электродный потенциал металла (Е) зависит от концентрации его ионов в растворе. Эта зависимость выражается уравнением Нернста:

Е 0 – стандартный электродный потенциал металла; n – число электронов, принимающих участие в процессе; с – концентрация ионов металла в растворе его соли (при точных вычислениях – активность). Определим электродные потенциалы серебряных электродов при разных концентрациях ионов серебра Ag+, получим: