Уравнение нернста для равновесной электрохимической цепи (3 видео)

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Содержание

Пример 1:
Решение:
Пример 2:
Решение:
Стандартный водородный электрод
Характер потенциального скачка на границе раздела. Концепция электродного потенциала
Потенциальный скачок на границе раздела электрод — раствор
Стандартный водородный электрод. стандартные электродные потенциалы
Уравнение Нернста. ЭДС равновесной электрохимической цепи, ее связь с изменением энергии Гиббса электрохимической реакции
Вывод:
📽️ Видео

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

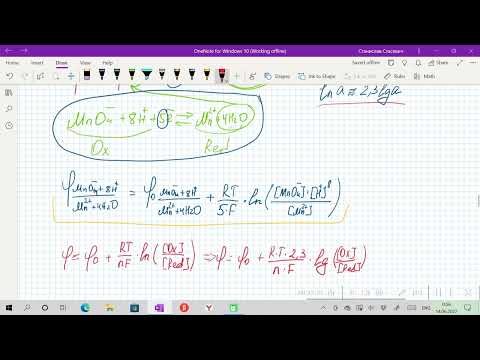
Получается, что потенциал KMnO₄ стал меньше, чем у хлора, а значит, реакция не пойдет.

Стандартный водородный электрод

Содержание:

Предмет:	Химия
Тип работы:	Курсовая работа
Язык:	Русский
Дата добавления:	21.04.2019

Данный тип работы не является научным трудом, не является готовой выпускной квалификационной работой!
Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала для самостоятельной подготовки учебной работы.

Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!

По этой ссылке вы сможете найти много готовых курсовых работ по химии:

Посмотрите похожие темы возможно они вам могут быть полезны:

Введение:

Причиной скачков потенциала является переход заряженных частиц (электронов, ионов) из одной фазы в другую.

Диффузионный потенциал — возникает на границе раздела растворов электролитов, которые различаются по природе или концентрации.

В элементе Якоби-Даниэля ионы переносятся во внутренней цепи от правой половины элемента к левой (это цепь переноса). Контакт растворов осуществляется через пористую диафрагму или солевой мостик с использованием растворов электролитов KCI, KNO3, NH4Cl, NH4NO3, ионы которых имеют примерно одинаковую подвижность (KCl = 73,5; = 76,35 Ом-1 см2 экв-1) уменьшить.

не всегда можно рассчитать, поэтому они часто пытаются его уменьшить. Для цепи (-) Pt, CI2 | Раствор HCI | CI2, Pt (+).

отсутствует (цепь без переноса), так как оба электрода помещены в один и тот же раствор соляной кислоты.

Характер потенциального скачка на границе раздела. Концепция электродного потенциала

Потенциал контакта возникает, когда два металлических электрода находятся в контакте или когда два металла связаны друг с другом через другие металлы. Разность контактных потенциалов определяется только природой крайних металлов. Если гальванический элемент имеет два одинаковых электрода в начале и в конце цепи = 0 (поскольку цепь правильно разомкнута).

Когда заряженные частицы переходят из одной фазы в другую, в дополнение к химической работе, также выполняется электрическая работа, и электрохимическое состояние заряженной частицы в фазе называется электрохимическим потенциалом (химический потенциал + электрическая энергия частицы).

В окислительно-восстановительной среде значение стандартного электродного потенциала через значения его химических окислительно-восстановительных потенциалов в стандартных условиях будет иметь вид.

Абсолютный электродный потенциал? потенциальный скачок между металлом и раствором.

Потенциальный скачок на границе раздела электрод — раствор

Когда проводник типа I (металлический) вступает в контакт с раствором электролита (проводник типа II), на границе раздела металл-раствор появляется двойной электрический слой (DES).

Видео:Уравнение НернстаСкачать

Во-первых, представьте, что цинковый электрод помещен в воду. Известно, что в кристаллической решетке металлов есть катионы и атомы, которые занимают определенные места в узлах решетки, и относительно свободные электроны движутся между катионами. Под воздействием полярных молекул воды катионы цинка отрываются от цинковой пластины и переходят в слой воды, прилегающий к поверхности металла. В этом случае электрод заряжается отрицательно, а раствор заряжается положительно благодаря катионам, которые в него попали. Между металлом и раствором образуется двойной электрический слой, и происходит скачок потенциала.

Появление электрического заряда на электроде предотвращает дальнейший переход катионов в раствор. При достижении определенной концентрации ионов в растворе устанавливается динамическое равновесие, которое сопровождается непрерывным обменом катионов между металлом и раствором.

Между металлом и раствором устанавливается скачок равновесного потенциала.

Подобные взаимодействия происходят, когда металл погружается в солевой раствор этого металла. Однако равновесие возникает при другом значении скачка потенциала, определяемом концентрацией ионов металлов в растворе.

В результате этих процессов раствор вблизи металла приобретает заряд, противоположный по знаку заряду металла, так как большинство катионов расположены на отрицательно заряженной поверхности металла, образуя плотный слой толщиной d. Двойной электрический слой DES сформирован. Этот слой характеризуется различным распределением ионов разных знаков в поверхностном слое раствора и неравномерным распределением зарядов в поверхностном слое металла. Это связано с определенной разностью потенциалов (скачок потенциала) на границе раздела металл / раствор. Некоторые из катионов металлов перемещаются из металла в глубину раствора и образуют диффузную часть ДЭС толщиной. Толщина этого слоя в растворе зависит от концентрации раствора, заряда металла и температуры.

Для металлов с низкой активностью, например меди, серебра и т. д., металл заряжен положительно, а соседний раствор заряжен отрицательно.

Очевидно, что если металл положительно заряжен при погружении в раствор, концентрация катионов в диффузном слое будет уменьшена, а концентрация анионов увеличена по сравнению с их концентрацией в растворе.

Таким образом, когда металл погружается в воду или раствор, содержащий ионы данного металла, на границе раздела металл / раствор образуется двойной электрический слой, и между металлом и раствором возникает разность потенциалов (скачок потенциала). Величина этой разности потенциалов зависит от свойств металла и раствора, в частности от концентрации ионов данного металла в растворе и от характера взаимодействия между частицами в двойном электрическом слое.

ДЭС по данным русского ученого Р.А. Колли похож на плоский конденсатор, одна пластинка которого находится на поверхности металла, другая находится в растворе на расстоянии диаметра молекулы воды.

Первые представления о структуре двойного электрического слоя были предложены русским ученым Р.А. Колли (1878), затем Л. Гельмгольц (1879), Т. Гай (1910) и Д. Чепмен (1913). Основы современной теории двойного электрического слоя были разработаны О. Штерном (1924), разработанным академиком А.Н. Фрумкин с сотрудниками.

Стационарный равновесный потенциал характеризуется непрерывным обменом заряженными частицами между электродом и раствором (это обменный ток, открытый В. Батлером (1936), его наличие было подтверждено методом меченых частиц).

Рассматриваемые металлические элементы являются обратимыми по отношению к катионам, т.е. обмениваются катионами с раствором — это ионы, определяющие потенциал (POI), поскольку скачок потенциала зависит от их концентрации.

В этом случае двойной электрический слой образуется в результате обмена анионами, которые определяют потенциал.

Стандартный водородный электрод. стандартные электродные потенциалы

Как упомянуто выше, абсолютное значение скачка потенциала на границе раздела электрод-раствор не может быть измерено экспериментально. Для практического определения потенциала электрода действуйте следующим образом: экспериментально измерьте ЭДС гальванического элемента, состоящего из двух электродов, и потенциал одного из них обычно принимается равным нулю.

Международным стандартом для сравнения электродных потенциалов является стандартный водородный электрод. Это платиновая пластина, покрытая платиновой сажей и насыщенная водородом H2 при p = 1 атм. Пластина погружается в раствор, где активность ионов водорода = 1 моль / дм3. Платина катализирует электродный процесс 2H + + 2e — H2. Электрохимическая схема стандартного водородного электрода: Pt, H2 (p = 1 атм) | H2SO4 (= 1 моль / дм3).

В этих условиях потенциал электрода водородного электрода принимается равным нулю = 0 и не зависит от температуры.

Видео:Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать

На основании решений Международной конвенции (Стокгольм, 1953 г.) для определения потенциала электрода создается гальваническая цепь, состоящая из измеряемого электрода и стандартного водородного электрода. При записи электрохимических цепей электрод с меньшим значением потенциала электрода (анод) записывается слева, а электрод с большим значением (катод) справа.

Например:

(-) Zn | ZnSO4 || CuSO4 | Cu (+)
(-) Zn — 2e> Zn2 + — процесс окисления
(+) Cu2 + + 2e> Cu — процесс восстановления
Zn + Cu2 +> Zn2 ++ Cu — общая токообразующая реакция.

Схема электрохимического контура с водородным электродом правильно написана в следующей последовательности: слева — стандартный водородный электрод, затем POI или весь электролит, а затем электрод: Pt, H2 (p = 1) | H2SO4 (= 1) || ZnSO4 | Zn.

В гальваническом элементе электроны перейдут от цинка к водородному электроду Pt, H2 (p = 1) | H2SO4 (= 1) || ZnSO4 | Zn.

Здесь будет происходить та же реакция, как если бы цинк был погружен в раствор серной кислоты (H2SO4). Электроны перешли бы от цинка к кислоте.

Для неактивных металлов, таких как медь, поток электронов идет от водородного электрода к медному электроду.

Измерьте ЭДС гальванического элемента в условиях равновесия.

Считается, что если поток электронов идет справа налево, то ЭДС отрицательна; если поток электронов идет слева направо, то ЭДС положительна.

В первом случае с цинком значение ЭДС отрицательно, во втором случае с медью значение ЭДС положительно, когда поток электронов идет слева направо.

Поскольку значение потенциала стандартного водородного электрода принимается равным нулю (= 0), ЭДС цепи равна потенциалу электрода измеряемого электрода.

При условии, что активность определяющих потенциал ионов составляет aPOI = 1 моль / дм3, потенциалы электродов называются стандартными, значения приведены в таблице при 25 ° C, они зависят от химической природы электрода, от заряда его ионы в растворе и выражаются в вольтах (V).

Расположенные в порядке возрастания стандартных электродных потенциалов, металлы представляют собой известную серию металлических напряжений.

Если aPOI ≥ 1, то потенциал электрода μ не является стандартным, и его зависимость от концентрации ионов определяется уравнением Нернста.

Уравнение Нернста. ЭДС равновесной электрохимической цепи, ее связь с изменением энергии Гиббса электрохимической реакции

Химическая энергия реакции в гальваническом элементе является источником электрической энергии. Наиболее важной количественной характеристикой гальванического элемента является ЭДС, которая равна разности потенциалов электрода: потенциал левого электрода (анода) вычитается из потенциала правого электрода, который больше по величине (катода).

Например, если в ячейке Якоби-Даниэля электрохимическая реакция Zn + Cu2 + = Zn2 + + Cu осуществляется в обратимых (равновесных) условиях, то выполняемая ею работа максимально равна работе электрических сил.

Видео:Лекция 4 Уравнение Нернста. Электрохимическое равновесиеСкачать

Если все процессы обратимы при постоянной температуре и давлении, то электрические работы, выполняемые гальваническим элементом, равны произведению ЭДС и количеству переданного электричества.

Максимальная работа реакции определяется уменьшением изобарико-изотермического потенциала согласно уравнению изотермы для элемента Якоби-Даниэля.

Это основное уравнение ЭДС гальванического элемента, состоящего из двух металлических электродов; его часто называют уравнением Нернста для определения ЭДС гальванического элемента.

Если активность ионов металлов в растворе не равна единице, то электродный потенциал металла не является стандартным. Зависимость потенциала металлического электрода от активности определяющих потенциал ионов в растворе определяется уравнением потенциала электрода Нернста.

Вывод этой формулы может быть дан на основе основного уравнения ЭДС гальванического элемента. Для определения потенциала электрода, как упомянуто выше, изготавливают гальванический элемент, один из полуэлементов которого является стандартным водородным электродом, а другой — испытательным, например медным.

Электрод представляет собой систему, в простейшем случае состоящую из двух фаз, из которых твердое тело имеет электронную, а другая — жидкость имеет ионную проводимость. Твердая фаза с электронной проводимостью считается проводником типа I, а жидкая фаза с ионной проводимостью считается II типом. Когда эти два проводника вступают в контакт, образуется двойной электрический слой (DES). Это может быть результатом ионного обмена между твердой и жидкой фазами или результатом специфической адсорбции катионов или анионов на поверхности твердой фазы, когда она погружена в воду или раствор.

С ионным механизмом образования DEL, например, в случае, когда химический потенциал атомов на поверхности металла (твердой фазы) больше, чем химический потенциал ионов в растворе, тогда атомы с поверхности металла перейдут в раствор в виде катионов: Me  Mez + + ze-. Высвобожденные электроны заряжают поверхность твердой фазы отрицательно и, как следствие, притягивают положительно заряженные ионы раствора к поверхности. В результате на поверхности раздела образуются два противоположно заряженных слоя, которые являются пластинами своего рода конденсатора. Для дальнейшего перехода заряженных частиц из одной фазы в другую им необходимо выполнить работу, равную разности потенциалов пластин этого конденсатора. Если химический потенциал атомов на поверхности твердой фазы меньше, чем химический потенциал ионов в растворе, то катионы из раствора переходят на поверхность твердой фазы, заряжая его положительно: Mez ++ ze-Me , Как в первом, так и во втором случае эти процессы не протекают бесконечно, но до установления динамического равновесия, которое может быть представлено обратимым окислительно-восстановительным переходом типа Me —  Mez + или, в общем случае, Ox + Редз +.

Процессы, в которых возврат или присоединение электронов происходит на электродах, называются электродом.

К сожалению, невозможно экспериментально установить внутренние потенциалы отдельных фаз  (Me) и  (p — p). Любая попытка подключить раствор с помощью провода к измерительному устройству вызывает появление новой поверхности контакта раствора металла, то есть появление нового электрода с собственной разностью потенциалов, которая влияет на измеряемый.

Однако можно измерить разницу  (Me) —  (p — p) гальванической ячейкой. Гальваническая ячейка — это система, состоящая из двух разных электродов, которая способна самопроизвольно преобразовывать химическую энергию окислительно-восстановительной реакции, происходящей в ней, в электрическую энергию. Электроды, которые составляют гальванический элемент, называются полуэлементами. Окислительно-восстановительная реакция, протекающая в гальваническом элементе, пространственно разделена. Полуреакция окисления происходит в полуэлементе, называемом анодом (отрицательно заряженный электрод), а полуреакция восстановления происходит на катоде.

Электродвижущая сила (ЭДС) гальванического элемента алгебраически состоит из различий во внутренних потенциалах составляющих его электродов. Поэтому, если электрод с известным значением разности внутренних потенциалов Me (Me) —  (раствор) принимается за один полуэлемент, то измеренное значение ЭДС можно использовать для расчета требуемой разности потенциалов изучаемый электрод.

Для этой цели обычно используют стандартный (нормальный) водородный электрод. Он состоит из платиновой пластины или проволоки, покрытой платиновой сажей (мелкая платина), погруженной в раствор кислоты с = 1 моль / л, давление водорода выше которого составляет 0,1 МПа (1 атм). Под каталитическим воздействием платиновой сажи в электроде происходит обратимый окислительно-восстановительный переход. Разница внутренних потенциалов для водородного электрода в соответствии с формулой Нернста составляет:

Ионы, от концентрации которых непосредственно зависит потенциал электрода, называются определяющими потенциал для данного электрода.

По природе определяющих потенциал ионов, есть I, II типа, окислительно-восстановительные электроды и мембранные электроды.

Электроды типа I включают металл, амальгаму и газ. Для них определяющими потенциал ионами являются катионы. Они обратимы по отношению к катионам.

Металлические электроды состоят из металла, погруженного в раствор, содержащий его ионы. Они могут быть представлены в виде диаграммы: MeZ + / Me, например Ag + / Ag. На них отвечает обратимый окислительно-восстановительный переход: MeZ + +  Me.

Видео:011 Электрохимия 4 уравнение НернстаСкачать

Газовые электроды состоят из инертного металла (обычно платины), контактирующего как с газом, так и с раствором, содержащим ионы этого газообразного вещества. Например, водородный электрод.

Электроды типа I обычно используются в EMA в качестве индикаторных электродов, то есть электродов, потенциал которых зависит от концентрации определенных ионов. Эта зависимость называется функцией электрода.

Электроды типа II состоят из металла, покрытого слоем его плохо растворимого соединения и погруженного в раствор растворимой соли, содержащей такой же анион, что и плохо растворимое соединение. Для них определяющими потенциал ионами являются анионы. Они обратимы по отношению к анионам.

Электроды типа II широко используются в электрохимических измерениях в качестве эталонов (электродов сравнения), поскольку их потенциал стабилен во времени и хорошо воспроизводится, если концентрация анионов поддерживается постоянной. Электроды Calomel и хлорид серебра чаще всего используются в качестве электродов сравнения.

Каломельный электрод состоит из ртути, покрытой пастой, содержащей каломель (Hg2Cl2), и в контакте с раствором KCl:

Cl- / Hg2Cl2, Hg; ½ Hg2Cl2 +  Hg + Cl-;
E (Cl- (Hg2Cl2, Hg)) = 0,2678-0,0257 ln (Cl-) при 298 К.

Обычно используются каломельные электроды с содержанием KCl 0,1 М; 1М и рассол.

При использовании насыщенного раствора потенциал хлорида серебра при 298 К составляет 0,22 В.

В мембранных (ионоселективных) электродах наиболее важным компонентом является полупроницаемая мембрана. Это тонкая жидкая или твердая пленка с преимущественной проницаемостью только для ионов одного типа (например, Na в присутствии ионов других щелочных металлов). Механизм полупроницаемости мембраны может быть различным. В некоторых случаях мембрана имеет поры определенного размера, через которые не проходят ионы больших размеров, в других случаях она изготовлена из материала, который растворяет одно из веществ, присутствующих в растворе, и, таким образом, обеспечивает его прохождение через мембрану. Часто материал мембраны представляет собой органический или неорганический ионообменник, матрица которого содержит ионные группы. Последние могут обменивать ионы в своем составе на другие ионы и тем самым обеспечивать прохождение последних через мембрану.

Пусть, например, ионообменная мембрана разделяет внутренний раствор № 2 иона А + с концентрацией С2 и внешний анализируемый раствор № 1 того же иона с концентрацией С1. В результате ионного обмена ион A + из внутреннего и внешнего растворов попадет в мембранную фазу. Разница в концентрации ионов A + в растворе и мембранной фазе приведет к появлению граничных потенциалов E1 и E2 на обеих поверхностях мембраны.

Основной проблемой, возникающей при использовании мембранных электродов в качестве индикаторных электродов, является их селективность (селективность). В идеальном случае функция электрода должна выражать зависимость только от определенного типа ионов АЗ +. Однако почти невозможно найти мембрану, через которую проходили только эти ионы. Как правило, другие ионы проходят через мембрану, влияя на ее потенциал. Селективность мембранного электрода обычно оценивают по коэффициенту селективности CA, V, который учитывает вклад посторонних ионов в величину потенциала электрода. Чем ниже К, тем меньше влияние посторонних ионов на мембранный потенциал, тем выше селективность мембранного электрода. С учетом коэффициента селективности значение мембранного потенциала рассчитывается по формуле Никольского.

В качестве индикаторных электродов используются только мембранные электроды с K 1, то относительно иона B. Для определения CA, B измеряется EM в растворах с постоянным содержанием B и уменьшением A. При некотором минимальном значении pa (A) линейный характер зависимости E = f (pa (A)) нарушается. Это означает, что потенциал электрода перестает зависеть от a (A), т.е. теряет свою электродную функцию от A и не различает ионы A и B. В точке пересечения линейных участков EA = EB и при ZA = ZB: a (A) / a (B) = KA, B. Чем меньше CA, B, тем выше селективность электрода по отношению к иону A.

Вывод:

Время отклика ионоселективного электрода характеризует время, необходимое для достижения постоянного потенциала электрода. Чем короче время отклика, тем лучше электрод. Может варьироваться от секунд до минут. Это зависит от природы мембраны и метода измерения (перенос электрода из разбавленного раствора в концентрированный или наоборот). Для большинства электродов потенциал находится в пределах 1 мин. достигает 90% от окончательного значения.

Решение IUPAC принято считать равным 0,00 В. Очевидно, что в этом случае измеренное значение ЭДС гальванического элемента, который включает водородный электрод, равно разности внутренних потенциалов второго электрода. Эту ЭДС обычно называют потенциалом электрода или окислительно-восстановительным потенциалом и обозначают буквой Е. Переход от внутренних потенциалов к окислительно-восстановительным потенциалам не меняет природу формулы Нернста.

Для большинства электродов значение потенциала электрода при отдельных активностях окисленной и восстановленной форм (E0) измеряется и приводится в справочниках.

При нормальных условиях и при переходе от натурального к десятичному логарифму пре-логарифмический фактор становится равным 0,0591, и формула принимает вид

Присылайте задания в любое время дня и ночи в ➔

Видео:Уравнение Нернста #shortsbetaСкачать

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.