Уравнение нернста для платинового электрода (2 видео)

Содержание

Уравнение нернста для платинового электрода
Уравнение Нернста. Потенциометрические методы анализа
Применение уравнения Нернста в решении задач.
Пример 1:
Решение:
Пример 2:
Решение:
🎬 Видео

Видео:Гальванические элементы. 1 часть. 10 класс.Скачать

Уравнение нернста для платинового электрода

ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ

Конспект лекций для студентов биофака ЮФУ (РГУ)

3.5 ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ

3.5.4 Классификация электродов

По типу электродной реакции все электроды можно разделить на две группы (в отдельную группу выделяются окислительно-восстановительные электроды, которые будут рассмотрены особо в разделе 3.5.5).

Электроды первого рода

К электродам первого рода относятся электроды, состоящие из металлической пластинки, погруженной в раствор соли того же металла. При обратимой работе элемента, в который включен электрод, на металлической пластинке идет процесс перехода катионов из металла в раствор либо из раствора в металл. Т.о., электроды первого рода обратимы по катиону и их потенциал связан уравнением Нернста (III.40) с концентрацией катиона (к электродам первого рода относят также и водородный электрод).

(III.40)

Электроды второго рода

Электродами второго рода являются электроды, в которых металл покрыт малорастворимой солью этого металла и находится в растворе, содержащем другую растворимую соль с тем же анионом. Электроды этого типа обратимы относительно аниона и зависимость их электродного потенциала от температуры и концентрации аниона может быть записана в следующем виде:

(III.48)

Для определения электродного потенциала элемента необходимо измерить ЭДС гальванического элемента, составленного из испытуемого электрода и электрода с точно известным потенциалом – электрода сравнения . В качестве примеров рассмотрим водородный, каломельный и хлорсеребряный электроды.

Водородный электрод представляет собой платиновую пластинку, омываемую газообразным водородом, погруженную в раствор, содержащий ионы водорода. Адсорбируемый платиной водород находится в равновесии с газообразным водородом; схематически электрод изображают следующим образом:

Электрохимическое равновесие на электроде можно рассматривать в следующем виде:

Потенциал водородного электрода зависит от активности ионов Н + в растворе и давления водорода; потенциал стандартного водородного электрода (с активностью ионов Н + 1 моль/л и давлением водорода 101.3 кПа) принят равным нулю. Поэтому для электродного потенциала нестандартного водородного электрода можно записать:

(III.49)

Каломельный электрод . Работа с водородным электродом довольно неудобна, поэтому в качестве электрода сравнения часто используется более простой в обращении каломельный электрод, величина электродного потенциала которого относительно стандартного водородного электрода точно известна и зависит только от температуры. Каломельный электрод состоит из ртутного электрода, помещенного в раствор КСl определенной концентрации и насыщенный каломелью Hg₂Сl₂:

Каломельный электрод обратим относительно анионов хлора и уравнение Нернста для него имеет вид:

(III.50)

Хлорсеребряный электрод . В качестве электрода сравнения используют также другой электрод второго рода – хлорсеребряный, представляющий собой серебряную проволоку, покрытую хлоридом серебра и помещённую в раствор хлорида калия. Хлорсеребряный электрод также обратим относительно анионов хлора:

Величина потенциала хлорсеребряного электрода зависит от активности ионов хлора; данная зависимость имеет следующий вид:

(III.51)

Чаще всего в качестве электрода сравнения используется насыщенный хлорсеребряный электрод, потенциал которого зависит только от температуры. В отличие от каломельного, он устойчив при повышенных температурах и применим как в водных, так и во многих неводных средах.

Электроды, обратимые относительно иона водорода, используются на практике для определения активности этих ионов в растворе (и, следовательно, рН раствора) потенциометрическим методом, основанном на определении потенциала электрода в растворе с неизвестным рН и последующим расчетом рН по уравнению Нернста. В качестве индикаторного электрода может использоваться и водородный электрод, однако работа с ним неудобна и на практике чаще применяются хингидронный и стеклянный электроды.

Хингидронный электрод , относящийся к классу окислительно-восстановительных электродов (см. ниже), представляет собой платиновую проволоку, опущенную в сосуд с исследуемым раствором, в который предварительно помещают избыточное количество хингидрона С₆Н₄О₂·С₆Н₄(ОН)₂ – соединения хинона С₆Н₄О₂ и гидрохинона С₆Н₄(ОН)₂, способных к взаимопревращению в равновесном окислительно-восстановительном процессе, в котором участвуют ионы водорода:

Хингидронный электрод является т.н. окислительно-восстановительным электродом (см. разд. 3.5.5); зависимость его потенциала от активности ионов водорода имеет следующий вид:

(III.52)

Стеклянный электрод , являющийся наиболее распространенным индикаторным электродом, относится к т.н. ионоселективным или мембранным электродам. В основе работы таких электродов лежат ионообменные реакции, протекающие на границах мембран с растворами электролитов; ионоселективные электроды могут быть обратимы как по катиону, так и по аниону.

Принцип действия мембранного электрода заключается в следующем. Мембрана, селективная по отношению к некоторому иону (т.е. способная обмениваться этим ионом с раствором), разделяет два раствора с различной активностью этого иона. Разность потенциалов, устанавливающаяся между двумя сторонами мембраны, измеряется с помощью двух электродов. При соответствующем составе и строении мембраны её потенциал зависит только от активности иона, по отношению к которому мембрана селективна, по обе стороны мембраны.

Наиболее часто употребляется стеклянный электрод в виде трубки, оканчивающейся тонкостенным стеклянным шариком. Шарик заполняется раствором НСl с определенной активностью ионов водорода; в раствор погружен вспомогательный электрод (обычно хлорсеребряный). Потенциал стеклянного электрода с водородной функцией (т.е. обратимого по отношению к иону Н + ) выражается уравнением

(III.53)

Необходимо отметить, что стандартный потенциал ε °_ст для каждого электрода имеет свою величину, которая со временем изменяется; поэтому стеклянный электрод перед каждым измерением рН калибруется по стандартным буферным растворам с точно известным рН.

3.5.5 Окислительно-восстановительные электроды

В отличие от описанных электродных процессов в случае окислительно-восстановительных электродов процессы получения и отдачи электронов атомами или ионами происходят не на поверхности электрода, а только в растворе электролита. Если опустить платиновый (или другой инертный) электрод в раствор, содержащий двух- и трехзарядные ионы железа и соединить этот электрод проводником с другим электродом, то возможно либо восстановление ионов Fe 3+ до Fe 2+ за счет электронов, полученных от платины, либо окисление ионов Fe 2+ до Fe 3+ с передачей электронов платине. Сама платина в электродном процессе не участвуют, являясь лишь переносчиком электронов. Такой электрод, состоящий из инертного проводника первого рода, помещенного в раствор электролита, содержащего один элемент в различных степенях окисления, называется окислительно-восстановительным или редокс-электродом . Потенциал окислительно-восстановительного электрода также определяют относительно стандартного водородного электрода:

Pt, H₂ / 2H + // Fe 3+ , Fe 2+ / Pt

Зависимость потенциала редокс-электрода ε _RO от концентрации (активности) окисленной [Ox] и восстановленной форм [Red] для окислительно-восстановительной реакции, в которой не участвуют никакие другие частицы, кроме окислителя и восстановителя, имеет следующий вид (здесь n – число электронов, участвующих в элементарном акте окислительно-восстановительной реакции):

(III.54)

Из данного выражения следует уравнение для потенциала металлического электрода (III.40), т.к. активность атомов металла (восстановленной формы) в материале электрода равна единице.

В случае более сложных систем в выражении для окислительно-восстановительного потенциала фигурируют концентрации всех участвующих в реакции соединений, т.е. под окисленной формой следует понимать все соединения в левой части уравнения реакции

а под восстановленной – все соединения в правой части уравнения. Так, для окислительно-восстановительных реакций, протекающих с участием ионов водорода

уравнение Нернста будет записываться следующим образом:

(III.55)

При составлении гальванических элементов с участием редокс-электрода электродная реакции на последнем в зависимости от природы второго электрода может быть либо окислительной, либо восстановительной. Например, если составить гальванический элемент из электрода Pt / Fe 3+ , Fe 2+ и второго электрода, имеющего более положительный электродный потенциал, то при работе элемента редокс-электрод будет являться анодом, т.е. на нем будет протекать процесс окисления:

Если потенциал второго электрода будет меньше, чем потенциал электрода Pt / Fe 3+ , Fe 2+ , то на последнем будет протекать реакция восстановления и он будет являться катодом:

Знание величин электродных потенциалов позволяет определить возможность и направление самопроизвольного протекания любой окислительно-восстановительной реакции при одновременном наличии в растворе двух или более окислительно-восстановительных пар. Восстановленная форма любого элемента или иона будет восстанавливать окисленную форму другого элемента или иона, имеющего более положительный электродный потенциал.

Видео:Электродные потенциалы металлов. Электроды сравненияСкачать

Уравнение Нернста. Потенциометрические методы анализа

Потенциометрические методы основаны на измерении электродвижущих сил (ЭДС):

где E — электродвижущая сила (ЭДС);
E₁ и E₂ — потенциалы электродов исследуемой цепи.

Потенциал электрода E связан с активностью и концентрацией веществ, участвующих в электродном процессе, уравнением Нернста:

где E0 — стандартный потенциал редокс-системы;
R — универсальная газовая постоянная, равная 8,312 Дж/(моль К);
T — абсолютная температура, К;
F — постоянная Фарадея, равная 96485 Кл/моль;
n — число электронов, принимающих участие в электродной реакции;
a_ox, a_red — активности соответственно окисленной и восстановленной форм редокс-системы;
[ox], [red] — их молярные концентрации;
Г_ox, Г_red — коэффициенты активности.

E=E₀ при a_ox = a_red = 1, причем имеется в виду гипотетический стандартный 1 М раствор, в котором коэффициент активности каждого растворенного вещества равен 1, а чистые вещества находятся в наиболее устойчивом физическом состоянии при данной температуре и нормальном атмосферном давлении.

Подставляя T=298,15 и числовые значения констант в уравнение, получаем для 25 °C

Однако потенциал отдельного электрода экспериментально определить невозможно. Относительные значения электродного потенциала находят, комбинируя данный электрод со стандартным водородным электродом, который является общепринятым международным стандартом. Потенциал водородного электрода принят равным нулю при всех температурах, поэтому потенциал данного электрода — это, в сущности, ЭДС элемента, состоящего из данного и стандартного водородного электрода.

Конструктивно стандартный водородный электрод представляет собой платинированную платиновую пластинку, омываемую газообразным водородом при давлении 1,013 . 10 5 Па (1 атм) и погруженную в раствор кислоты с активностью ионов H + , равной единице. При работе водородного электрода протекает реакция

В практической работе вместо хрупкого и нередко капризного водородного электрода применяют специальные, более удобные в работе стабильные электроды сравнения, потенциал которых по отношению к стандартному водородному электроду точно известен.

Уравнение (2) можно переписать

Величину E₀‘ называют формальным потенциалом. Как видно, формальный потенциал характеризует систему, в которой концентрации (а не активности) всех участников равны 1,0 моль/л. Формальный потенциал включает в себя коэффициенты активности, т.е. зависит от ионной силы раствора. Если коэффициент активности равен 1, то E₀‘=E₀, т.е. формальный потенциал совпадает со стандартным. Точность такого приближения для многих расчетов оказывается достаточной.

Природа возникновения потенциала различна. Можно выделить следующие три основные классы потенциалов, которые не исчерпывают, конечно, всего многообразия. Это:

Электродные потенциалы.
Редокс-потенциалы.
Мембранные потенциалы.

Хотя по термином «электродный потенциал» нередко имеют в виду любой потенциал, независимо от механизма его возникновения, в более узком понимании — это потенциал непосредственно связанный с материалом электрода. Например, цинковый электрод:

Активность свободного металла принимается равной единице. Электродные потенциалы отличаются от редокс-потенциалов, для которых материал электрода не имеет значения, так как они химически инертны по отношению ко всем веществам в растворе, и от мембранных, для которых разность потенциалов на мембране измеряется с помощью пары других (в принципе, возможно, одинаковых) электродов.

Потенциометрические методы анализа известны с конца прошлого века, когда Нернст вывел (1889) известное уравнение (1), а Беренд сообщил (1883) о первом потенциометрическом титровании. Интенсивное развитие потенциометрии в последние годы связано, главным образом, с появлением разнообразных типов ионоселективных электродов, позволяющих проводить прямые определения концентрации многих ионов в растворе, и успехами в конструировании и массовом выпуске приборов для потенциометрических измерений.

Потенциометрические методы анализа подразделяют на прямую потенциометрию (ионометрию) и потенциометрическое титрование. Методы прямой потенциометрии основаны на прямом применении уравнения Нернста (1) для нахождения активности или концентрации участника электродной реакции по экспериментально измеренной ЭДС цепи или потенциалу соответствующего электрода. При потенциометрическом титровании точку эквивалентности определяют по резкому изменению (скачку) потенциала вблизи точки эквивалентности.

Васильев В. П. Аналитическая химия. В 2 кн. Кн. 2. Физико-химические методы анализа: Учеб. для студ. вузов, обучающихся по химико-технол. спец. — 2-е изд., перераб. и доп. — М.:Дрофа, 2002. — 384 с., ил. — С. 179-181.

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

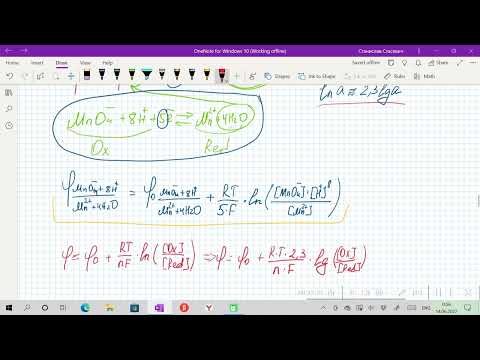
Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи: