Уравнение нернста для пары io3 i (6 видео)

Аналитическая химия. Расчеты в методе редоксиметрии. Методические указания и варианты контрольных заданий к самостоятельной работе по дисциплине «Аналитическая химия и ФХМА»для студентов II курса ХТФ направления 240100– «Химическая технология и биотехнология»

Содержание

УДК 543.24(076.5)
Рекомендуемая литература
Применение уравнения Нернста в решении задач.
Пример 1:
Решение:
Пример 2:
Решение:
Окислительно-восстановительные процессы в анализе
📺 Видео

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

Томский политехнический университет

УТВЕРЖДАЮ

Расчеты в методе редоксиметрии.

Методические указания и варианты контрольных заданий

к самостоятельной работе по дисциплине

«Аналитическая химия и ФХМА»для студентов II курса ХТФ

направления 240100– «Химическая технология и биотехнология»

Томского политехнического университета

УДК 543.24(076.5)

Аналитическая химия. Расчеты в методе редоксиметрии. Ме-

А 545 тодические указания и варианты контрольных заданий к самостоятельной работе по дисциплине «Аналитическая химия» для студентов II курса ХТФ направления 240100– «Химическая технология и биотехнология» /сост. . , – Томск.: Изд-во Томского политехнического университета, 2009. – 32 с.

Методические указания, варианты контрольных заданий

рассмотрены и рекомендованы к изданию методическим семинаром

кафедры физической и аналитической химии ХТФ

Зав. кафедрой д. х.н.,

методической комиссии _____________

Кандидат химических наук, доцент

политехнического университета, 2009

Расчеты в методе редоксиметрии

В данном методическом указании приводятся примеры упрощенных расчетов в окислительно-восстановительных системах. Приведены некоторые примеры расчета потенциала в смесях окислителей и восстановителей, скачка на кривых титрования и обоснования выбора индикатора, показано, как оценить возможное направление окислительно-восстановительной реакции и степень (полноту) ее протекания.

1. Расчет Е для редокс-пары вещества.

Для разбавленных растворов зависимость реальных (равновесных) потенциалов от природы реагирующих веществ, их концентрации, температуры и других факторов описывается уравнением Нернста:

(1)

где Е – реальный (равновесный) окислительно-восстановительный потенциал данной пары, В; ЕO – стандартный окислительно-вос-становительный потенциал, В; [Ox] и [Red] – равновесные концентрации окисленной и восстановленной форм, моль/л; R – универсальная газовая постоянная, равная 8,314 Дж/К. моль; Т – абсолютная температура, К; F – число Фарадея, равное 96500 Кл/моль; z – число электронов, участвующих в полуреакции; а и b – стехиометрические коэффициенты.

Пример 1. Записать уравнение Нернста для следующих полуреакций:

а) Сr2O72– + 14H+ + 6е → 2Cr3+ +7H2O б) 2Cl– –2е → Cl2↑

в) Zn2+ + 2е → Zn0 г) H2O2 +2H+ + 2е →2H2O

Решение. а) поскольку в полуреакции участвуют ионы водорода, их концентрация входит в уравнение Нернста в степени, равной стехиометрическому коэффициенту:

б, в, г) в случае, когда один из компонентов редокс-пары представляет собой практически нерастворимое в воде вещество, газ или малодиссоциирующее соединение, концентрация его является величиной постоянной, т. е. входит в величину ЕO, и потому не учитывается в уравнении Нернста.

С учетом этого уравнение Нернста для соответствующих полуреакций имеет вид:

(б);

(в);

(г)

Пример 2. Вычислить значение потенциала системы

MnO4– +8H+ + 5е → Mn2+ +4H2O при pH 1 и pH 5, учитывая, что [MnO4–] = [Mn2+] = 1 моль/л.

Решение. Уравнение Нернста для данной полуреакции имеет вид:

Учитывая, что [H+] = 10–pH := 10–1 моль/л, вычислим значение потенциала при рН 1:

= 1,42 В.

Аналогично, при рН 5:

= 1,04 В.

2. Определение направления окислительно-восстановительных процессов.

Окислительно-восстановительная реакция будет протекать в прямом направлении только в том случае, если электродвижущая сила реакции (э. д.с.), вычисляемая как , имеет положительное значение, причем, чем больше э. д.с., тем интенсивнее протекает реакция; – стандартные окислительно-восстановительные потециалы редокс-пар окислителя и восстановителя, соответственно.

Пример 1. Определить, в каком направлении и с какой интенсивностью пойдут следующие реакции:

а) Fe2+ + F2 Fe3+ + 2F– б) Fe2+ + Cl2 Fe3+ + 2Cl–

в) Fe2+ + Br2 Fe3+ + 2Br– г) Fe2+ + I2 Fe3+ + 2I–

Решение. Сопоставим значения ЕO окислительно-восстановительных пар:

= + 0,77 В; = +2,77 В; = + 1,36 В; = = +1,08 В; = +0,54 В. Видно, что окислить Fe 2+-ионы до Fe 3+ можно действием F2 , Cl2 и Br2. Вычислим э. д.с. реакций:

а) 2,77 – 0,77= 2,00 В; в) 1,36 – 0,77= 0,59 В; c) 1,08 – 0,77 = 0,31 В.

Наиболее сильно выражена окислительная способность у молекул F2 , менее всего – у Br 2 . Ионы Fe 2+ нельзя окислить действием I2 , т. к. значение э. д.с. отрицательно: 0,54 – 0,77 = – 0,23 В. Реакция будет протекать в направлении восстановления ионов Fe 3+ иодид-ионами:

Fe3+ + 2I– → Fe2+ + I2

Пример 2.Определить, какая реакция будет протекать в первую очередь, если на раствор SnCl4 подействовать металлическим железом:

а) Fe + Sn4+ → Fe2+ + Sn2+ , б) Fe + Sn4+ → Fe2+ + Sn?

= – 0,44 В; = + 0,15 В; = + 0,01 В

Решение. Э. д.с. реакций: а) 0,15 – (–0,44) = + 0,59 В; б) 0,01 – (–0,44) = +0,45 В. Так как в первую очередь протекает тот процесс, которому соответствует наибольшая разность стандартных редокс-потенциа-
лов, пойдет реакция восстановления Sn 4+ до Sn 2+, т. е. реакция а).

3. Расчет Е в растворах различных смесей окислителей и восстановителей

При сливании растворов окислителя и восстановителя окислительно-восстановительный потенциал полученной смеси зависит от количеств взятых окислителя и восстановителя и рН раствора, если окислительно-восстановительная реакция протекает с участием Н+ – или ОН– –ионов.

Пример 1. Вычислить значение Е раствора, полученного при сливании 10 мл 0,1 н раствора Sn2+ c: а) 8,0 мл 0,1 н раствора KBrO3; б) 10,0 мл 0,1 н раствора KBrO3; в) 20,0 мл 0,1 н раствора KBrO3, если рН =0.

Решение. Окислительно-восстановительный потенциал системы рассчитывают по уравнению Нернста для редокс-пары вещества, взятого в избытке. Первоначально рассчитывают количество миллиэквивалентов взятых окислителя и востановителя (nOx, nRed, мэкв) до реакции. Затем рассчитывают количество окислителя и восстановителя в растворе после проведения реакции и вычисляют Е системы. Уравнения полуреакций:

Sn 2+ + 2e → Sn 4+ ; BrO3– + 6H+→ Br – +3H2O,

а) рассчитываем количество окислителя и восстановителя до реакции:

n(Sn 2+ ) = СнV = 0.1 10×= 1 мэкв; n(BrO3– ) = 0.1 8×= 0,8 мэкв

Рассчитываем количество веществ после проведения реакции:

n(Sn 2+ ) = 1 – 0,8 = 0,2 мэкв; n(Sn 4+ ) = 0,8 мэкв; n(BrO3– ) = 0

Т. о., после проведения реакции в растворе останется редокс-пара Sn4+/Sn 2+, которая будет определять Е раствора:

Отношение концентраций Sn4+/Sn 2+ равно отношению их количеств (мэкв), поскольку стехиометрические коэффициенты окисленной и восстановленной форм в соответствующей полуреакции одинаковы.

б) рассчитываем количество окислителя и востановителя до реакции:

n(Sn 2+ ) = СнV = 0.1 10×= 1 мэкв; n(BrO3– ) = 0.1 10×= 1 мэкв

Вещества взяты в эквивалентных количествах, следовательно, потенциал системы вычисляют по уравнению:

(2)

Тогда

в) рассчитываем количество окислителя и восстановителя до реакции:

n(Sn 2+ ) = СнV = 0.1 10×= 1 мэкв; n(BrO3– ) = 0.1 20×= 2 мэкв

Рассчитываем количество веществ после проведения реакции:

n(Sn 2+ ) =0; n(Sn 4+ ) = 1 мэкв; n(BrO3– ) = 2 – 1 = 1 мэкв; ; n(Br – ) = 1 мэкв. Т. о., после проведения реакции в растворе останется редокс-пара BrO3– / Br – , которая будет определять Е раствора:

Пример 2. Расcчитать скачок на кривой титрования 10,0 мл 0,1 н раствора FeSO4 0,1 н раствором Ce(SO4)2 в сернокислой среде, погрешность титрования принять равной 0,1%.

Решение. При титровании протекает следующая реакция:

Fe2+ + Сe4+ → Fe3+ + Ce3+

(= +0,77 В; = +1,44 В)

1. Расчет потенциала до точки эквивалентности

В процессе титрования до точки эквивалентности в растворе имеется избыток определяемого вещества, следовательно, потенциал системы рассчитываем по формуле (1) для пары Fe3+/Fe2+:

При этом , а

Тогда, при добавлении 0,1 мл 0,1 н раствора Ce(SO4)2 потенциал системы будет равен:

= 0,71 В

При добавлении 5,0 мл 0,1 н раствора Ce(SO4)2 :

= 0,77 В и т. д.

К моменту начала скачка добавлено (Vэкв – 0,1%), т. е. 9,99 мл титранта, поскольку = 10 мл, а 0,1% от этого объема составляет 0,01 мл. Тогда

= 0,95 В.

В данном случае стехиометрические коэффициенты у окисленной и восстановленной форм в полуреакциях одинаковы, поэтому отношение равновесных концентраций [Ox]/[Red] можно заменить отношением их количеств, выраженным в процентах. При этом расчет ЕН. С. значительно упрощается. Действительно, к моменту начала скачка в растворе осталось неоттитрованным 0,1% Fe2+ и образовалось 99,9% Fe3+, тогда:

= 0,95 В.

2. Расчет потенциала в точке эквивалентности

В точке эквивалентности к 10,0 мл 0,1 н раствора FeSO4 прибавлено 10,0 мл 0,1 н раствора Ce(SO4)2 .

= 1,11 В

3. Расчет потенциала после точки эквивалентности

После точки эквивалентности в растворе в избытке находится титрант, поэтому потенциал раствора рассчитываем по формуле (1) для пары Ce4+/Ce3+:

При добавлении титранта Ce(SO4)2 после точки эквивалентности: ,

а .

К моменту конца скачка, при добавлении 10,01 мл 0,1 н раствора Ce(SO4)2, т. е. (Vэкв + 0,1%), потенциал системы будет равен:

= 1.27 В

Вычислим значение ЕК. С. с учетом того, что избыток Ce4+ к этому моменту составляет 0,1%, а количество образовавшегося Ce3+ – 100%:

= 1,27 В.

При добавлении 10,10 мл 0,1 н раствора Ce(SO4)2 получим:

= 1,33 В и т. д.

Пример 3. Какому математическому выражению соответствует окислительно-восстановительный потенциал системы, оттитрованной на 70%, если титрант – КМnO4 , а [H+] = 1 моль/л?

5H3AsO3 + 2KMnO4 + 3H2SO45H3AsO4 + 2MnSO4 + K2SO4 +3H2O,

(а) (б)

(в) (г)

Решение. Уравнение данной реакции можно представить следующими полуреакциями:

AsO33– + H2O – 2е →AsO43– + 2Н+ и

MnO4– +8H+ + 5е → Mn2+ +4H2O

Прореагировало лишь 70% определяемого вещества, в растворе имеется его избыток, следовательно, потенциал системы рассчитываем по уравнению (1) для редокс-пары AsO43–/ AsO33–. В данном случае стехиометрические коэффициенты у окисленной и восстановленной форм в полуреакциях одинаковы, поэтому отношение равновесных концентраций [Ox]/[Red] равно отношению их количеств. Количество AsO33– , оставшегося в растворе, составляет 30%, количество образовавшегося AsO43– – 70%. Учитывая, что = – 0,56 В, для описания окислительно-восстановительного потенциала системы следует выбрать выражение (г).

4. Расчет константы равновесия окислительно-восстановительных реакций.

Пример 1. Исходя из константы равновесия, предсказать вероятность окисления CuS и HgS азотной кислотой:

а) 3CuS + 8HNO3 3S + 3Cu(NO3)2 +2NO + 4H2O

б) 3HgS + 8HNO3 3S + 3Hg(NO3)2 +2NO + 4H2O

+ 0,60 B; +0,96B;

+ 1,04 B;

Решение. Находим константу равновесия реакции согласно уравнению (3):

(3),

где К — константа равновесия реакции;

– стандартные потенциалы окислителя и восстановителя;

n – наименьшее общее кратное числу электронов, отданных восстановителем и принятых окислителем.

а) , откуда К = 1036.

Большая величина константы показывает, что равновесие этой реакции практически полностью сдвинуто вправо, следовательно CuS хорошо растворяется в азотной кислоте.

б) ,откуда К = 10–8.

Малая величина константы означает, что равновесие этой реакции практически полностью сдвинуто влево, т. е. HgS в противоположность сульфиду меди практически нерастворим в азотной кислоте.

Пример 2. Какому из математических выражений соответствует формула для расчета lgK окислительно-восстановительной реакции

3Ti2(SO4)3 + K2Cr2O7+ 7H2SO4 6Ti(SO4)2 + Cr2(SO4)3 +K2SO4 +H2O,

(а) (б)

(в) (г)

Решение. Уравнение данной реакции можно представить следующими полуреакциями:

Сr2O72– + 14H+ + 6е → 2Cr3+ +7H2O

С учетом того, что 1,33 В, 0,09 В, n = 6,

согласно соотношению (3), значение lgK следует рассчитывать по выражению (г).

Видео:Уравнение Нернста. Условия изменения направления ОВР. Продукты в ОВР. Ч.5-3.Скачать

Рекомендуемая литература

Васильев химия. Ч 1.– М.: Дрофа, ч–368 с.

2. Основы аналитической химии. Т 1. /Под ред. .– М.: Высшая школа, 2001.– 486 с.

1. , Пятницкий химия. — М.: Химия, ч.1 – 1990. – 480 с.

4. . Аналитическая химия. Аналитика. т.1 — М.: Высшая школа, 2001. – 615 с.

5. Цитович аналитической химии. – М.: Высшая школа, 1994. – 495 с.

6. , Эфрос по количественному анализу.– Л.: Химия, 1986.– 160с.

7. Лурье по аналитической химии. 6-е изд., перераб. и доп.– М.: Химия, 1989.– 448с.

8. Алексеев анализ. – М.: Химия, 1972.– 504 с.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HCl + MnO2 ® Cl2 + MnCl2 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Можно ли окислить ионы SO3 2– действием J2? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы, полученной при смешивании 10,0 мл 0,1 н раствора Sn2+ и а) 9,98 мл 0,1 н раствора KBrO3, б) 10,0 мл 0,1 н раствора KBrO3, в) 10,02 мл 0,1 н раствора KBrO3; во всех случаях рН = 0.

4. Чему равен титр раствора перманганата калия по нитриту натрия, если на титрование 10,0 мл 0,05 н раствора NaNO2 в кислой среде в среднем расходуется 5,50 мл раствора КMnO4?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

K2Cr2O7 + KI + H2SO4 ® Cr2(SO4)3 +I2 + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Вычислить окислительно-восстановительный потенциал системы:

Na2SO3 + KMnO4 + H2SO4 ® Na2SO4 + MnSO4 + K2SO4 +H2O,

оттитрованной на а) 99,8%, б) 100%, в) 100,2% ,если исходные концентрации веществ одинаковы, титрантом служит KMnO4, [H+] = 1 моль/л?

3. Вычислить константу равновесия реакции, оценить степень обратимости и направление реакции:

KClO3 + J2 + H2O →HClO4 + KJ

4. Рассчитать массу навески руды, содержащей 40% железа, чтобы на титрование раствора, полученного при растворении ее и восстановлении железа до Fe(2+), расходовалось 15,0 мл 0,10 н раствора KMnO4 (среда кислая).

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

J2 + Na2S2O3 ® NaJ + Na2S4O6

Записать уравнение Нернста для редокс-пары восстановителя.

2. Можно ли действием KMnO4 в нейтральной среде окислить NO2–ионы? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы

Ti2(SO4)3 + KBrO3 + 3H2SO4 ® Ti(SO4)2 + KBr + H2O,

если раствор Ti2(SO4)3 а) недотитрован на 0,1%, б) перетитрован на 0,1%. в) оттитрован на 100%. Титрант – KBrO3, концентрации реагирующих веществ одинаковы, [H+] = 1 моль/л.

4. Определить массовую долю олова (II) в бронзе, если на титрование раствора, полученного из 0,8245 г бронзы, израсходовано 12,75 мл 0,05 н раствора иода.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

Cr2O3 + KNO3 + KOH ® K2CrO4 +KNO2 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Будут ли окисляться ионы Ti 3+ под действием бромата калия KBrO3 в кислой среде? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы,

H3AsO3 + KMnO4 + H2SO4® H3AsO4 + MnSO4 + K2SO4 + H2O,

оттитрованной на а) 99,8%, б) 100%, в) 100,2% ,если исходные концентрации веществ одинаковы, титрант – КМnO4 , [H+] = 1 моль/л?

4. К 25,0 мл бромной воды прибавили избыток раствора иодида калия. На титрование выделившегося йода израсходовано 20,00 мл 0,1 н раствора Na2S2O3 . Определить содержание Br2 в 1 литре бромной воды.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KNO2 + KI + H2SO4 ® I2 +NO + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Вычислить окислительно-восстановительный потенциал системы, если раствор а) недотитрован на 0,1%, б) перетитрован на 0,1%. в) оттитрован на 100%; исходные концентрации веществ одинаковы, титрант – KBrO3, [H+] = 1 моль/л?

SnCl2 + KBrO3 + HCl ® SnCl4 + KBr + H2O

3. Будут ли окисляться ионы Mn 2+ под действием дихромата калия в кислой среде? Вычислить константу равновесия реакции.

4. Какую навеску K2Cr2O7 нужно взять для установления титра

0,1 н раствора Na2S2O3, если располагают мерной колбой объемом 200,0 мл, пипеткой вместимостью 10,0 мл и стремятся к тому, чтобы на титрование выделенного йода расходовалось не более 25,00 мл тиосульфата натрия?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KMnO4 + H3AsO3 + H2SO4 ® H3AsO4 + MnSO4 + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Будут ли окисляться ионы S 2– под действием йода J2? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы, состоящей из 5,0 мл 0,02 н Н2О2 и а) 10,0 мл 0,02 н KMnO4, б) 4,0 мл 0,02 н KMnO4 , [H+] = 1 моль/л?

4. Определить массу Mn 2+ в растворе, если на титрование до MnO2 в слабощелочной среде затрачено 21,20 мл 0,1010 н раствора KMnO4:

Mn 2+ + MnO4 – + ОН – ® MnO2 + H2O

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KMnO4 + NaBr + H2O ® Br2 + MnO2¯ + NaOH + KOH

Записать уравнение Нернста для редокс-пары окислителя.

2. Определить направление и полноту протекания реакции. Вычислить константу равновесия реакции.

Sn 4+ + Fe 2+® Sn 2+ + Fe 3+

3. Рассчитать скачок на кривой титрования 10,0 мл 0,02 н раствора Fe2+ 0,02 н раствором бромата калия, приняв погрешность титрования равной ± 0,1%, а рН = 0.

4. Вычислить содержание С12 в 1 литре хлорной воды, если к 25,0 мл хлорной воды прибавили раствор иодида калия и на титрование выделившегося иода израсходовали 20,00 мл 0,05 н раствора Na2S2O3.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

K2Cr2O7 + FeSO4 + H2SO4 ® Cr2(SO4)3 +Fe2(SO4)3 +K2SO4 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Определить направление и полноту протекания реакции. Вычислить константу равновесия реакции.

MnSO4 + CO2↑ + K2SO4 + H2O→ H2C2O4 + KMnO4 + H2SO4

3. Вычислить окислительно-восстановительный потенциал смеси, состоящей из 10,0 мл 0,1 н раствора NaNO2 и а) 8,0 мл 0,1 н раствора KMnO4, б) 10,0 мл 0,1 н раствора KMnO4, в) 12,0 мл 0,1 н раствора KMnO4, [H+] = 1 моль/л?

4. Вычислить %-ное содержание воды в кристаллогидрате H2C2O4·хH2O, если известно, что на титрование навески щавелевой кислоты массой 0,0342 г израсходовано 15,40 мл 0,035 н раствора КМnO4.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

Na2SO3 + KMnO4 + H2SO4 → MnSO4 + Na2SO4 + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Будут ли окисляться ионы AsO2 – под действием бромата калия KBrO3 в кислой среде? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы

Sn 2+ + MnO4 – + H + → Sn 4+ + Mn 2+ + H2O,

когда раствор а) недотитрован на 0,1%, б) перетитрован на 0,1%. в) оттитрован на 100%. Титрант – KMnO4, [H+] = 1 моль/л, исходные концентрации веществ одинаковы.

4. Навеску сплава растворили без доступа воздуха в серной кислоте. Образовавшуюся соль FeSO4 оттитровали 13,40 мл раствора KBrO3 с титром 0,002783 г/мл. Сколько граммов железа (II) содержалось в навеске сплава?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HNO3 + H2S ® NO +S¯ + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Будет ли дихромат калия в кислой среде окислять ионы Br –? Вычислить константу равновесия реакции.

3. Рассчитать скачок на кривой титрования для 10 мл 0,05 н раствора Na2SO3 с погрешностью ±0,2% .Титрант – 0,05 н раствор KMnO4, [H+] = 1 моль/л?

4. Вычислить молярную концентрацию эквивалента раствора KMnO4, если на титрование навески соли FeSO4 массой 0,1000 г, содержащей 0,1% индифферентных примесей, израсходовано 14,50 мл раствора KMnO4. Титрование вели в сернокислой среде.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

H2C2O4 + KMnO4 + H2SO4 ® MnSO4 + K2SO4 + CO2 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Можно ли действием J2 окислить ионы AsO2 – ? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы, если раствор SnCl2 а) недотитрован на 0,1%, б) оттитрован на 100%, в) переитрован на 0,1% . Титрант – бромат калия KBrO3, исходные концентрации реагирующих веществ одинаковы, [H+] = 1 моль/л.

4. На титрование навески щавелевой кислоты H2C2O4·2H2O массой 0,0630 г затрачено 20,00 мл раствора перманганата калия. Чему равны концентрация раствора KMnO4, моль-экв/л, и его титр?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

H2S + HNO3 ® H2SO4 + NO2 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Будет ли перманганат калия окислять ионы Ce 3+в кислой среде? Вычислить константу равновесия реакции.

3. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора Fe2+ 0,05 н раствором бромата калия, если принять погрешность титрования, равной ±0,1%, а рН = 0.

4. Для установки титра

0,1 н раствора тиосульфата натрия методом отдельных навесок взяли 0,1190 г K2Cr2O7 . Можно ли использовать эту навеску, если объем бюретки 50,0 мл? Ответ доказать расчетом.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

Cl2 + KOH ® KCl +KClO3 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Можно ли действием K2Cr2O7 в кислой среде окислить ионы S 2–? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы, полученной смешиванием 10,0 мл 0,2 н раствора FeSO4 и а) 12,0 мл 0,12 н раствора KMnO4, б) 20,0 мл 0,12 н раствора KMnO4, рН = 0?

4. Определить %-ное содержание воды в кристаллогидрате соли Мора (NH4)2Fe(SO4)2·хH2O, если на титрование навески массой 0,4250 г затрачено 25,50 мл 0,05 н раствора KMnO4?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

Na2SO3 + I2 + H2O ® Na2SO4 + HI

Записать уравнение Нернста для редокс-пары восстановителя.

2. Будут ли окисляться ионы Br – под действием перманганата калия в кислой среде? Вычислить константу равновесия реакции.

3. Рассчитать массу навески руды, содержащей около 60% Fe2O3, чтобы на титрование Fe 2+ , полученного при ее обработке, расходовалось бы 12,45 мл 0,1 н раствора KMnO4 .

4. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора Na2S2O3 0,05 н раствором J2, если принять погрешность титрования, равной ±0,1%, а рН = 2.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KMnO4 + H2O2 + H2SO4 ® MnSO4 +O2 +K2SO4 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Вычислить константу равновесия, оценить полноту протекания и направление реакции:

Na3AsO3 + KMnO4 + H2SO4 ® Na3AsO4 + MnSO4 + K2SO4 + H2O

3. Вычислить окислительно-восстановительный потенциал системы, состоящей из 10,0 мл 0,1 н раствора FeSO4 и а) 8,0 мл 0,1 н раствора KBrO3, б) 10,0 мл 0,1 н раствора KBrO3, в) 12,0 мл 0,1 н раствора KBrO3, рН = 0?

4. При определении концентрации раствора щавелевой кислоты 50,0 мл его разбавили в мерной колбе до 200,0 мл, затем отобрали аликвотную часть в 10,0 мл, на титрование которой израсходовали 11,25 мл 0,1090 н раствора дихромата калия. Вычислить молярную концентрацию исходного раствора Н2C2O4 .

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

Na2S2O3 + I2 + NaOH ® Na2SO4 + NaI + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Можно ли действием J2 окислить ионы NO2 –? Вычислить константу равновесия реакции.

3. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора Na3AsO3 0,05 н раствором J2, если принять погрешность титрования, равной ±0,1%, а реакция проводится при рН = 0?

Na3AsO3 + J2 + H2O ® Na3AsO4 + HJ,

4. Для установки титра

0,05 н раствора тиосульфата натрия методом отдельных навесок взяли 0,1190 г K2Cr2O7. Можно ли использовать эту навеску, если объем бюретки 25,0 мл? Ответ доказать расчетом.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KBrO3 + KI + H2SO4 ® K2SO4 + KBr + I2 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Вычислить окислительно-восстановительный потенциал системы, состоящей из 10,0 мл 0,1 н раствора FeSO4 и а) 12,0 мл 0,1 н раствора KMnO4 , б) 6 мл 0,1 н раствора при рН =0?

3. Можно ли окислить действием K2Cr2O7 в кислой среде ионы AsO2 –? Вычислить константу равновесия реакции.

4. К 20,0 мл бромной воды прибавили раствор иодида калия. На титрование выделившегося йода израсходовано 24,45 мл 0,05 н раствора Na2S2O3 . Определить содержание Br2 в 1 литре бромной воды.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

CrCl3 + (NH4)2S2O8 + H2O ® (NH4)2Cr2O7 + NH4Cl + H2SO4 + HCl

Записать уравнение Нернста для редокс-пары окислителя.

2. Будут ли окисляться ионы F– под действием бромата калия KBrO3 в кислой среде? Вычислить константу равновесия реакции.

3. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора Н3AsO3 0,05 н раствором КМnO4, если принять погрешность титрования, равной ±0,1%, а реакция проводится при рН = 0?

H3AsO3 + KMnO4 + H2SO4 ® H3AsO4 + MnSO4 + K2SO4 + H2O

4. Рассчитать массу навески дихромата калия для установки титра

0,1 н раствора Na2S2O3 методом отдельных навесок, чтобы на титрование расходовалось не более 25,0 мл Na2S2O3? М(K2Cr2O7) = 294,2 г/моль.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HBrO3 + H2S ® HBr + H2SO4

Записать уравнение Нернста для редокс-пары восстановителя.

2. Будет ли перманганат калия окислять ионы SO4 2– до персульфата в кислой среде? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы, если раствор SnCl2 а) недотитрован на 0,2%, б) оттитрован на 100%, в) перетитрован на 0,2%; титрант – дихромат калия 3, [H+] = 1 моль/л?

4. Какую навеску H2C2O4·2H2O следует взять для стандартизации

0,01 М раствора KMnO4 методом а) отдельных навесок б) методом пипетирования (имеется мерная колба объемом 100,0 мл, мерная пипетка вместимостью 10,00 мл), чтобы на титрование расходовалось 15,00 мл раствора KMnO4?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

Na2C2O4 +KMnO4 +H2SO4 ® MnSO4 + Na2SO4 + K2SO4 + H2O + CO2

Записать уравнение Нернста для редокс-пары восстановителя.

2. Будут ли окисляться ионы Сe 3+ под действием бромата калия KBrO3 в кислой среде? Вычислить константу равновесия реакции.

3. Рассчитать скачок на кривой титрования 10,0 мл 0,05 н раствора Ti2(SO4)3 0,05 н раствором K2Cr2O7, если принять погрешность титрования, равной ±0,1%, реакция проводится в сернокислой среде.

4. Каково содержание хлора в литре хлорной воды, если к 25,0 мл хлорной воды прибавили избыток раствора KJ и на титрование выделившегося J2 израсходовали 20,0 мл 0,1 н раствора Na2S2O3?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HNO3 + Cu® NO2 +Cu(NO3)2 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Определить направление, оценить полноту протекания реакции, вычислить константу равновесия реакции:

MnSO4 + Na2SO4+ K2SO4 + H2O → Na2SO3 + KMnO4 + H2SO4

3. Для определения концентрации раствора щавелевой кислоты 10,0 мл его разбавили до 50,0 мл, отобрали 10,0 мл разбавленного раствора и оттитровали 0,1 н раствором перманганата калия. На титрование израсходовано 9,6 мл титранта. Вычислить молярную концентрацию эквивалента щавелевой кислоты.

4. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора Na3AsO3 0,05 н раствором J2, если принять погрешность титрования, равной ±0,1%, а реакция проводится при рН = 0?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

H2O2 + K2SO3 ® K2SO4 +H2O

Записать уравнение Нернста для окислителя.

2. Будут ли в кислой среде окисляться дихроматом калия ионы NO2–? Вычислить константу равновесия реакции.

3.На титрование 0,0630 г щавелевой кислоты в кислой среде затрачено 20,0 мл раствора перманганата калия. Чему равна молярная концентрация эквивалента и титр раствора перманганата калия?

4. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора Na2SO3 0,05 н раствором KMnO4, если принять погрешность титрования, равной ±0,1%, а реакция проводится в сернокислой среде

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KMnO4 + K2SO3 + H2SO4 ® K2SO4 + MnSO4 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора NaNO2 0,1 н раствором KMnO4, если принять погрешность титрования, равной ±0,1%, а реакция проводится при рН = 0?

оттитрованной на 40%, если исходные концентрации веществ одинаковы, титрантом служит KMnO4, [H+] = 1 моль/л?

3. Вычислить константу равновесия, определить полноту протекания и направление реакции:

SnCl4 + KCL + CrCl3 + H2O ® SnCl2 + K2Cr2O7 + HCl

4. Рассчитать массу Mn2+ в растворе, если на его титрование в слабощелочной среде до MnO2 затрачено 21,0мл 0,1н раствора перманганата калия:

Mn 2+ + MnO4 – + ОH– → MnO2↓ + H2O

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

H2S + K2Cr2O7 + H2SO4 ® S + Cr2(SO4)3 + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Вычислить константу равновесия и определить полноту протекания направление реакции:

Cr2(SO4)3 + Ti(SO4)2 + H2O ® K2Cr2O7 + Ti2(SO4)3 + H2O

3. Рассчитать скачок на кривой титрования 10,0 мл 0,2 н Fe2+ 0,2 н раствором дихромата калия при рН = 0. Погрешность 0,2 %.

4. Вычислить массовую долю (%) серы в стали, если сера из навески образца в 3,1640 г после соответствующей обработки превращена в H2S, который окислили 5,0 мл 0,0352 н раствора J2, а избыток последнего оттитровали 3,84 мл 0,05 н раствора Na2S2O3.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KClO3 + S ® KCl + SO2

Записать уравнение Нернста для редокс-пары окислителя.

2. Можно ли действием Се 2+ — ионов восстановить дихромат калия в кислой среде до Cr 3+? Вычислите константу равновесия реакции.

3. Рассчитать скачок на кривой титрования 50,0 мл 0,1 н раствора соли Мора 0,1н раствором бромата калия (погрешность определения составляет ±0,1 %),рН = 0.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KNO2 + KI + H2SO4 ® I2 + NO + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Можно ли действием S 2– — ионов восстановить дихромат калия в кислой среде до Cr 3+? Вычислите константу равновесия реакции.

3. Для случая титрования 10,0 мл 0,1н раствора NaAsO2 раствором 0,1 н KMnO4 при концентрации [Н+]=1 моль/л рассчитать скачок на кривой титрования с допустимой погрешностью 0,1%.

4. Рассчитать %-ное содержание Fe2+ в руде, если на титрование 10,0 мл раствора, полученного после соответствующей химической обработки и разведения в колбе на 200,0 мл, израсходовано 7,4 мл 0,05н перманганата калия. Масса навески руды составляет 0,8000г.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

NaBr + KMnO4 + H2O ® Br2 + MnO2¯ + NaOH + KOH

Записать уравнение Нернста для редокс-пары окислителя.

2. Для случая титрования 20,0 мл 0,1н Fe2+ раствором 0,1н КМnO4 при рН = 0 рассчитайте скачок с допустимой погрешностью определения 0,1%.

3. Рассчитать константу равновесия следующей реакции, оценить полноту протекания и направление реакции:

HBrO3 + H2S ® HBr + H2SO4

4. К 25,0 мл бромной воды прибавили избыток раствора КI, на титрование выделившегося иода израсходовано 15,0 мл 0,1н раствора тиосульфата натрия. Каково содержание Br2 в 200,0 мл бромной воды?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HBr + H2SO4 ® Br2 + H2S + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Можно ли действием нитрита натрия в кислой среде восстановить:

KMnO4 до Mn2+? Вычислите константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы:

SnCl2 + K2Cr2O7 + HCl ® CrCl3 + SnCl4 + KCl + H2O,

когда раствор а) недотитрован на 0,2%, б) оттитрован на 100%, в) перетитрован на 0,2% , если концентрации исходных реагирующих веществ равны. Титрант – дихромат калия, [Н+] = 1 моль/л.

4. Рассчитать титр раствора КМnO4, если на титрование в сернокислой среде навески FeSO4 массой 0,0100г, содержащей 0,1% индифферентных примесей, израсходовано 14,5 мл КМnO4.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HNO3 + P + H2O ® H3PO4 + NO

Записать уравнение Нернста для редокс-пары окислителя.

2. Для случая титрования 20,0 мл 0,1н Na2SO3 раствором 0,1н КМnO4 при рН = 0 рассчитать скачок с допустимой погрешностью определения 0,1%.

3. Навеску щавелевой кислоты массой m = 0,3420 г растворили в мерной колбе на 100мл. На титрование аликвоты в 10,0 мл израсходовано 15,1 мл 0,035 н KMnO4. Чему равна массовая доля Н2О в щавелевой кислоте?

4.Будут ли ионы Br-– окисляться под действием KMnO4. в кислой среде? Вычислите константу равновесия реакции.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

H2SO3 + I2 + H2O ® HI + H2SO4

Записать уравнение Нернста для редокс-пары восстановителя.

2. Для случая титрования 20,0 мл 0,1н НAsO2 раствором 0,1н КBrO3 при [Н+]=0,1 моль/л. рассчитать скачок с допустимой погрешностью определения 0,1%.

3. Чему равен титр раствора KMnO4 по FeSO4, если на титрование 10,0 мл 0,1н раствора FeSO4 в сернокислой среде расходуется 9,0 мл раствора KMnO4 ?

4. Вычислить константу равновесия, определить полноту протекания и направление реакции:

Mn2+ + NO3– + H2O ® MnO4– + HNO2 + H+

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

K2Cr2O7 + KI + H2SO4 ® Cr2(SO4)3 +I2 + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Вычислить константу равновесия реакции. Определить направление и полноту протекания реакции:

KMnO4 + NaBr + H2O ® Br2 + MnO2¯ + NaOH + KOH

3.Для случая титрования 20,0 мл 0,1н NaNO2 раствором 0,1н КМnO4 при рН = 0 рассчитать скачок с допустимой погрешностью определения 0,1%.

4. Чему равен титр раствора KMnO4 по H2O2, если на титрование 10,0мл 0,1н раствора перекиси водорода расходуется 6,0 мл KMnO4?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KBrO3 + SbCl3 + HCl ® KBr + SbCl5 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Вычислить окислительно-восстановительный потенциал системы:

НAsO2 + КBrO3 + H2O ® Н3AsO4 + КBr

когда раствор а) недотитрован на 0,2%, б) оттитрован на 100%, в) перетитрован на 0,2 %; концентрации исходных реагирующих веществ равны. Титрантом является раствор бромата калия, [Н+] = 0,1 моль/л.

3. Можно ли действием SO32– — ионов восстановить дихромат-ионы до Сr3+? Вычислите константу равновесия реакции.

4. Вычислить содержание Fe2O3 (г) в навеске руды, если на титрование полученного из навески раствора Fe2+ израсходовано 20,0 мл раствора K2Cr2O7. Т(K2Cr2O7/Fe2O3 ) = 0,0075 г/мл; М(Fe2O3 ) = 159,7 г/моль

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

K2MnO4 + H2O ® KMnO4 + MnO2¯ + KOH

Записать уравнение Нернста для редокс-пары окислителя.

2. Вычислить окислительно-восстановительный потенциал системы:

НAsO2 + КBrO3 + H2O ® Н3AsO4 + КBr

3. Будут ли ионы Сr3+ окисляться перманганатом калия в кислой среде? Вычислите константу равновесия реакции.

4. Какую навеску H2C2O4 2H2O следует взять для стандартизации

0,01М KMnO4 методом: а) методом отдельных навесок; б) методом пипетирования (Vк = 100,0мл; Vа = 10,0мл), чтобы на титрование в обоих случаях расходовалось бы 10,0 мл перманганата калия?

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HClO4 + K2SO3 ® HCl + K2SO4

Записать уравнение Нернста для редокс-пары окислителя.

2. Вычислить константу равновесия реакции. Определить направление и полноту протекания реакции:

Cr2O3 + KNO3 + KOH ® K2CrO4 +KNO2 + H2O

3. Рассчитать массу MnO4– в растворе, если на титрование 10,0 мл KMnO4 из мерной колбы вместимостью 100,0мл израсходовано 5,0 мл 0,1000 н раствора Fe2+ в сернокислой среде.

4. Рассчитать скачок на кривой титрования 10,0 мл 0,01н раствора Fe2+ 0,02н раствором K2Cr2O7 с погрешностью 0,1%, рН=0.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

MnO2 + H2C2O4 + H2SO4 ® MnSO4 + 2CO2 + 2H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Вычислить константу равновесия реакции. Определить направление и полноту протекания реакции:

NaJ + Na2S4O6 ® Na2S2O3 + J2

3. Для определения концентрации раствора щавелевой кислоты 20,0 мл его разбавили до 100,0мл, отобрали 10,0 мл и оттитровали 8,0 мл 0,05н раствора KMnO4. Чему равен титр исходного раствора щавелевой кислоты?

4. Рассчитать скачок на кривой титрования 10,0 мл 0,1 н раствора соли Мора 0,05н раствором дихромата калия, рН = 0; (погрешность определения 0,1 %).

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

K2Cr2O7 + KI + H2SO4 ® Cr2(SO4)3 +I2 + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Будут ли в кислой среде окисляться броматом калия ионы Сu+? Вычислите константу равновесия реакции.

3. Для случая титрования 20,0 мл 0,1н SnCl2 раствором 0,1н K2Cr2O7 при рН = 0 рассчитать скачок с допустимой погрешностью определения 0,1%.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KMnO4 + H2O2 + H2SO4 ® MnSO4 + K2SO4 + O2 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Для случая титрования 20,0 мл 0,1н NaNO2 раствором 0,1н KMnO4 при рН = 0 рассчитать скачок с допустимой погрешностью определения 0,1%.

3. Каково содержание хлора в литре хлорной воды, если к 25,0 мл хлорной воды прибавили KJ и на титрование выделившегося J2 израсходовали 20,0 мл 0,1 н раствора Na2S2O3?

4. Вычислить константу равновесия, определить полноту протекания и направление реакции:

SnCl2 + K2Cr2O7 + HCl ® SnCl4 + KCL + CrCl3 + H2O

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

KNO2 + KI + H2SO4 ® I2 + NO + K2SO4 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Будут ли окисляться ионы AsO2 – под действием бромата калия KBrO3 в кислой среде? Вычислите константу равновесия реакции.

3. Для случая титрования 20,0 мл 0,1н Na2SO3 раствором 0,1н KMnO4 при рН = 0 рассчитать скачок с допустимой погрешностью определения 0,1%.

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

CrCl3 + (NH4)2S2O8 + H2O ® (NH4)2Cr2O7 + NH4Cl + H2SO4 + HCl

Записать уравнение Нернста для редокс-пары восстановителя.

2. Вычислить окислительно-восстановительный потенциал системы, а) недотитрованной на 0,1%, б) оттитрованной на 100%, в) перетитрованной на 0,1%, титрант – KBrO3, [H+] = 1 моль/л.

SnCl2 + KBrO3 + HCl ® SnCl4 + KBr + H2O

3. Можно ли действием S 2– — ионов восстановить дихромат калия в кислой среде до Cr 3+? Вычислите константу равновесия реакции.

Mn 2+ + MnO4 – + ОН – ® MnO2 + H2O

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

HNO3 + Cu ® NO + Cu(NO3)2 + H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Для случая титрования 20,0 мл 0,1н Ti2(SO4)3 раствором 0,1н K2Cr2O7 при рН = 0 рассчитать скачок с допустимой погрешностью определения 0,1%.

3. Можно ли действием ионов Ce 2+ восстановить перманганат-ионы до Mn 2+ в кислой среде? Вычислите константу равновесия реакции

4. Рассчитать массу навески руды, содержащей около 60% Fe2O3, чтобы на титрование Fe 2+ , полученного при ее обработке, расходовалось бы 12,45 мл 0,1 н раствора KMnO4 .

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

J2 + Na2S2O3 ® NaJ + Na2S4O6

Записать уравнение Нернста для редокс-пары восстановителя.

2. Можно ли действием KMnO4 в нейтральной среде окислить NO2–ионы? Вычислить константу равновесия реакции.

3. Вычислить окислительно-восстановительный потенциал системы

Ti2(SO4)3 + KBrO3 + 3H2SO4 ® Ti(SO4)2 + KBr + H2O,

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

H2S + HNO3 ® H2SO4 + NO2 + H2O

Записать уравнение Нернста для редокс-пары восстановителя.

2. Будет ли перманганат калия окислять ионы Ce 3+в кислой среде? Вычислить константу равновесия реакции.

4. Для установки титра

1. Определить фактор эквивалентности и молярную массу эквивалента реагирующих веществ, уравнять:

H2O2 + K2SO3 ® K2SO4 +H2O

Записать уравнение Нернста для редокс-пары окислителя.

2. Будут ли в кислой среде окисляться дихроматом калия ионы NO2–? Вычислить константу равновесия реакции.

Расчеты в методе редоксиметрии.

Методические указания и варианты контрольных заданий

к самостоятельной работе по дисциплине

«Аналитическая химия и ФХМА»для студентов II курса ХТФ

направления 240100– «Химическая технология и биотехнология»

кандидат хим. наук,

Подписано к печати . .2009. Формат 60х84/16. Бумага «Классика».

Печать RISO. Усл. печ. л. . Уч.-изд. л. .

Заказ. Тираж 100 экз. Цена свободная.

Томский политехнический университет

Система менеджмента качества

Томского политехнического университета сертифицирована

NATIONAL QUALITY ASSURANCE по стандарту ISO 9001:2000

. г. Томск, пр. Ленина, 30.

Видео:РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:

Получается, что потенциал KMnO₄ стал меньше, чем у хлора, а значит, реакция не пойдет.

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Окислительно-восстановительные процессы в анализе

Окислительно-восстановительные реакции (ОВР) в растворах широко используют в анализе. На проведении ОВР основаны:

· разложение анализируемых материалов (растворение сплавов в азотной кислоте и т. п.);

· предварительное окисление или восстановление определяемого вещества;

· маскирование мешающих компонентов путем их перевода в другую степень окисления;

· некоторые реакции обнаружения в качественном анализе;

· редоксметрические методы (перманганатометрия, иодометрия, хроматометрия и др.);

· многие электрохимические методы анализа (вольтамперометрия, кулонометрия, электрогравиметрия, разделение смесей путем электролиза при контролируемом потенциале).

Полуреакции и их потенциалы. Уравнение Нернста. Напомним, что окислительно-восстановительные реакции – это реакции переноса электронов. Любая ОВР может быть представлена суммой двух полуреакций. Общий вид любой полуреакции[1]:

Первая полуреакция описывает присоединение электронов (восстановление) при переходе окислителя Ох₁ в его восстановленную форму Red₁, вторая – отдачу электронов (окисление) при переходе восстановителя Red₂ в его окисленную форму Ох₂. Суммируют полуреакции, уравнивая число отданных и принятых электронов.

Ох₁ + z₁e ÆRed₁ Red₂ ÆОх₂ + z₂e

z₂ z₁

Переходящие друг в друга окисленная и восстановленная частицы рассматриваются как две формы одного и того же вещества, составляющие редокс-пару. Для ОВР обязательно нужны две редокс-пары, различающиеся по своим характеристикам.

Окислительно-восстановительная реакция может протекать в растворе – при непосредственном столкновении частиц Ох₁ и Red₂ или в ходе сложного многостадийного процесса. Кроме того, полуреакции можно пространственно разделить, провести восстановление Ох₁ на одном электроде (катоде), а окисление Red₂ – на другом электроде (аноде). Такая возможность является специфической особенностью ОВР и отличает их, например, от кислотно-основных реакций, где пространственно разделить отдачу и присоединение протонов нельзя.

Независимо от того, каким способом проводится окислительно-восстановительный процесс – прямо в растворе или на электродах, равновесие между обеими формами редокс-пары и соответствующую полуреакцию характеризует окислительно-восстановитель-
ный потенциал (редокс-потенциал). Чем больше этот потенциал (E), тем больше сила окислителя из данной пары, его способность окислять другие вещества. И наоборот, чем меньше редокс-потенциал полуреакции, тем больше сила восстановителя[2].

Рис. 3.8. Сила окислителей и восстановителей в водном растворе
в зависимости от стандартного потенциала редокс-пар

Примером могут быть редокс-пары Fe 3+ / Fe 2+ (Е 0 = 0,771 В) и I₂ / 2I – (Е 0 = 0,545 В). Как известно из курса общей химии, окислитель из пары с более высоким потенциалом может окислить восстановитель из любой пары с меньшим потенциалом. В частности, ионы Fe 3+ могут окислить иодид-ионы до молекулярного иода, но иод не может окислить ионы Fe 2+ .

Таким образом, потенциал полуреакции – очень важная характеристика, и в справочной литературе можно найти значения таких потенциалов для разных редокс-пар. Естественно, все значения Е приводятся там для одних и тех же стандартных условий, в этом случае они обозначаются символом Е 0 . Значения Е 0 можно вычислить по изменению энтальпии и энтропии данной системы, но обычно для измерений используют электрохимический метод. А именно, потенциал полуреакции считают равным равновесному потенциалу индикаторного платинового электрода, опущенного в раствор, содержащий одновременно и окисленную, и восстановленную форму.

Непосредственно измерить потенциал отдельного электрода невозможно, но можно измерить разность потенциалов двух электродов, т. е. электродвижущую силу (э.д.с.) гальванического элемента, состоящего из индикаторного электрода и электрода сравнения, обладающего постоянным потенциалом. В качестве электрода сравнения при таких измерениях используют стандартный водородный электрод (СВЭ) из платины, покрытой слоем платиновой черни; электрод погружен в раствор соляной кислоты с 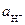=1 и омывается потоком газообразного водорода при давлении 1 атм. Потенциал этого электрода, т. е. потенциал полуреакции 2Н + + 2e – ÆН_{2 (газ)}, условно принят за 0. На практике в качестве электрода сравнения обычно используют не СВЭ, а другие, более простые по конструкции и более удобные в работе электроды (хлоридсеребряный или насыщенный каломельный), потенциалы которых относительно СВЭ точно известны.

Таким образом, потенциал индикаторного электрода равен э.д.с. гальванического элемента, включающего этот электрод и стандартный водородный электрод. Если при замыкании гальванического элемента на индикаторном электроде самопроизвольно происходит восстановление окисленной формы (на водородном электроде при этом идет процесс окисления), то потенциалу исследуемой полуреакции приписывают знак «+» и наоборот.

Потенциал полуреакции связан с изменением энергии Гиббса:

где z – числоэлектронов; F = 96486 Кл/моль – постоянная Фарадея. Зависимость (3.59) позволила немецкому физико-химику Вальтеру Нернсту вывести уравнение, связывающее потенциал полуреакции с активностями (а следовательно, и с концентрациями) окисленной и восстановленной форм данной окислительно-восстановительной пары. Уравнение Нернста записывают в следующем виде:

Е = Е 0 + , (3.60)

где R – универсальная газовая постоянная (8,314 Дж∙моль –1 ∙К –1 ),
Т – температура (в кельвинах), Е 0 – стандартный потенциал полуреакции, который измеряется в стандартных условиях (T = 298 K (25 ºС), p = 1 атм, a_Ox = a_Red = 1) и выражается в вольтах. Преобразуя натуральные логарифмы в десятичные и подставляя значения R, F и T = 298 K, получаем уравнение Нернста в следующей форме:

Е = Е 0 + lg . (3.61)

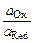
Так, для полуреакции

Fe 3+ + е ÆFe 2+ Е = 0,771 + 0,0591 lg .

В уравнение Нернста, как и в выражения констант равновесия, не включают равные единице активности веществ в стандартном состоянии, в том числе твердых веществ и молекул растворителя. Если в записи полуреакции перед символом какой-либо частицы стоит отличный от единицы стехиометрический коэффициент, то активность частицы в уравнение Нернста входит в степени, равной стехиометрическому коэффициенту. В условиях, когда влиянием ионной силы можно пренебречь и считать все коэффициенты активности равными единице, вместо активностей в уравнение Нернста подставляют равновесные концентрации соответствующих частиц.

Например, для полуреакции

O₂ + 4 H + + 4 e Æ2 H₂O E = 1,23 + lg [O₂] [H + ] 4 .

В данном случае символом [O₂] характеризуют концентрацию растворенного в воде кислорода, и ее связь с потенциалом электрода позволяет потенциометрическим методом контролировать содержание кислорода в воде водоемов.

Отметим, что уравнение Нернста, как и другие закономерности химической термодинамики, не учитывает кинетику окислительно-восстановительных превращений. Измеренные в эксперименте электродные потенциалы могут не совпадать с рассчитанными по уравнению Нернста значениями Е, если в соответствующих полуреакциях равновесие устанавливается медленно. К невыполнению уравнения Нернста приводят также термодинамическая необратимость соответствующих полуреакций и возникновение смешанных потенциалов. Термодинамически обратимы обычно системы, в которых происходит только перенос электронов, без перестройки химических связей в молекулах или ионах. Например, редокс-пара Fe 3+ / Fe 2+ обратима, в отличие от необратимой редокс-пары Cr₂O₇ 2– , Н + / Cr 3+ , Н₂О.

Смешанные потенциалы возникают в системах, в которых превращение форм сопровождается переносом более чем одного электрона. Механизм такого процесса часто сложный, состоящий из ряда одноэлектронных стадий. В результате этого в растворе одновременно присутствует несколько редокс-пар, и экспериментально измеряется обусловленный ими смешанный потенциал, не совпадающий с теоретически предсказанным по уравнению Нернста. Например, полуреакция

MnO₄ – + 8 H + + 5 e – Æ Mn 2+ + 4 H₂O

идет по многоступенчатому механизму. Процесс сопровождается возникновением редокс-пар MnO₄ – /MnO₄ 2– , Mn 3+ /Mn 2+ и др. В результате измеряемый потенциал оказывается смешанным, он значительно ниже теоретического.

Константа равновесия ОВР.В отличие от других типов реакций в растворах, константы равновесия окислительно-восстанови-
тельных реакций не приводятся в справочниках, их рассчитывают по величинам стандартных потенциалов соответствующих полуреакций.

Запишем выражение концентрационной константы равновесия для некоторой реакции:

К = . (3.62)

Пренебрегая влиянием ионной силы, выпишем уравнения Нернста для полуреакций:

Е₁= + lg ; Е₂= + lg .

В условиях равновесия потенциалы обеих полуреакций равны:

+ lg = + lg .

Приведем это уравнение к общему знаменателю (умножим на z₁z₂) и сгруппируем слагаемые:

= z₁lg – z₂ lg = lg .

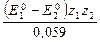
Легко заметить, что в полученном выражении под знаком логарифма находится константа равновесия ОВР, выраженная в (3.62) через равновесные концентрации реагентов. Следовательно, получена искомая формула, связывающая константу равновесия со стандартными потенциалами полуреакций:

lgК = . (3.63)

В полученном равенстве величина z – общее число электронов, передаваемых в ОВР по вышеприведенному уравнению (произведение z₁ и z₂, или их наименьшее общее кратное). Например, при z₁ = 3 и z₂ = 1 z = 3; при z₁ = 2 и z₂ = 6 z = 6. Знак логарифма константы равновесия определяется знаком разности . Первой полуреакцией считают ту, которая представлена в левой части уравнения ОВР своей окисленной формой. Из (3.63) следует, что при lgК > 0, К > 1, т. е. равновесие смещено вправо, реакция идет в заданном направлении. Напротив, при lgК 2– + 6 I – + 14 H + Æ2 Cr 3+ + 3 I₂ + 7 H₂O

Cr₂O₇ 2– + 14 H + + 6 е Æ2 Cr 3+ + 7 H₂O = 1,33 В

2 I – – 2 е ÆI₂ = 0,54 В

В левой части уравнения ОВР окислителем является дихромат, следовательно, стандартный потенциал полуреакции с участием дихромата обозначен символом правильно. Теперь подставляем стандартные потенциалы полуреакций в формулу (3.63).

lgК = = = 80,3 К = 10 80,3

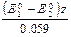
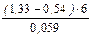
Громадное значение константы равновесия говорит о том, что равновесие ОВР смещено в сторону образования продуктов, реакция проходит количественно. Следовательно, иодиды окислять дихроматом в кислой среде можно.

Оценивая возможность проведения ОВР с помощью формулы (3.63), следует помнить о двух важных ограничениях:

· формула (3.63) применима для оценки состояния равновесия только в стандартных условиях, в частности, в отсутствие посторонних веществ, вступающих в побочные реакции с окислителем и восстановителем, а также с продуктами ОВР. Если же условия отличаются от стандартных и ОВР осложнена побочными процессами (протолиз, комплексообразование и т. п.), то в уравнение (3.63) вместо стандартных потенциалов и следует подставлять формальные потенциалы и рассчитывать условную константу равновесия ОВР. Этот вопрос рассмотрен в следующем подразделе;

· многие ОВР не удается применить в анализе даже тогда, когда lg K усл >> 1. Это обычно связано с замедленностью достижения равновесия или с одновременным протеканием нескольких реакций, т. е. образованием смеси продуктов.

Факторы, влияющие на силу окислителей и восстановителей.В условиях, отличных от стандартных, окислительно-восстано-
вительные свойства веществ характеризуют с помощью формальных потенциалов (Е 0‘ ). Так называют электродный потенциал платинового электрода, опущенного в раствор, где концентрации окисленной и восстановленной форм исследуемого вещества равны 1 моль/л, а концентрации всех других компонентов точно известны. Те же потенциалы иногда называют «кажущимися», реальными или реальными стандартными потенциалами. Последний термин наиболее точен по сути – формальный потенциал аналогичен стандартному, но измеряется не в стандартных, а в реальных условиях, в частности, в присутствии посторонних веществ. Как и стандартные потенциалы, формальные потенциалы измеряют относительно водородного электрода и выражают в вольтах. В отсутствие побочных процессов при нулевой ионной силе и 298 К формальный потенциал совпадает со стандартным потенциалом той же полуреакции: Е 0‘ = Е 0 . Однако при добавлении в исследуемый раствор посторонних веществ, реагирующих с одним из участников данной полуреакции, а также при изменении рН или ионной силы измеренное значение Е 0‘ начинает отличаться от Е 0 (рис. 3.9).

Рис. 3.9. Влияние некоторых посторонних веществ (Y)
на формальный потенциал редокс-пары Fe(III) / Fe(II) в кислой среде:
1 – NaClO₄; 2 – Na₃PO₄; 3 – NaF; 4 – o-фенантролин

Величину Е 0‘ для любых заданных условий можно заранее вычислить, если известна константа равновесия побочной реакции или состояние вещества в растворе (мольная доля реакционноспособной формы). Такие вычисления фактически сводятся к внесению поправок к стандартным потенциалам. Рассмотрим некоторые частные случаи.

1. Поправка на ионную силу раствора (например, из-за присутствия в растворе постороннего электролита с известной высокой концентрацией). Ее можно найти, если записать уравнение Нернста и выделить влияние коэффициентов активности в виде отдельного слагаемого. А именно:

Е = Е 0 + lg = Е 0 + lg =

= Е 0 + lg + lg .

Если концентрации окисленной и восстановленной форм равны, третье слагаемое будет равно нулю. Измеренный в таких условиях потенциал полуреакции – это формальный потенциал. Следовательно,

Е 0‘ = Е 0 + lg . (3.64)

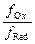
Величина Е 0‘ зависит от соотношения коэффициентов активности окисленной и восстановленной форм. Различие между величинами Е 0‘ и Е 0 обычно невелико, особенно при низкой ионной силе. Так, инертный электролит NaClO₄ почти не влияет на формальный потенциал полуреакции Fe 3+ + e – ÆFe 2+ (кривая 1 на рис. 3.9 практически горизонтальна). Стандартный потенциал этой полуреакции равен 0,771 В, а формальный потенциал при I = 0,1 равен 0,75 В. На практике влиянием ионной силы пренебрегают, считая, что Е 0‘ ≈ Е 0 .

2. Поправка на величину рН раствора. Изменение рН влияет лишь на те полуреакции, в которых участвуют ионы водорода или гидроксила. В практике анализа часто используют редокс-системы, в которых окисленной формой является кислородсодержащая частица, и ее восстановление происходит с участием ионов водорода (например, перманганат-, дихромат-, бромат-ион). Такие полуреакции можно записать в обобщенной форме:

Ox + mH + + ze – ÆRed + 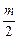H₂O.

Запишем уравнение Нернста для полуреакций данного типа и преобразуем его:

Если [Ox] = [Red], третье слагаемое обращается в 0. Но потенциал, измеренный при равенстве концентраций окисленной и восстановленной форм – это формальный потенциал Е 0‘ .

Е 0‘ = Е 0 + lg[H + ] = Е 0 – рН. (3.65)

Значение рН = 0 отвечает стандартным условиям, в этом случае Е 0‘ =Е 0 . При повышении рН величина Е 0‘ уменьшается, т. е. окислитель рассматриваемого типа становится слабее.

Пример 3.20. Рассчитать формальный потенциал восстановления перманганат-иона в кислой среде. Расчет провести для значений рН 1,0; 2,0 и 3,0.

Решение. Запишем полуреакцию:

MnO₄ – + 8H + + 5e – ÆMn 2+ + 4H₂O.

Находим в справочной литературе величину стандартного потенциала. Е 0 = 1,51 В. Поправку вносим по формуле (3.65). В данном случае z = 5, m = 8. Для раствора с рН = 1 получаем:

Е 0‘ =Е 0 – рН = 1,51 – = 1,42 В.

Расчет при рН = 2 дает Е 0‘ = 1,32 В; при рН = 3 Е 0‘ = 1,23 В. Очевидно, с ростом рН сила перманганата как окислителя уменьшается. Так, при рН = 2–3, в отличие от более кислых растворов, перманганат не способен окислять хлориды, поскольку полуреакция окисления хлор-иона до молекулярного хлора имеет более высокий формальный потенциал (Е 0 ‘ = Е 0 =1,36 В, причем величина рН на формальный потенциал системы Cl₂/2Cl – не влияет).

3. Поправка на процесс комплексообразования. Присутствие в растворе лигандов влияет на те редокс-пары, в составе которых есть катионы металлов, способные реагировать с этими лигандами, образовывать комплексы. Как и в предыдущих случаях, чтобы вывести искомую формулу, надо записать уравнение Нернста, преобразовать его, а затем использовать условие равенства общих концентраций окисленной и восстановленной формы.

Рассмотрим случай, когда и окисленная, и восстановленная формы растворенного вещества могут связываться в комплексные соединения, а электроактивными являются именно несвязанные в комплекс частицы. Тогда из формулы (3.49) следует:

[Ox] = ; [Red] = .

Подставляем полученные выражения в уравнение Нернста в его концентрационной форме.

Е ≈ Е 0 + lg ≈ Е 0 + lg ≈
≈ Е 0 + lg + lg .

Если общие концентрации окисленной и восстановленной форм равны (С_Ox = C_Red ), то, как и в предыдущих случаях, измеренный потенциал является формальным, а третье слагаемое обращается в 0. Получаем:

Е 0‘ = Е 0 + lg . (3.66)

Чем больше закомплексованность окисленной формы, тем ниже формальный потенциал полуреакции, т. е. соответствующий окислитель становится слабее, а восстановитель – сильнее. Именно это показывают кривые 2 и 3 на рис. 3.9: фосфаты и фториды связывают железо(III) в прочные комплексы. Если в побочной реакции комплексообразования участвует восстановленная форма редокс-пары, то по мере увеличения концентрации лиганда окислитель становится сильнее, а восстановитель – слабее. Примером может быть кривая 4 на рис. 3.9, ее вид объясняется тем, что о-фенантролин дает прочные комплексы с ионами железа(II). Наконец, если комплексообразование с данным лигандом присуще и окисленной, и восстановленной форме, то характер изменения Е 0‘ зависит от того, в каком случае образуются более прочные комплексы.

Пример 3.21. Рассчитать формальный потенциал полуреакции
Fe 3+ + e – Æ Fe 2+ в растворе, содержащем избыток цианид-ионов
([CN – ] = 0,1 моль/л).

Решение. В данном случае формальный потенциал отличается от стандартного ввиду одновременного связывания обеих форм железа в цианидные комплексы. Используем формулу (3.66):

Е 0‘ =0,771 + 0,059 lg .

Функции закомплексованности рассчитаем, пользуясь справочными значениями lgb цианидных комплексов железа. Более прочный комплекс дает окисленная форма. Из (3.47) следует:

= 7,9·10 36 ; = 7,9·10 43 ;

Е 0‘ = 0,771 + 0,059 lg10 –7 = 0,357 В .

Формальный потенциал полуреакции стал существенно ниже стандартного, т. е. в присутствии цианидов железо(III) будет более слабым окислителем, а железо(II) – более сильным восстановителем. Этот способ регулировки силы окислителей и восстановителей можно использовать в практике титриметрического анализа, но для снижения потенциала пары Fe 3+ /Fe 2+ лучше брать более безопасные реагенты, например, связывать железо(III) в фосфатные комплексы.

Подобно комплексообразованию, на силу окислителей и восстановителей влияют и реакции осаждения, и другие побочные процессы. Можно дать общую рекомендацию: для увеличения силы окислителя следует связывать в устойчивое соединение (комплекс, осадок) восстановленную форму соответствующей редокс-пары, и наоборот, для увеличения силы восстановителя связывают в устойчивые соединения его окисленную форму.

Пользуясь формальными потенциалами, можно оценить возможность и степень протекания ОВР в любых заданных условиях. Для этого в формулу (3.63) вместо стандартных потенциалов полуреакций подставляют формальные потенциалы, «исправленные» с учетом заданных условий, как в приведенных примерах. Затем рассчитывают константу равновесия (пример 3.22), а затем, в случае необходимости, рассчитывают степень протекания реакции и равновесные концентрации всех реагентов. Для практики важны и задачи другого типа, суть которых – нахождение условий, в которых равновесие некоторой ОВР смещено в желаемую сторону. Такие задачи также решают с помощью формальных потенциалов (пример 3.23).

Пример 3.22. Оценить возможность окисления иодид-ионов мышьяковой кислотой при рН 7.

Решение. Выпишем уравнение реакции и потенциалы полуреакций:

В стандартных условиях константа равновесия составит:

К = = 3,2.

Константа довольно мала, т. е. в стандартных условиях (рН = 0) реакция идет не до конца. Переход к рН = 7 не повлияет на полуреакцию, в которой участвуют иодид-ионы, но скажется на формальном потенциале полуреакции с участием мышьяковой кислоты.

Е 0‘ = Е 0 – 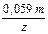рН = 0,56 – = 0,147 В.

К усл = = 3,4·10 –14 .

Очевидно, в нейтральной среде окислить иодиды мышьяковой кислотой нельзя. Равновесие ОВР смещено в обратную сторону – в сторону окисления арсенит-ионов иодом. Последний процесс используют в титриметрическом анализе (иодометрическое титрование арсенитов при рН 7–8).

Пример 3.23. Определить, при каких значениях рН раствора иодиды можно окислять до молекулярного иода, применяя иодат калия в качестве окислителя.

Решение. Выпишем уравнение реакции и потенциалы полуреакций:

2 IO₃ – + 12 H + + 10 е Æ I₂ + 6 H₂O = 1,19 В

I₂ + 2 е Æ 2 I – = 0,54 В.

Будем считать, что равновесие реакции смещено вправо при К_равн > 1 и влево, если К_равн 0‘ = Е₂ 0‘ . Формальный потенциал первой полуреакции является функцией рН, а потенциал второй от рН не зависит. Из (3.65) следует, что

Е 0‘ = Е 0 – 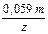рН = 1,19 – = 1,19 – 0,071 рН = 0,54.

Полученному равенству соответствует рН = = 9,1. В более кислой среде (при рН + , E 0 = +1,23 B (при рН = 7 Е 0‘ = +0,815 В).

Водные растворы сильных окислителей, относящихся к редокс-парам с более высокими потенциалами ( > 1,23 В в кислой среде, > 0,815 В в нейтральной среде), термодинамически неустойчивы. Примером могут быть водные растворы перманганата, сульфата кобальта(III), сульфата церия(IV). Выделение кислорода на холоду идет очень медленно, но ускоряется при нагревании раствора.

· Вода может окислять растворенные вещества-восстанови-
тели, выделяя водород.

2 Н₂О + 2e – ÆН₂ + 2 ОН – , E 0 = – 0,828 B (при рН = 0 Е 0‘ = 0 В;
при рН = 7 Е 0‘ = – 0,414 В).

Водные растворы сильных восстановителей, относящихся к редокс-парам с более низкими формальными потенциалами ( + + 4e Æ2 Н₂О, E 0 = +1,23 B (при рН = 7 Е 0‘ = +0,815 В).

Эта полуреакция характеризует не только восстановительные свойства воды (см. выше), но и окислительные свойства растворенного в воде кислорода. Причем кислород – более сильный окислитель, чем вода, он может окислять и те вещества, которые водой не окисляются (например, соли железа(II) или иодиды). Окисляются восстановленные формы всех редокс-пар, где Е 0‘

📺 Видео

ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Продукты в ОВР. Ч.2-2. Окислительно-восстановительный (редокс) потенциал в растворе.Скачать

011 Электрохимия 4 уравнение НернстаСкачать

Лекция 4 Уравнение Нернста. Электрохимическое равновесиеСкачать

ОВР часть 2. Окислительно-восстановительные реакции. Электродный потенциал.Скачать

Окислительно-восстановительные равновесия в аналитической химии.Скачать

Окислительно-восстановительные реакции в щелочноной среде. Упрощенный подход.Скачать

Окислительно-восстановительные реакции. 3 часть. 9 класс.Скачать

Окислительно-восстановительные реакции. 1 часть. 9 класс.Скачать

ОВР часть 2Скачать

ЕГЭ2020. ХИМИЯ. «Теория Льюиса. Механизмы органических реакций. Уравнение Нернста»Скачать

Составление ур-й окислительно-восст. реакций методом ионно-электронного баланса. 1ч. 10 класс.Скачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Химия | Молекулярные и ионные уравненияСкачать

8 класс. ОВР. Окислительно-восстановительные реакции.Скачать

БЕЗ ЭТОГО НЕ СДАТЬ ЕГЭ по Химии — Электронная конфигурация атомаСкачать

Использование таблиц потенциалов и расчет ЭДС реакции. Продукты в ОВР. Ч.5-1.Скачать