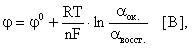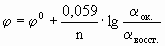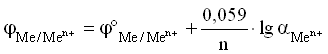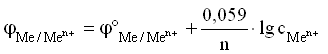Уравнение нернста для медного электрода при 298 к (7 видео)

Лабораторная работа № 5. Исследование электрохимических потенциалов между различными металлами

Лабораторная работа № 5. Исследование электрохимических потенциалов между различными металлами

1. Применение уравнения Нернста

В общем случае для цепи, где число электронов, участвующих в окислительно-восстановительных процессах, протекающих на электродах, различно (z1≠ z2) (–) Ме1 | (a1) || (а2) | Ме2 (+),

уравнение ЭДС будет иметь вид:

Это основное уравнение ЭДС гальванического элемента составленного из двух металлических электродов, его часто называют уравнением Нернста для определения ЭДС гальванического элемента.

ЭДС элемента (Е) рассчитывается как разность величины потенциала катода и величины потенциал анода.

Зависимость электродного потенциала металла от активности потенциалопределяющих ионов в растворе дается уравнением электродного потенциала Нернста:

По данным о стандартных электродных потенциалах меди и цинка рассчитать ЭДС элемента, составленного из полуэлементов:

Решение: Рассчитаем ЭДС по уравнению

Упростим выражение подставив известные величины:

Значение стандартных электродных потенциалов находим в справочнике:

= 0,337 В; = − 0,763 В.

Так как медный полуэлемент более электроположителен, то

Ответ: Е = 1,135 В.

Определить активность ионов меди, если ЭДС цепи

при T = 298 К равна 0,08885 В.

Решение: ЭДС цепи равна разности электродных потенциалов:

откуда x = 0,0013 моль/л.

Ответ: а1 = 0,0013 моль/л.

При Т = 298 К электродный потенциал электрода

равен 0,2712 В. Определить стандартный потенциал медного электрода.

Ответ:

Содержание

Применение уравнения Нернста в решении задач.
Пример 1:
Решение:
Пример 2:
Решение:
Уравнение Нернста. Электродный потенциал любой окислительно-восстановительной системы, находящейся в нестандартных условиях
🎦 Видео

Видео:Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:

Получается, что потенциал KMnO₄ стал меньше, чем у хлора, а значит, реакция не пойдет.

Видео:Уравнение НернстаСкачать

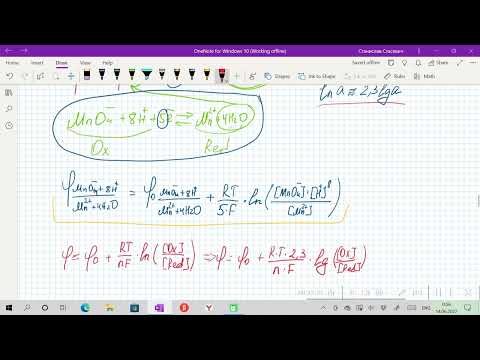
Уравнение Нернста. Электродный потенциал любой окислительно-восстановительной системы, находящейся в нестандартных условиях

Электродный потенциал любой окислительно-восстановительной системы, находящейся в нестандартных условиях, можно рассчитать по уравнению Нернста:

где: φ — электродный потенциал окислительно-восстановительного электрода, В;

φ 0 — стандартный электродный потенциал этого электрода, В, R — универсальная газовая постоянная, равная 8,314 Дж/моль· К, T – температура в K; n — число электронов в уравнении электродной реакции, F — число Фарадея, равное 96500 Кл/моль, a_ок., a _восст. — активности окисленной формы восстановителя (Ме n+ ) и восстановленной формы окислителя (Ме) в электродной реакции. Подставив в уравнение Нернста T = 298 K, R, F и введя множитель 2,3 (переход к десятичным логарифмам), получим:

Уравнение Нернста для металлического электрода имеет вид:

Для разбавленных растворов, в которых активности мало отличаются от концентрации (a » С):

Величина j°_Me n+ _/Me 0 называется стандартным ЭП металлического электрода. Значение ЭП металлического электрода равно величине стандартного ЭП металлического электрода при концентрации ионов металла в растворе, равной 1 моль/л. Стандартный электродный потенциал – равновесная разность потенциалов гальванического элемента, составленного из стандартного водородного электрода (электрод сравнения) и электрода, потенциал которого определяется в стандартных условиях.

Дата добавления: 2015-07-30 ; просмотров: 2579 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ