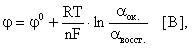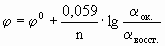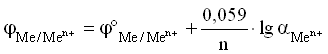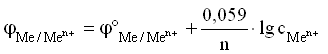Электродный потенциал любой окислительно-восстановительной системы, находящейся в нестандартных условиях, можно рассчитать по уравнению Нернста:
где: φ — электродный потенциал окислительно-восстановительного электрода, В;
φ 0 — стандартный электродный потенциал этого электрода, В, R — универсальная газовая постоянная, равная 8,314 Дж/моль· К, T – температура в K; n — число электронов в уравнении электродной реакции, F — число Фарадея, равное 96500 Кл/моль, aок., a восст. — активности окисленной формы восстановителя (Ме n+ ) и восстановленной формы окислителя (Ме) в электродной реакции. Подставив в уравнение Нернста T = 298 K, R, F и введя множитель 2,3 (переход к десятичным логарифмам), получим:
Уравнение Нернста для металлического электрода имеет вид:
Для разбавленных растворов, в которых активности мало отличаются от концентрации (a » С):
Величина j°Me n+ /Me 0 называется стандартным ЭП металлического электрода. Значение ЭП металлического электрода равно величине стандартного ЭП металлического электрода при концентрации ионов металла в растворе, равной 1 моль/л. Стандартный электродный потенциал – равновесная разность потенциалов гальванического элемента, составленного из стандартного водородного электрода (электрод сравнения) и электрода, потенциал которого определяется в стандартных условиях.
Дата добавления: 2015-07-30 ; просмотров: 2627 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать

Применение уравнения Нернста в решении задач.
При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:
Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:
Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.
Пример 1:
Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO4 и 0.01М ZnSO4 соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.
Решение:
Для начала запишем уравнения протекающих процессов:
Далее находим по таблице стандартные потенциалы процессов:
Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.
Найдем реальные потенциалы с учетом нестандартных активностей ионов:
Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:
Ответ: 1.13 В
Пример 2:
Одним из лабораторных способов получения хлора является действие KMnO4 на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?
Решение:
Для начала запишем уравнения протекающих процессов.
Далее находим по таблице стандартные потенциалы процессов:
Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:
Получается, что потенциал KMnO4 стал меньше, чем у хлора, а значит, реакция не пойдет.
Видео:Урок 298. Электрический ток в жидкостях. Закон Фарадея для электролизаСкачать

ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ И ЭДС
При изучении этого раздела рекомендуется проработать следующие вопросы: понятие об электродных потенциалах; гальванические элементы (ГЭ); электродвижущая сила гальванического элемента (ЭДС) и ее измерение; стандартный водородный электрод и водородная шкала потенциалов; уравнение Нернста; потенциалы металлических, газовых и окислительно-восстановительных электродов; кинетика электродных процессов; электрохимическая и концентрационная поляризация [1, 10].
Гальванический элемент – электрохимическая система, состоящая из электродов, погруженных в раствор электролитов и соединенных между собой металлическим проводником, образующим внешнюю цепь элемента.
В основе работы гальванического элемента лежат процессы, происходящие на границе металлический электрод – электролит, в результате которых образуется двойной электрический слой. За счет двойного электрического слоя возникает скачок потенциала, называемого электродным. Величина электродного потенциала металла является количественной характеристикой его активности. Для того, чтобы можно было сравнивать активность различных металлов вводится понятие стандартного электродного потенциала j о . Чем более отрицательное значение имеет потенциал металла, тем более сильными восстановительными способностями обладает этот металл. И наоборот, чем более положителен потенциал металлического электрода, тем более сильными окислительными способностями обладают ионы.
Величина потенциала металлического электрода зависит от температуры, активности ионов и рассчитывается по уравнению Нернста

где 

R – универсальная газовая постоянная;
Т – абсолютная температура, K;
n – число электронов, участвующих в процессе;
F – постоянная Фарадея, равная 96 548 Кл/моль;

После подстановки значений постоянных и перевода натурального логарифма в десятичный формула Нернста приобретает вид:

Потенциалы водородного и кислородного электродов, являющиеся газовыми электродами, зависят от рН раствора и парциального давления. Потенциалы этих электродов приведены в табл. 10.
Пример 1. Вычислите электродный потенциал водородного электрода в нейтральной среде при 
Решение. Электродный потенциал водородного электрода определяется по уравнению Нернста, исходя из схемы электродного процесса:



Активность ионов водорода в нейтральной среде а 
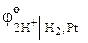
тогда 
Полученное значение 
Пример 2. Серебряный электрод опущен в раствор нитрата серебра AgNO3 с активностью ионов 
Решение. Электродный процесс:


Электродный потенциал серебра рассчитывается по уравнению Нернста:

Пример 3. Составьте схему гальванического элемента, состоящего из железного и медного электродов, опущенных в растворы собственных солей. Напишите ионно-электронные уравнения электродных процессов и вычислите ЭДС этого ГЭ, если активности ионов в соответствующих растворах следующие: 

Решение. Ионно-электронные уравнения электродных процессов:
А: Fe – 2 
K: Cu 2+ + 2 
Железный электрод является анодом, так как его стандартный электродный потенциал ( 

Схема данного в условии гальванического элемента имеет вид:
(–) Fe | Fe 2+ || Cu 2+ | Сu (+)
Определяем ЭДС элемента:
ЭДС
Электродный потенциал анода определяем по уравнению Нернста, а потенциал катода является стандартной величиной:

ЭДС = 0,34 – (– 0,499) = 0,839 В.
Пример 4. Схема гальванического элемента имеет вид:
(–) Zn |ZnCl2 || ZnCl2 |Zn (+). Рассчитайте ЭДС этого элемента, если в одном полуэлементе активность ионов цинка 0,001 моль/л, а в другом – 0,01 моль/л. Напишите уравнения анодного и катодного процессов.
Решение. В условии задачи дан концентрационный гальванический элемент. В таком элементе катодом будет цинк, опущенный в раствор соли с более высокой активностью ионов Zn 2+ = 0,01 моль/л.
Уравнение электродных процессов:
А: Zn – 2 
K: Zn 2+ + 2 
Определяем ЭДС элемента:
ЭДС 
Электродные потенциалы находим по уравнению Нернста:



ЭДС 
Пример 5. Для гальванического элемента:
напишите уравнения электродных процессов и рассчитайте реальную ЭДС с учетом перенапряжения выделения водорода, если активность ионов марганца 1 · 10 –2 моль/л, а ионов водорода 1,0 моль/л (при 
Решение. Уравнения электродных процессов:
А: Mn – 2 
K: 2H + + 2 
При работе гальванического элемента ЭДС и ток уменьшаются. Это связано с изменениями электродных потенциалов анода и катода. Изменение электродных потенциалов, приводящее к уменьшению ЭДС и силы тока, называется поляризацией.
Различают три вида поляризации: газовую, концентрационную и электрохимическую. Разность между равновесным потенциалом электрода и его потенциалом в том же растворе при прохождении электрического тока, называется перенапряжением (табл. 11 приложения).
В условиях данной задачи перенапряжение выделения водорода на катоде 



Электродный потенциал анода определяем по формуле 



ЭДС = – 0,30 – (–1,239) = 0,939 В.
Пример 6. Вычислите величину потенциала окислительно-восстановитель-ного электрода Pt | Sn 4+ , Sn 2+ . Реакция восстановления Sn 4+ + 2 



Решение. Потенциал окислительно-восстановительного электрода определяется по уравнению:

Тогда 
Пример 7. Железный электрод в растворе своей соли имеет электродный потенциал 
Решение. Определяем активность ионов железа, используя уравнение Нернста:
так как 




Пример 8. Вычислите стандартную ЭДС гальванического элемента, в котором установилось равновесие:
Zn + 2Ag + « Zn 2+ + 2Ag ,
если 

Решение. Стандартная ЭДС гальванического элемента определяется по уравнению:
– 
где nF – количество электричества, которое теоретически можно получить при электрохимическом превращении одного моля вещества;
F – постоянная Фарадея (F = 96,548 кДж/В · моль), или F » 96 500 Кл/моль,
n – количество электронов, участвующих в процессе, для нашего ГЭ n = 2;


Так как стандартные энергии Гиббса образования простых веществ цинка и серебра равны нулю, то подставляя числовые значения величин, находим:

КОНТРОЛЬНЫЕ ЗАДАНИЯ
201. Составьте схему, напишите ионно-электронные уравнения электродных процессов и вычислите ЭДС цинко-магниевого гальванического элемента, в котором активность ионов цинка 

202. Для гальванического элемента (–) Cr | Cr 3+ || 2H + | H2, Fe (+)
напишите уравнения электродных процессов и рассчитайте реальную ЭДС с учетом перенапряжения выделения водорода, если активность ионов хрома 


203. Алюминиевая и медная пластины соединены внешним проводником и опущены в раствор серной кислоты. Составьте схему гальванического элемента и напишите ионно-электронные уравнения электродных процессов, протекающих на аноде и на катоде.
204. Вычислите электродный потенциал водородного электрода в кислой среде при при 
Ответ: – 9× 10 –3 В.
205. Составьте схему, напишите ионно-электронные уравнения электродных процессов и вычислите ЭДС железно-ртутного гальванического элемента, в котором активность ионов железа 

206. Составьте схему гальванического элемента, в основе которого лежит химическая реакция, протекающая по уравнению:
Напишите ионно-электронное уравнение электродных процессов и вычислите ЭДС этого элемента, если активность ионов магния 

207. Составьте схему гальванического элемента, в основе которого лежит химическая реакция, протекающая по уравнению:
Напишите ионно-электронное уравнение электродных процессов и вычислите ЭДС этого элемента, если активность ионов цинка 

208. Вычислите величину потенциала окислительно-восстановительного электрода Pt | Fe 3+ , Fe 2+ если 


209. Алюминиевый электрод в растворе соли имеет электродный потенциал 
Ответ: 0,095 моль/л.
210. Какой гальванический элемент называется концентрационным? Составьте схему, напишите ионно-электронные уравнения электродных процессов и вычислите ЭДС гальванического элемента, состоящего из двух медных электродов, опущенных в растворы сульфата меди CuSO4 c активностью ионов меди в первом растворе 

211. Составьте схемы двух гальванических элементов, в одном из которых цинк был бы катодом, а в другом – анодом. Напишите для каждого из этих элементов ионно-электронные уравнения реакций, протекающих на катоде и аноде.
212. При какой активности ионов Mn 2+ (моль/л) потенциал марганцевого электрода будет на 0,018 В меньше его стандартного электродного потенциала?
Ответ: 0,25 моль/л.
213. Потенциал медного электрода в растворе хлорида меди CuCl2 составил 97% от величины его стандартного электродного потенциала. Чему равна активность ионов 
Ответ: 0,46 моль/л.
214. Для гальванического элемента
напишите уравнения электродных процессов и рассчитайте реальную ЭДС с учетом перенапряжения выделения водорода, если активность ионов магния 


215. Вычислите ЭДС гальванического элемента, в котором при 298 K установилось равновесие: Mg + Cd 2+ « Mg 2+ + Cd, если активность ионов магния 

216. Вычислите стандартную ЭДС гальванического элемента, в котором установилось равновесие: Fe + Cu 2+ « Fe 2+ + Cu, если известно, что 

217. Составьте схему, напишите ионно-электронные уравнения электродных процессов и вычислите ЭДС железо-медного гальванического элемента, в котором активность ионов железа 

218. Вычислите ЭДС гальванического элемента, в котором при 298 K установилось равновесие: Cd + Cu 2+ « Cd 2+ + Cu, если активность ионов магния 

219. Вычислите ЭДС гальванического элемента, в котором при 298 K установилось равновесие: 2Na + H2O(г) + 1/2O2 « 2NaOH (к) ,
если 

220. Вычислите величину потенциала окислительно-восстановительного электрода Pt | Co 3+ , Co 2+ с активностями ионов кобальта 


Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Обратимые потенциалы металлов, уравнение Нернста.
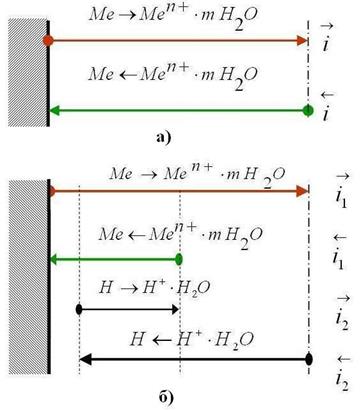
Исходя из предположения, что, если при взаимодействии металла с водным раствором электролита фазовую границу пересекают только ионы металла, то протекают два сопряженных процесса (А. Н. Фрумкин):
1) анодный (окислительный) процесс – переход ионов металла в раствор с образованием гидратированных ионов:
Ме + Н2О = Ме n+ ·mH2O + ne, (4.5) скорость которого, измеряемая числом ионов, переходящих из твердой фазы в жидкую фазу в единицу времени, может быть выражена через плотность соответствующего тока прямого процесса 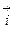
2) катодный (восстановительный) процесс – разряд гидратированных ионов из раствора с выделением их на поверхности металла в виде нейтральных атомов:
Ме n+ ·mH2O + ne = Ме + Н2О, (4.6) скорость обратного процесса определяется соответствующей плотностью тока 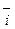
Рис. 4.4. Схема установления электродных потенциалов металлов:
а) – обратимого (равновесного), б) – необратимого.
Какой из этих процессов преобладает, определяется уровнем потенциальной энергии катионов в узлах кристаллической решетки металла ПMe и в растворе Пp. Если ПMe>Пр, то 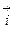
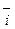
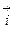
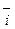
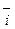
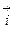
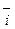
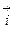
Образующийся ДЭС затрудняет протекание прямого процесса и облегчает протекание обратного. Когда потенциал в нем достигает значения, при котором энергетический уровень ионов в металле и растворе становится одинаковым, ПМе = Пр, устанавливается динамическое равновесие, при котором скорости анодного и катодного процессов равны:
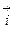
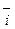
Этому равновесному состоянию соответствует некоторый скачок потенциала металла между металлом и раствором электролита, абсолютная величина которого неизвестна, поскольку разность потенциалов между двумя фазами нельзя измерить непосредственно. Для её определения измеряется э.д.с. элемента, составленного из исследуемого электрода (металла в электролите) и электрода сравнения. Эта э.д.с. и называется электродным потенциалом металла.
Обратимый (равновесный) электродный потенциал металла (ЕMe)o6p или ( 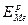
В случае установления обратимого потенциала скорости анодного и катодного процессов равны ( 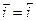
Обратимый (равновесный) электродный потенциал металла рассчитывается по уравнению Нернста, его величина количественно характеризует способность металла посылать свои ионы в раствор электролита.
Уравнение Нернста может получено на основе термодинамических соотношений. Т.к. знак потенциала зависит от направления реакции, обратимо протекающие реакции записываются в восстановительной форме:
Ме n+. mH2O+ ne 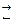
Для этой реакции уравнение изотермы Вант-Гофффа записывается как:
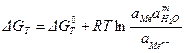
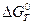
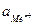
Поскольку, работа по созданию двойного электрического слоя (аналогично соотношению 4.2) равна убыли энергии Гиббса:
де Eдс – потенциал двойного электрического слоя (потенциал гальванического элемента металл-раствор или обратимый потенциал металла Еобр); n – заряд иона металла; F – постоянная Фарадея.
Подставляя (4.9) в уравнение 4.9, поскольку aMe =1, 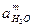
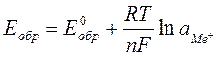
где 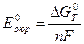
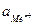
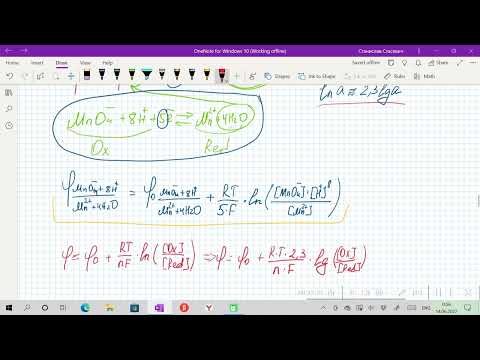
В общем случае, при протекании на поверхности металла, находящегося в контакте с электролитом, окислительно–восстановительной реакции с участием окисленной Ох и восстановленной Red форм вещества:
mOx + ke 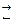
обратимый потенциал этой (катодной) реакции равен:
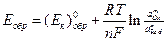
где 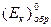
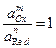
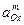
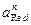
Стандартные потенциалы приведены в таблице 4.1.
Стандартные электродные потенциалы некоторых металлов и
окислительно-восстановительных реакций при 25 0 С.
| Реакция | Потенциал, В | Реакция | Потенциал, В |
| Li + +e=Li | –3,01 | H + + e = ½H2 | 0,000 |
| K + +e=K | –2,925 | Sn 4+ +4e=Sn | 0,007 |
| Na 2+ +2e=Na | –2,900 | Cu 2+ +2e=Cu | 0,337 |
| Mg 2+ +2e=Mg | –2,370 | Cu + +e=Cu | 0,521 |
| Al 3+ +3e=Al | –1,660 | Fe 3+ +e=Fe 2+ | 0,77 |
| Ti 2+ +2e=Ti | –1,630 | Ag + +e=Ag | 0,799 |
| Ti 3+ +3e=Ti | –1,210 | Hg 2+ +2e=Hg | 0,854 |
| Mn 2+ +2e=Mn | –1,180 | Pd 2+ +2e=Pd | 0,987 |
| Cr 2+ +2e=Cr | –0,913 | Ir 3+ +3e=Ir | 1,150 |
| Zn 2+ +2e=Zn | –0,762 | Pt 2+ +2e=Pt | 1,190 |
| Cr 3+ +3e=Cr | –0,740 | Au 3+ +3e=Au | 1,500 |
| Fe 2+ +2e=Fe | –0,440 | Au + +e=Au | 1,690 |
| Cd 2+ +2e=Cd | –0,402 | 2H2O+2e=H2+OH – (щелочные среды) | –0,828 |
| Mn 3+ +3e=Mn | –0,283 | O2+2H2O+4e=4OH – (нейтральные и щелочные среды) | 0,401 |
| Ni 2+ +2e=Ni | –0,250 | 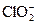 +H2O+2e=ClO – +2OH – (щелочные среды) +H2O+2e=ClO – +2OH – (щелочные среды) | 0,66 |
| Mo 3+ +3e=Mo | –0,200 | NO 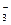 +4H + +3e=NO+2H2O +4H + +3e=NO+2H2O | 0,96 |
| Sn 2+ +2e=Sn | –0,136 | O2+4H + +4e=2H2O (кислоты) | 1,23 |
| Pb 2+ +2e=Pb | –0,126 | Cl2+2e=2Cl – | 1,36 |
| Fe 3+ +3e=Fe | –0,037 | H2O2+2H + +2e=2H2O | 1,78 |
Активность ионов в реакции диссоциации:
определяется как произведение концентрации данного иона на средний коэффициент активности:
где С+, С– – моляльные концентрации соответствующих ионов в растворе, m и n – число катионов и анионов, на которые распадается молекула при диссоциации, f± — средний ионный коэффициент активности.
Для труднорастворимых веществ, например гидрооксидов металлов:
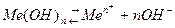
активность ионов металла:
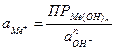
Пример 4.1. Рассчитать обратимый потенциал меди в 0,1 моляльном водном растворе СuSO4 при 298 К (средний ионный коэффициент активности ионов меди в данных условиях, 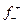
Решение. 1) Окислительно-восстановительная электродная реакция меди: Сu 2+ + 2е 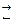
2) Обратимый потенциал меди находим по уравнению Hepнcтa: 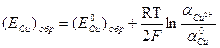
3) Активность ионов меди: 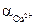
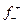
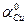
4) Стандартный обратимый потенциал для реакции берем из справочных данных (табл.4.1). Подставляем полученные данные и определяем: 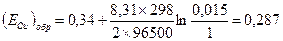
Пример 4.2. Найти обратимый потенциал кислородного электрода в нейтральном 1 m растворе Na2SO4 при 298 К в атмосфере воздуха.
Решение. 1) Кислород восстанавливается в катодном процессе по реакции: 2Н2О+О2+4е=4ОН 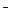
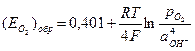
2) Активность газа определяется его парциальным давлением. Парциальное давление кислорода в воздухе 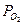
3) Активность гидрооксил-ионов в нейтральном растворе определяется через ионное произведение воды, КВ= 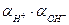
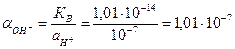
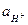
4) Подставляем полученные значения в уравнение Нернста: 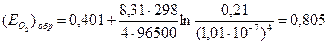
Дата добавления: 2017-02-13 ; просмотров: 3895 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
💡 Видео
Электродные потенциалы металлов. Электроды сравненияСкачать

ОВР часть 2. Окислительно-восстановительные реакции. Электродный потенциал.Скачать

Уравнение Нернста. Условия изменения направления ОВР. Продукты в ОВР. Ч.5-3.Скачать

Продукты в ОВР. Ч.2-1. Электродный потенциал металлов.Скачать

Уравнение НернстаСкачать
Химия 11 класс (Урок№8 - Химические источники тока. Ряд стандартных электродных потенциалов.)Скачать

4 3 Электрохимический потенциалСкачать

Химические уравнения. СЕКРЕТНЫЙ СПОСОБ: Как составлять химические уравнения? Химия 8 классСкачать

011 Электрохимия 4 уравнение НернстаСкачать

В чем отличие ЭДС, Напряжение, Потенциал, Падение НапряженияСкачать

Электродный потенциал, ч 2Скачать

Химия 9 класс — Как определять Степень Окисления?Скачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Химия. Лекция 6. Часть 1. Решение задач на электродные потенциалы и электропроводность растворов.Скачать

Задачи на гальванический элемент. Продукты в ОВР. Ч.5-4.Скачать

Уравнение состояния идеального газа. 10 класс.Скачать