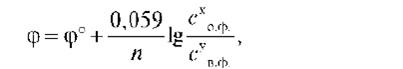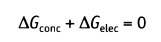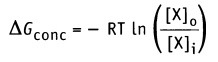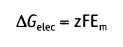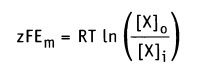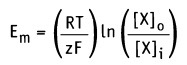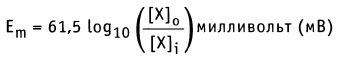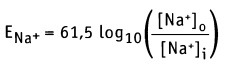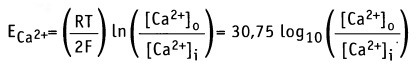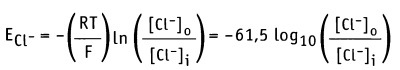Мерой окислительно-восстановительной способности веществ служат окислительно-восстановительные потенциалы. Рассмотрим механизм возникновения потенциала. При погружении химически активного металла (Zn, Al) в раствор его соли, например Zn в раствор ZnSO4, происходят дополнительное растворение металла в результате процесса окисления, образование пары, двойного электрического слоя на поверхности металла и возникновение потенциала пары Zn 2+ /Zn ° .
Металл, погруженный в раствор своей соли, например цинк в растворе сульфата цинка, называют электродом первого рода. Это двухфазный электрод, который заряжается отрицательно. Потенциал образуется в результате реакции окисления (рис. 5.1).
Рис. 5.1. Окисление цинка
При погружении в раствор своей соли малоактивных металлов (Cu) наблюдается противоположный процесс. На границе металла с раствором соли происходит осаждение металла в результате процесса восстановления иона, обладающего высокой акцепторной способностью к электрону, что обусловлено высоким зарядом ядра и малым радиусом иона. Электрод заряжается положительно, в приэлектродном пространстве избыточные анионы соли формируют второй слой, возникает электродный потенциал пары Cu 2+ /Cu ° . Потенциал образуется в результате процесса восстановления (рис. 5.2). Механизм, величина и знак электродного потенциала определяются строением атомов участников электродного процесса.
Рис. 5.2. Восстановление меди
Итак, потенциал, который возникает на границе раздела металла с раствором в результате окислительного и восстановительного процессов, протекающих с участием металла (электрода) и образованием двойного электрического слоя называют электродным потенциалом.
Если отводить электроны с цинковой пластины на медную, то равновесие на пластинках нарушается. Для этого соединим цинковую и медную пластины, погруженные в растворы их солей, металлическим проводником, приэлектродные растворы — электролитным мостиком (трубка с раствором K2SO4), чтобы замкнуть цепь. На цинковом электроде протекает полуреакция окисления: Zn 0 (т) — 2ē → Zn 2+ (р-р), а на медном — полуреакция восстановления: Cu 2+ (р-р) + 2ē → Cu 0 (т)
Электрический ток обусловлен суммарной окислительно-восстановительной реакцией:
Zn 0 (т) + Cu 2+ (р-р) → Zn 2+ (р-р) + Cu 0 (т)
Окислительно-восстановительные потенциалы пары зависят от природы участников электродного процесса и соотношения равновесных концентраций окисленной и восстановленной форм участников электродного процесса в растворе, температуры раствора и описываются уравнением Нернста.
Количественной характеристикой окислительно-восстановительной системы является редокс-потенциал, возникающий на границе раздела фаз платина — водный раствор. Величина потенциала в единицах СИ измеряется в вольтах (В) и рассчитывается по уравнению Нернста-Петерса:
где а(Oх) и a(Red) — активность окисленной и восстановленной форм соответственно; R — универсальная газовая постоянная; Т — термодинамическая температура, К; F — постоянная Фарадея (96500 Кл/моль); n — число электронов, принимающих участие в элементарном редокс-процессе; а — активность ионов гидроксония; m — стехиометрический коэффициент перед ионом водорода в полуреакции. Величина φ° — стандартный редокс-потенциал, т.е. потенциал, измеренный при условиях а(Oх) = a(Red) = a(H + ) = 1 и данной температуре.
Стандартный потенциал системы 2Н + /Н2 принят равным 0 В. Стандартные потенциалы являются справочными величинами, табулируются при температуре 298К. Сильнокислая среда не характерна для биологических систем, поэтому для характеристики процессов, протекающих в живых системах, чаще используют формальный потенциал, определяемый при условии а(Oх) = a(Red), pH 7,4 и температуре 310К (физиологический уровень). При записи потенциала пара указывается в виде дроби, причем окислитель записывается в числителе, а восстановитель в знаменателе.
Для 25°С (298К) после подстановки постоянных величин (R = 8,31 Дж/моль×град; F = 96500 Кл/моль) уравнение Нернста принимает следующий вид:
где φ°- стандартный окислительно-восстановительный потенциал пары, В; Со.ф. и Св.ф. — произведение равновесных концентраций окисленной и восстановленной форм соответственно; х и у — стехиометрические коэффициенты в уравнении полуреакций.
Редокс-системы делят на два типа:
1. в системе осуществляется только перенос электронов: Fe 3+ +ē = Fe 2+ , Sn 2+ — 2ē = Sn 4+ . Это изолированное окислительно-восстановительное равновесие;
2. системы, когда перенос электронов дополняется переносом протонов, т.е. наблюдается совмещенное равновесие разных типов: протолитическое (кислотно-основное) и окислительно-восстановительное с возможной конкуренцией двух частиц протонов и электронов. В биологических системах важные редокс-системы относятся к этому типу.
Примером системы второго типа является процесс утилизации перекиси водорода в организме: Н2О2 + 2Н + + 2ē ↔ 2Н2О, а также восстановление в кислой среде многих окислителей, содержащих кислород: CrО4 2- , Cr2О7 2- , MnО4 — . Например, MnО4 — + 8Н + + 5ē = = Mn 2+ + 4Н2О. В данной полуреакции участвуют электроны и протоны.
Итак, окислительно-восстановительный потенциал (ОВП) – это потенциал системы, в которой активности окислительной и восстановительной форм данного вещества равны единице. ОВП измеряется с помощью окислительно-восстановительных электродов в сочетании со стандартными электродами сравнения.
В каждой окислительно-восстановительной реакции есть своя редокс-пара – эта пара имеет вещество в окисленной и восстановленной форме (Fe +3 /Fe +2 ).
Количественной мерой активности редокс-пары является величина ее ОВП.
Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать
Применение уравнения Нернста в решении задач.
При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:
Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:
Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.
Пример 1:
Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO4 и 0.01М ZnSO4 соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.
Решение:
Для начала запишем уравнения протекающих процессов:
Далее находим по таблице стандартные потенциалы процессов:
Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.
Найдем реальные потенциалы с учетом нестандартных активностей ионов:
Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:
Ответ: 1.13 В
Пример 2:
Одним из лабораторных способов получения хлора является действие KMnO4 на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?
Решение:
Для начала запишем уравнения протекающих процессов.
Далее находим по таблице стандартные потенциалы процессов:
Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:
Получается, что потенциал KMnO4 стал меньше, чем у хлора, а значит, реакция не пойдет.
Видео:ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать
Уравнение нернста адаптированное для биологических систем
Равновесие между химическими и электрическими движущими силами определяет величину мембранного потенциала покоя. Состояние равновесия достигается, когда различие в свободной энергии этих сил равно нулю (другими словами, когда общий поток = 0):
Изменение свободной энергии, происходящее при движении через мембрану компонента X, можно выразить уравнением:
• R — газовая постоянная (2 кал моль-1 К-1)
• Т — абсолютная температура (К; 37 °С = 307,5 К)
• [Х]0 — концентрация X вне клетки
• [X]i — концентрация X внутри клетки
и изменение свободной энергии, обусловленное транспортом через мембрану заряда, связанного с растворенным компонентом X составляет:
• Em — равновесный потенциал (в вольтах)
• z — валентность иона (электрический заряд)
• F— число Фарадея (2,3 х 104 кал вольт-1 моль-1)
В состоянии равновесия
и после преобразования получаем.
Таким образом, значение равновесного потенциала или потенциала Нернста для одновалентного иона X при 37 °С определяется уравнением:
Если концентрация ионов известна, то уравнение Нернста можно использовать для расчета равновесного мембранного потенциала для каждого иона в отдельности. На рисунке ниже показаны результаты таких расчетов для плазматической мембраны мышечных клеток. Так, для [К+]0 = 4 мМ и [K+]i = 155 мМ значение мембранного потенциала Еm = -98 мВ, если учитывать только поток ионов К+, т. е. Еm = Еk.
Почти во всех покоящихся клетках млекопитающих плазматическая мембрана проницаема для ионов К+. Na+/К+-АТФаза поддерживает трансмембранный ионный градиент и создает внутри клетки относительно высокую концентрацию ионов К+ ([K+]i). При открытии некоторых К+-каналов ионы К+ начинают транспортироваться в направлении градиента концентрации, что приводит к появлению положительного заряда с внешней стороны мембраны и отрицательного с внутренней ее стороны. Этот отрицательный мембранный потенциал, Еm, представляет собой электродвижущую силу, которая препятствует дальнейшему выходу К+ из клетки в направлении градиента (химическая движущая сила). Таким образом, открытие в покоящейся клетке специальных селективных К+-каналов определяет значение отрицательного потенциала покоя, при котором не происходит транспорта К+ через мембрану и величина Еm остается постоянной.
Аналогично потенциал Нернста можно рассчитать и для других ионов. Если мембрана становится более проницаемой для определенных ионов, то мембранный потенциал Еm будет меняться, приближаясь к значению потенциала Нернста для этих ионов (обычно становясь более положительным при деполяризации мембраны).
Например, если плазматическая мембрана становится более проницаемой для ионов Na+, то они будут транспортироваться в направлении своего градиента концентрации. При этом мембрана будет приобретать отрицательный заряд с внешней стороны и положительный заряд с внутренней. В физиологических условиях, в покоящейся клетке, открытие нескольких Na+-каналов, наряду с постоянным притоком зарядов за счет протечки, приведет к поступлению Na+ в клетку, и значение мембранного потенциала покоя сдвинется в более положительную сторону (например, -82 мВ). Напротив, аналогичный расчет в случае ионов К+ показывает, что значение мембранного потенциала покоя составит -89 мВ. В клетках, обладающих меньшей проницаемостью для ионов К+ в результате фоновой утечки ионов Na+ и деполяризующих ионных потоков, величина мембранного потенциала покоя Em смещается в сторону более положительных значений (например, становится равной -50 мВ). При возбуждении клетки электрическим зарядом и открытии Na+ каналов, в состоянии теоретического равновесия между потоком Na+, направленным в клетку, и потоком К+, направленным в противоположную сторону, уровень мембранного потенциала оказывается ближе к ENa, а не к Ек. Согласно уравнению Нернста, равновесный потенциал для Na+ при 37 °С составляет:
Если [Na+]0 = 145 мМ и [Na+]i = 12 мМ (как для клеток мышц), то значение мембранного потенциала составляет Еm = +67 мВ, принимая во внимание транспорт только ионов Na+. Таким образом, суммарный эффект открытия Na+ каналов выражается в установлении потока ионов натрия, направленного в клетку, что приводит к сдвигу отрицательного потенциала покоя Еm до значения +67 мВ.
Аналогичным образом, когда плазматическая мембрана становится более проницаемой для Са2+, ионы транспортируются в направлении градиента концентрации. При этом мембрана на внешней стороне приобретает более отрицательный заряд, а на внутренней — более положительный. Когда под действием электрического заряда клетка возбуждается и открываются Са2+-каналы, теоретическое равновесие между потоком Са2+ в клетку и потоком К+ из клетки определяет уровень мембранного потенциала ближе к значению ЕCa. Согласно уравнению Нернста,
Если [Са2+]0 = 1,5 мМ и [Ca2+]i = 0,1 мкМ, как для мышечной клетки, то мембранный потенциал составляет Em = +129 мВ. Таким образом, суммарный эффект открытия Са2+ каналов выражается в установлении потока Са2+ в клетку, который приводит к сдвигу отрицательного потенциала покоя Еm, к +129 мВ. [Са2+-каналы открываются при более положительном значении потенциала действия, чем натриевые каналы. Это означает, что они открываются на более поздней фазе потенциала действия. Для ионов Cl_ по уравнению Нернста получаем
Если [Cl-]0 = 123 мМ и [Cl-]i= 4,2 мМ, то мембранный потенциал только для Cl- составляет Еm = -90 мВ. Таким образом, суммарный эффект открытия хлоридного канала приводит к выходу ионов Cl-, что стабилизирует отрицательное значение потенциала покоя Еm.
Концентрация свободных ионов и равновесные потенциалы клеток скелетных мышц млекопитающих.
Значения равновесных потенциалов рассчитаны для 37 °С, принимая величину потенциала покоя мембраны мышечной клетки равной -90 мВ.
Сверху обозначены относительные радиусы негидратированных ионов.
Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021
📹 Видео
Гальванические элементы. 1 часть. 10 класс.Скачать
Потенциал покоя и равновесный потенциалСкачать
Лекция 4 Уравнение Нернста. Электрохимическое равновесиеСкачать
Уравнение Нернста. Условия изменения направления ОВР. Продукты в ОВР. Ч.5-3.Скачать
Уравнение НернстаСкачать
Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать
Составление схемы и вычисление ЭДС гальванического концентрационного элемента | Уравнение НернстаСкачать
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать
011 Электрохимия 4 уравнение НернстаСкачать
Потенциал покоя: - 70 мВ. Деполяризация, реполяризацияСкачать
ЕГЭ2020. ХИМИЯ. «Теория Льюиса. Механизмы органических реакций. Уравнение Нернста»Скачать
Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать
РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать
Электрохимия. Гальванический элемент Даниэля-ЯкобиСкачать
БЕЗ ЭТОГО НЕ СДАТЬ ЕГЭ по Химии — Электронная конфигурация атомаСкачать
Энтропия и второй закон термодинамики (видео 6) | Энергия| БиологияСкачать
Использование таблиц потенциалов и расчет ЭДС реакции. Продукты в ОВР. Ч.5-1.Скачать
