Из первого и третьего уравнений Максвелла вытекает важное соотношение, называемое уравнением непрерывности:
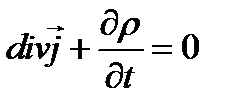
Правая часть уравнения (1.28) представляет собой сумму плотностей тока проводимости и тока смещения, т.е. плотность полного тока 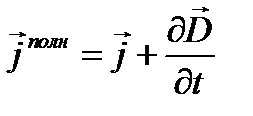
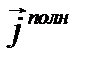
Уравнение (1.21) можно переписать
Уравнение (1.22) представляет собой закон сохранения заряда: всякому изменению величины заряда, распределенного в некоторой области, соответствует электрический ток I, втекающий в эту область или вытекающий из нее.
Граничные условия
Рассматриваемая на практике область может состоять из двух (и более) разнородных сред. На границе раздела сред параметры e, m и s меняются скачком. Соотношения, показывающие связь между значениями составляющих векторов электромагнитного поля в разных средах у поверхности раздела, называют граничными условиями. Данные соотношения получены по отдельности для нормальных (перпендикулярных) и тангенциальных (касательных) проекций электрических и магнитных векторов.
Граничное условие для нормальной составляющей вектора D в общем случае имеет вид:
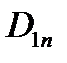
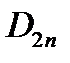
Здесь τ – поверхностная плотность заряда – характеризует заряд, распределенный вдоль поверхности раздела.
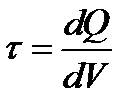
В случае если заряд не сосредоточен на поверхности раздела, т.е. не является поверхностным, то правая часть формулы (1.24) равна нулю, а нормальная компонента вектора D непрерывна при переходе из одной среды в другую:
Выражение (1.25) показывает, что при отсутствии на границе раздела двух сред поверхностных зарядов нормальная составляющая вектора электрического смещения меняется плавно, при наличии поверхностных зарядов – меняется скачкообразно.
Воспользовавшись материальным уравнением (1.4) можно получить граничное условие для напряженности электрического поля
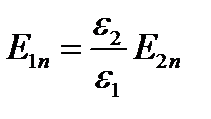
Выражение (1.26) показывает, что нормальная составляющая вектора напряженности электрического поля меняется скачком.
Граничное условие для нормальной составляющей вектора магнитной индукции имеет вид
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Выражая в равенстве (1.27) Bn через Нn, получаем
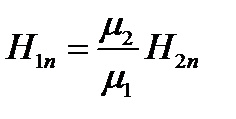
Граничное условие для касательных составляющих вектор напряженности магнитного поля имеет вид:
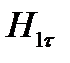
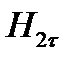
jsl – плотность поверхностного тока. Она определяется соотношением:
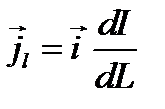
Выражение (1.30) характеризует токи, распределенные вдоль поверхности раздела в виде бесконечно тонкого слоя. Такие токи называют поверхностными.
В случае отсутствия поверхностных токов можем записать:
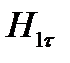
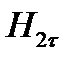
Выражение (1.31) показывает, что при отсутствии на границе раздела двух сред поверхностных токов касательная составляющая вектора напряженности магнитного поля меняется плавно, при наличии поверхностных токов – меняется скачкообразно.
Касательная составляющая вектора В, наоборот, претерпевает разрыв, величина которого определяется отношением магнитных проницаемостей:
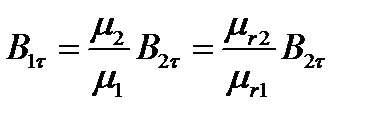
Граничное условие для касательной составляющей вектора Е:
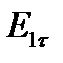
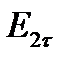
Касательная составляющая вектора Dпретерпевает разрыв, величина которого зависит от соотношения между диэлектрическими проницаемостями:
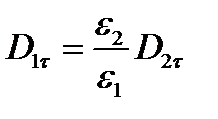
Уравнение непрерывности из уравнений максвелла
Основные уравнения классической электродинамики (система уравнений Максвелла) по праву являются общепризнанными уравнениями и широко применяются в физике, радиофизике и электронике. Однако эти уравнения не были получены из общих физических законов, что не позволяло считать их абсолютно точными, допускало различного рода манипуляции с ними. Тем не менее, эти уравнения точные и выводятся из общих принципов физики и основ векторной алгебры [1, 2].
1. Вывод закона электромагнитной индукции Фарадея
Закон электромагнитной индукции Фарадея можно получить из уравнения для электромагнитных сил, действующих на точечный электрический заряд [1, 2]:
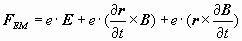 , , | (1) |
где e – заряд электрона, E – вектор напряженности электрического поля, r – радиальный вектор, соединяющий ось источника магнитной индукции B с электрически заряженной частицей и лежащий в плоскости, ортогональной оси симметрии магнитного поля.
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Рассмотрим случай, когда магнитная часть силы FЕМ равна и направлена противоположно ее электрической части:
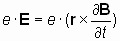 . . | (2) |
Такая ситуация возникает в проводнике с электрическим током высокой частоты, когда сила, действующая на электрон со стороны первичного электрического поля изменяется настолько быстро, что оказывается в противофазе с силой инерции электронов.
Сократим заряд в равенстве (2) и применим к обеим частям этого равенства операцию «ротор»:
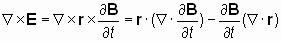 . . | (3) |
Пусть, например, ось z совпадает с направлением аксиального вектора B, тогда радиус-вектор будет иметь вид: r=xi+yj, где i и j – единичные векторы в направлениях осей координат x и y, соответственно. Радиальный векторr не имеет третьей составляющей вдоль оси z, поэтому второе слагаемое в (3) равно –2(∂B/∂t). Первое же слагаемое в уравнении (3) равно ∂B/∂t. В результате, после преобразования правой части последнего равенства, получаем:
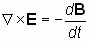 . . | (4) |
То есть из электромагнитного силового уравнения (1) в том случае, когда сила, действующая на электрон со стороны магнитного поля, полностью уравновешивается силой со стороны электрического поля, следует закон электромагнитной индукции Фарадея (4), − одно из основных уравнений электродинамики.
Уравнения (2) – (4) не зависят от того, имеется или отсутствует электрон в данной точке пространства. В результате такой независимости электрического и магнитного полей от электрического заряда уравнение (4) отражает пространственно-временные свойства самих изменяющихся полей, представимых в виде единого электромагнитного поля. При этом закон Фарадея (4) не только представляет собой закон электромагнитной индукции, но является и основным законом взаимного преобразования электрического и магнитного полей, − неотъемлемым свойством электромагнитного поля.
2. Вывод уравнения Максвелла
Прежде, чем приступить к выводу уравнения Максвелла, необходимо дополнить векторную алгебру еще одним векторным оператором.
2.1. Определение векторного оператора, выполняющего действие, обратное векторному преобразованию дифференциального векторного оператора «ротор»
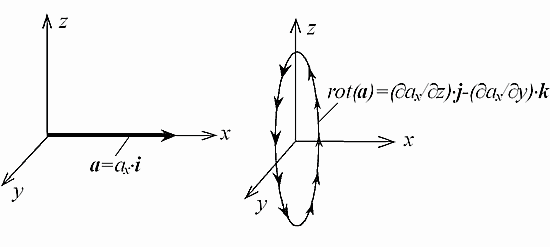
Дифференциальный векторный оператор «ротор» выполняет операцию преобразования векторов в пространстве и операцию дифференцирования, то есть является сложным оператором, осуществляющим сразу два вида действий. Это прямо следует из его определения [3]:
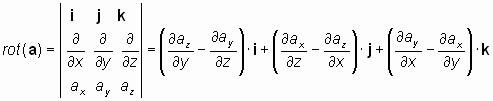
где а – вектор, i, j, k – единичные векторы в направлении осей прямоугольной (декартовой) системы координат x, y и z, соответственно. При этом оператор, обратный оператору «ротор», в векторном анализе не определен, хотя каждое из выполняемых им преобразований, в принципе, обратимо.
Геометрическая иллюстрация пространственного преобразования вектора а в вектор rot(a), осуществляемая оператором «ротор», показана на Рис. 1.
Рис. 1. Геометрическое представление вектора а и векторного поля, образованного оператором «ротор».
2.2. Определение 1. Если два взаимосвязанных векторных поля, представленные векторами а и b, имеют производные по пространственным переменным x, y, z (в виде rotaи rotb)и производные по времени, ¶ а/ ¶ t и ¶ b/ ¶ t, причем производная вектора а по времени ортогональна производным по пространственным переменным вектора b, и наоборот, производная по времени вектора b ортогональна производным по пространственным переменным вектораа, то существует векторный оператор, осуществляющий пространственное преобразование векторного поля, не затрагивающее операцию дифференцирования, который условно назовем оператором «rerot», (противоположно закрученный или «реверсивный ротор») такой, что:
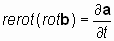
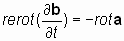
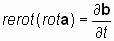
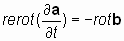
Видео:Лекция 2. Уравнение неразрывностиСкачать

2.3. Свойства векторного оператора «реверсивный ротор»
2.3.1. Векторный оператор «реверсивный ротор» действует только на производные вектора.
2.3.2. Векторный оператор «реверсивный ротор» располагается перед производной вектора, на которую он действует.
2.3.3. Константы и числовые коэффициенты при производных вектора могут быть вынесены за пределы действия векторных операторов:
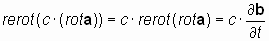

2.3.4. Векторный оператор «реверсивный ротор» действует на каждое из слагаемых уравнения, содержащего сумму векторных производных:
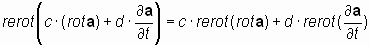
2.3.5. Результат действия векторного оператора «реверсивный ротор» на ноль есть ноль:
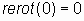
При этом результат действия векторного оператора «реверсивный ротор» на другие константы, в том числе на вектор, согласно пункту 2.3.1, не определен.
2.4. Пример применения оператора «реверсивный ротор»
Применим оператор «реверсивный ротор» к уравнению, содержащему взаимосвязанные векторы a и b:
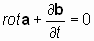 . . | ((*)) |
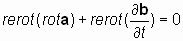
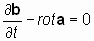 . . | ((**)) |
Если теперь еще раз применить оператор «реверсивный ротор» к вновь образованному равенству (**), то получим:

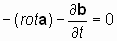
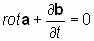 . . | ((*)) |
Последовательное двойное (или любое четное) применение оператора «реверсивный ротор» приводит к исходному равенству. Этим самым векторный оператор «реверсивный ротор» осуществляет не только взаимное преобразование дифференциальных уравнений взаимосвязанных векторных полей, но и устанавливает эквивалентность этих уравнений.
Геометрически это выглядит так. Оператор «ротор» дифференцирует и как бы закручивает прямолинейное векторное поле, делая его вихревым и ортогональным исходному векторному полю. Векторный оператор «реверсивный ротор» выполняет векторное преобразование, которое как бы раскручивает вихревое поле, закрученное оператором «ротор», превращая его в изменяющееся невихревое поле, представленное производной вектора по времени. Поскольку интегрирование не производится, производная вектора по времени соответствует изменению величины вектора. В результате имеем изменение вектора, величина которого изменяется в единственном направлении, ортогональном пространственным переменным оператора «ротор». И наоборот, векторный оператор «реверсивный ротор» закручивает невихревое изменяющееся векторное поле, представленное производной вектора по времени, превращая его в вихревое пространственное векторное поле, ортогональное исходной производной вектора по времени. Так как направление «кручения» оператора «реверсивный ротор» противоположно направлению вращения, осуществляемому оператором «ротор», то знак вновь образованного вихревого поля выбирается противоположным (отрицательным). То есть векторный оператор «реверсивный ротор» выполняет действие, обратное пространственному преобразованию оператора «ротор» на всем «пространстве» производных векторных полей. В то же время векторный оператор «реверсивный ротор» сам не дифференцирует вектор, на производную которого он действует. Этим самым осуществляется тождественное обратимое векторное преобразование.
Видео:Ацюковский: Уравнения Максвелла эту задачу не решают!Скачать

Если ввести в векторный анализ интегральный векторный оператор, восстанавливающий не производную вектора, а сам вектор из ротора вектора (условно назовем такой оператор обратным ротором, или «rot -1 »), то такой оператор наряду с обратным векторным преобразованием одновременно должен производить операцию интегрирования.
Однако, в силу неоднозначности математической операции интегрирования, полностью обратный «ротору» оператор rot -1 не осуществляет однозначное обратное векторное преобразование.
2.5. Применение векторного оператора «реверсивный ротор» к физическим полям
При применении векторного оператора «реверсивный ротор» к физическим векторным полям необходимо учитывать изменение размерности правой и левой частей уравнения из-за перестановки переменных x, y, z и t при преобразовании. Обозначим размерность координат – метр (L), а времени – секунда (T).
Определение 2. Для физических векторных полей векторный оператор «реверсивный ротор», определяется следующим образом:
и 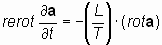 ; ; | (6) |
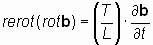
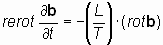
Обозначая размерное отношение L/T, как константу v, имеющую размерность скорости, [м/с], уравнения (6.4) и (6.4*) можно представить в виде:
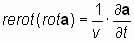 и и 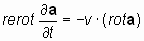 ; ; | (7) |
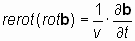 и и 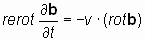 . . | (7*) |
2.6. Применение оператора «реверсивный ротор» к физическим полям
Применим векторный оператор «реверсивный ротор», определенный уравнениями (7), (7*), к уравнению (4), связывающему реальные физические поля E и B в электродинамике:
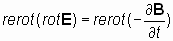

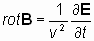 | (8) |
Электродинамическая постоянная «v» не зависит ни от величины полей, ни от скорости их изменения и, как следует из волнового уравнения, соответствует скорости распространения волны электромагнитного взаимодействия, c » 2.99792458 Ч 10 8 м/c, которая называется также скоростью света в вакууме.
То есть с помощью векторного преобразования «реверсивный ротор» из уравнения (4), представляющего собой закон электромагнитной индукции Фарадея, естественным образом вытекает одно из основных уравнений электродинамики — уравнение Максвелла (8), которое не следует ни из эксперимента, ни из известных физических законов. Уравнения (4) и (8) являются взаимосвязанными, трансформируемыми друг в друга при помощи векторного преобразования, что соответствует их физической эквивалентности. Поэтому справедливость одного из этих уравнений, установленная в виде физического закона (в данном случае — это закон электромагнитной индукции Фарадея (4)) является достаточным условием для утверждения о справедливости второго уравнения (уравнения Максвелла (8)) в качестве эквивалентного физического закона.
2.7. Трансформация векторных полей
Если исходить из определения оператора «ротор», то действие векторного оператора «обратный ротор», казалось бы, можно представить в виде, показанном на Рис. 2, где предполагается некоторая тождественность векторных полей до и после векторного преобразования дифференциальным векторным оператором «ротор».
Проверим это предположение. Применим оператор «реверсивный ротор» к уравнению:
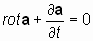
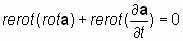

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Полученное равенство изменяет направление векторов в исходном определении дифференциального векторного оператора «ротор», что недопустимо.
Поэтому 
Применение векторного оператора «реверсивный ротор» к производным одного и того же векторного поля показывает принципиальное различие между векторным полем до применения, и векторным полем после применения оператора «ротор». Это означает необходимость представлять поле вектора а и поле вектора rot(а) как трансформируемые друг в друга, но различные векторные поля.
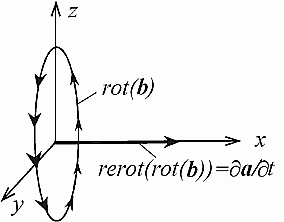
Исходное векторное поле, представленное вектором а, будем считать первичным (причиной), а поле, образованное векторным преобразованием оператора «ротор», будем считать вторичным полем (следствием действия оператора «ротор») и обозначим его, как поле векторов b.
Рис. 2. Результат отождествления векторных полей до и после векторного преобразования «ротор». Направление полей не соответствует исходному определению оператора «ротор», показанному на Рис. 1, «правый винт» превращается в «левый винт».
Тогда обратное преобразование векторных полей, не затрагивающее операции дифференцирования, во введенных таким образом обозначениях будет иметь вид, показанный на Рис. 3.
Рис. 3. Определение векторного преобразования, обратного операции «ротор», не затрагивающего операции дифференцирования. Разделение векторных полей выполнено по признаку причинно-следственных отношений. Исходное поле представлено вектором а (причина), а поле, образованное операцией «ротор», представлено вектором b (следствие).
В электродинамике в некоторых простейших случаях переход к вращающейся системе отсчета, внутри которой исчезает вращение, приводит к отсутствию сил со стороны магнитного поля, и силовое воздействие может быть представлено только силой со стороны электрического поля. Но из этого никак не следует вывод, что магнитного поля нет или оно всегда может быть заменено электрическим полем. Частный случай векторного поля, взятого в отдельной изолированной системе отсчета, относится только к данной выбранной системе, в которой осуществляется ограниченное по степеням свободы движение электрического заряда.
Поскольку в пространстве существуют и прямолинейные векторные поля, и вращающиеся замкнутые векторные поля, а находиться в двух системах отсчета одновременно невозможно, то в общем случае выбором системы координат нельзя свести одно поле к другому. Источник этих полей один – это электрические заряды. Электрические заряды создают вокруг себя электрическое поле (всесторонне направленное векторное поле), а движение электрических зарядов создает магнитное поле (замкнутое круговое векторное поле). При этом, естественно, прямолинейное движение электрических зарядов создает вокруг них круговое магнитное поле, а круговое движение электрических зарядов (равно как вращение электрически заряженных частиц вокруг собственной оси) создает прямолинейное в пространстве магнитное поле, заключенное в объеме, ограниченном радиусом вращения.
2.8. Скорость распространения электромагнитного взаимодействия
Скорость преобразования векторных полей друг в друга не зависит ни от величины полей, ни от скорости их изменения и, как следует из волнового уравнения, соответствует скорости распространения волны электромагнитного взаимодействия в свободном пространстве (вакууме),c » 2.99792458 Ч 10 8 м/c, и эта величина по праву называется электродинамической постоянной.
Таким образом, изменение электрического и магнитного полей, осуществляемое в трехмерном пространстве, имеет свойство взаимного преобразования векторов, и это свойство в электродинамике осуществляется посредством закона электромагнитной индукции Фарадея. Если считать такое преобразование прямым, то обратное преобразование векторных полей осуществляется при помощи уравнения, полученного Максвеллом интуитивным путем, и которое можно получить при помощи векторного оператора «реверсивный ротор». Взаимное преобразование электрического и магнитного полей, которое осуществляется без источников электрического заряда, представляет собой один из особых видов волнового движения — поперечную электромагнитную волну, которая переносит электромагнитную энергию в свободном пространстве с абсолютной скоростью преобразования полей. Но при этом источником энергии электромагнитной волны всегда являются ускоренно движущиеся электрические заряды.
3. Уравнения источников электромагнитных полей.
Оставшиеся два из четырех основных уравнений системы уравнений Максвелла лишь устанавливают факт наличия в природе электрических зарядов, создающих электрическое поле (теорема Гаусса, которая прямо следует из закона Кулона):
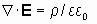
и факт отсутствия в природе магнитных зарядов:
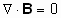
Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Литература
- Сокол-Кутыловский О.Л. Гравитационные и электромагнитные силы. Екатеринбург, 2005.
- Сокол-Кутыловский О.Л. Русская физика. Екатеринбург, 2006.
- Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗОВ (под редакцией Г. Гроше и В. Циглера), М., «Наука», 1980.
🔥 Видео
Вывод уравнения неразрывности - Лекция 1Скачать

Уравнение непрерывности и телеграфное уравнение | Лекция 31 | МатанализСкачать

Вывод уравнений МаксвеллаСкачать

Вывод некоторых уравнений математической физики из уравнений Максвелла.Скачать

3 14 Уравнения МаксвеллаСкачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Уравнения Максвелла и соответствующие уравнения Волновой МоделиСкачать

Уравнения Максвелла Лекция 10-1Скачать

60. Уравнения МаксвеллаСкачать

Лекция №9. Уравнения МаксвеллаСкачать

Уравнения Максвелла 2021Скачать

Система уравнений Максвелла. Связь интегральной и дифференциальной формы уравнений.Скачать

1.1. Решение системы уравнений Максвелла методом интегральных преобразованийСкачать