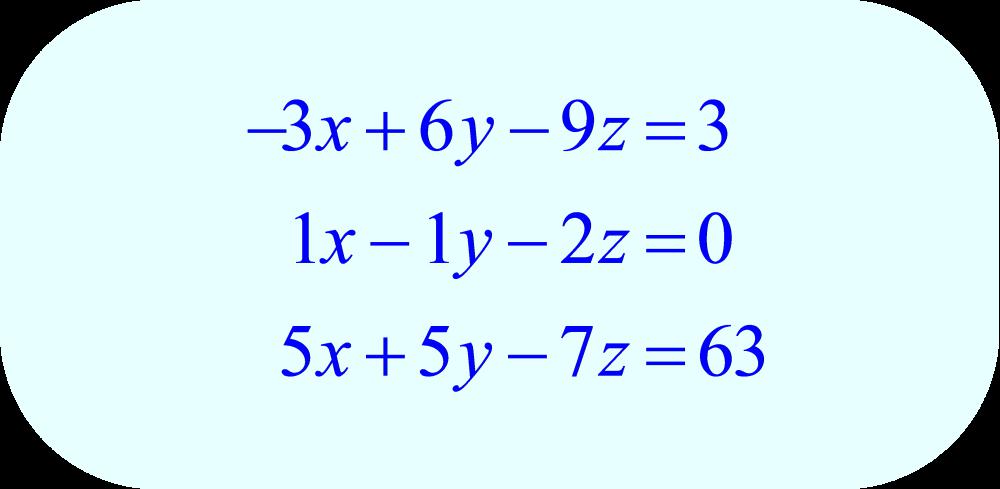Уравнение не имеет действительных корней

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Видео:Доказать, что уравнение не имеет положительных корнейСкачать

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

1. Линейное уравнение

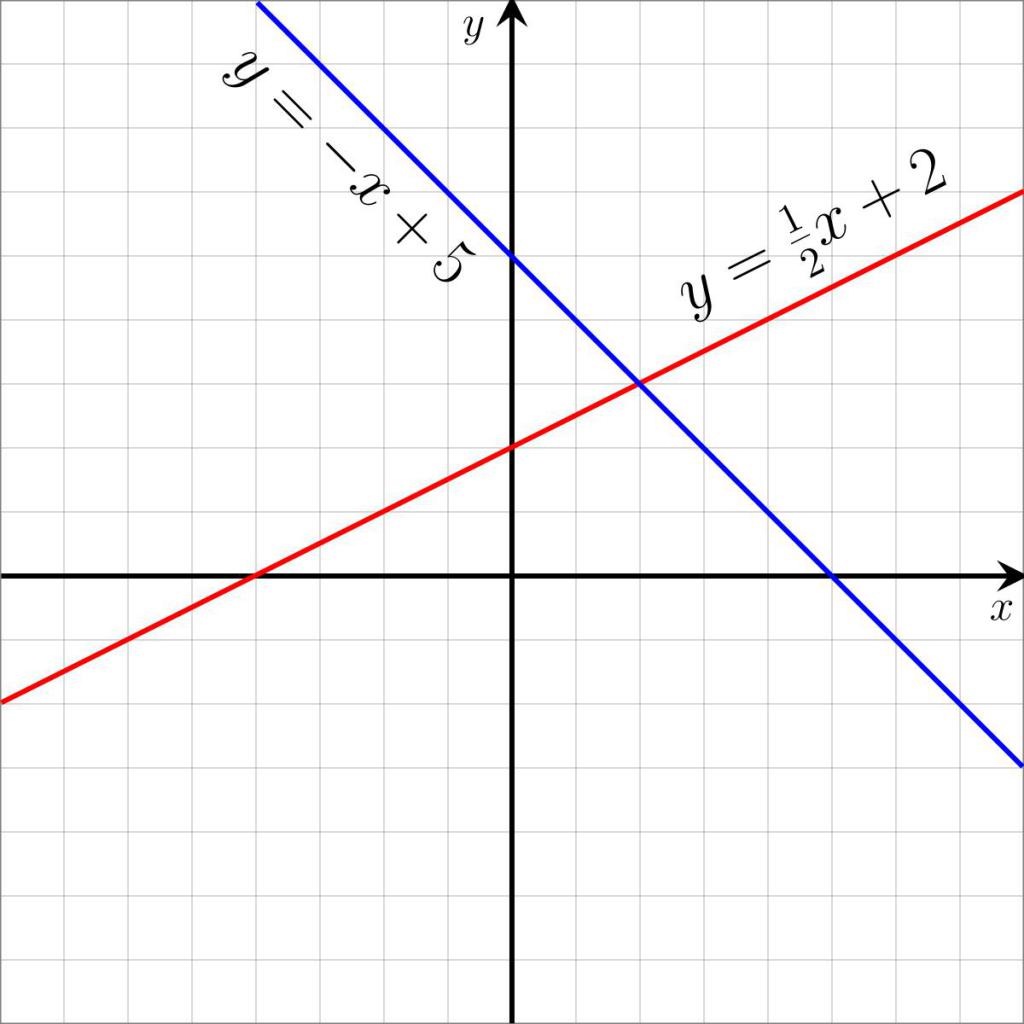
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

Видео:Имеет ли уравнение действительные корни?Скачать

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х_1,2= (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

Видео:✓ Батл! Восьмиклассник против первокурсника: Кто решит проще? | Ботай со мной #086​ | Борис ТрушинСкачать

3. Тригонометрические уравнения

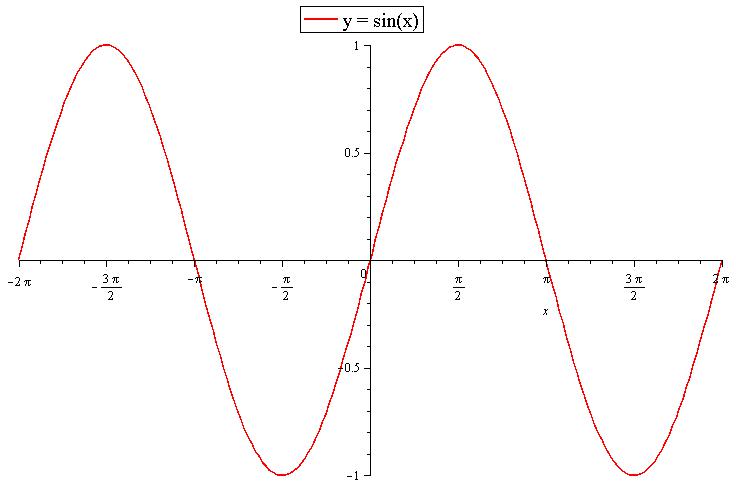
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

Видео:Найдите сумму действительных корней уравненияСкачать

Обобщение и советы по нахождению корней уравнения

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

• в линейном уравнении mx = n значение m = 0 и n = 0;
• в квадратном уравнении, если дискриминант меньше нуля;
• в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
• в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Если и – корни квадратного уравнения
, то по теореме Виета:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

3) Найдите все значения , при каждом из которых все решения уравнения

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

С учетом пункта 1 получим ответ

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Сделаем замену

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

Объединив все случаи, получим ответ.

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Решение (корни) квадратного уравнения

Видео:✓ Про степень с действительным показателем | В интернете опять кто-то неправ #005 | Борис ТрушинСкачать

Определение квадратного уравнения и общее понятие о его корнях

Квадратным уравнением называется уравнение вида ax² + bx + c = 0 , где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0 .

Например, квадратным является уравнение

В квадратном уравнении ax² + bx + c = 0 коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.

Уравнения вида ax² + bx = 0 ,

называются неполными квадратными уравнениями.

Найти корни квадратного уравнения значит решить квадратное уравнение.

Для вычисления корней квадратного уравния служит выражение b² — 4ac , которое называется дискриминантом квадратного уравнения и обозначается буквой D.

Корни квадратного уравнения имеют следующие сферы применения:

— для разложении квадратного трёхлена на множители, что, в свою очередь, является приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.д.) в частности, при нахождении пределов, производных и интегралов;

— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения, чаще всего один, являются обычно конечным решением).

Видео:311 Алгебра 9 класс. При каких значениях t Уравнение не имеет корнейСкачать

Геометрический смысл решения квадратного уравнения

График квадратичного трёхлена ax² + bx + c — левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна оси 0y . Число точек пересечения параболы с осью 0x определяет число корней квадратного уравнения. Если точек пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает ось 0x , то квадратное уравнение не имеет действительных корней. На рисунке ниже изображены три упомянутых случая.

Как видно на рисунке, красная парабола пересекает ось 0x в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью 0x .

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Три случая после нахождения дискриминанта квадратного уравнения

1. Если дискриминант больше нуля (), то квадратное уравнение имеет два различных действительных корня.

Они вычисляются по формулам:

и

.

Часто пишется так: .

2. Если дискриминант равен нулю (), то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня, которые равны .

3. Если дискриминант меньше нуля (), то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней в этой статье рассматривать не будем. В общем случае правильным решением является констатация того, что квадратное уравнение не имеет действительных корней.

Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.

Путём преобразования в квадратное уравнение следует решать и дробные уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, . О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.

Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.

Пример 3. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Решение полных квадратных уравнений

Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Пример 4. Найти корни квадратного уравнения:

.

В примере 1 нашли дискриминант этого уравнения:

,

Решение квадратного уравнения найдём по формуле для корней:

Пример 5. Найти корни квадратного уравнения:

.

В примере 2 нашли дискриминант этого уравнения:

.

Применим формулу корней квадратного уравнения . Отсюда , . Найденные корни квадратного уравнения равны друг другу, а это значит, что уравнение имеет единственный корень:

Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Корни приведённого квадратного уравнения

Пусть дано квадратное уравнение . Так как , то разделив обе части данного уравнения на a, получим уравнение . Полагая, что и , приходим к уравнению , в котором первый коэффициент равен 1. Такое уравнение называется приведённым.

Формула корней приведённого уравнения имеет вид:

.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Теорема Виета

Существуют формулы, связывающие корни квадратного уравнения с его коэффициентами. Они впервые были получены французским математиком Ф.Виетом.

Теорема Виета. Если квадратное уравнение ax² + bx + c = 0 имеет действительные корни, то их сумма равна — b/a , а произведение равно с/a :

Следствие. Если приведённое квадратное уравнение x² + px + q = 0 имеет действительные корни и , то

Пояснение формул: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Следовательно, теорему Виета можно применять и для поиска корней приведённого квадратного уравнения.

Пример 6. Написать приведённое квадратное уравнение, корнями которого являются числа 1 и -3.

Иначе говоря, надо найти числа p и q такие, чтобы квадратное уравнение

имело корни и .

По формулам Виета , . Требуемое в условии задачи уравнение имеет вид

Видео:Как считать корни? #shortsСкачать

Решение неполных квадратных уравнений

Пример 7. Решить квадратное уравнение .

Решение. Чтобы решить данное неполное квадратное уравнение, разложим его левую часть на множители. Получим

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю: или . Решая уравнение , находим .

Следовательно, произведение обращается в нулю при и при . Поэтому числа 0 и 1/2 являются корнями неполного квадратного уравнения .

Пример 8. Решить квадратное уравнение .

Решение. Чтобы решить данное неполное квадратное уравнение, перенесём в его правую часть свободный член с противоположным знаком и разделим обе части уравнения на 3. Получим уравнение

.

Так как , то уравнение не имеет действительных корней. Следовательно, не имеет действительных корней и эквивалентное ему неполное квадратное уравнение .

Видео:Вариант 40, № 2. Линейное уравнение, не имеющее корнейСкачать

Разложение квадратного трёхчлена на множители с применением корней квадратного уравнения

Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно разложить на множители по следующей формуле:

.

Этот приём часто используется для упрощения выражений, особенно сокращения дробей.

Пример 9. Упростить выражение:

.

Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:

.

Корни квадратного уравнения будут следующими:

.

Разложим квадратный многочлен на множители:

.

Упростили выражение, проще не бывает:

.

Пример 10. Упростить выражение:

.

Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:

.

Корни первого квадратного уравнения будут следующими:

.

Находим дискриминант второго квадратного уравнения:

.

Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:

.

Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:

.

Упрощать выражения путём решения квадратных уравнений требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде, он может быть получен в процессе предварительных преобразований выражения.

Видео:Уравнение из МФТИ Эпичный косякСкачать

Из истории решения квадратных уравнений

Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39 ).

Площадь большого квадрата равна (x + 5)² . Она складывается из площади x² + 10x заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх квадратов со стороной 5/2 , равной 25. Получается следующее уравнение и его решение:

Видео:90 россиян решат это уравнение за пять минут. Уравнение с параметромСкачать

Различные прикладные задачи на квадратные уравнения

Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?

Решение. Примем количество ткани в отрезке за x и получим уравнение:

Приведём обе части уравнения к общему знаменателю:

Произведём дальнейшие преобразования:

Получили квадратное уравнение, которое и решим:

Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.

Ответ: в отрезке 20 м ткани.

Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках. Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом 2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?

Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:

Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение. Процесс записывается так:

Найдём корни квадратного уравнения:

Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.

Ответ: в одном ящике взвешивают 12,5 кг ткани.

🎬 Видео

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Рациональные корни многочлена с целым показателем. 10 класс.Скачать

Схема Горнера. 10 класс.Скачать