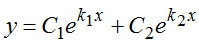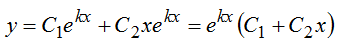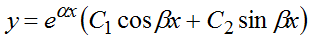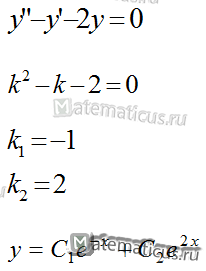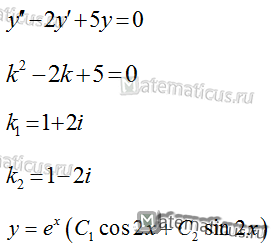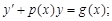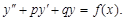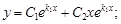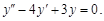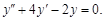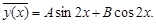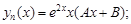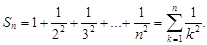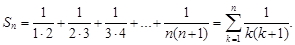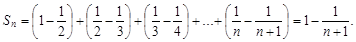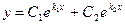Если дифференциальное уравнение имеет вид:
y′′ + py’ + qy = 0
то такое уравнение называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
p, q — числа или постоянные коэффициенты
Для решения искомого уравнения необходимо записать характеристическое уравнение вида
k 2 + pk + q = 0
Корни характеристического уравнения можно найти через дискриминант
D = p 2 – 4q
В характеристическом уравнении три случая различных корней, перечислим их:
- Если D>0, то уравнение имеет два действительных и различных корня:
k1, k2 – корни уравнения
тогда запишем общее решение уравнения: 
II. Если D=0, то уравнение имеет один действительный корень:
k – корень уравнения
отсюда получим общее решение уравнения: 
k1,2 = α ±i β
k1, k2 – корни уравнения
α — действительная часть корня
β — мнимая часть корня
запишем общее решение уравнения: 
Пример 1 
Найдите общее решение дифференциального уравнения второго порядка с постоянными коэффициентами:
Пример 3 
- Дифференциальные уравнения второго порядка
- Дифференциальные уравнения второго порядка.
- I. Уравнение, не содержащее явно переменную $у$
- II. Уравнение, не содержащее явно переменную $х$
- III.Линейные дифференциальные уравнения второго порядка
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- 🎦 Видео
Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать
Дифференциальные уравнения второго порядка
1) Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами p и q называется уравнение вида
(8)
Алгебраическое уравнение k 2 + pk + q = 0 называется характеристическим уравнением для данного дифференциального уравнения, а его корни – характеристическими числами (корнями).
Для нахождения общего решения уравнения (8):
1. Запишем соответствующее характеристическое уравнение
2. В соответствии со знаком дискриминанта возможны три случая:
а) D > 0. Тогда характеристическое уравнение имеет два действительных корня k1 ¹ k2, и общее решение уравнения (8) имеет вид
(9)
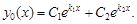
б) D = 0. Тогда k = k1 = k2 – действительный корень и общее решение уравнения (8) имеет вид
(10)
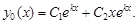
2) 
3) 
1. Запишем характеристическое уравнение k 2 + k – 2 = 0.
Найдем его корни
; k1 = –2; k2 = 1.
Так как k1 ¹ k2 – действительные числа, то общее решение находим по формуле (9)
2. Запишем характеристическое уравнение k 2 + 2k + 1 = 0.
Найдем его корни
В этом случае общее решение находим по формуле (10)
3. Запишем характеристическое уравнение k 2 + 4k + 5 = 0.
Найдем его корни
Здесь 
Общее решение находим по формуле (11)
Тест 19. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является уравнение вида:
1) 
2) 
3) 
4) 
5) 
Тест 20. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является:
1) 
2) 
3) 
4) 
5) 
Тест 21. При решении однородного дифференциального уравнения второго порядка с постоянными коэффициентами 
= 0:
1) вводится подстановка вида y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции;
2) вводится подстановка вида y = u × x, где u = u(x) – некоторая неизвестная функция;
3) составляется характеристическое уравнение k 2 + pk + q = 0.
Тест 22. Характеристическое уравнение k 2 + pk + q = 0 имеет два различных действительных корня k1 и k2. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 
имеет вид:
1) 
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 
4) 
Тест 23. Характеристическое уравнение k 2 + pk + q = 0 имеет комплексные корни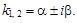 
Тогда общее решение однородного диф-
ференциального уравнения второго порядка с постоянными коэффициентами имеет вид:
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3)
4)
Тест 24. Характеристическое уравнение k 2 + pk + q = 0 имеет равные корни k1 = k2. Тогда общее решение однородного дифферен-
циального уравнения второго порядка с постоянными коэффициентами имеет вид:
1) 
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 
4)
Тест 25. Характеристическое уравнение k 2 + pk + q = 0 имеет комплексные корни 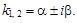Тогда общее решение однородного диф-
ференциального уравнения второго порядка с постоянными коэффициентами имеет вид:
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3)
4)
Тест 26. Характеристическое уравнение k 2 + pk + q = 0 имеет D = 0. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами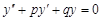 
имеет вид:
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 
4)
Тест 27. Характеристическое уравнение k 2 + pk + q = 0 имеет D 2 + Bx + C и т. д.
Пример 10. Определить вид частного решения уравнения
Запишем соответствующее однородное уравнение
1. Характеристическое уравнение k 2 – 4k + 3 = 0 имеет корни k1 = 1; k2 = 3.
2. В правой части данного уравнения функция вида (13)
3. Здесь a = 2 – не является корнем характеристического уравнения; 
– многочлен первой степени.
Следовательно, частное решение данного неоднородного уравнения надо искать в виде (14), т. е. 
= e 2x (Ax + B).
2. Пусть в правой части уравнения (12) функция
f(x) 
(17)
Тогда частное решение уравнения (12) будем искать в виде решений, приведенных в таблице 5.
| Если a ± bi не являются корнями соответствующего характеристического уравнения | Если a ± bi – корни характеристического уравнения |
 (18) |  (19) |
Пример 11. Определить вид частного решения уравнения
Запишем соответствующее однородное уравнение
1. Характеристическое уравнение k 2 + 4k – 2 = 0 имеет корни 
2. В правой части данного уравнения функция вида (17)
f(x) 
т. е. f(x) 
3. Здесь a = 0; b = 2. Составленные из этих значений комплексные числа a ± bi = 0 ± 2i не являются корнями характеристического уравнения.
Следовательно, частное решение данного неоднородного уравнения надо искать в виде (18), т. е.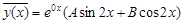 
или 
Тест 34. Характеристическое уравнение k 2 – 4k + 3 = 0, соответ-
ствующее однородному дифференциальному уравнению второго порядка с постоянными коэффициентами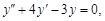 
имеет корни k1 = 1; k2 = 3. Тогда частное решение соответствующего неоднородного уравнения 
имеет вид:
1) 
2) 
3) 
4) 
5) 
Тест 35. Характеристическое уравнение k 2 – 4k + 4 = 0, соответ-
ствующее однородному дифференциальному уравнению второго порядка с постоянными коэффициентами 
имеет корень k = 2. Тогда частное решение соответствующего неоднородного уравнения 
имеет вид:
1)
2)
3)
4)
5)
После того, как вид частного решения определен, методом неопределенных коэффициентов находим коэффициенты A и B.
Ответы на тестовые задания
| Номер теста |
| Правильный ответ |
Ряды
Числовые ряды
Пусть дана числовая последовательность 
.
(1)
называется числовым рядом, или просто рядом.
Числа 
называются членами ряда, член an с произвольным номером – общим членом ряда.
Суммы конечного числа членов ряда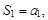 
…, 
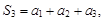
… называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм
(2)
Пример 1. Пусть дана числовая последовательность
. (3)
Тогда последовательность 
будет иметь вид
…, 
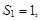
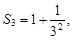
Последовательности (3) соответствует ряд
(4)
Пример 2.Рассмотрим ряд
(5)
Найдем его частичную сумму Sn. Имеем
Его частичную сумму можно упростить, если заметить, что
Тест 1. Определить второй член ряда 
1) 
2) 
3) 
4) 
5) 
Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу S, которое называется суммой ряда (1). Символически
Если же последовательность частичных сумм (2) расходится, то ряд (1) называется расходящимся. Такой ряд суммы не имеет.
Тест 2.Определить частичную сумму S3 ряда 1 + 
+ 
+ 
+… :
1) 
2) 
3) 
4) 
Простейшими примерами числовых рядов, вопрос о сходимости которых решен, являются следующие ряды:
1. 
– геометрический ряд, который при 
1 сходится, при α ≤ 1 расходится.
Пример 3.Исследовать сходимость ряда 
+ + 
+…+ 
+… .
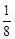
Это геометрический ряд, так как q = 1;
5) при 
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Дифференциальные уравнения второго порядка.
В дифференциальном уравнении второго порядка [Fleft( right) = 0] выразим вторую производную:
Теорема о существовании и единственности решения уравнения (*). Если в некоторой области $D$ функция $fleft( right)$ и ее частные производные непрерывны, то для любой точки $left( <,,<_0>> right) in D$ существует единственное решение $y = varphi left( x right)$ удовлетворяющее начальным условиям:[ = varphi left( <> right);<_0> = varphi ‘left( <> right).]
Общим решением уравнения (*) называется функция [y = varphi left( <x,,> right),]зависящая от произвольных постоянных $<,>$ и удовлетворяющая условиям:
- при любых значениях постоянных $ <= ^ * , = ^ * >$ функция $y = varphi left( <x,^ * ,^ * > right),$ является решением уравнения (*);
- для любой точки $left( <,,<_0>> right) in D$ существуют значения постоянных $ <= ^ * , = ^ * >$, что $ = varphi left( <x,^ * ,^ * > right),^prime = varphi ‘left( <x,^ * ,^ * > right).$
Рассмотрим типы уравнений второго порядка.
I. Уравнение, не содержащее явно переменную $у$
Решение этого уравнения сводится к решению двух уравнений первого порядка. Для этого сделаем замену $y’ = gleft( x right),y» = g’left( x right).$ Получим систему из двух уравнений [left< begin
Fleft( right) = 0 hfill \
y’ = gleft( x right) hfill \
end right.]В первую очередь решаем первое уравнение, и, подставляя полученное решение во второе уравнение, определяем искомую функцию.
II. Уравнение, не содержащее явно переменную $х$
В этом случае вводим новую функцию, зависящую от $y$:[y’ = pleft( y right),y»left( x right) = p cdot frac<><>.]
III.Линейные дифференциальные уравнения второго порядка
Рассуждения данного раздела могут быть применены и для подобных уравнений более высокого порядка.
В общем случае линейное дифференциальное уравнение второго порядка может быть записано в следующем виде:
$y» + a(x)y’ + b(x)y = fleft( x right)$ (**)
В случае равенства правой части тождественно нулю уравнение называется однородным, в противном случае неоднородным. Рассмотрим в начале однородные уравнения.
1. Линейным однородным уравнением второго порядка называется уравнение
$y» + a(x)y’ + b(x)y = 0$ (1**)
Рассмотрим некоторые свойства этих уравнений.
Теорема 1. Если функции $y = left( x right),$ $y = left( x right)$ — два решения данного уравнения, то их линейная комбинация [y = left( x right) + left( x right)] тоже является решением этого уравнения.
Функции $left( x right),left( x right). left( x right)$ — называются линейно независимыми на отрезке $left[ right]$, если их линейная комбинация $left( x right) + left( x right) + . + left( x right)$ ни при каких значениях $$, кроме случая $ equiv 0,forall i$, не обращается в ноль (для всех значений $x in left[ right]$).
В противном случае функции называются линейно зависимыми.
Теорема 2. Если $left( x right)$ и $left( x right)$- два линейно независимых решения уравнения (1**), то общее решение представимо в виде линейной комбинации данных частных решений[y = cdot left( x right) + cdot left( x right)]
2. Линейное неоднородное дифференциальное уравнение второго порядка
Общее решение неоднородного уравнения[Fleft( right) = fleft( x right)]
может быть представлено в виде суммы общего решения соответствующего однородного уравнения (1**) и некоторого частного решения неоднородного уравнения[<y_> = <y_> + <y_>.]
3.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Если коэффициенты $p$ и $q$ постоянны, т.е. не зависят от $x$, то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:
Решение уравнения будем искать в следующем виде $y = <e^>$. Подставив данную функцию в уравнение (2**), будем иметь [<e^> + pk<e^> + q<e^> = 0] или [ + pk + q = 0] т.к. экспонента никогда не может обратиться в ноль.
Уравнение $ + pk + q = 0$ называется характеристическим уравнением для дифференциального уравнения (2**).
При решении характеристического уравнения возможны три случая:
- Если $D > 0$, то корни $k_1$ и $k_2$ — действительные различные числа. В этом случае функции $ = <e^<x>>, = <e^<x>>$ — два линейно независимых решения уравнения (2**), следовательно, общим решением будет следующая функция[<y_> = <e^<x>> + <e^<x>>.]
- Если $D = 0$, то корни $k_1=k_2$. Одно решение уравнения (2**) – это функция $ = <e^>$. Вместо второго решения (это можно проверить, подставив данную функцию в уравнение) надо взять функцию $ = x<e^>$. Эти функции будут линейно независимыми. В этом случае получим общее решение [<y_> = <e^> + x<e^>.]
- Если же $D Первый случай особой правой части – произведение многочлена и показательной функции:
$y» + py’ + qy =
left( x right) cdot <e^>$ (3**)
Частное решение в этом случае будем искать в следующем виде: [ = left( x right)<e^> cdot ,] где
$left( x right)$ — многочлен степени $n$ с неопределенными коэффициентами;
$<e^>$ — та же экспонента, что и в правой части уравнения (3**);
$$ — усиление, параметр $r$ определяется следующим образом:
- $r = 0$, если $a ne ,a ne $, т.е. $a$ не является корнем характеристического уравнения;
- $r = 1$, если $a = ,a ne $, т.е. число $a$ равно одному из корней;
- $r = 2$, если $a = = = k$, т.е. корни одинаковые и равны $a$.
Рассмотрим второй случай особой правой части:
$y» + py’ + qy = <e^>left( <
left( x right) cdot cos bx + left( x right) cdot sin bx> right)$ (4**)
Частное решение в этом случае будем искать в следующем виде: [ = <e^>left( <left( x right) cdot cos bx + left( x right) cdot sin bx> right) cdot ,] где
$left( x right),left( x right)$ — многочлены степени $l$ с неопределенными коэффициентами, а $l = max left( right)$;
- $r = 0$, если $a pm bi ne <k_> = alpha pm beta i$, т.е. числа $a pm bi$ не является корнями характеристического уравнения;
- $r = 1$, если $a pm bi = <k_> = alpha pm beta i$, т.е. числа $a pm bi$ есть корни характеристического уравнения.
Метод суперпозиции решений
Метод суперпозиции ( сложения) решений заключается в следующем: если правая часть линейного неоднородного уравнения (*) представляется в виде суммы двух функций, то и частное решение этого уравнения можно представить в виде суммы функций, то и частное решение этого уравнения можно представить в виде суммы в правой части которого стоит первое слагаемое, а второе – когда второе слагаемое.
Метод вариации постоянных
Рассмотрим общий метод решения неоднородного уравнения
[y» + py’ + qy = fleft( x right).]
Как было показано ранее, общее решение однородного уравнения [y» + py’ + qy = 0] можно представить в виде линейной комбинации двух линейно независимых решений [<y_> = + .]Будем искать общее решение неоднородного уравнения в следующем виде:
В данном случае принимается, что коэффициенты при частных решениях $$, $$ есть некоторые неизвестные функции, т.е. вместо постоянных величин будем рассматривать переменные или будем варьировать постоянные величины. Определим их, подставляя данную функцию в исходное уравнение. Для этого вычислим производную [<_> = ^prime left( x right) + <_2>left( x right) + <_1> + <_2>.] Представление (5**) достаточно общее, и поэтому можно принять, что сумма первых двух слагаемых в производной равна 0
Вычислим вторую производную [<_> = ^prime <_1> + <_2>left( x right)<_2> + <_1> + left( x right)<_2>.]
Подставим вычисленные производные в исходное уравнение
Учтём, что $,$ являются решениями однородного уравнения. Тогда для определения искомых функций получим систему условий
Полученная система является системой линейных алгебраических уравнений относительно производных искомых функций $^prime ,<_2>$. Определитель матрицы коэффициентов является определителем Вронского для функций $,$:
Т.к. функции $,$, линейно независимы, определитель Вронского не равен нулю, следовательно, система имеет единственное решение, которое можно получить, например, методом Крамера
При этом общее решение неоднородного уравнения примет вид
Отметим, что общее решение неоднородного уравнения представляется (как должно и быть) в виде суммы общего решения однородного уравнения и некоторого частного решения неоднородного.
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение
Для того, чтобы решить это уравнение надо составить характеристическое уравнение, которое получается из данного уравнения , если в нем заменить y»=k 2 , y’=k, a y=k 0 =1.
— это квадратное уравнение.
Общее решение характеристического уравнения строиться в зависимости от характера его корней.
Возможны три случая:
— дискриминант квадратного уравнения больше нуля D > 0 , уравнение имеет два действительный различных корня, k1≠ k2, и общее решение характеристического уравнения имеет вид:
— дискриминант характеристического квадратного уравнения равен нулю D= 0, уравнение имеет два действительный кратных корня, k1= k2= k, и общее решение уравнения имеет вид:
— дискриминант квадратного уравнения меньше нуля D 2 +7k+6=0.
Решим его: D=49-24=25, k1= -1, k2 = -6. Так как корни действительные и разные, то, согласно формулы , получаем общее решение:
Пример 10.9. Найти общее решение дифференциального уравнения
Решение. Составим характеристическое уравнение
Решим это уравнение: D = 36 -36 = 0, k1 = k2 =3. Характеристическое уравнение имеет два действительных кратных корня, следовательно, общее решение находим по формуле :
Пример 10.10. Найти общее решение дифференциального уравнения
Решение. Составим характеристическое уравнение
Решим его. Дискриминант квадратного уравнения меньше нуля, D=-36, уравнение имеет пару комплексно сопряженных корней , k1,2= 
(α=2, β=3) и общее решение уравнения имеет вид:
Пример 10.11. Найти частное решение дифференциального уравнения
y»-5y’+4y=0, удовлетворяющее начальным условиям у'(0)=8, у(0)=5.
Решение. Сначала найдем общее решение, для этого составим
Дискриминант этого уравнения D=1, следовательно, уравнение имеет два действительный корня, k1 = 2, k2 = 3 и общее решение уравнения имеет вид:
Чтобы найти частное решение, сначала найдем у’=2С1e 2 x +3C2e 3 x , а затем подставим в общее решение и в производную от функции-решения у начальные условия и получим систему для определения постоянных С1 и С2 .
.
Таким образом искомое частное решение имеет вид: y =7e 2 x – 2e 3 x .
Не нашли, что искали? Воспользуйтесь поиском:
🎦 Видео
Дифференциальные уравнения. 11 класс.Скачать
Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать
16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Решение задачи Коши дифференциального уравнения #maths #calculus #differentialequation #algebraСкачать
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать
13. Как решить дифференциальное уравнение первого порядка?Скачать
Однородные дифференциальные уравнения первого порядка #calculus #differentialequation #maths #Скачать
Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать
Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать
Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать
Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать
Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать
Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать
Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать
