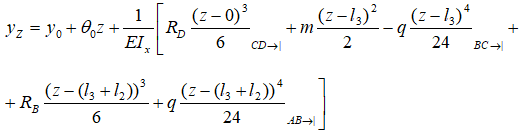Уравнение начальных параметров в функциях крылова

Метод начальных параметров (сокр. — МНП) позволяет определять прогибы и углы наклона сечений в прямых балках с постоянной жесткостью поперечного сечения EI_x.

МНП является одним из относительно простых способов расчета угловых и линейных перемещений при изгибе в балках с любым количеством силовых участков.

Пример расчета перемещений сечений балки смотрите в нашем видеоуроке:

Для применения метода начальных параметров есть ограничения: рассчитываемая балка должна быть выполнена из однородного материала, иметь прямую ось и постоянные форму и размеры поперечного сечения.

Универсальные уравнения МНП

Для балок с типичным набором нагрузок универсальные уравнения метода начальных параметров имеют вид: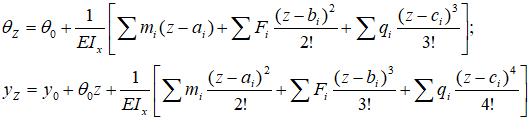

где
θ_z, y_z – соответственно угловое и линейное перемещения рассматриваемого сечения балки;
θ₀, y₀ – угол наклона и прогиб сечения балки в выбранном начале координат (НК). Это и есть начальные параметры (являются постоянными интегрирования) по которым назван сам метод. Определяются из соответствующих опорных условий;
m, F и q – все сосредоточенные моменты (пары сил), силы (включая опорные реакции) и распределенные нагрузки (в т.ч. компенсирующие) приложенные к рассматриваемой балке;
z – расстояние от выбранного начала координат до рассматриваемого сечения балки (положение сечения);
a и b – расстояния от начала координат до соответствующих моментов и сосредоточенных сил;
c – расстояние от НК до начала действия распределенной нагрузки;
E – модуль продольной упругости материала балки;
I_x — момент инерции сечения относительно оси x.

Данные уравнения МНП являются лишь шаблонами, по которым записываются уравнения для конкретных расчетных схем (пример рассмотрен ниже).

Примечания к методу

Перед записью уравнений метода начальных параметров выбирается начало координат балки.

Начало координат выбирается в крайнем левом или правом конце балки (лучше в том, который расположен на опоре).

Слагаемые в уравнениях записываются последовательно по силовым участкам от начала координат.

Знаки отдельных слагаемых в универсальных уравнениях МНП принимаются по правилу знаков для изгибающего момента, т.е. слагаемые с нагрузками, которые на рассматриваемом участке стремятся сжать верхние слои балки, записываются положительными.

Если распределенная нагрузка q действует в пределах части длины балки (обрывается, не доходя до конца), то ее действие продлевается в сторону, противоположную от начала координат, до конца балки и добавляется компенсирующая нагрузка той же интенсивности но обратного направления.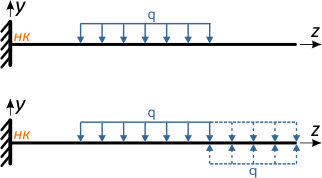

Начальные параметры универсальных уравнений МНП определяются из условий закрепления балки в опорах.
На шарнирных опорах вертикальные линейные перемещения (прогибы) равны нулю, т.е. y_A=0 и y_B=0.

В жесткой заделке отсутствуют (равны нулю) и угловые и линейные перемещения (θ_A=0, y_A=0).

Положительное значение рассчитанного прогиба y_z соответствует перемещениям сечения вверх по отношению к продольной оси балки.

Знак угла поворота θ_z зависит от выбора начала координат: при выборе НК в крайнем левом сечении балки угол θ_z будет считаться положительным при повороте сечения против хода часовой стрелки

Соответственно, если начало координат выбрано справа – положительным считается угол при повороте по часовой стрелке.

Пример составления уравнений МНП

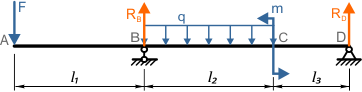
Порядок составления уравнений МНП и расчета перемещений рассмотрим на примере двухопорной балки

Выбор начала координат

Начало координат в данной расчетной схеме выбираем в самой правой точке D балки, так как она расположена на опоре, и, следовательно, прогиб в этой точке будет отсутствовать.
Ось z направляем соответственно влево.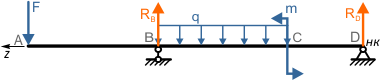

Теперь для данной балки правый торец будем считать ее началом, левый – соответственно концом.

Действия с распределенной нагрузкой

Как видно по схеме, действие распределенной нагрузки обрывается в точке B, не доходя до конца балки.

Поэтому ее действие необходимо продлить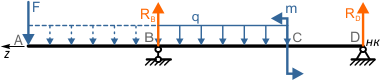

при этом схема нагружения балки изменилась. Теперь, чтобы вернуться к начальной системе нагрузок, добавляем компенсирующую распределенную нагрузку обратного направления.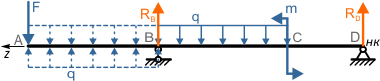

Это действие выполняется, потому что в уравнениях МНП параметр «c» учитывает только начало действия нагрузки.

Составление уравнений МНП

Универсальные уравнения МНП для заданной балки записываются последовательно по участкам со стороны начала координат.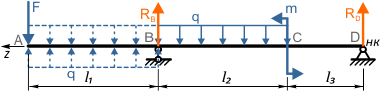

При этом желательно отделять части уравнения для каждого из участков.

Запишем уравнение угловых перемещений θ_z метода начальных параметров.
Участок CD
Мысленно закрепив балку между сечениями C и D,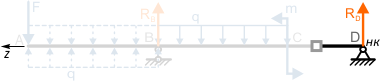

в стороне начала балки видим только опорную реакцию R_D которая по правилу знаков записывается положительной, так как сжимает верхние слои балки.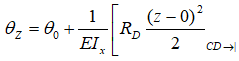

Участок BC
На этом участке, как и на всех остальных, закрепив балку в произвольном месте, смотрим в сторону НК.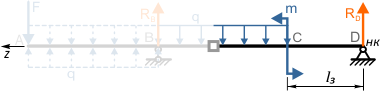

Видим момент m и распределенную нагрузку q.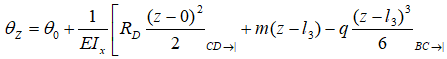

Момент положителен т.к. сжимает верхние слои балки, нагрузка q отрицательна т.к. сжимает ее нижние слои.

Заметим, что здесь мы записали сразу всю «верхнюю» распределенную нагрузку q. В данном уравнении для других участков ее записывать больше не надо.
Участок AB
При рассмотрении данного участка к уравнению добавляются реакция в опоре B и «нижняя» компенсирующая нагрузка q.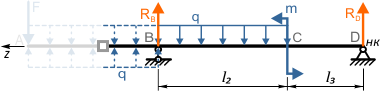

Записываем их положительными, т.к. они стремятся сжать верхние слои балки.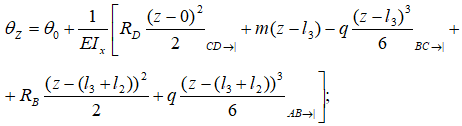

Силы и моменты, приложенные в самом конце балки, в уравнения не входят.
На вопрос «Разве сила F не влияет на перемещение сечений?» ответ следующий: В уравнениях метода начальных параметров поперечная сила и момент, приложенные к концу балки оказывают влияние на перемещения опосредованно, через опорные реакции R.

Уравнение метода начальных параметров для прогибов составляется аналогично.

Определение начальных параметров

В правой части полученных уравнений известны все параметры кроме начальных θ₀ и y₀ (переменная z задается при решении).

Прогиб и угол наклона сечения в начале координат определим из опорных условий.

Балка закреплена на двух шарнирных опорах (точки B и D), в которых прогибы всегда равны нулю.

Граничные условия метода начальных параметров: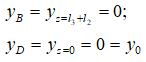

Так как точка D была принята за начало координат, то прогиб в этой точке и есть y₀, т.е. правильно выбрав НК, мы сразу определили один из двух начальных параметров.

Угловое перемещение в начале координат θ₀ рассчитаем из оставшегося (первого) опорного условия.

Для этого запишем уравнение прогибов для точки B, которое равно нулю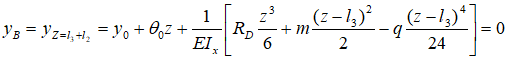

От НК до сечения B два участка, поэтому берется не все уравнение, а только его части, включающие нагрузки на соответствующих участках (CD и BC).
Из него выражаем и находим значение θ₀.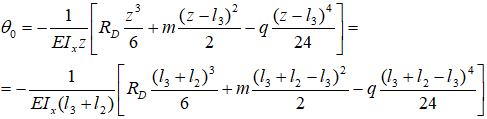

Теперь можно рассчитывать перемещения любого сечения балки.

Расчет перемещений

Для определения перемещений сечения расположенного на i-м участке от начала координат в расчете участвуют только части уравнений от НК до i-го участка включительно.

Выбирая нужное уравнение и задавая положение z сечений от начала координат определяются их угловые и линейные перемещения.

Например, для расчета угла наклона и прогиба сечения K расположенного на расстоянии z_K от НК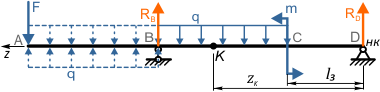

уравнения метода начальных параметров будут иметь вид: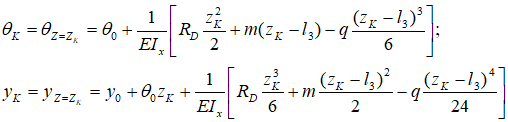

Остается только подставить значения и провести расчеты.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Понятие о расчете коротких балок, лежащих на сплошном упругом основании. метод начальных параметров

Понятие о расчете коротких балок, лежащих на сплошном упругом основании. метод начальных параметров

• Концепция расчета короткого луча, Лежащих на сплошном упругом База. Метод начального параметра Короткая балка, лежащая на твердом упругом основании(рис. 293), использовать дифференциальное уравнение(10.20)) +4 p4m=4-d». Рис 293А Дальнейшее рассмотрение ограничивается рассмотрением случая

линейных нагрузок, когда d » =0. Тогда уравнение(10.20) становится однородным Ж4■+4R4L4=0. Акадия.Н. Крылов, M=A Y1 (x) V Y2 (x)+SU3 (x) O Y b (x), (10.26) где Y Ah), T2(x), Y3(x), T4 (x) — A. N. Мы предлагаем решение этого уравнения в виде функции Крылова.: У1(х)=СП Р х соз ГХ;У2 (х)=(СП Р х ЗШ Р х+р р з х соз х);У3(Х)=-З Р х р х 81p;У4(Х)=-

У-(р х 81p Р Х—З Р х р х соз). (10.27) Между этими функциями существует Людмила Фирмаль

простая разностная зависимость, которая носит табличный характер (табл. Двенадцать.) 338T а б л и Ц А12 С Б Особенности и их значение Производная функции по отношению к X, первая, вторая и третья 1Ug(ч)=sirh soazh У2(Х)=-У (Х^H81P34-4-ж поп РЗ РЗ) -4^Г4(з) -4|^Г3(Н)-4 3″Г2(з) -4 3 4г ч(ч) Два. 3^(h) -4 3 2I4 (h)-4 3’g3 (h) — 434G2(h) 3U3 (ч)= — u8I RH81P относительной влажности≤Г2(ч)Z2U1 (х)-4 3 3G4(ч) -4 3 4G3(ч)4U4 (ч)=

у(ху резус — — — — — 5У$ч-поп РЗ) ZY3 (h)32g 2 (h)33I4 (h)-4 3g 4

(h) Непрерывно дифференцируясь по формуле X (10.26)= Людмила Фирмаль

другом конце балки. Поэтому будет описан случай, показанный на рисунке. Из условий опоры левого края балки имеем 294 0, Для определения M o и F0 мы используем условия опоры балки на ее правый край. Если правый край свободно расположен на упругом основании, то x= / M (/)=0 и 0. Например, M (/) =MOU, (/) +Ug (/) — — — — — U2 (1-a) — Ug (I-a,) — G3 (/- a2)+^ — U8 (/- a,)=0> 341(?(/)=-4≤м»у г(/)+%У1(/)-/>1G1 (/- А1)-/>2 У1 (/- А4)—±УГ(я-А2)+УГ(1-А3)=0. Когда два уравнения решаются вместе, неизвестные m y и Fo находятся. Кроме того, используя уравнение (10.31), можно найти значения M. V и V ‘ на одном из участков рассматриваемой балки. Кроме того, граничное

условие показано на рисунке в случае несущего конца балки. Двести девяносто пять Отчет Рис серийный дизель 295d Преимущество метода начальных параметров заключается в том, что, независимо от количества участков нагрузки, при определении любой константы любого способа закрепления концов балок используются два метода с двумя неизвестными. Таблица состоит из A.N.To определите особенности Крылова (В. А. см. книгу Киселева. Онти, 1936).

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение начальных параметров в функциях крылова

В этом ИДЗ мы проведём полный расчёт балки на упругом основании (рис.1), находящейся под действием произвольной системы изгибающих моментов, сосредоточенных сил и равномерно распределённых нагрузок, расположенных в вертикальной плоскости.

Это пособие предназначено для студентов, изучающих курс сопротивления материалов. Прямо из этого пособия Вы можете посчитать своё ИДЗ, даже если у Вас нет на компьютере MATLAB. Если же у Вас есть MATLAB, перейдите на эту страницу: там у Вас есть возможность вмешаться в сценарий (программу) вычислений. Здесь же выполнение ИДЗ проводится по стандартному сценарию, который обычно используется в вузах при изучении курса сопромата.

Для правильной работы с этой страницей Ваш браузер должен поддерживать сценарии Java Script. Включите их.

Данное пособие позволит вам упростить выполнение ИДЗ. Как и любой помощник, оно не избавляет вас от необходимости думать. Используя это пособие, вы получите техническую помощь, избавитесь от досадных ошибок вычислений, но понимать существо проблемы вы всё равно должны. Но не пугайтесь: если вы смогли найти эту страницу в Internet, то разобраться в выполнении этого задания сможете наверняка.

Граничные условия на каждом краю могут быть одного из трёх типов:

Выберем систему координат так, как показано на рис.2.

Начало координат O поместим на левом краю, ось Oz направим вдоль оси балки, а оси Ox и Oy − вдоль главных центральных осей инерции. Все силовые факторы считаем действующими в плоскости yOz, как показано на рис.2.

Будем использовать правило знаков плюс-плюс-плюс-плюс:

• угол поворота сечения θ есть производная от вертикального перемещения w, взятая со знаком плюс;
• изгибающий момент в сечении M есть производная от угла поворота θ, умноженного на EJ_x, взятая со знаком плюс;
• перерезывающая сила в сечении Q есть производная от изгибающего момента M, взятая со знаком плюс;
• распределённая нагрузка q есть производная от перерезывающей силы Q, взятая со знаком плюс:

В соответствии с [1] выберем положительное направление прогиба w(z) вверх, в сторону положительного направления оси Oy, а отрицательное − вниз (рис.3).

Тогда положительные значения углов поворота θ(z) будут соответствовать возрастанию прогиба w(z), а отрицательные − убыванию (рис.4).

Изгибающий момент − это вторая производная от прогиба (с точностью до положительного множителя) и первая производная от угла поворота θ(z) (опять-таки с точностью до положительного множителя); поэтому положительное значение момента M(z) соответствует увеличению угла поворота θ(z), т.е. изгибу балочки выпуклостью вниз, а отрицательный M(z) − изгибу выпуклостью вверх (рис.5).

При построении эпюр мы будем разрезать балку в данном сечении z, отбрасывать левую часть и заменять её эквивалентной системой сил и моментов. Положительное значение M(z) (выпуклостью вниз) при этом даст момент, направленный по часовой стрелке (рис.6).

Поэтому в исходных данных сосредоточенные моменты будем задавать положительными, если они направлены по часовой стрелке.

Теперь рассмотрим правило знаков для перерезывающих сил. В соответствии с (3) положительной будем считать такую силу Q(z), которая соответствует возрастанию изгибающего момента M(z) при увеличении z. Наглядно представить себе увеличение вогнутости трудно, поэтому применим другое правило для определения знака Q(z). Заменим отрезанную левую часть такой силой, которая соответствует увеличению M(z) (рис.7). Т.к. момент равен произведению силы на плечо, то положительное значение сосредоточенной силы соответствует направлению её вверх. Такая сила стремится повернуть элемент балки по часовой стрелке.

И, наконец, выведем правило знаков для распределённой нагрузки q(z). Положительная q(z) соответствует возрастанию перерезывающей силы Q(z). На рис.8 показано положительное направление q(z): вверх. Именно такое направление q(z) соответствует возрастанию Q(z).

Итак, подытожим всё вышесказанное. При задании исходных данных будем считать:

• распределённую нагрузку q положительной, если она направлена вверх;
• сосредоточенную нагрузку F положительной, если она направлена вверх;
• сосредоточенный момент M положительным, если он направлен по часовой стрелке.

При построении эпюр будем руководствоваться формулами (1-4). Считаем:

• перемещение w положительным, если оно направлено вверх;
• положительный угол поворота θ соответствует возрастанию w;
• положительный изгибающий момент M соответствует возрастанию θ;
• положительная перерезывающая сила Q соответствует возрастанию M;
• положительная распределённая нагрузка q соответствует возрастанию Q.

Краткие теоретические сведения

В соответствии с [1] выведем дифференциальное уравнение изогнутой оси балки. Это уравнение имеет вид: вторая производная от изгибающего момента EJ_xw IV (z)) равна сумме всех распределённых нагрузок в данном сечении на единицу длины. Такими нагрузками будут внешние силовые факторы и реакция упругого основания. Коэффициент жёсткости упругого основания c − это сила, с которой действует упругое основание на единицу площади нижней поверхности балки при единичном прогибе основания. Поэтому размерность c будет Н/м 3 . Если обозначить ширину нижней поверхности балки через b, то

− это сила, с которой действует упругое основание на единицу длины балки при единичном прогибе. Размерность α будет Н/м 2 . Сила реакции упругого основания на единицу длины тогда будет равна αw, и направлена в сторону, противоположную прогибу. дифференциальное уравнение изогнутой оси балки на упругом основании имеет вид:

где q(z) − обобщённая внешняя нагрузка, учитывающая все силы и моменты. Дифференциальное уравнение (6) дополняется 4 граничными условиями: по 2 на левом и правом концах, в зависимости от условий закрепления.

Решение уравнения (6) удобно записывать через функции Крылова:

Эти функции обладают свойством:

Если ввести в рассмотрение приведённую длину:

то общее решение дифференциального уравнения (6) записывается в виде:

Здесь EJ_xw₀ − прогиб в левом сечении (с точностью до множителя EJ_x), EJ_xθ₀ − угол поворота левого сечения (также с точностью до множителя EJ_x), M₀ и Q₀ − изгибающий момент и перерезывающая сила в левом сечении. Во второй строке в 1-й и 2-й суммах a_k − точка приложения сосредоточенного момента или силы; в 3-й и 4-й суммах a_k − начало приложения распределённой нагрузки, в b_k − конец. В каждой из сумм суммирование проводится по всем силовым факторам, расположенным слева от текущего сечения.

Неизвестные начальные параметры EJ_xw₀, EJ_xθ₀, M₀ и Q₀ находятся из граничных условий. Всего таких условий 4: по 2 на каждом краю балочки. Составив соответствующую систему уравнений и решив её, мы найдём эти начальные параметры.

Далее последовательное дифференцирование выражения (10) даёт угол поворота:

и перерезывающую силу:

По выражениям (10-13) можно построить эпюры.

Ввод исходных данных

В данном методическом пособии можно использовать такие нагрузки:

• сосредоточенный момент;
• сосредоточенная сила;
• равномерно распределённая нагрузка.

На концах можно задавать такие условия закрепления:

• жёсткая заделка;
• свободное опирание (шарнир);
• свободный край.

Если в вашем вузе преподаватели задают студентам другие виды нагружения (распределённые моменты, линейную нагрузку и т.п.), промежуточные опоры или другие граничные условия (например, упругая заделка), − напишите мне, и мы вместе доработаем это пособие.

Исходными данными для выполнения этого ИДЗ являются длина балочки L, граничные условия, данные по двутавровому сечению, физические характеристики материала балки и упругого основания, и нагрузка на неё: значения M, F, q и точки (интервалы) их приложения. Заметим, что здесь сечение нужно задать заранее, его данные входят в коэффициенты дифференциального уравнения (6) через множитель α (5). Задайте исходные данные в нижеприведенных областях ввода.

Измените при необходимости эти данные:

Длина балочки L (м):

Граничное условие слева:

Граничное условие справа:

Модуль упругости E (МПа):

Жёсткость упругого основания c (Н/м 3 ):

Номер профиля двутаврового сечения:

Добавьте нужные нагрузки:

Проверьте, правильно ли вы задали исходные данные. Если да, то идём дальше.

Нахождение начальных параметров

Наша балочка является статически неопределимой: неизвестные начальные параметры не могут быть найдены из уравнений статики. Они находятся из граничных условий. Для нахождения этих 4 неизвестных начальных параметров у нас есть столько же уравнений: по 2 каких-либо параметра на каждом краю балочки равны нулю − всего 4 уравнения.

В зависимости от вида граничных условий будут равны нулю:

1. в жёсткой заделке − перемещение и угол поворота;
2. при шарнирном закреплении − перемещение и изгибающий момент;
3. на свободном краю − изгибающий момент и перерезывающая сила.

Вначале найдём точки переключения аналитических выражений в формулах (10-13). Это будут: начало и конец балочки и точки приложения всех силовых факторов (для распределённой нагрузки q берём и начало, и конец приложения). Запишем также характеристики выбранного двутаврового сечения и другие необходимые для расчёта данные.

Запишем теперь систему уравнений для определения начальных параметров и решим её. Первые 2 уравнения − это граничные условия на правом конце балочки, а 3-е и 4-е уравнения − на правом конце.

Построение эпюр

Теперь, когда мы вычислили все необходимые данные для формул (10-13), строим эпюры перемещений, углов поворота, изгибающих моментов и перерезывающих сил. Вначале записываем аналитические выражения на каждом участке, а затем строим графики. Перемещения и углы поворота строим в натуральном масштабе.

Подбор сечения по условиям прочности

Найдём максимальный (по модулю) изгибающий момент M_max и сечение, в котором он достигается (опасное сечение).

находим максимальное нормальное напряжение в опасном сечении. Проверим теперь касательные напряжения. В каждом сечении они подсчитываются по формуле Журавского:

Как правило, касательные напряжения значительно меньше нормальных в одном и том же сечении, к тому же они достигаются на разных волокнах: нормальные − на крайних, а касательные − в середине сечения. Поэтому опасными является обычно нормальные напряжения.

Нарисуем распределение нормальных и касательных напряжений по сечению. Нормальные напряжения распределены линейно, а касательные − по параболе. Мы строим эпюру распределения касательных напряжений приближённо: заменяем двутавр набором прямоугольников. Вычисляем по формуле (15) напряжения в крайних волокнах тонкой вертикальной стойки и во внутренних волокнах широкой горизонтальной полки. На стойке строим параболу, а на короткой полке ограничимся прямолинейным отрезком. Рисуем сечение , распределение нормальных и касательных напряжений в опасном сечении (там, где достигается M_max), и распределение касательных напряжений в том сечении, где достигается Q_max.

Если максимальное напряжение не достигают допускаемого, можно подобрать более лёгкий двутавровый профиль из списка. А если, наоборот, превышает, выберите более тяжёлый.

Что делать дальше

Возможно, Вы захотите распечатать результаты. Если перебросить содержимое, например, в то формулы и графики исказятся, они сделаны не в виде рисунков, а в виде встроенных объектов. Поэтому лучше распечатывать страницу непосредственно из обозревателя.

💡 Видео

Изгибающий момент M и точка a его приложения	M (кНм):
	a (м):
Сосредоточенная сила Q и точка a её приложения	Q (кН):
	a (м):
Равномерно распределённая нагрузка q и интервал (a, b) её приложения.	q (кН/м):
	a (м):
	b (м):