Вы будете перенаправлены на Автор24
Видео:Собственные значения и функции в интегральных уравненияхСкачать
Гамильтониан
В классической физике функцией Гамильтона ($Hleft(overrightarrow,overrightarrow
right)$) называют полную энергию, которая выражена через импульсы и координаты частицы. Для одной частицы полная энергия равна:
где $p$ — импульс частицы, $m$ — масса частицы, $U$ — потенциальная энергия частицы.
В квантовой механике функции Гамильтона соответствует оператор. Он получится, если в выражение (1) вместо вектора импульса подставить оператор $hat
$, равный:
Введенный гамильтониан дает возможность представиться уравнение Шредингера в компактном виде:
Видео:Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать
Определение энергетического спектра системы как задача на собственные значения оператора Гамильтона
Для стационарных процессов уравнение Шредингера можно записать в виде:
где $E_n$ — собственные значения энергии, $Psi_n$ — собственные функции, являющиеся решениями уравнения (5). Каждому собственному значению энергии соответствует одно или несколько состояний системы, которые описываются одной или несколькими собственными волновыми функциями. В том случае, если одному уровню энергии соответствует несколько собственных функций или состояний, то такие уровни именуются вырожденными. Количество состояний, соответствующих одной энергии называют кратностью вырождения (статистическим весом $g(E)).$
Задача поиска собственных значений и собственных функций оператора Гамильтона самая важная среди задач на собственные значения и собственные функции операторов физических величин. Данная задача имеет название: стационарное уравнение Шредингера.
Существенный вклад в разнообразие в эту задачу вносит вид потенциальной энергии, которая входит в гамильтониан. Энергетический спектр может быть дискретным, непрерывным, а может представлять собой часть дискретных уровней, а часть иметь непрерывного спектра.
Готовые работы на аналогичную тему
Известный набор собственных состояний Гамильтона полезен для решения уравнения (4). Допустим, что в начальный момент времени система пребывает в состоянии $varphi left(overrightarrowright):$
Представим решение уравнения (5) в виде разложения в ряд по собственным функциям ($Psi_n(overrightarrow)$) оператора Гамильтона (данное разложение является всегда возможным и единственным):
где $C_n$ — постоянные коэффициенты разложения. Подставим выражение (7) в уравнение (5) получаем:
Примем во внимание то, что $Psi_n$ — собственное состояние оператора Гамильтона с собственным значением $E_n$ преобразуем выражение (8) к виду:
Равенство (9) выполняется, если:
Решением дифференциального уравнения (10) служит:
Коэффициенты $C_n$ определяют по волновой функции при $t=0 (6)$:
Из выражения (12) найдем:
Учтем, что при $T_nleft(t=0right)=1. $Следовательно, решением нестационарного уравнения Шредингера с начальным условием (6) является выражение:
Формула (14) описывает эволюцию собственного состояния оператора Гамильтона с течением времени. В нашем случае плотность вероятности не зависит от времени и $<left|Psi(overrightarrow,t)right|>^2=<left|Psi_n(overrightarrow)right|>^2$. В связи с этим собственные состояния оператора Гамильтона именуют стационарными. Постоянными во времени являются средние значения физических величин.
И так, если Гамильтониан не зависит в явном виде от времени, то полную волновую функцию ($Psileft(overrightarrow tright)$), которая характеризует состояние системы можно представить как произведение координатной части $Psileft(overrightarrow right)$ и экспоненты $e^<-fracE_nt>.$
Задание: Найдите уровни энергии дискретного спектра частицы в поле $Uleft(xright)=-alpha delta left(xright), alpha >0.$
Решение:
В качестве основы для решения задачи используем стационарное уравнение Шредингера:
Запишем оператор Гамильтона ($hat$) в явном виде в уравнении (1.1), получим:
[-frac<^2>frac<^2Psileft(xright)>-alpha delta left(xright)Psileft(xright)=EPsileft(xright)left(1.2right).]
Связанные состояния частицы в поле, указанном в условиях задачи могут быть только при условии $E [Psi^left(xright)+frac<^2>alpha delta left(xright)Psileft(xright)-frac<^2>EPsileft(xright)=0to Psi^left(xright)+frac<^2>alpha delta left(xright)Psileft(xright)-^2Psileft(xright)=0left(1.3right),]
где ведено следующее обозначение: $^2=-frac<^2>E.$ Общее решение уравнения (1.3) имеет вид:
Волновая функция должна стремится к нулю при $xto -infty .$ Следовательно, $B=0$. В области $-infty [Psi_1left(xright)=Ae^left(1.5right).]
Для области $0 [Psi_2left(xright)=De^left(1.6right).]
В соответствии с условием непрерывности волновой функции:
Можно сделать вывод о том, что $A=D.$
Найдем интеграл от уравнения Шредингера в области $0-varepsilon [Psi’left(0+varepsilon right)-Psi’left(0-varepsilon right)+frac<^2>alpha Psileft(0right)=0left(1.8right).]
Производная от $Psi$ претерпевает разрыв при $x=0$. Значит, величина $rho =frac<^2>$ — единственное значение. Из выражения $^2=-frac<^2>E$ следует, что имеется только одно состояние дискретного спектра с энергией:
Ответ: $E=-frac<m^2>- $единственное значение.
Задание: Задан оператор Гамильтона $hat=-frac<^2>frac<^2>-alpha delta left(xright). $Какой вид имеет волновая функция для частицы?
Решение:
Для установления вида волновой функции следует выражение $Psileft(xright)=Ae^left(1.5right)$, полученное в примере $1$ нормировать на единицу:
Из выражения (2.1) получаем:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 12.05.2021
Видео:Собственные значения и собственные векторы матрицы (4)Скачать
Гамильтониан. Оператор энергии.
Напомним основные постулаты квантовой механики, связанные с эрмитовыми операторами:
- Все величины, которые можно экспериментально измерить, в квантовой механике выражаются эрмитовыми операторами (матрицами).
- Результатом измерения величины, описываемой оператором, может являться только одно из собственных значений данного оператора.
- Собственные векторы эрмитовых операторов формируют базис по которому можно разложить исходный вектор состояния.
- Вектор состояния, описывающий систему, после измерения коллапсирует в один из собственных векторов оператора измеряемой величины, причем в тот, который соответствует измеренному собственному значению.
- Коэффициенты в разложении по базисным векторам исходного вектора состояния есть амплитуды вероятности при измерении обнаружить собственное значение, связанное с данным собственным вектором.
Оператор, связанный с измерением энергии, в квантовой механике называется оператором Гамильтона или Гамильтонианом. Конкретный вид матрицы Гамильтониана зависит от деталей рассматриваемой системы. Если это система с двумя состояниями типа кубита с двумя базисными векторами, то Гамильтониан имеет вид квадратной матрицы 2х2. В общем случае он может быть и бесконечномерной матрицей.
В классической механике энергия частицы складывается из кинетической ( displaystyle T) и потенциальной ( displaystyle V). Кинетическая энергия равна:
( displaystyle T = frac= frac
) где ( displaystyle p = mv) — импульс.
Квантовомеханический аналог получается простой заменой числового значения импульса на оператор:
Сам оператор импульса в квантовомеханическом случае выражается через оператор взятия производной:
Мы получили оператор Гамильтона в координатном базисе:
Его собственные векторы также бесконечномерные — это функции от координаты x. Аппроксимируя вторую производную квадратной матрицей и прибавляя дискретизированную функцию потенциала ( displaystyle V) получим конечномерную матрицу, аппроксимирующую Гамильтониан:
Все что остается — это выбрать конкретный вид функции потенциала и найти на компьютере собственные векторы и собственные значения данной матрицы.
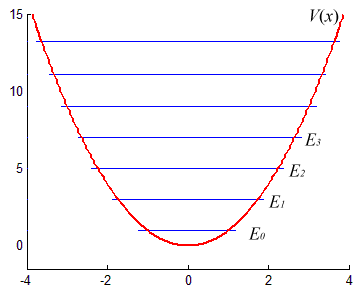
Давайте возьмем квадратичный потенциал ( displaystyle V = kx^2), отвечающий линейной силе в классическом случае (пружина, маятник). Система известна как гармонический осциллятор. Найдя собственные значения мы получим, что они отстоят друг от друга на одинаковом расстоянии, причем первый энергетический уровень не нулевой. Квантовый гармонический осциллятор, в отличие от классического, оказывается не может не совершать колебания (иметь нулевую энергию).
Мы наблюдаем эффект квантования. Измеренная энергия не может принимать любое значение, а только одно из разрешенных, дискретных.
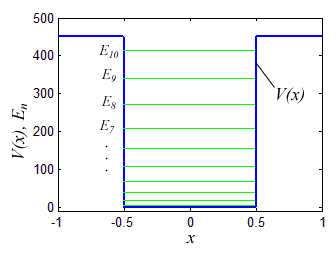
Численные величины собственных значений оператора Гамильтона зависят от вида функции потенциальной энергии. Возьмем, например, второй популярный пример — потенциал в виде прямоугольной ямы.
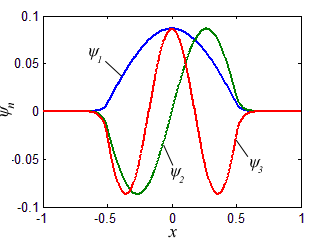
Каждому собственному значению (энергетическому уровню) соответствует собственный вектор — волновая функция в которую перейдет вектор состояния после измерения данного собственного значения (энергии). Несколько собственных функций, соответствующих нескольким первым собственным значениям Гамильтониана с прямоугольным потенциалом приведены на рисунке.
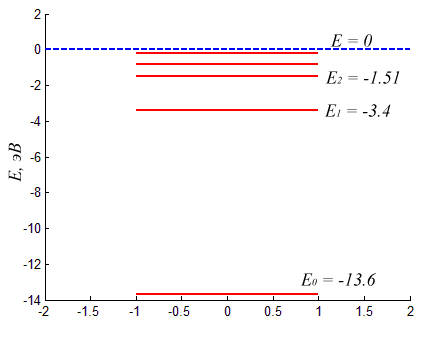
Из рисунка понятно почему квантовомеханический вектор состояния исторически получил название волновой функции. Аналогично можно найти и спектр атома водорода взяв за ( displaystyle V(x) ) кулоновский потенциал притяжения электрона и протона:
Оператор Гамильтона выделяется среди других эрмитовых операторов тем, что он является генератором эволюции во времени вектора состояния (поэтому он входит в уравнение Шредингера). В связи с этим ряд высказываний касательно времени можно сформулировать используя Гамильтониан. Так утверждение, что величина сохраняется означает ее неизменность с течением времени. На языке оператора Гамильтона данный факт преобразуется в:
Если данный эрмитов оператор коммутирует с Гамильтонианом, то физическая величина, представляемая данным оператором, сохраняется.
То есть, если ( displaystyle [A,H]=AH-HA=0), то ( displaystyle A) сохраняется.
Тривиальный случай — это закон сохранения энергии, поскольку любой оператор коммутирует сам с собой:
( displaystyle [H,H]=0 Rightarrow) энергия сохраняется.
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать
Уравнения Шредингера в операторной форме. Оператор Гамильтона
Для удобства записи и преобразования сложных уравнений часто используется символическая (операторная) форма. Так, при описании полей применяются понятия градиента, дивергенции, ротора. Сложные уравнения квантовой физики также часто принято записывать в операторной форме. Основным физическим величинам, характеризующим состояние микрочастицы, в квантовой физике соответствуют операторы.
Например, импульсу р соответствует оператор р, причем
В соответствии с этим свойством оператор импульса при воздействии на волновую функцию должен давать произведение значения импульса в данном состоянии (собственное значение импульса) на волновую функцию. Несложно убедиться, что для плоской одномерной волны |/ =Дехр[-/(оУ: — kx)] оператором импульса является символическое выражение
Действительно, подставив это выражение в формулу (34.14), получим
откуда после дифференцирования волновой функции получаем тождество р = fik.
В трехмерном случае vp = Лехр[(
i(cot — kr), и оператор импульсар выражается через оператор набла
Запишем теперь стационарное уравнение Шредингера в операторной форме. Сделаем это с помощью функции Гамильтона Я, которая по определению равна сумме кинетической энергии (выраженной через импульс) п потенциальной энергии микрочастицы:
Сформулируем аналог этого выражения в операторной форме, заменив функцию Гамильтона на оператор Гамильтона (гамильтониан) и импульс па оператор импульса:
Сравнивая два последних выражения, с учетом векторного тождества V 2 = Д получим окончательно стационарное уравнение Шредингера в операторной форме
Таким образом, мы получили выражение для оператора Гамильтона. Преобразуем теперь стационарное уравнение Шредингера (34.13) к виду
💥 Видео
Ягола А. Г. - Интегральные уравнения - Характеристические числа и собственные функции оператораСкачать
Собственные функции и собственные значения линейного гармонического осциллятораСкачать
Уравнение Шрёдингера уравнение на собственныеСкачать
Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать
ФНС. Лекция 3. Спин-орбитальное взаимодействие. Гамильтониан Латтинжера. Модель КейнаСкачать
Уравнения Гамильтона (динамика)Скачать
Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать
5_4. Уравнение ШредингераСкачать
стационарный гамильтониан | задачи по квантовой механикеСкачать
Эрмитовы операторы.Представления Шредингера и Гейзенберга.Скачать
Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать
Микролекция: Теория представленийСкачать
Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать
Авакянц Л. П. - Введение в квантовую физику - Гармонический осцилляторСкачать
(Продолжение Л. 5). Л. 6 Уравнение Шредингера в импульсном представлении.Скачать
Л. 25. Эффективные Гамильтонианы и метод инвариантов.Скачать
