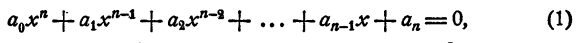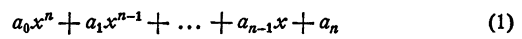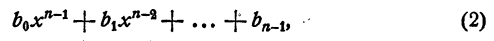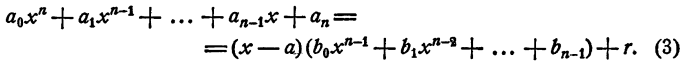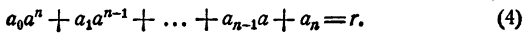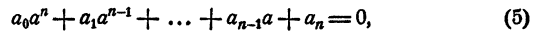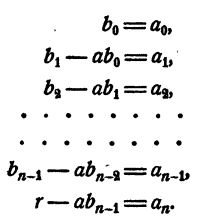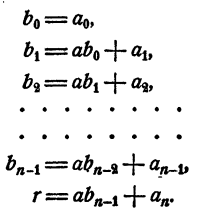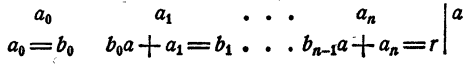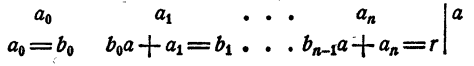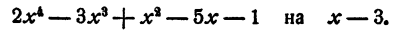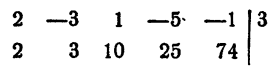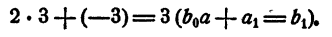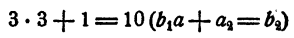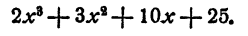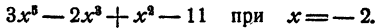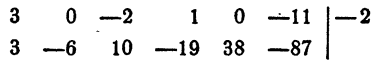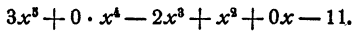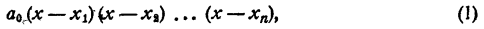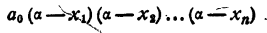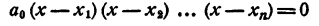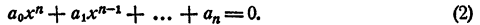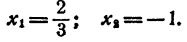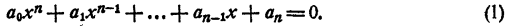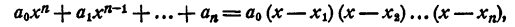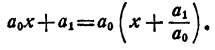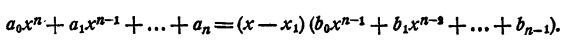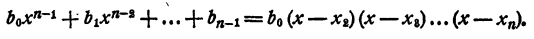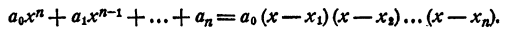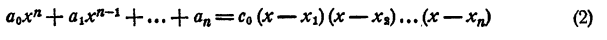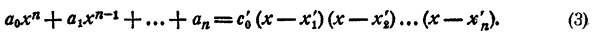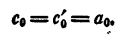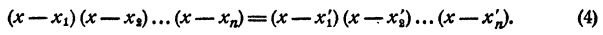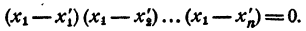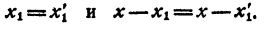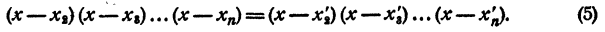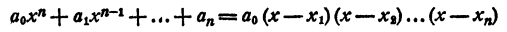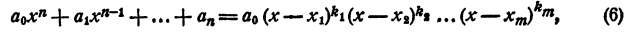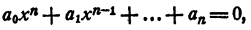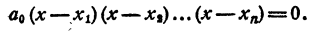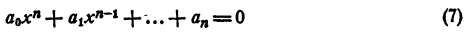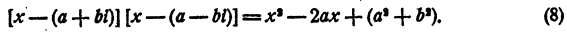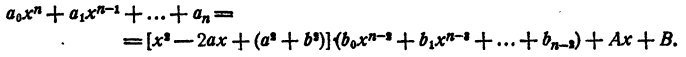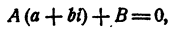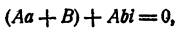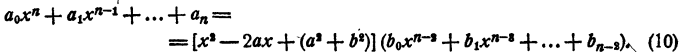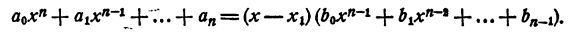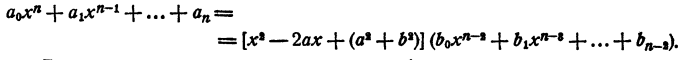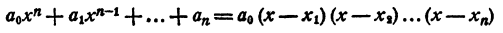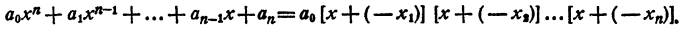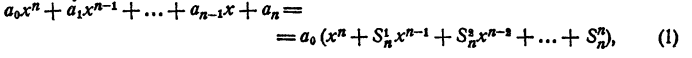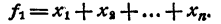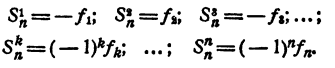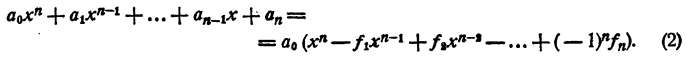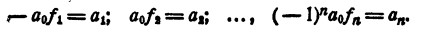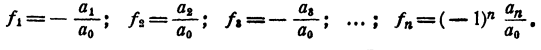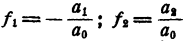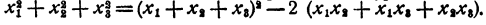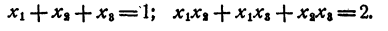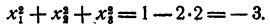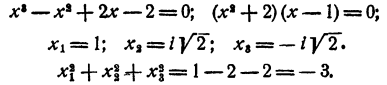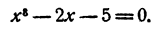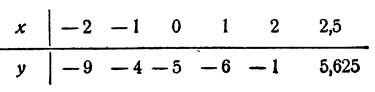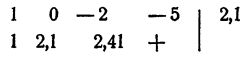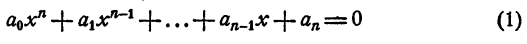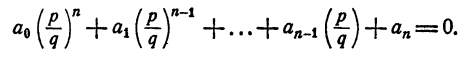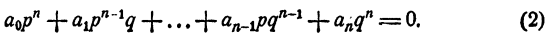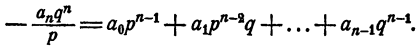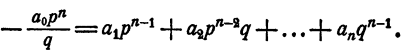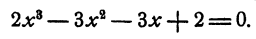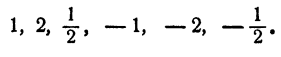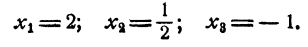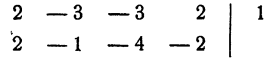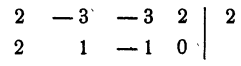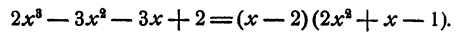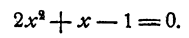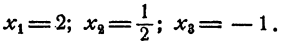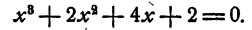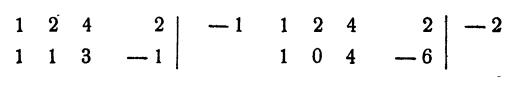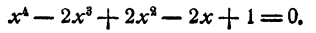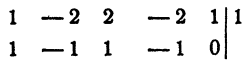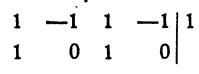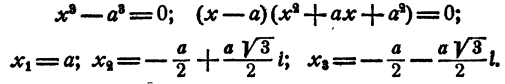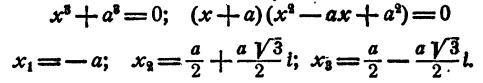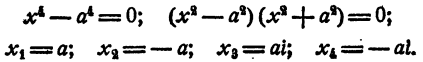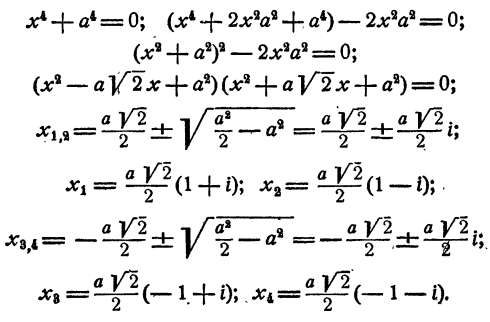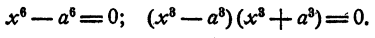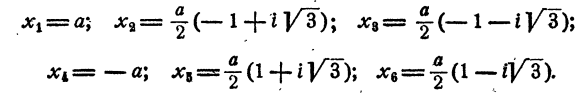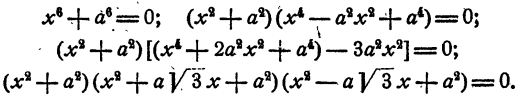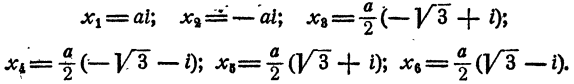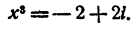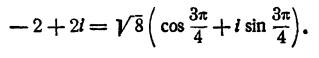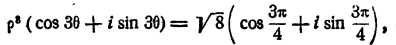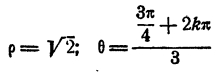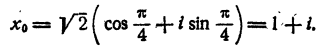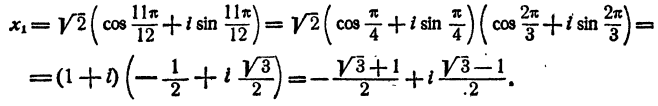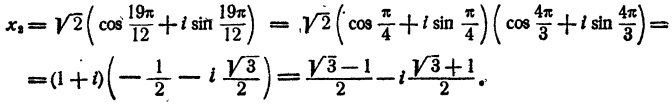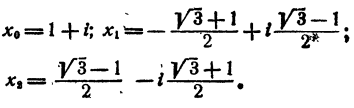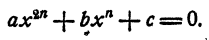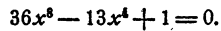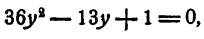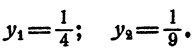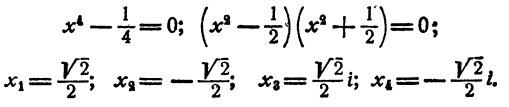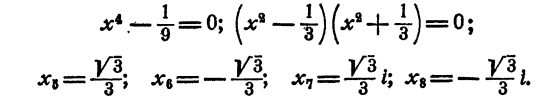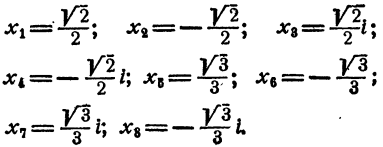Уравнение n степени имеет n решений основная теорема алгебры

Содержание:

Видео:А11 Основная теорема алгебрыСкачать

Основная теорема алгебры

Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.

Если является многочленом ненулевой степени с комплексными коэффициентами, то согласно основной теореме алгебры, у него есть хотя бы один корень . По теореме о разложении многочлена на множители получим . При этом многочлен имеет степень . Если , если , то согласно той же теореме, многочлен имеет хотя бы один корень. Обозначим его через , тогда справедливо разложение , где — многочлен степени . Значит, можно записать . Аналогично, если , то ; при , на основании той же теоремы, многочлен имеет хотя бы один корень. Обозначим его через , получим т.е. можно записать .

Продолжая процесс n раз, получаем . Тогда для многочлена можно записать следующее разложение:

здесь числа являются нулями многочлена . Эти нули могут и не быть различными.

Следствие. Многочлен n-ой степени () на множестве комплексных чисел имеет ровно n корней, включая кратные корни.

Отметим, что если комплексное число является корнем многочлена с действительными коэффициентами, то сопряженное комплексное число так же является корнем данного многочлена.

Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида , соответствующих действительным корням, и трехчленов вида , соответствующих сопряженным комплексным корням.

Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.

Задача пример №11

Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и 1+i.

Решение:

так как число 1+i является корнем многочлена, то сопряженное комплексное число 1 — i также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 15.1. Основная теорема алгебры - 1Скачать

Уравнения высших степеней в математике с примерами решения и образцами выполнения

Уравнение n-й степени с одним неизвестным:

Определение:

Уравнением n-й степени с одним неизвестным х называется уравнение

где 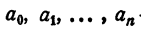— любые комплексные числа, а₀ ≠ 0, n— натуральное.

Изучение уравнения (1) в общем виде выходит за рамки школьного курса алгебры. В этой главе рассматриваются лишь некоторые свойства уравнения (1) и, кроме того, изучаются некоторые его частные виды.

Видео:24. Основная теорема алгебры. Первое доказательствоСкачать

Деление многочлена относительно х на х—а

Теорема:

Остаток от деления многочлена относительно х на двучлен х — а равен значению этого многочлена при х, равном а.

Доказательство:

Разделим многочлен n-й степени

на двучлен х — а. Как известно, частным (неполным) в этом случае будет многочлен n— 1 степени

а остатком — некоторое число r. Так как делимое равно делителю, умноженному на частное, плюс остаток, то

Равенство (3) есть тождество, оно справедливо при любых значениях х. В частности, оно справедливо и при х = а. При х = а. первое слагаемое правой части равенства (3) обращается в нуль, а потому

Следствие:

Для того чтобы многочлен относительно х делился на двучлен х — а, необходимо и достаточно, чтобы число а было корнем этого многочлена, т. е. чтобы при х = а многочлен обращался в нуль.

Доказательство:

Необходимость:

Пусть многочлен (1) делится на х — а, т. е. остаток r равен нулю. Тогда на основании равенства (4)

т. е. а — корень многочлена (1).

Достаточность:

Пусть а — корень многочлена (1), т. е. имеет место равенство (5). Тогда на основании равенства (4) r = 0, т. е. многочлен (1) делится на двучлен х — а.

Рассмотрим вновь тождество (3). Если в правой части его раскрыть скобки и сделать приведение подобных членов, в результате должен получиться тот же многочлен, что и в левой части. На этом основании, приравнивая коэффициенты при одинаковых степенях х, получаем

Перепишем эти равенства так:

Полученные равенства показывают, что коэффициенты частного и остаток, т. е. , удобно вычислять последовательно одно за другим. Эти вычисления обычно располагают следующим образом:

Пример:

Решение:

Первый коэффициент 2 второй строки просто сносится (b₀ = а₀). Второй коэффициент 3 получен так:

Третий коэффициент 10 получен так:

и т. д. Неполное частное равно

Пример:

Найти значение многочлена

Решение:

Искомое значение многочлена равно остатку от деления многочлена на x + 2

В двух местах первой строки потребовалось вписать 0. Объясняется это тем, что делимое имеет следующий вид:

Обычно члены, коэффициенты которых равны нулю, пропускаются. Здесь их пропускать нельзя.

Составление уравнения n-й степени по его корням

Теорема:

Каковы бы ни были числа можно составить уравнение n-й степени, корнями которого будут эти числа и только они. Доказательство. Составим произведение

где a₀ — любое число, отличное от нуля. При x = x₁ двучлен x — x₁ обращается в нуль, значит, при этом значении х обращается в нуль и произведение (1). При х = х₂ обращается в нуль двучлен х — x₂, и опять произведение (1) обращается в нуль. То же самое происходит при х =x₃; х = хₙ.

Пусть теперь х = а, где a — число, отличное от x₁ x₂ , …., хₙ . Ни одна из разностей а— x₁ а— x₂ ,…..о— хₙ „ не равна нулю. Число а₀ тоже отлично от нуля. Значит, и произведение

отлично от нуля.

Таким образом, уравнение

имеет корнями x₁ x₂ , …., хₙ и только эти числа.

Раскрыв скобки и выполнив приведение подобных членов, получим в левой части уравнения многочлен n-й степени относительно х, т. е.

Корнями уравнения (2) являются числа x₁ x₂ , …., хₙ и только эти числа.

Возможно, что корни x₁ x₂ , …., хₙ уравнения (2) не все различны между собой. В этих случаях говорят, что уравнение (2) имеет кратные корни. Так, например, если x₁ = x₂ и отлично от других корней уравнения (2), число является корнем второй кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (x — x₁ )³ и не делится на (х — x₁)³. Если x₁ = x₂ = x₃ и отлично от других корней уравнения (2), число x₁ является корнем третьей кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (х — x₁ )³ и не делится на (х— x₁ )⁴.

Вообще корнем кратности k уравнения (2) называется такое число а, что левая часть уравнения (2) делится на (х — а)ᵏ и не делится на

Пример:

Составить уравнение второй степени, корни которого

Решение:

. Положим а₀ = 3. Имеем

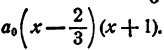
Пример:

Составить уравнение второй степени, корни которого x₁ = 1; х₂ =i.

Решение:

Положим

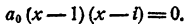
Пример:

Составить уравнение четвертой степени, корни которого i; —i; 1+i; 1-i

Решение:

Пример:

Составить уравнение третьей степени, корни которого x₁ = 1; х₂ = 1; х₃ = — 1.

Решение:

. Положим а₀ = 1.

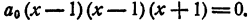
Число единица является здесь корнем второй кратности,

Видео:25. Основная теорема алгебры. Второе доказательствоСкачать

Основная теорема алгебры и некоторые следствия из нее

Мы видели, что, выбрав произвольные п комплексных чисел, можно составить уравнение п-й степени, корнями которого будут выбранные числа. Коэффициенты этого уравнения могут при -этом оказаться как вещественными, так и мнимыми. Возникает следующий весьма важный вопрос.

Дано уравнение n-й степени с комплексными коэффициентами

Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем этого уравнения?

В свое время мы видели, что среди целых чисел нет числа, являющегося корнем уравнения 2х— 3 = 0 с целыми коэффициентами. Среди положительных чисел нет числа, являющегося корнем уравнения x+ 1 = 0 с положительными коэффициентами.

Среди рациональных чисел нет числа, являющегося корнем уравнения x² — 2 = 0 с рациональными коэффициентами. Среди действительных чисел нет числа, являющегося корнем уравнения x²+ 1 = 0 с действительными коэффициентами.

Понятно поэтому, сколь важное значение имеет поставленный вопрос. Ответ на него дает основная теорема алгебры.

Всякое уравнение n-й степени с любыми комплексными коэффициентами имеет комплексный корень.

Доказательство этой теоремы выходит за рамки школьной программы.

Теорема:

Всякий многочлен n-й степени с любыми комплексными коэффициентами может быть представлен и притом единственным образом в виде произведения п двучленов первой степени, т. е.

где a ≠ 0, n ≥ 1. (Два таких разложения, отличающиеся только порядком расположения множителей, не считаются различными.)

Доказательство:

Доказательство разбивается на две части. В первой части доказывается возможность представления многочлена n-й степени в виде произведения п двучленов первой степени, во второй—единственность такого представления.

Для n = 1 теорема верна, так как

Предположим, что теорема справедлива для многочленов степени n—1.

Согласно основной теореме алгебры многочлен 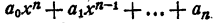имеет по крайней мере один корень x₁ и, следовательно, делится на х — х₁ т. е.

Для многочлена 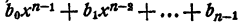теорема справедлива. Значит,

Допустим, что имеется два таких разложения:

Так как коэффициенты при хⁿ в правой и левой частях равенств (2) и (3) должны быть равны, то

Приравниваем правые части равенств (2) и (3). После сокращения на а₀ имеем

Методом математической индукции докажем, что правая и левая части равенства (4) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке.

Для n= 1 утверждение, очевидно, справедливо.

Пусть утверждение справедливо для произведений, состоящих из n—1 множителей. Докажем, что утверждение справедливо и для произведений, состоящих из n множителей.

Левая часть равенства (4) при x = x₁ обращается в нуль. Значит, при x = x₁ обращается в нуль и правая часть этого равенства, т. е.

Произведение равно нулю. Значит, хоть один из сомножителей равен нулю. Допустим, что 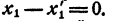В случае необходимости мы можем изменить нумерацию сомножителей так, чтобы первым был множитель, равный нулю. Тогда

Сократим равенство (4) на х— x₁ получим

По допущению правая и левая части равенства (5) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке. Приписав в каждую часть равенства (5) по одинаковому множителю х— x₁ получим, что правая и левая части равенства (4) состоят из соответственно равных сомножителей.

Теорема доказана полностью.

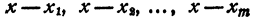
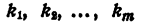
некоторые из сомножителей правой части могут быть одинаковы. Обозначив различные из них, а буквами кратность их вхождения, получим

где 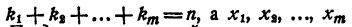все различны между собой

Представление левой части уравнения в виде (6) называется представлением левой части уравнения в канонической форме.

Теорема:

Всякое уравнение п-й степени с любыми комплексными коэффициентами имеет ровно п корней, среди которых могут быть и равные друг другу.

Доказательство:

где a₀ ≠ 0, n ≥ 0 Как доказано, левая часть может быть представлена в виде произведения n множителей первой степени. Таким образом, имеем

При x=x₁; х = х₂; х=хₙ левая часть уравнения превращается в нуль и, следовательно, х₁, х₂, …,xₙ— корни уравнения. Покажем, что никакое число а, отличное от х₁ х₂,…..хₙ, не может быть корнем этого уравнения.

Действительно, произведение а₀ (а — x₁) (а — х ₂ ,)… (а — x ₙ )не равно нулю, так как ни один из множителей его не равен нулю. Таким образом, корнями рассматриваемого уравнения являются числа x₁; х ₂ ;…; x ₙ и других корней нет.

Следствие:

Уравнение n-й степени имеет n корней, если каждый корень считать столько раз, какова его кратность.

Теорема:

Если уравнение n-й степени имеет действительные коэффициенты и мнимое число а + bi является корнем этого уравнения, то и сопряженное число а — bi является также корнем этого уравнения.

Доказательство:

Пусть мнимое число а + bi является корнем уравнения

с действительными коэффициентами. Требуется доказать, что сопряженное число а — bi также является корнем уравнения (7). Составим многочлен

Этот многочлен имеет действительные коэффициенты. Разделим левую часть уравнения (7) на многочлен (8). В частном получим многочлен n— 2 степени с действительными коэффициентами, в остатке многочлен степени не выше первой и тоже с действительными коэффициентами.

Так как делимое равно делителю, умноженному на частное плюс остаток, то

Положим в этом равенстве х = а + bi . Получим

так как и левая часть равенства и трехчлен 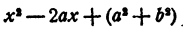при х = а + bi обращаются в нуль. Имеем

Так как b ≠ 0, то A = 0. Из первого уравнения системы (9) имеем В = 0. Выходит, что остаток Ах + В равен нулю, т. е.

При х = а — bi первый сомножитель правой части равенства (10) превращается в нуль, значит, и левая часть равенства тоже обращается в нуль. Значит, число а — bi является корнем уравнения (7).

Теорема:

Всякий многочлен n-й степени с действительными коэффициентами может быть представлен в виде произведения многочленов первой или второй степени с действительными коэффициентами.

Доказательство этой теоремы проводится методом математической индукции. Теорема, очевидно, справедлива для многочленов первой и второй степени. При этом многочлен второй степени либо имеет действительные корни и тогда разлагается на множители первой степени с действительными коэффициентами, либо он имеет два мнимых сопряженных корня, и тогда он на множители с действительными коэффициентами не разлагается.

Допустим, что теорема справедлива для многочленов n— 2 степени и многочленов n—1 степени. Докажем, что тогда она справедлива и для многочленов n-й степени.

Пусть 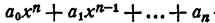— многочлен n-й степени с действительными коэффициентами.

Если этот многочлен имеет действительный корень x₁ то он представляется в виде произведения многочлена первой степени на многочлен n—1 степени с действительными коэффициентами, т. е.

Если же многочлен действительных корней не имеет, то он имеет мнимый корень а + bi и сопряженный с ним корень а — bi. В этом случае многочлен представляется в виде произведения трехчлена второй степени на многочлен n— 2 степени с действительными коэффициентами, т. е.

Так как теорема для многочленов п—1 степени и многочленов n— 2 степени справедлива, то она справедлива и для многочленов степени n.

Видео:Теорема БезуСкачать

Теорема Виета

легко получить теорему Виета для уравнений любой степени. Перепишем это равенство так:

К правой части этого равенства применим правило умножения двучленов, первые члены которых одинаковы (см. гл. VIII, § 5). Получаем

где 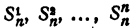имеют тот же смысл, что и в гл. VIII. Обозначим знаком f₁ сумму корней уравнения (1), т. е.

Знаком f₂ обозначим сумму всевозможных произведений корней, взятых по два. Подобный же смысл имеют знаки f₃, f₄, …, f ₙ . Тогда

Равенство (1) теперь можно переписать так:

Приравнивая коэффициенты при одинаковых степенях х в правой и левой частях равенства (2), получим

Последние равенства и выражают теорему Виета для уравнения любой степени. При n= 2, т. е. для уравнения 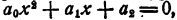получаем известный результат:

Пример:

Не решая уравнения 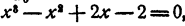, определить сумму квадратов его корней.

Решение:

Пусть х₁ x₂, х₃, — корни данного уравнения. Рассмотрим равенство

По теореме Виета

Полученный результат означает, что среди чисел х₁ x₂, х₃, имеются мнимые, иначе сумма квадратов их не могла бы быть отрицательной.

Предложенное уравнение нетрудно решить и подсчитать сумму квадратов корней непосредственно:

Видео:Аржанцев И. В. - Алгебра. Часть 1 - Основная теорема алгебрыСкачать

О решении уравнений высших степеней

Прежде всего возникает такой вопрос: можно ли для уравнений любой степени составить формулы для выражения корней уравнения через его коэффициенты, подобно известной формуле для квадратного уравнения? Оказывается, что это можно сделать для уравнений 3-й и 4-й степени, при этом формулы эти содержат столь сложные радикалы, что на практике ими предпочитают не пользоваться.

Что же касается уравнений выше 4-й степени, то доказано, что для них при помощи радикалов такие формулы составить нельзя.

В математике разработан ряд способов, дающих возможность вычислить любой корень любого уравнения с любой точностью. Один из таких способов разработан великим русским математиком, творцом неевклидовой геометрии Н. И. Лобачевским.

Ограничимся рассмотрением графического способа. Этот способ может применяться для вычисления действительных корней уравнений с действительными коэффициентами.

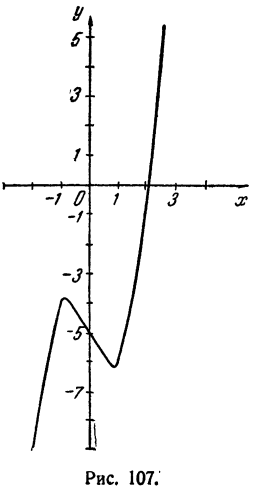
Пример:

Вычислить вещественные корни уравнения

Решение:

Построим график функции у = х³ — 2х— 5 (рис. 107). Имеем

Нетрудно видеть, что при x > 2,5 первое слагаемое х³ будет столь большим сравнительно с остальными, что у будет положительным числом.

По мере продвижения направо от х = 2,5 график будет подниматься кверху и, следовательно, больше пересекать ось Ох не будет.

Точно так же при х

Это означает, что точка 2,1 лежит правее корня, так как соответствующая ордината положительна (см. график).

Таким образом, 2 Вычисление рациональных корней уравнений с целыми коэффициентами

Теорема:

Для того чтобы несократимая дробь 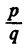была корнем уравнения

с целыми коэффициентами, необходимо, чтобы р было делителем свободного члена аₙ, a q было делителем старшего коэффициента а₀.

Доказательство:

Пусть 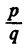—корень уравнения (1), т. е. имеет место тождество

Умножим обе части тождества на qⁿ, получим

Из тождества (2) имеем

Правая часть равенства — целое число. Значит, 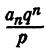целое.

По условию, дробь 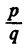несократима, значит, ни одно простое число, входящее в р, в число q не входит. По этой причине ни одно простое число, входящее в р, не может входить и в qⁿ. Выходит, что аₙ делится на р.

Из тождества (2) имеем

Так как ни одно простое число, входящее в q, не входит в р, число 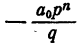может быть целым только тогда, когда а₀ делится на q.

Следствие:

Если уравнение имеет целые коэффициенты и старший из них равен единице, то рациональными корнями такого уравнения могут быть только целые числа.

Действительно, а₀ = 1, a q — делитель а₀ . Значит, q = ± 1, а тогда 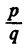целое.

Следствие:

Целые корни уравнения с целыми коэффициент тами являются делителями свободного члена.

Пример:

Вычислить рациональные корни уравнения

Решение:

Свободный член равен 2. Поэтому для р возможны только следующие значения: 1, —1, 2 и —2.

Старший коэффициент равен 2. Поэтому для q возможны только следующие значения: 1, —1, 2, —2.

Составляя всевозможными способами несократимые дроби 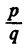найдем, что рациональные корни данного уравнения, если они имеются, содержатся среди следующих чисел:

Подстановкой в уравнение легко выяснить, что из этих шести

чисел удовлетворяют уравнению 2, 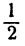,— 1.

Таким образом, уравнение имеет три рациональных корня:

Для испытания, является ли данное число корнем уравнения, удобно пользоваться правилом сокращенного деления многочлена на двучлен х — а. Для данного примера эти испытания проводятся так:

1 не является корнем уравнения, так как при делении левой части уравнения на х — 1 в остатке получилось — 2.

Испытываем число 2

2 — корень уравнения. В результате деления оказалось, что

Поэтому для отыскания остальных корней данного уравнения достаточно решить уравнение

Ответ.

Пример:

Найти рациональные корни уравнения

Решение:

Старший коэффициент уравнения равен единице, поэтому рациональными корнями уравнения могут быть только целые числа.

Делители свободного члена суть: 1,2, — 1, — 2. Сразу видно,-что никакое положительное число не может быть корнем данного уравнения, так как при любом положительном значении х левая часть уравнения положительна. Остается испытать — 1 и — 2:

Ответ. Уравнение рациональных корней не имеет.

Полученный в последнем примере результат означает, что корни рассматриваемого уравнения иррациональные или мнимые.

Пример:

Решение:

Выясним прежде всего, не имеет ли уравнение рациональных корней. Испытанию подлежат два числа 1 и — 1:

x₁² = 1. Остальные корни данного уравнения являются корнями уравнения третьей степени х³ — х² + х —1=0:

x₂ = 1. Остальные корни данного уравнения являются корнями квадратного уравнения х² + 1 = 0.

Ответ. x₁ = x₂ = 1; х₃ = i; x₄= — 1.

Решение двучленных уравнений 3-й, 4-й и 6-й степени

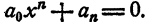
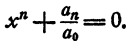
Определение. Двучленным уравнением n-й степени называется уравнение вида Очевидно, что делением на a₀ такое уравнение сводится к уравнению Если коэффициенты уравнения действительны, то двучленное уравнение можно представить в виде хⁿ — аⁿ = 0 или хⁿ + aⁿ= 0 где а — положительное число.

В этом параграфе излагается решение двучленных уравнений с действительными коэффициентами при n= 3, 4 и 6.

Уравнение имеет один действительный и два мнимых сопряженных корня.

Уравнение имеет один действительный и два мнимых сопряженных корня.

Уравнение имеет два действительных и два мнимых сопряженных корня.

Уравнение имеет две пары мнимых сопряженных корней.

Уравнение распадается на два кубических двучленных уравнения. На основании рассмотренного в п. а)

Уравнение имеет два действительных и две пары мнимых сопряженных корней

Уравнение распадается на три квадратных уравнения. Решая их, получаем

Уравнение имеет три пары мнимых сопряженных корней.

Замечание. Пользуясь извлечением корня n-й степени из комплексного числа, можно решить двучленное уравнение хⁿ = а любой степени n при любой правой части а.

Корнями уравнения хⁿ = а являются все значения корня n-й степени из а.

Пример:

Решение:

Запишем правую часть уравнения в тригонометрической форме

Пусть кубический корень из —2 + 2i равен р (cos 0 +isin 0). Тогда имеем

отсюда (§ 9 гл. IX) имеем

Для получения всех значений корня достаточно k положить равным 0, 1, 2. При k = 0 имеем

Решение трехчленных уравнений

Определение:

Трехчленным уравнением называется уравнение вида

При n= 2 уравнение является биквадратным.

Решение трехчленного уравнения подстановкой хⁿ = у сводятся к квадратному уравнению ay² + by + с = 0 и двучленному уравнению n-й степени.

Пример:

Решение:

Положим x⁴ = у. Имеем

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Основная теорема алгебрыСкачать

Основная теорема алгебры и ее следствия

Основная теорема алгебры. Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.

Следствие 1. Любой многочлен степени 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMA/sAYMQXYQYWhYbFRcq20Ms4AAACTSURBVBjTY2AgETjgEGc+pIBDRm0iigzXYgSbEVXPsmZUGebdDpd0oFKTUWQ4nbILGg0gAocmI8uYMYkwHCyAihRNR5IxZ9zA0Ah3frUKkgscLzCkwa32RJZpdGCWgEkUbUd2tSIDr4g1VALFBQzSDEwJPVBXs0JlDEEyLFIMPJINqD5tFBQUB1JAvxiDQ6cZNfAAvaobxKduFrwAAAAASUVORK5CYII=» /> с комплексными коэффициентами можно представить в виде произведения линейных двучленов:

где — корни многочлена кратности соответственно, причем . Другими словами, многочлен n-й степени имеет ровно корней, если каждый корень считать столько раз, какова его кратность.

Следствие 2. Если многочлены и , степени которых не превосходят , имеют равные значения более чем при различных значениях переменной , то эти многочлены равны: .

В самом деле, по условию многочлен имеет более, чем корней, хотя его степень меньше или равна , что противоречит следствию 1 из основной теоремы алгебры. Следовательно, это многочлен нулевой степени . Так как он имеет корни, то . Следовательно, , то есть .

Это следствие позволяет рассматривать многочлен не как формальное выражение вида (В.8), а как функцию переменной , поскольку равенство многочленов , определенное выше как равенство коэффициентов при одинаковых степенях , совпадает (в силу следствия 2) с понятием равенства двух функций при всех значениях .

Рассмотрим многочлен с действительными коэффициентами . Разложение (В. 13) для этого многочлена имеет вид

где — корни многочлена (могут быть комплексные).

Если комплексное число является корнем этого многочлена, то есть

то сопряженное число также является его корнем, т.е. . Это вытекает из равенства . Поскольку числа и не являются корнями многочлена, то он делится (без остатка) на произведение

Так как сумма и произведение сопряженных чисел являются действительными числами, то правая часть последнего равенства есть квадратный трехчлен с действительными коэффициентами. Причем, если , то дискриминант этого квадратного трехчлена отрицательный.

Следствие 3. Если комплексное (но не действительное) число — корень многочлена с действительными коэффициентами, то сопряженное число является его корнем той же кратности.

В самом деле, если — корень кратности , то для него выполняются условия (В.12)

следует, что — корень той же кратности .

Следствие 4. Всякий многочлен с действительными коэффициентами представляется в виде произведения линейных двучленов и квадратных трехчленов (с отрицательными дискриминантами):

где — действительные корни кратности , причем .

Следствие 5. Многочлен нечетной степени с действительными коэффициентами всегда имеет хотя бы один действительный корень.

Многочлен четной степени с действительными коэффициентами может не иметь действительных корней (при этом в разложении (В. 14) отсутствуют линейные двучлены ).

Пример В.14. Многочлен

а) представить в виде (В.14);

б) представить в виде (В.13).

Решение. Данный многочлен имеет двойной корень и простой корень (см. пример В.13). Поэтому его можно представить в виде

Разделим многочлен на многочлен «уголком»:

Следовательно, имеем . Это разложение имеет вид (В.14), поскольку дискриминант квадратного трехчлена отрицательный, что и требовалось в пункте «а»;

б) разложим квадратный трехчлен на линейные множители, что возможно над полем комплексных чисел:

так как уравнение имеет два комплексных корня .

Тогда разложение (В. 13) для данного многочлена принимает вид

Согласно следствию 1, многочлен имеет один двойной корень , один простой действительный корень и пару простых сопряженных корней , то есть всего 5 корней (с учетом их кратности).

🔍 Видео

Комплексные корни квадратных уравнений Основная теорема алгебрыСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Билет 15 (Корень многочлена, основная теорема алгебры, Безу, Виет, разложение и очень много боли)Скачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Теорема Виета для уравнений высших степеней. Рациональные уравнения Часть 4 из 4Скачать

Теорема Виета для многочлена 3 порядка. 10 класс.Скачать

Иллюстрация к доказательству основной теоремы алгебры (Дама с собачкой)Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Уравнение четвертой степениСкачать

Схема Горнера. 10 класс.Скачать