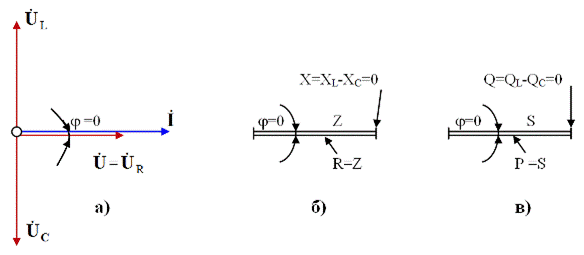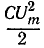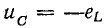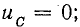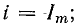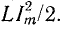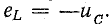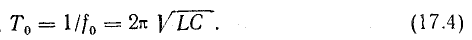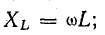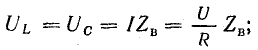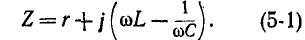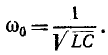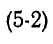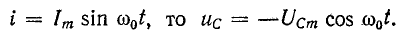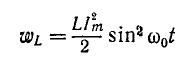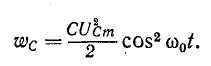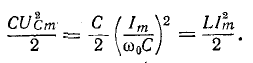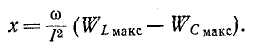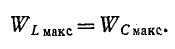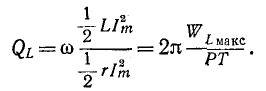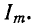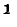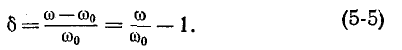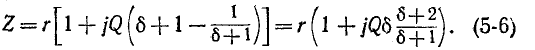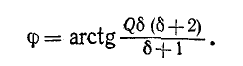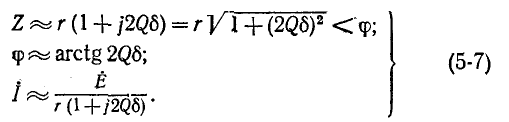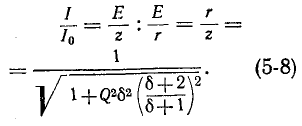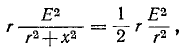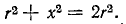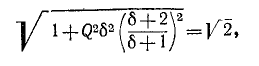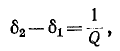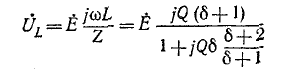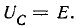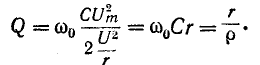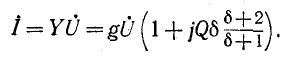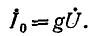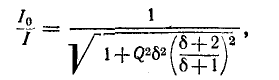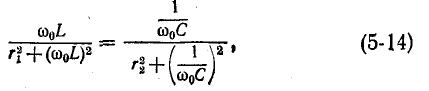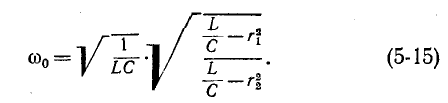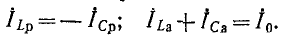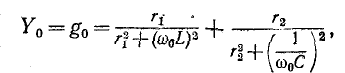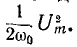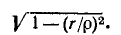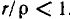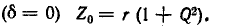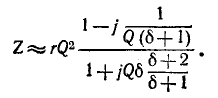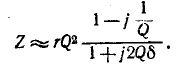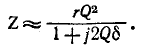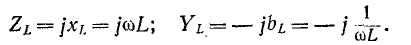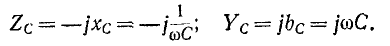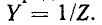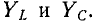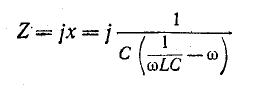Резонансом напряжений называется режим электрической цепи синусоидального тока с последовательным соединенением резистивного R, индуктивноо L и емкостного С элементов, при котором угол сдвига фаз между общим напряжением (напряжением сети) и током в цепи равен нулю.
Условием наступления резонанса напряженийявляется равенство индуктивного и емкостного сопротивлений цепи:
Электрическая цепь, питаемая синусоидальным переменным током, в которую входит конденсатор и катушка индуктивности называется колебательным контуром.
Резонанс напряжений можно получить тремя способами:
1. Изменением частоты w синусоидального тока;
2. Изменением величин индуктивности или емкости колебательного контура, при котором меняются индуктивное XL или емкостное XC сопротивление;
3. При одновременном изменении параметров w, L, C цепи колебательного контура.
Из условия резонанса напряжения (3.27) следует, что так как
то при резонансе напряжений
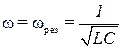
где wрез, рад/сек – резонансная частота.
Резонанс напряжений характеризуется рядом существенных особенностей:
1. Так как при резонансе напряжений угол сдвига фаз между напряжением и током равен нулю (j = yu – yi = 0), то коэффициент мощности при резонансе принимает наибольшее значение, равноеединице:
В этом случае, как видно из векторной диаграммы на рис. 3.22,а, вектор тока 
2. При резонансе напряжений векторы напряжения на индуктивном и емкостном элементах оказываются равными по величине и противоположными по фазе:
так как XLI = XCI, а в комплексной форме 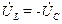
3. Напряжение на активном сопротивлении при резонансе напряжений оказывается равным напряжению сети (рис. 4.22,а) так как
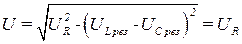
В комплексной форме 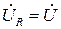
4. Отношение индуктивного или емкостного сопротивлений к активному сопротивлению цепи с R,L,C-элементами при резонансе называется добротностью колебательного контураQ
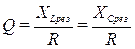
Умножив числитель и знаменатель этих дробей на ток I, получим выражения для добротности колебательного контура через отношения напряжений
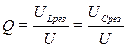
При больших значениях индуктивного XL и емкостного XC сопротивлений и малых значениях активного сопротивления R цепи (R > U:
то есть напряжение на индуктивности и конденсаторе последовательного колебательного контура при его высокой добротности в режиме резонанса напряжений могут во много раз превысить напряжение питания.
Например, если у колебательного контура последовательной цепи с
R,L,C-элементами, питаемым синусоидальным напряжением U = 220 В, R = 1 Ом, XLрез = XCрез = 1000 Ом, то напряжение на индуктивности и конденсаторе, как следует из (3.34) равно:
Поэтому при работе электротехнического оборудования, питаемого сетевым напряжением 220/380 вольт резонанс напряжений никогда не используется.
Однако в разнообразных устройствах радиотехники и электроники, где напряжение питания колебательного контура составляет микровольты
(1мкВ = 10 -6 В), резонанс напряжений широко используется, позволяя многократно усилить входной сигнал в виде синусоидального напряжения.
Рис. 3.22. Резонанс напряжений в цепи с последовательным соединением R,L,C-элементов
а) – векторная диаграмма; б) – вырожденный треугольник сопротивлений (Х = 0);
в) – вырожденный треугольник мощностей (Q = 0)
5. Так как при резонансе напряжений XL = XC (3.27), то полное сопротивление цепи принимает минимальное значение, равное активному сопротивлению:
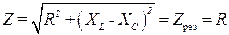
а общее реактивное сопротивление цепи становится равным нулю:
Поэтому треугольник сопротивлений при резонансе напряжений имеет вырожденный характер, как показано на рис. 3.22,б.
6. На основании закона Ома и из формулы (3.35) следует, что ток I в цепи при резонансе напряжений достигает наибольшего значения:
Отсюда следует, что ток в цепи при резонансе напряжений может оказаться значительно больше тока, который мог бы быть при отсутствии резонанса.
Это свойство позволяет обнаружить резонанс напряжений при изменении частоты w, изменении индуктивности L или емкости С. Однако резонансный ток при определенных условиях опасен – он может, достигнув чрезмерно большой величины, привести к перегреву элементов цепи и выходу их из строя.
7. Активная мощность при резонансе напряжений имеет наибольшее значение, так как связана с квадратом тока
8. Общая реактивная мощность Q при резонансе напряжений равна нулю:
так как UL = UC . Поэтому треугольник мощностей при резонансе имеет вырожденный характер, как показано на рис. 3.22,в.
то есть эти мощности могут во много раз превысить потребляемую полную мощность S. При этом полная мощность S при резонансе целиком выделяется на резистивном элементе R, в виде активной мощности Р.
Физически это объясняется тем, что при резонансе напряжений происходит периодический обмен энергии магнитного поля в индуктивном элементе и энергии электрического поля в конденсаторе. При этом интенсивность этого обмена, как величины реактивных мощностей QL и QC , в сравнении с потребляемой активной мощностью Р
определяется соотношениями реактивных и активного сопротивления цепи, как и для напряжений UL, UC и U, то есть добротностью Q колебательного контура цепи (см. п.4).
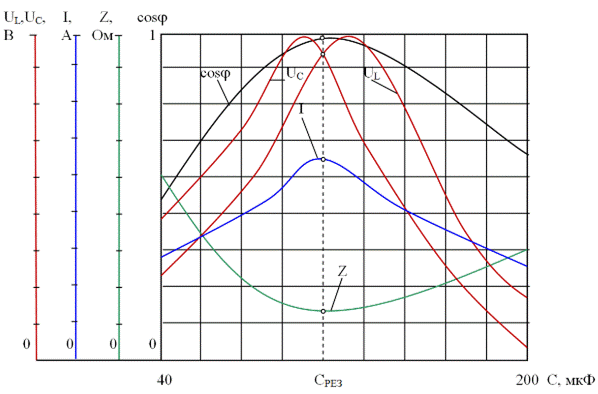
Кривые, выражающие зависимость полного тока I, сопротивления цепи Z, напряжения на индуктивности UL и конденсаторе UС , коэффициента мощности cosj от емкости батареи конденсатора С, называются резонансными кривыми.
На рис. 3.23 приведены резонансные кривые (UL, UС, I, Z, cosj) = f(C), построенные в общем виде при U = const и w = 2pf = const.
Рис. 3.23. Резонансные кривые UL , UС , I , Z, cosj в зависимости от емкости С
при последовательном соединении катушки индуктивности и батареи конденсаторов
Анализ этих зависимостей показывает, что при увеличении емкости С батареи конденсаторов полное сопротивление цепи Z сначала уменьшается, достигает минимума в режиме резонанса и становится равным активному сопротивлению R , а затем снова возрастает с увеличением емкости. Соответственно изменению Z меняется полный ток цепи (по закону Ома I обратно пропорционален Z): с ростом емкости конденсаторов ток I вначале увеличивается, достигает максимума в режиме резонанса, а затем вновь уменьшается.
Коэффициент мощности cosj изменяется с изменением емкости С в том же порядке: сначала с увеличением емкости С коэффициент мощности возрастает, достигая максимума равного единице в режиме резонанса, а затем уменьшается, в пределе стремясь к нулю.
Напряжения на индуктивности и конденсаторах имеют максимумы вблизи режима резонанса и становятся равными друг другу в этом режиме. Следует отметить, что достигаемые величины напряжений на конденсаторах и катушке индуктивности в режиме резонанса напряжений и вблизи него могут во много раз превышать входное напряжение приложенное ко всей цепи (см. п. 4).
С точки зрения электробезопасности и безаварийного режима работы, это следует учитывать при проведении исследования резонанса напряжения на стенде, задавая величину напряжения питания цепи U в достаточно низких пределах (U = 20 ¸ 25 В).
Таким образом, резонансные кривые позволяют установить минимальное полное сопротивление и наибольший ток в цепи при максимуме коэффициента мощности, равном единице, когда в цепи с последовательным соединением катушки индуктивности и батареи конденсаторов возникает резонанс напряжений.
Выводы:
1. Резонанс напряжений в промышленных электротехнических установках, питаемых синусоидальным сетевым напряжением 220/380 В – нежелательное и опасное явление, так как может вызвать аварийную ситуацию при возможном перенапряжении на отдельных участках цепи, привести к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов и опасно для обслуживающего персонала.
2. В то же время, резонанс напряжений широко используется в радиотехнике, в автоматике и электронике для настройки колебательных контуров в резонанс на определенную частоту, а также в различного рода приборах и устройствах, основанных на резонансном явлении.
Содержание работы
Лабораторная работа 2б делится на четыре части:
1. Подготовительная часть.
2. Измерительная часть (проведение опытов и снятие показаний приборов).
3. Расчетная часть (определение расчетных величин по формулам).
4. Оформительская часть (построение векторных диаграмм).
Примечание
Электромонтажные работы по исследованию резонанса напряжений в цепи с последовательным соединением R,L,C-элементов на модернизированном лабораторном стенде ЭВ-4 не проводятся, в отличие от работ на старых стендах (см. в [2] – Работа 2б, п.2. Электромонтажная часть).
1. Подготовительная часть
Подготовка к проведению лабораторной работы включает:
1. Изучение теоретической части настоящего пособия и литературы [1,2,3,4], относящихся к теме данной работы.
2. Предварительное оформление лабораторной работы в соответствии с существующими требованиями [2,3].
В результате предварительного оформления лабораторной работы №2б в рабочей тетради или журнале (на листах формата А4 с компьютерной распечаткой) студентом должен быть заполнен титульный лист, в работе должны быть указаны название работы и ее цель, приведены основные сведения по работе, взятые из раздела выше и формулы, необходимые для вычисления расчетных величин, представлены принципиальные и эквивалентные схемы замещения, заготовлены таблицы, соответственно числу опытов в работе.
Кроме этого, должно быть оставлено свободное место для построения векторных диаграмм.
2. Измерительная часть
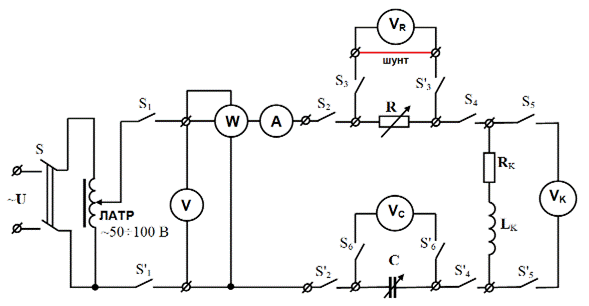
Необходимые измерения параметров исследуемой цепи однофазного тока с последовательным соединением электроприемников при резонансе напряжений проводятся с помощью принципиальной схемы (рис. 3.24). Данная схема соответствует панели модернизированног стенда ЭВ-4 [4] с аналогичной мнемосхемой и цифровыми измерительными приборами (см. фото на рис. 3.26).
Для более заметного вида резонансных кривых в последовательной цепи электроприемников резистор R отсутствует (на принципиальной схеме рис. 3.23 он зашунтирован).
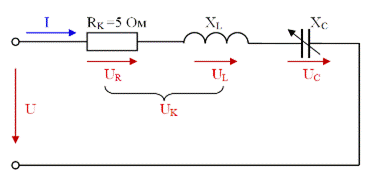
Этой схеме соответствует схема замещения с последовательно соединенными катушкой индуктивности и батареей конденсаторов, показанная на рис. 3.25.
3.24 Принципиальная схема цепи с последовательно соединенными
катушкой индуктивности и батареей конденсаторов
для исследования резонанса напряжений
3.25 Схема замещения цепи с последовательно соединенными
катушкой индуктивности и батареей конденсаторов
для исследования резонанса напряжений
1. Перед подачей питания к исследуемой цепи на панели стенда с мнемосхемой и цифровыми измерительными приборами (рис. 3.26) перевести все выключатели (S1 ÷ S6, S’1 ÷ S’6), расположенные на этой панели, в нижнее положение (состояние – «откл»).
Рис. 3.26. Паналь стенда с цифровыми измерительными приборами и
мнемосхемой для проведения лабораторой работы 2б «Резонанс напряжений
в однофазной цепи с активно-реактивными элементами»
2. На панели стенда из последовательной цепи R,L,C-элементов исключить резистор R, зашунтировав его с помощью электромонтажного провода (красный провод-шунт на принципиальной схеме рис. 3.24) вставив его концы в гнезда по бокам вольтметра VR.
3. Установить начальную общую емкость конденсаторов С = 40 мкФ нажатием соответствующих черных кнопок выключателей рядом с подключаемыми конденсаторами на панели №4 стенда с мнемосхемой батареи конденсаторов (см. рис. 3.28).
4. Подключить лабораторный автотрансформатор (ЛАТР), установленный на горизонтальной панели блока питания (рис. 3.27) к сетевому напряжению (
220 В), нажав черные кнопки «вкл» выключателей. При этом загораются две сигнальные лампы «сеть». После этого нужнообязательноповернуть ручку регулятора ЛАТРАа против часовой стрелки до упора, тем самым, снизив напряжение на его выходе до нуля.
Рис. 3.27. Панель блока питания лабораторного стенда
Рис. 3.28. Панель №4 стенда с мнемосхемами батареи конденсаторов
и катушки индуктивности
5. Подать регулируемое напряжение от ЛАТРа ко входу исследуемой цепи и подключить цифровые измерительные приборы, установив на панели стенда с мнемосхемой кнопки всех выключателей (S1 ÷ S6, S’1 ÷ S’6) в положение «вкл». При этом должны засветиться зеленые цифры на электроизмерительных приборах.
6. Плавным поворотом по часовой стрелке ручки регулятора ЛАТРа (рис. 3.27) установить напряжение U на входе цепи порядка 20 ÷ 25 В, контролируя его цифровым вольтметром V (прибор ЩП02М, установленный слева на панели стенда – рис. 4.26). Следует поддерживать установленное напряжение постоянным во всех опытах с помощью ЛАТРа.
7. В процессе исследования цепи с последовательно соединенными катушкой индуктивности и батареей конденсаторов провести 9 опытов с различной емкостью батареи конденсаторов (величины емкостей для каждого опыта указаны в табл. 3.5) нажатием соответствующих кнопок выключателей на панели №4 стенда (рис. 3.28), постепенно увеличивая емкость с 40 мкФ до 200 мкФ. Перед подключением дополнительных конденсаторов в каждом опыте нужно обязательно отключить исследуемую цепь от источника питания (выхода ЛАТРа), переведя выключатели (S1, S’1) в нижнее положение «откл», а перед проведением замеров вновь подключить к напряжению питания цепь с помощью тех же выключателей.
8. Во всех опытах измерить входное напряжение U, потребляемую активную мощность Р и протекающий по цепи ток I, соответственно цифровыми измерительными приборами: вольтметром V, ваттметром W и амперметром А (см. принципиальную схему на рис. 3.24 и панель стенда на рис. 3.26).
9. Напряжение на батарее конденсаторов UС и напряжение на катушке индуктивности UК с параметрами RK, LK измерить цифровыми вольтметрами, соответственно VC и VK, установленными на панели стенда (см. рис. 3.26).
10. Полученные результаты измерений каждого опыта занести в таблицу 3.5.
11. В конце измерительной части данной работы нужно отключить исследуемую цепь от источника питания и сам блок питания от силового щитка с помощью выключателей S1 и S1 ‘ на панели с мнемосхемой (рис. 3.26) и красной кнопки «выкл» выключателя на панели блока питания (рис. 3.27). Сообщить преподавателю об окончании измерений и приступить к вычислениям параметров цепи.
- Резонанс в электрических цепях
- Изучение электрического резонанса
- Колебательный контур
- Ток и напряжение в колебательном контуре
- Характеристики колебательного контура
- Колебательный контур с потерями энергии
- Резонанс напряжений
- Условие возникновения резонанса
- Резонансные кривые
- Добротность контура
- Резонанс в электрических цепях
- Последовательный колебательный контур. Резонанс напряжений
- Параллельный колебательный контур и резонанс токов
- Частотные характеристики сопротивлений и проводимостей реактивных двухполюсников
- Одноэлементные реактивные двухполюсники
- Двухэлементные реактивные двухполюсники
- Многоэлементный реактивный двухполюсник
- Активное сопротивление и его роль при резонансе нарпяжения.
- 📸 Видео
Видео:Резонанс напряжений в электрической цепиСкачать

Резонанс в электрических цепях
Содержание:
Резонанс в электрических цепях:
Явление резонанса можно наблюдать в любых колебательных системах, в том числе механических и электрических. Электрический резонанс возникает при определенных условиях в электрических цепях переменного тока, содержащих индуктивности и емкости.
Видео:Резонанс напряжений в электрической цепи. 11 класс.Скачать

Изучение электрического резонанса
Изучение электрического резонанса необходимо, так как это явление широко используется в технике электросвязи, а в установках сильного тока, где его возникновение специально не предусматривается, резонанс может оказаться опасным (могут возникнуть перенапряжения и пробой изоляции).
Колебательный контур
Для того чтобы понять резонансные явления, переходные процессы в электрических цепях переменного тока, которые рассматриваются далее, важно иметь представление о процессах в колебательном контуре, состоящем из идеальных катушки и конденсатора, т. е. в контуре без потерь.
Колебательный процесс в таком контуре заключается во взаимном преобразовании электрического и магнитного полей. При этом изменяется энергия полей, поэтому колебательный процесс в контуре с количественной стороны будем, как и раньше, характеризовать изменением энергии.
Ток и напряжение в колебательном контуре
Предположим, что конденсатор с емкостью С получил от источника запас энергии
В первую часть периода (0 — T/4) конденсатор разряжается и в цепи существует ток. В это время в обособленной цепи конденсатор играет роль источника энергии (рис. 17.1, б). В начальный момент ток равен нулю, далее он увеличивается. Увеличение тока в цепи вызывает возникновение э. д. с. самоиндукции eL и накопление энергии в магнитном поле катушки. Э. д. с. самоиндукции уравновешивает напряжение на конденсаторе:
Напряжение на конденсаторе в процессе разрядки уменьшается, поэтому вызываемый в цепи ток растет все медленнее, соответственно с этим уменьшается и э. д. с. самоиндукции, которая пропорциональна скорости изменения тока. Таким образом, к концу разрядки конденсатора (
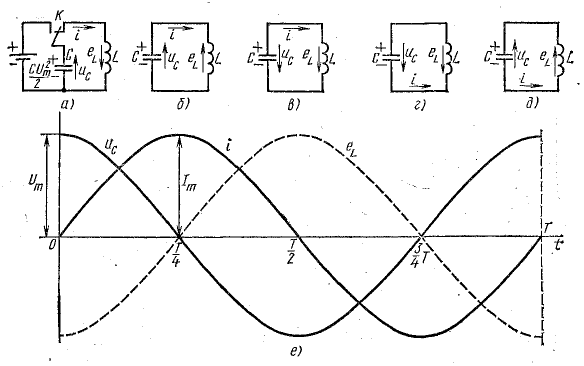
Рис. 17.1. К анализу колебательного контура
С этого момента ток начинает уменьшаться (но не прекращается), сохраняя свое направление. В следующую часть периода (от T/4 до T/2) направление тока сохраняется, потому что э. д. с. самоиндукции при уменьшении тока меняет свой знак, и роль источника энергии переходит к катушке. Уменьшающийся ток теперь является зарядным током конденсатора, заряжающегося в обратном направлении (рис. 17.1, в). Напряжение на конденсаторе увеличивается, уравновешивая теперь э. д. с. самоиндукции:
При увеличении напряжения на конденсаторе его зарядный ток уменьшается все быстрее, в результате чего э. д. с. eL увеличивается. Таким образом, к концу зарядки конденсатора напряжение на его обкладках достигает наибольшего значения, э. д. с. самоиндукции тоже максимальна, а ток становится равным нулю. Энергия магнитного поля снова перешла в энергию электрического поля . С этого момента рост э. д. с. самоиндукции прекращается и начинается ее уменьшение. Роль источника энергии снова переходит к конденсатору. Начинается третья часть периода (от Т/2 до 3T/4). В рассматриваемом процессе конденсатор второй раз становится источником энергии. Но по сравнению с первым он имеет обратную полярность, поэтому его разрядный ток изменяет направление и далее увеличивается. Снова энергия убывает в электрическом поле и накапливается в магнитном поле (рис. 17.1, г).
В момент времени t = 3T/4 напряжение на конденсаторе и э. д. с. самоиндукции становятся равными нулю, а ток — наибольшим. В последнем отрезке времени (от 3T/4 до Т) процесс протекает в том же порядке, что и во втором, но при обратном направлении тока (рис. 17.1, д).
В момент времени t = Т конденсатор заряжен в том же направлении и тем же количеством энергии, как и при t = 0. Ток переходит через нуль к положительным значениям и далее увеличивается. Процесс повторяется в порядке, рассмотренном ранее.
Характеристики колебательного контура
Энергетический процесс в колебательном контуре имеет периодический характер с периодом Т. Колебания в электрической цепи, не связанной с источником энергии, называют собственными или свободными.
Этот процесс рассмотрен по графикам изменения тока i, напряжения uC и э.д.с. eL, которые приняты синусоидальными функциями времени.
Для такого предположения имеется полное основание, так как эти величины взаимно связаны соотношением 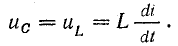
Вместе с тем ток в контуре пропорционален скорости изменения заряда конденсатора, причем он увеличивается, когда конденсатор разряжается. Следовательно, 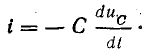
Такая взаимная связь переменных величин говорит о синусоидальном законе изменения тока и напряжения, но при наличии сдвига фаз между ними на 90°, т. е. при 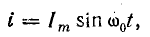
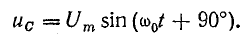
Это можно проверить: 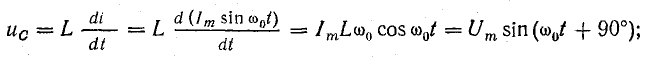
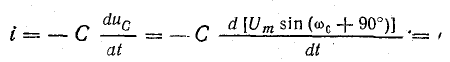
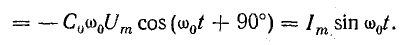
Величину ω0 в уравнениях тока и напряжения называют угловой частотой собственных колебаний в контуре. Найдем ее, используя равенство наибольшего количества энергии в конденсаторе и катушке:
и связь между амплитудами тока и напряжения:
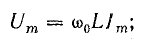
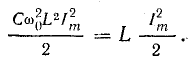
Сокращая, получим 
Частота собственных колебаний 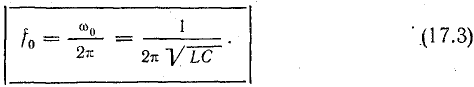
Период собственных колебаний
Из равенства (17.1) вытекает еще одно важное соотношение 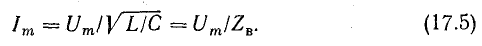
Величина, стоящая в знаменателе, имеет размерность сопротивления и называется волновым сопротивлением контура:
Колебательный контур с потерями энергии
Незатухающие колебания в контуре получаются в предположении, что потери энергии отсутствуют, т. е. R = 0.
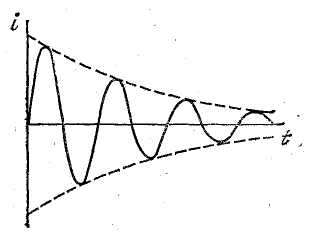
Если активное сопротивление контура не равно нулю, то запас энергии в контуре сокращается (энергия превращается в тепло), амплитуды тока и напряжения с каждым периодом убывают, как показано на рис. 17.2.
Более детальное исследование колебательного контура показывает, что частота собственных колебаний зависит от активного сопротивления: 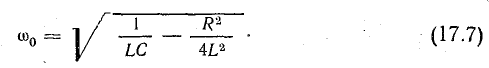
При R = 0 это выражение совпадает с (17.2).
При 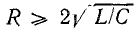
Рис. 17.2. График изменения тока в колебательном контуре с потерями
Рис. 17.3. Апериодический разряд конденсатора на катушку индуктивности
Видео:Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать

Резонанс напряжений
При рассмотрении различных режимов электрических цепей был отмечен случай равенства реактивных сопротивлений ХL = ХC при последовательном соединении элементов, содержащих индуктивность и емкость.
В этом случае электрическая цепь находится в режиме резонанса напряжений, который характеризуется тем, что реактивная мощность цепи равна нулю, ток и напряжение совпадают по фазе.
Условие возникновения резонанса
Резонанс напряжений возникает при определенной для данной цепи частоте источника энергии (частоте вынужденных колебании), которую называет резонансной частотой ωр.
При резонансной частоте, как будет показано далее, 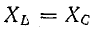
Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивного и емкостного сопротивлений, называют резонансом напряжений.
Резонанс напряжений рассмотрим, сначала на схеме идеализированной цепи (рис. 17.4, а), в которой последовательно с резистором R включены идеальные (без потерь) катушка L и конденсатор С.
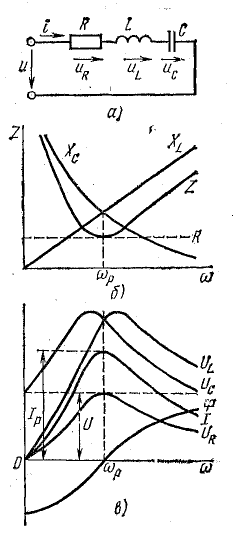
Рис. 17.4. К вопросу о резонансе напряжений
Реактивные сопротивления ХL и ХC (рис. 17.4, б) зависят от частоты вынужденных колебаний ω:
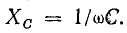
Приравнивая реактивные сопротивления и учитывая, что ω = ωр, получим 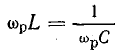
Отсюда резонансная частота 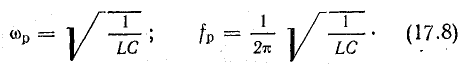
В данном случае выражение для резонансной частоты совпадает с формулой (17.3) для частоты собственных колебаний в контуре без потерь.
Основные соотношения между величинами, характеризующими режим электрической цепи и энергетические процессы. Нужно отметить, что в неразветвленной цепи обмен энергией между катушкой и конденсатором совершается через источник энергии, который восполняет потери энергии в активных сопротивлениях.
Резонансные кривые
Резонанс напряжений в цепи можно установить двумя путями: 1) изменением параметров L и С (одного из них или обоих вместе) при постоянной частоте источника или 2) изменением частоты источника энергии при постоянных L и С.
В связи с этим большой практический интерес представляют зависимости напряжений и токов на отдельных элементах цепи от частоты. Эти зависимости называют резонансными кривыми (рис. 17.4, в).
Реактивные сопротивления с изменением частоты меняются, как показано на рис. 17.4, б. При увеличении частоты ХL увеличивается пропорционально частоте, а ХC уменьшается по закону обратной пропорциональности.
Соответственно полное сопротивление Z цепи при резонансной частоте ωр оказывается наименьшим, равным активному сопротивлению R; при частоте 
Такая зависимость полного сопротивления от частоты определяет характер изменения тока при постоянном напряжении в цепи (рис. 17.4, в). При 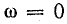
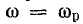
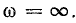
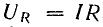
Напряжение на конденсаторе UC при 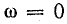
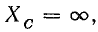
Индуктивное напряжение 

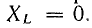
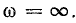
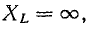
При частотах, меньших резонансной, реактивное сопротивление цепи имеет емкостный характер (отрицательно), поэтому и угол сдвига фаз в цепи отрицательный. Уменьшаясь с ростом частоты, он становится равным нулю при резонансе 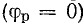
Добротность контура
При резонансе напряжений отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи (напряжению источника), равно отношению волнового сопротивления к активному. Действительно, при резонансе сопротивления реактивных элементов
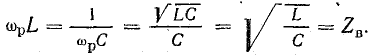
Поэтому
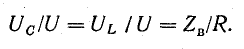
Из этого выражения следует, что при 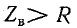
Такое превышение может оказаться значительным, если реактивные сопротивления много больше активного, и изоляция катушки или конденсатора может быть пробита. На практике подобный случай возможен, если на конце кабельной линии включается приемник, обладающий индуктивностью.
В радиотехнике качество резонансного контура считается тем выше, чем больше отношение 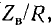
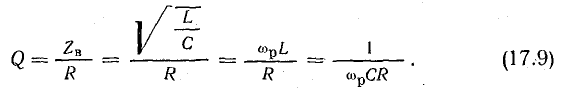
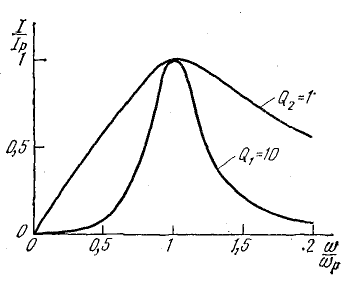
Чем меньше мощность потерь энергии в контуре (этому соответствует меньшая величина R), тем больше добротность контура.
Большей величине добротности соответствует больший ток Iр при резонансе и более острая резонансная кривая.
На рис. 17.5 показаны две резонансные кривые тока, построенные в относительных единицах при двух величинах добротности. По горизонтальной оси отложены отношения изменяющейся частоты источника энергии к резонансной частоте ω/ωр, а по вертикальной —отношения тока при данной частоте к току при резонансной частоте I/Iр.
Рис. 17.5. Резонансные кривые при двух значениях добротности контура
Все рассуждения о резонансе напряжений в идеализированной цепи можно распространить и на цепи, содержащие последовательно соединенные катушку и конденсатор с потерями. Как известно, реальные катушки и конденсатор могут быть представлены схемами последовательного соединения активного и реактивного сопротивлений (рис. 17.5). Активные сопротивления катушки и конденсатора можно рассматривать как часть общего активного сопротивления цепи R, тогда схема на рис. 17.4, а будет пригодна и в этом случае.
Видео:РЕЗОНАНС ТОКОВ в идеальной и реальной цепях │Теория ч. 1Скачать
Резонанс в электрических цепях
Резонансные (колебательные) цепи:
Резонансными или колебательными цепями называются электрические цепи, в которых могут возникать явления резонанса напряжений или токов.
Резонанс представляет собой такой режим пассивной электрической цепи, содержащей индуктивности и емкости, при котором реактивное сопротивление и реактивная проводимость цепи равны нулю; соответственно равна нулю реактивная мощность на выводах цепи.
Резонанс напряжения наблюдается в электрической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных элементов r, L и С, рассмотренная, представляет собой один из простейших случаев такой цепи. В радиотехнике ее называют последовательным колебательным контуром.
При резонансе напряжений индуктивное сопротивление одной части цепи компенсируется емкостным сопротивлением другой ее части, последовательно соединенной с первой. В результате реактивное сопротивление и реактивная мощность на выводах цепи равны нулю.
В свою очередь резонанс токов наблюдается в электрической цепи с параллельным соединением участков, содержащих индуктивности и емкости. Один из простейших примеров такой цепи, состоящей из параллельно соединенных элементов r, L и С. В радиотехнике такую цепь называют параллельным колебательным контуром.
При резонансе токов индуктивная проводимость одной части цепи компенсируется емкостной проводимостью другой ее части, параллельно соединенной с первой. В результате реактивная проводимость и реактивная мощность на выводах цепи равны нулю.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Исследование резонансных режимов в электрических цепях заключается в нахождении резонансных частот,
зависимостей различных величин от частоты 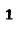
Резонансные цепи очень широко применяются в электротехнике и представляют собой неотъемлемую часть всякого радиотехнического устройства. Изучению явления резонанса, свойств и частотных характеристик простейших резонансных цепей посвящена данная глава.
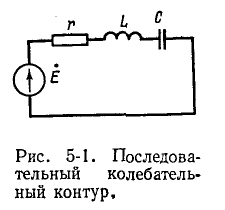
Последовательный колебательный контур. Резонанс напряжений
Резонансная цепь с последовательным соединением r, L и С (рис. 5-1) является простейшей цепью для изучения явления резонанса напряжений и подробно рассматривается ниже. Комплексное сопротивление такой цепи зависит от частоты:
Резонанс напряжений наступает при частоте 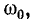
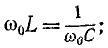
отсюда
Мгновенные энергии выражаются формулами:
Если принять
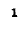
Максимальные значения этих энергий равны друг другу, так как
Это следует и из того, что реактивное сопротивление цепи, содержащей индуктивность и емкость, при любой схеме соединений пропорционально разности максимальных значений энергии, запасаемой в магнитном и электрическом полях:
Поэтому условию резонанса (х = 0) соответствует равенство
Мгновенные значения 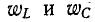
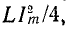
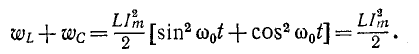
В рассматриваемом случае (резонанс напряжений, рис. 5-1) в цепи не происходит обмена энергии между источником и реактивными элементами цепи, а вся электрическая энергия, поступающая от источника, расходуется в сопротивлении r.
Мы уже встречались с понятием добротности индуктивной катушки 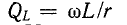
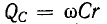
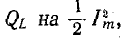
Здесь 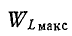
Аналогично рассуждая, т. е. умножив и разделив выражение 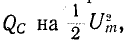
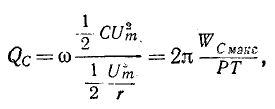
где 
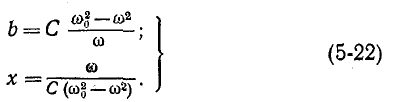
В случае резонансной цепи также пользуются понятием добротности цепи, подразумевая под этим в общем случае величину

здесь 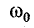
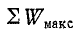
Знак 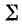
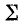
Для схемы рис. 5-1 на основании (5-3) получаем:
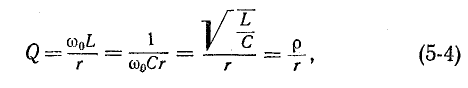
где 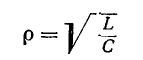
называется характеристическим (а также волновым) сопротивлением резонансного контура.
Условимся называть относительной расстройкой частоты по отношению к резонансной
частоте контура величину
Сопротивление контура согласно (5-1) и с учетом (5-2) и (5-4)
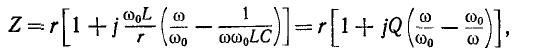
откуда, используя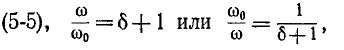
Следовательно, полное сопротивление цепи 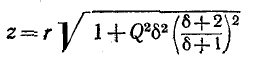
и угол
Ток в цепи 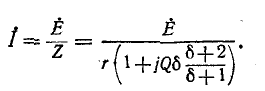
При частоте, близкой к резонансной, 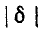
Выражения (5-7) практически достаточно точны при 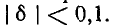
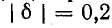
На рис. 5-2 кривые даны в относительных значениях: по оси абсцисс отложена относительная расстройка частоты 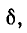
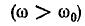
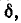
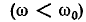
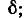
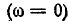
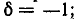
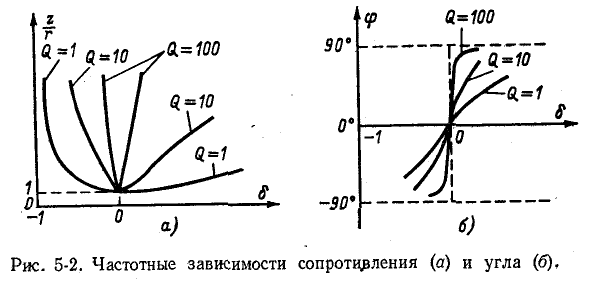
Полное сопротивление цепи минимально при резонансе напряжений при этом ток в цепи достигает своего максимального значения
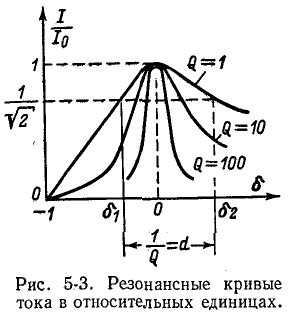
На рис. 5-3 изображены резонансные кривые тока в относительных значениях: по оси абсцисс, как и на предыдущих графиках, отложены значения 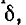
Чем выше добротность цепи Q, тем острее резонансные кривые. Таким образом, величина Q характеризует остроту резонансной кривой («остроту настройки»); согласно (5-3) чем больше отношение максимума энергии поля реактивного элемента к количеству теплоты, рассеиваемой за один период в резонансном контуре, тем острее резонансная кривая.
Резонансные кривые были построены здесь в зависимости от относительной расстройки частоты 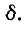
вывести расчетные выражения и построить резонансные кривые в зависимости от 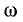
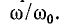
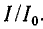
Полосу частот вблизи резонанса, на границах которой ток снижается до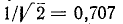
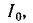
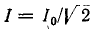
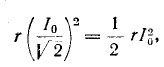
т. е. составляет половину мощности, расходуемой при резонансе. Поэтому полосу пропускания характеризуют как полосу, границы которой соответствуют половине максимальной мощности. На границах полосы пропускания резонансного контура активное и реактивное сопротивления равны 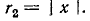
что дает
Соответственно и фазовый сдвиг между напряжением на выводах цепи и током составляет 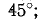
На основании (5-8) условие для границы полосы пропускания записывается в следующем виде:
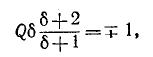
откуда
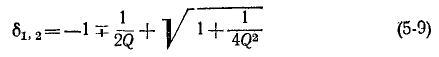
(знак минус перед корнем, получающийся в результате решения квадратного уравнения, опускается, как не имеющий смысла). Индексы 1 и 2 и соответственно знаки минус и плюс в выражении (5-9) относятся к границам ниже и выше резонанса.
По определению полоса пропускания резонансного контура находится из условия

Величина d, обратная добротности контура, называется затуханием контура.
При достаточно высокой добротности резонансного контура 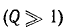
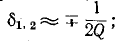
В радиотехнических устройствах к одному из реактивных элементов колебательного контура, например емкости, подключается нагрузка в виде сопротивления 
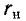
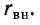
Так как обычно 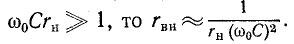
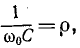
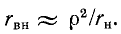
Таким образом, добротность нагруженного контура равна:
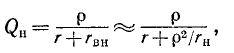
а затухание увеличивается на вносимое затухание
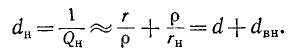
Если вносимое сопротивление 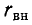
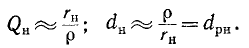
Внутреннее сопротивление источника э. д. с. 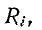
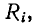
контура. Поэтому с точки зрения сокращения полосы пропускания последовательного колебательного контура выгоден источник напряжения с малым внутренним сопротивлением.
В условиях, близких к резонансу, напряжения на индуктивности и емкости могут быть весьма велики, что необходимо учитывать во избежание повреждения изоляции.
На рис. 5-4 показана векторная диаграмма тока и напряжений при резонансе. Напряжения на реактивных элементах при резонансе определяются из выражения
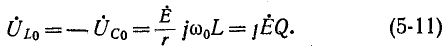
При Q > 1 эти напряжения превышают напряжение U — Е, приложенное к резонансному контуру. Однако значения, получаемые на основании (5-11), не являются максимальными: максимум напряжения 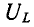
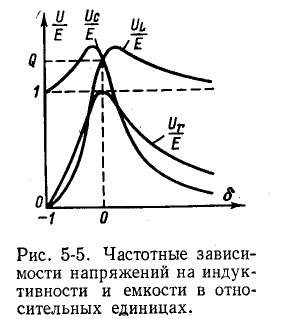
несколько выше (правее), а максимум Uc — ниже (левее) резонансной частоты (рис. 5-5).
Напряжение на индуктивности 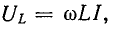
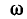
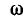
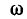
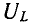
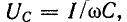
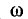
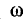
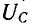
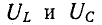
Эго также вытекает из анализа следующих ниже выражений, полученных с учетом (5-5) и (5-6):
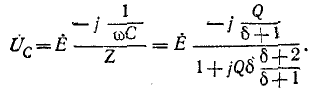
Напряжение 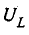
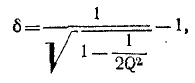
а напряжение
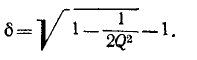
Пренебрегая 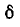
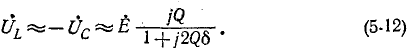
Возвращаясь к определению понятия добротности рассматриваемой резонансной цепи, мы видим, что наряду с формулами (5-3) и (5-4) добротность цепи характеризуется выражениями (5-10) и (5-11), а именно: 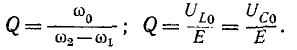
Последняя формула показывает, что добротность рассматриваемой цепи определяется как кратность перенапряжения на L и С при резонансной частоте.
Выше была рассмотрена неразветвленная электрическая цепь с последовательно соединенными r, L н С. Для исследования явления резонанса в более сложных разветвленных цепях, где резонанс напряжений может возникать на одной или нескольких частотах, наряду с аналитическим методом расчета, иллюстрированным выше, целесообразно также пользоваться методом геометрических мест.
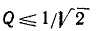
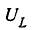
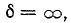
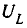
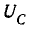
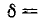

Параллельный колебательный контур и резонанс токов
Явление резонанса токов удобно изучать применительно к электрической цепи с параллельно соединенными r, L и С (рис. 5-6), так как при этом можно непосредственно воспользоваться результатами, полученными в предыдущем параграфе.
Действительно, выражение для комплексной проводимости такой цепи
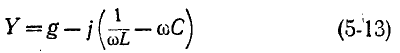
по своей структуре аналогично выражению (5-1), причем резонансная частота определяется согласно (5-2).
Добротность резонансной цепи на основании (5-3)
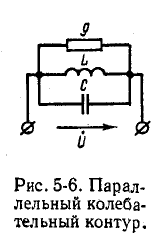
По аналогии с предыдущим выражение (5-13) приводится к виду:
Сравнивая полученный результат с (5-6), убеждаемся в том, что выражение Y/g для схемы рис. 5-6 имеет тот же вид, что и выражение 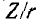
Поэтому кривые рис. 5-2 применимы и в данном случае: кривые рис. 5-2, а выражают зависимость от 6 Отношения y/g, а кривые рис. 5-2, б — зависимость угла —
Кривые рис. 5-2, а показывают, что при резонансе токов полная проводимость цепи минимальна, т. е. входное сопротивление достигает максимума.
При заданном напряжении 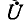
Этот ток достигает минимума при резонансной частоте, так как при этом
Следовательно, отношение. токов 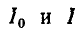
правая часть которого полностью совпадает с (5-8).
В связи с этим резонансные кривые рис. 5-3 выражают применительно к схеме рис. 5-6 зависимость
В случае резонанса токов токи в индуктивном и емкостном элементах схемы рис. 5-6 равны и противоположны по знаку:
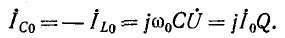
Полученное выражение показывает, что добротность рассматриваемой цепи определяется как кратность токов в L и С по отношению к суммарному току
При Q > 1 эти токи превышают
Если параллельный колебательный контур питается от источника тока с внутренним сопротивлением 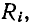
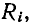
Для схемы рис. 5-6 при резонансе токов остается в силе вывод, сделанный в предыдущем параграфе о непрерывном обмене энергией между индуктивным и емкостным элементами при резонансе напряжений.
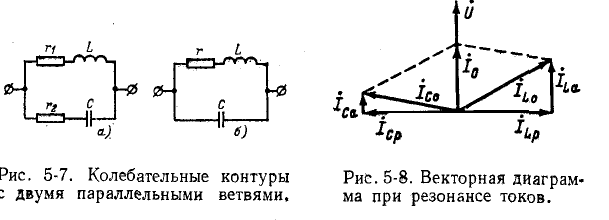
Схема рис. 5-6 является идеализированной, так как она не учитывает активных потерь в ветвях L и С. Поэтому рассмотрим другие схемы,’приняв во внимание активные сопротивления в ветвях L и С (рис. 5-7, а и б).
Условие резонанса токов для схемы рис. 5-7, а записывается в виде равенства реактивных проводимостей:
Явление резонанса возможно при этом только в случае, если подкоренное выражение (5-15) имеет положительный
знак или, что то же, величины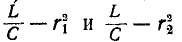
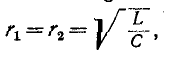
.
На рис. 5-8 показана векторная диаграмма при резонансе токов в цепи рис. 5-7, а. Токи в индуктивной и емкостной ветвях слагаются из активных 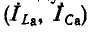
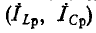
Чем меньше 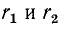
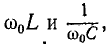
к 
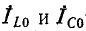
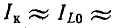
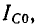
При резонансе вся цепь имеет только активную проводимость
откуда с учетом (5-14) 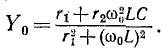
Для колебательного контура с малыми потерями можно пренебречь слагаемым 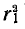
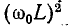
что 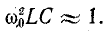
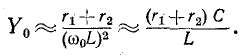
При 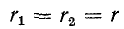
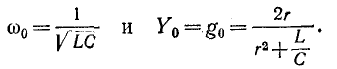
Кроме того, если 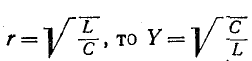
частоте (резонанс в такой цепи называют «безразличным» резонансом).
Легко убедиться в том, что и в. случае резонансной цепи с двумя параллельными ветвями (см. рис. 5-7) соблюдается условие 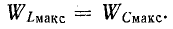
умножить обе части уравнения (5-14) на
Выше отмечалось, что в схеме с параллельно соединенными r, L и С (см. рис. 5-6) полная проводимость всей цепи имеет минимум при резонансной частоте.
Для схемы рис. 5-7, б нетрудно показать, что при изменении частоты о) или индуктивности L минимум полной проводимости цепи, а также минимум общего тока наступают не при резонансной частоте. В том же случае, когда переменным параметром является емкость С, проводимость и общий ток достигают минимума при резонансе токов.
Добротность параллельного колебательного контура рис. на основании (5-3) равна:
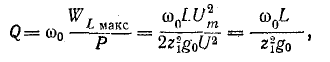
но 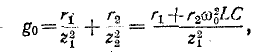
откуда 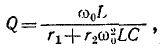
где резонансная частота 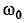
Часто в ветви с емкостью сопротивлением 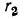
Рассмотрим этот случай (см. рис. 5-7, б).
Резонанасная частота такого контура согласно (5-15) 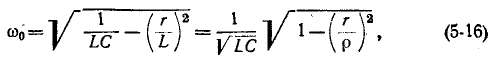
а добротность цепи в соответствии с полученным выше выражением 
Из сопоставления (5-16) и (5-2) видно, что при одних и тех же параметрах r, L и С резонансные частоты для схем рис. 5-1 и 5-7, б отличаются множителем
При 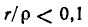
Общее сопротивление колебательного контура (см. рис, 5-7, б) 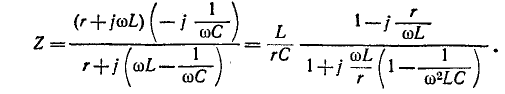
На основании соотношений (5-16) и (5-17) можно получить: 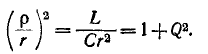
Учитывая также соотношения 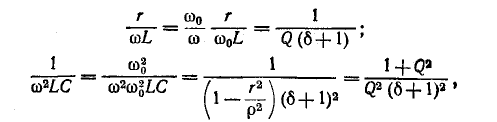
получаем выражение для сопротивления колебательного контура:
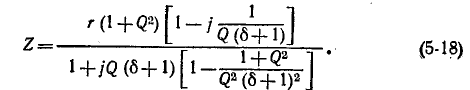
При резонансной частоте
В тех случаях, когда 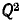
В режиме, близком к резонансу, когда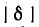
При высокой добротности колебательного контура
Приэтом токи в ветвях 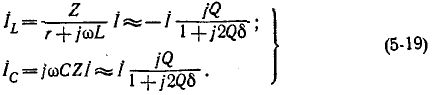
Здесь 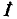
Напряжение на выводах цепи 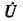
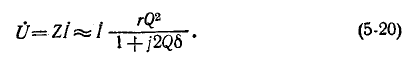
Приближенные выражения (5-19) и (5-20) аналогичны при заданном Q выражениям(5-12) и (5-7), выведенным для цепи рис. 5-1, при условии замены напряжений токами и обратно. Поэтому кривые сопротивлений, токов и напряжений, соответствующие схеме рис. 5-1, в известном масштабе приближенно выражают проводимости, напряжения и токи в схеме рис. 5-7, б.
Следует обратить внимание на то, что в схеме рис. 5-6 мгновенная мощность в цепи при резонансе токов равна мгновенной мощности, расходуемой в сопротивлении r; в схемах с двумя параллельными ветвями (рис. 5-7) мгновенная мощность на выводах цепи отлична от мгновенной мощности, расходуемой в сопротивлениях ветвей. Например, в тот момент, когда ток, входящий в цепь, проходит через нулевое значение, мгновенная мощность на выводах цепи равна нулю; в этот момент токи в ветвях, сдвинутые по фазе относительно суммарного тока цепи, отличны от нуля и поэтому мгновенная мощность, расходуемая в сопротивлениях ветвей, также не равна нулю. Объясняется это тем, что в схемах
рис. 5-7, а и б энергия, накапливаемая реактивными элементами, периодически преобразуется частично в теплоту (в сопротивлениях ветвей), а затем вновь пополняется за счет энергии источника.
Для повышения крутизны резонансных характеристик, необходимой для более четкого разделения колебаний разных частот, в радиотехнике широко применяются двухконтурные резонансные цепи: два резонансных контура, настроенных каждый в отдельности на одну и ту же частоту, связываются индуктивно или электрически. В отличие от «одногорбой» резонансной кривой одиночного контура в связанных цепях получаются «двугорбые» кривые; например, ток в каждом контуре может иметь максимумы при двух частотах, расположенных ниже и выше резонансной частоты одиночного контура.
Частотные характеристики сопротивлений и проводимостей реактивных двухполюсников
Двухполюсником называется любая электрическая цепь или часть электрической цепи, имеющая два вывода. Ниже рассматриваются только линейные двухполюсники, т. е. такие, которые состоят из линейных элементов.
Различают двухполюсники активные и пассивные.
Активным называется двухполюсник, содержащий источники электрической энергии, которые не компенсируются взаимно внутри двухполюсника.
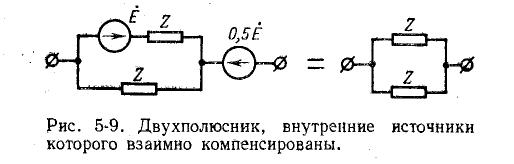
Пассивным называется двухполюсник, не содержащий источников электрической энергии; в случае линейного двухполюсника он может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжение на его разомкнутых выводах равно нулю. Такой линейный двухполюсник относится к категории пассивных; его сопротивление, измеренное на выводах, не изменится, если источники электрической энергии внутри него заменить пассивными элементами — внутренними сопротивлениями источников э. д. с. или соответственно внутренними проводимостями источников тока. Пример двухполюсника, содержащего компенсированные источники, показан на рис. 5-9.
По числу элементов, входящих в двухполюсник, различают одноэлементный, двухэлементный и многоэлементный двухполюсники.
По характеру этих элементов двухполюсники делятся на реактивные, т. е. состоящие из индуктивностей и емкостей, и двухполюсники с потерями, содержащие активные сопротивления. Реактивные двухполюсники представляют собой идеализированные электрические системы, приближающиеся по своим свойствам к физически существующим цепям с малыми потерями.
Частотные характеристики сопротивлений или проводимостей двухполюсников, образующих электрическую цепь, предопределяют частотные и резонансные свойства цепи, т. е. зависимости амплитуд и фаз токов и напряжений от частоты.
Настоящий параграф посвящен изучению частотных характеристик пассивных реактивных двухполюсников.
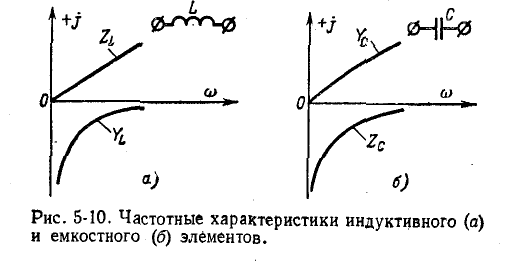
Одноэлементные реактивные двухполюсники
Индуктивность и емкость представляют собой простейшие одноэлементные реактивные двухполюсники. Знак комплексного сопротивления и комплексной проводимости каждого из этих двухполюсников не зависит от частоты; этим они существенно отличаются от других, более сложных реактивных двухполюсников, содержащих неоднородные реактивные элементы, т. е. индуктивность и емкость в разных сочетаниях.
Комплексное сопротивление индуктивного элемента во всем спектре частот имеет положительный знак, а комплексная проводимость — отрицательный:
Комплексное сопротивление емкостного элемента во всем спектре частот имеет отрицательный знак, а комплексная проводимость — положительный:
В рассматриваемом случае реактивных двухполюсников комплексные сопротивления и проводимости являются мнимыми. Поэтому для сохранения знаков частотные ха-рактернстнкн сопротивлений и проводимостей удобно рисовать в прямоугольной системе координат, в которой вверх откладываются мнимые величины со знаком плюс, а вниз — со знаком минус.
Частотные характеристики 
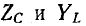
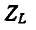
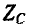
Следует заметить, что как сопротивления, так и проводимости рассматриваемых здесь одноэлементных реактивных двухполюсников возрастают (с учетом знака) по мере повышения частоты, т. е.
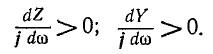
Это является общим свойством всех реактивных двухполюсников, а не только одноэлементных.
Двухполюсник, состоящий из последовательно или параллельно соединенных однородных элементов (индуктивностей или емкостей), относится к числу одноэлементных двухполюсников, так как последовательно или параллельно соединенные однородные элементы могут быть заменены одним эквивалентным реактивным элементом того же характера.
Двухэлементные реактивные двухполюсники
Двухэлементные двухполюсники, составленные из индуктивности и емкости, представляют собой простейшие резонансные цепи.
При последовательном соединении индуктивности и емкости алгебраически складываются комплексные сопротивления. На рис. 5-11, а жирной линией показана частотная характеристика двухполюсника, полученная в результате графического сложения кривых 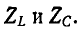
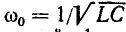
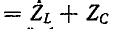

Частотная характеристика проводимости того же двухполюсника представляет собой функцию, обратную сопротивлению:
Кривая Y показана на рис. 5-11, б.
При резонансной частоте проводимость рассматриваемого двухполюсника обращается в бесконечность; эта точка носит название полюса функции Y и обозначается на чертеже крестиком
Частотные характеристики Z и Y, построенные таким образом1, соответствуют уравнениям:
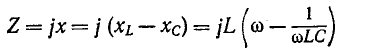
и 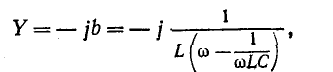
или с учетом(5-2):
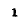
В области частот ниже резонансной 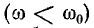
В области частот выше резонансной 
При параллельном соединении индуктивности и емкости алгебраически складываются их комплексные проводимости. На рис. 5-12, а жирной линией показана частотная 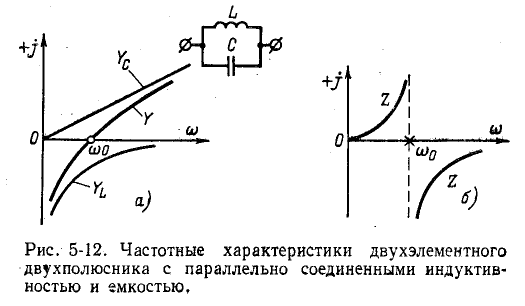
характеристика двухполюсника, полученная в результате графического сложения
Частотная характеристика сопротивления того же двухполюсника представляет собой функцию, обратную проводимости: Z — 1/Y. Кривая Z показана на рис. 5-12, б.
Частота, при которой характеристика Y пересекает ось абсцисс (нуль функции У), а характеристика Z уходит в бесконечность (полюс функции Z), является резонансной частотой (резонанс токов).
Частотные характеристики, построенные на рис. 5-12, соответствуют уравнениям: 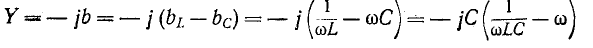
И
или с учетом (5-22)
В области частот ниже резонансной проводимость индуктивного элемента перекомпенсирует проводимость емкостного элемента и сопротивление двухполюсника получается, индуктивным. В области частот выше резонансной наблюдается обратное явление и сопротивление двухполюсника имеет емкостный характер.
Таким образом, в зависимости от частоты двухэлементный реактивный двухполюсник может иметь либо индуктивное, либо емкостное сопротивление. При этом, так же как и в случае одноэлементного реактивного двухполюсника, кривые Z и Y возрастают, т. е. производные от 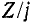
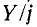
В отличие от сопротивлений одноэлементных двухполюсников, которые выражаются только через текущую частоту, сопротивления двухэлементных реактивных двухполюсников зависят также и от разности квадратов резонансной и текущей частот (формулы (5-21) и (5-22)1.
Как видно из выражений (5-21), для построения частотных характеристик двухполюсника, состоящего из последовательно соединенных элементов L и С, достаточно знать нуль функции Z или, что то же, полюс функции Y. Параметр L, входящий в (5-21), влияет только на выбор масштаба Z и Y по оси ординат.
Аналогично в соответствии с (5-22) для построения частотных характеристик двухполюсника, состоящего из параллельно соединенных элементов L и С, достаточно знать полюс Z или, что то же, нуль Y, причем параметр С влияет только на масштаб Z и Y.
Двухполюсники, имеющие одинаковые частотные характеристики Z или Y, эквивалентны.
Многоэлементный реактивный двухполюсник
Многоэлементный реактивный двухполюсник может быть получен в результате различных сочетаний одноэлементных и двухэлементных двухполюсников. Пользуясь частотными характеристиками, приведенными выше, можно построить частотные характеристики для трех-, четырех- и много-элементных реактивных двухполюсников. При этом одно-
родные элементы (или группы элементов с одинаковыми резонансными частотами), соединенные параллельно или последовательно, должны быть сначала заменены одним элементом (или эквивалентной группой элементов, как это, например, показано на рис. 5-13).
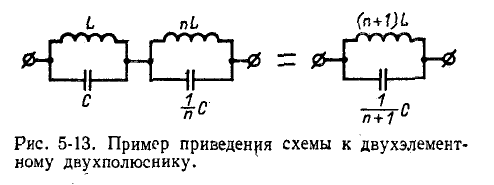
Такие двухполюсники будем называть «приведенными».
Из свойства положительности производной 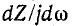
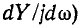
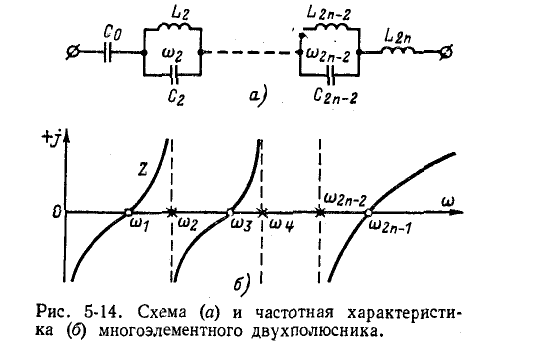
В общем случае, если при 
В противном случае порядок расположения резонансов обратный: первым наступает резонанс напряжений, вторым — резонанс токов и т. д.
На рис. 5-14, а дана схема многоэлементного двухполюсника, а на рис. 5-14, б — соответствующая ему частотная характеристика сопротивления.
У реактивных двухполюсников сумма чисел полюсов и нулей (не считая точек 
Расположение нулей и полюсов, как указывалось выше, поочередное, а все ветви частотной характеристики с увеличением 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Соединение звездой и треугольником в трехфазных цепях
- Принцип действия асинхронного и синхронного двигателей
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока
- Расчет неразветвленной однородной магнитной цепи
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Активное сопротивление и его роль при резонансе нарпяжения.
В чем заключается резонанс напряжений и условия его возникновения.
Явление резонанса электрических напряжений наблюдается в последовательной R-L-C цепи при условии равенства реактивных сопротивлений L и C. Для обеспечения энергетической подпитки колебательного контура в последовательную цепь включается также источник электродвижущей силы Е. Источник вырабатывает переменное напряжение с частотой W. При резонансе ток, циркулирующий в последовательной цепи, должен совпадать по фазе с ЭДС (Е). Это обеспечивается, если общее сопротивление схемы
Z = R+j(Xl-Xc) будет лишь активным, т.е. Z=R.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а, следовательно, и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а, следовательно, и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Опасность резонанса напряжений.
Состоит в том, что в схеме могут находиться элементы, которые не рассчитаны на высокое напряжение или на высокий ток нагрузки, как следствие, они могут выйти из строя. Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробоя изоляции.
В тоже время, резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике в различных приборах и устройствах, основанных на резонансных явлениях. Радиоприемники настраиваются на волну( частоту) радиостанции путем изменения емкости. При резонансе, частота передающей станции и частота контура L-C совпадают, что приводит к значительному усилению только этого сигнала на входе приемника.
Активное сопротивление и его роль при резонансе нарпяжения.
В электрической цепи переменного тока существует два вида сопротивлений: активное и реактивное. Это является существенным отличием от цепей постоянного тока.
Активное сопротивление
При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.
Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле
Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.

Активное сопротивление r при резонансе напряжений играет роль трения, причем при его увеличении добротность снижается. Сопротивление такой цепи в комплексной форме запишется в виде:
📸 Видео
РЕЗОНАНС ТОКОВ В РЕАЛЬНОЙ ЦЕПИ │Теория ч. 2Скачать

Задача на резонанс│Как найти резонансную частоту при смешанном соединении RLC│Электротехника ТОЭСкачать

Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Обратная мощность резонанса, схема ТеслыСкачать

Реактивная мощность за 5 минут простыми словами. Четкий #энерголикбезСкачать

Урок 363. Мощность в цепи переменного токаСкачать

Резонанс в R-L-C-цепиСкачать

Резонанс в электрической цепиСкачать

Задача на Резонанс НАПРЯЖЕНИЙ с Тремя реактивными элементамиСкачать

КАК РАБОТАЕТ LC ЦЕПЬ | РЕЗОНАНССкачать

Что такое РЕЗОНАНС ТОКОВ | Самое понятное объяснениеСкачать

Задача на Резонанс Токов с Тремя реактивными элементамиСкачать

Баланс мощностей | Активная мощностьСкачать

Резонансы токов и напряженийСкачать