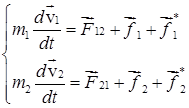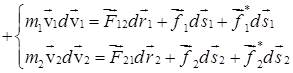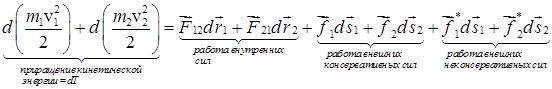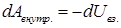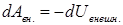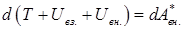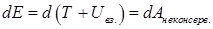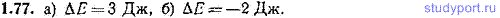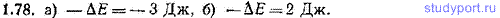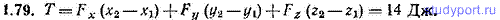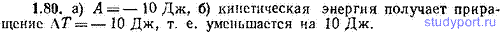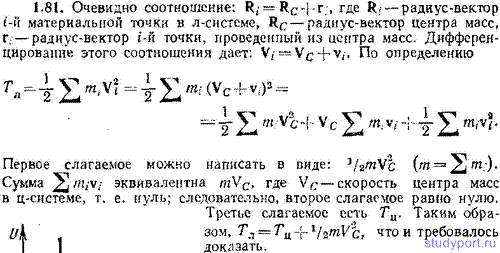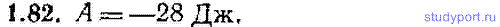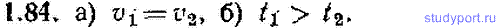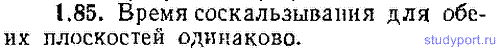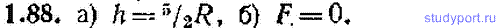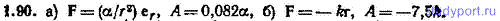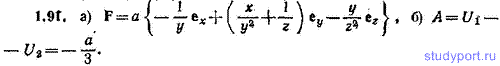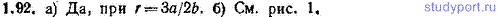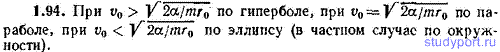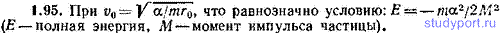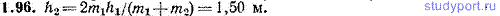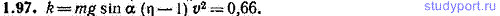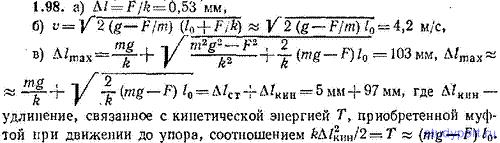Уравнение морзе описывающее потенциальную энергию системы состоящей из двух частиц имеет вид

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Лекция №1. Квантов0механическ0е обоснование теории строения молекул и химической связи. Строение атома (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Из различных методов определения СЭ наиболее прямой и точный — измерение минимальной энергии фотоотрыва электрона от отрицательного иона.

Для большинства атомов присоединение электрона — экзотермический процесс. Наиболее высоким по абсолютной величине сродством к электрону обладают атомы галогенов в последовательности Cl > F > Вг > I. Энергии ионизации и сродство к электрону молекул определяют также, как это сделано для атома.

ТЕОРЕТИЧЕСКИЕ МЕТОДЫ, ПРИМЕНЯЕМЫЕ ПРИ ИЗУЧЕНИИ СТРОЕНИЯ МОЛЕКУЛ И ХИМИЧЕСКОЙ СВЯЗИ

Видео:Потенциальная и Кинетическая🤔Скачать

1. Молекула. Потенциальная поверхность. Равновесная конфигурация

2. Теория химической связи и её задачи.

3. Вариационный метод решения уравнения Шрёдингера.

§1. Молекула. Потенциальная поверхность. Равновесная конфгурация.

В химии молекулой называют наименьшую частицу данного вещества, обладающую его химическими свойствами, способную к самостоятельному существованию. Если отвлечься от поступательного движения молекулы как целого, то в ее энергию вносят вклад три вида движения: 1) движение электронов в поле ядер, 2) колебание ядер около положения равновесия и вращение молекулы вокруг оси, проходящей через центр масс, причем Еэл >> Екол >>Евр.

Хотя эти движения взаимосвязаны, можно приближенно рассматривать их как независимые и считать энергию молекулы равной сумме электронной, колебательной и вращательной энергий:

Е = Еэл + Екол +Евр. (6.1)

Волновая функция молекулы в этом приближении равна произведению функций, описывающих указанные три вида движения:

(6.2)

Остановимся на наиболее важной составляющей энергии молекулы — электронной энергии. Так как скорость тяжелых ядер во много раз меньше скорости легких электронов, приближенно можно рассматривать движение электронов в молекуле в каждый данный момент, считая ядра неподвижными (приближение Борна — Оппенгеймера). Выбранному фиксированному положению ядер R отвечает определенная энергия электронов , включающая их кинетическую энергию, энергию взаимодействия электронов друг с другом и энергию взаимодействия электронов с ядрами.

Условимся включать сюда также энергию отталкивания ядер . Тогда название «электронная» для указывает, что учитывается движение только электронов, но не ядер, а фиксированное расстояние между ядрами R рассматривается как параметр. Индекс «эл» при этом можно опустить (Eкол и Евр здесь не рассматриваются). Если расстояние между ядрами R изменится, изменится поле ядер, в котором движутся электроны, изменится и электронная энергия системы . В этом смысле электронная энергия есть функция межъядерного расстояния и по отношению к движению ядер играет роль потенциальной энергии. Вид функции для двухатомной молекулы АВ изображает кривая о рис. 5.1., называемая потенциальной кривой. Когда атомы А и В удалены на бесконечное расстояние, электронная энергия равна сумме электронных энергий невзаимодействующих атомов А и В в основном состоянии: .

При сближении ядер электронная энергия понижается (сила притяжения электронов к ядрам преобладает над силами отталкивания между ядрами и между электронами). Затем потенциальная кривая проходит через минимум при R = rе и при дальнейшем сближении ядер возрастает, стремясь к бесконечности при R →0 (преобладает сила отталкивания). Межъядерное расстояние R=re, отвечающее минимуму потенциальной кривой, называется равновесным. При R=re равнодействующая всех сил притяжения и отталкивания равна нулю, молекула находится в устойчивом состоянии. Этому состоянию отвечает строго определенное значение электронной энергии молекулы. За нуль отсчета энергии можно принять, как и для атома, энергию невзаимодействующих электронов и ядер. Разность между суммой энергий невзаимодействующих атомов и Eэл. мол называют энергией химической связи или энергией диссоциации молекулы, отсчитанной от минимума потенциальной кривой, и обозначают De (глубина «потенциальной ямы»):

Данная потенциальная кривая соответствует классическим представлениям. Однако в нее надо внести поправки, так как равновесное состояние неосуществимо с точки зрения квантовой механики: в этом состоянии ядра неподвижны, значит, одновременно точно определены координата (R = rе) и импульс (р = 0), что противоречит соотношению неопределенностей Гейзенберга. Параметры rе и De (рис. 6.1) относятся таким образом к гипотетическому равновесному состоянию. В действительности даже и при 0К ядра не зафиксированы при R — rе, а совершают колебания около положения равновесия. Реальная энергия молекулы при этом выше, чем предполагалась, на величину энергии «нулевых колебаний» (рис.6.1). При нулевых колебаниях расстояние R между ядрами изменяется, в результате чего нулевой колебательный уровень характеризуется некоторым усредненным значением r0, которое из-за асимметрии потенциальной кривой незначительно, отличается от гипотетического равновесного расстояния rе=0,751·10-10 м и 0,741·10-10 м соответственно для Н2).

Определяемая на опыте энергия диссоциации молекулы D0 отсчитывается не от минимума потенциальной кривой как De, а от уровня нулевых колебаний (рис.и связана с De соотношением

(6.4)

Энергия диссоциации D0, служит мерой прочности химической связи и определяется как изменение энергии в процессе — АВ = А + В при 0 К в идеально-газовом состоянии. Если специальных указаний нет, то понимается, что как молекула АВ, так и атомы А и В находятся в основном электронном состоянии. Это определение сохраняет силу и для многоатомных молекул. Например, для молекулы AmBn энергией диссоциации будет изменение энергии в процессе AmBn = mA + nB.

Потенциальная поверхность. Равновесная конфигурация. При описании потенциальной кривой вместо Eэл. мол обычно используют символ E(R) или Е. Для многоатомной молекулы Е является функцией уже не одной, а нескольких пространственных координат Rij. Например, потенциальная энергия молекулы ABC является функцией трех независимых координат — R1(A — В), R2(B — С) и угла о(АВС) или расстояний R1(A — В), R2(B — С) и R3(А — С).

Для линейной молекулы с фиксированным углом α- 180° эта функция изобразится поверхностью в трехмерном пространстве (потенциальная поверхность) Устойчивому состоянию молекулы отвечает минимальное значение ее энергии E(АВС) и определенное относительное расположение ядер в пространстве, называемое равновесной конфигурацией молекулы с параметрами rе(А — В) и rе(В — С). Глубина потенциальной ямы определяет энергию химической связи De и по формуле (5.4) энергию диссоциации молекулы D0.

Для более сложной молекулы, чем линейная ABC, равновесная конфигурация и энергия равновесного состояния определяются положением минимума на потенциальной поверхности в многомерном пространстве. Если потенциальная поверхность имеет два (или более) минимума, для молекулы возможны два изомера или более, отличающиеся параметрами равновесной конфигурации и энергией. Если минимума на потенциальной поверхности нет, данная система нестабильна, при любом расположении ядер она распадается на невзаимодействующие атомы.

Так же как и атом, молекулу можно перевести в возбужденные электронные состояния (энергия возбуждения Те), каждому из которых отвечает своя потенциальная поверхность или кривая (кривая б на рис. 6.1).

Рассмотрев потенциальную кривую (поверхность), можно дать еще одно определение молекулы молекула — физически устойчивая система, состоящая из двух (или более) ядер и определенного числа электронов, состояние которой описывается потенциальной кривой (поверхностью) с минимумом.

Говоря о физической устойчивости, понимают, что соединение атомов в молекулу сопровождается понижением энергии системы. Данным здесь определением охватываются кроме обычных молекул (Н2, СН4 и др.) также радикалы (СН, ОН, СН3 и др.) и молекулярные ионы (Н+, O2— и др.). Этому отвечает одинаковый подход теории строения к изучению перечисленных типов частиц. В тех случаях, когда молекулы одноатомны (благородные газы, пары металлов), сохраняет силу аналогичное определение для атома.

Равновесная конфигурация предполагает жесткую фиксацию всех межъядерных расстояний в молекуле. Однако реальная молекула не является жесткой системой. Вместе с тем у огромного большинства молекул амплитуды колебаний ядер весьма малы по сравнению с межъядерными расстояниями и можно, пренебрегая колебаниями, рассматривать молекулы как жесткие системы («квазижесткие» или «квазитвердые» молекулы).

Равновесные конфигурации молекул принято относить к тем или иным точечным группам симметрии.

Двухатомные молекулы подразделяются на молекулы с одинаковыми ядрами, или гомонуклеарные (например, Н2), и с неодинаковыми ядрами, или гетеронуклеарные (например, HCI). Свойства симметрии их различны.

Симметрия равновесной конфигурации определяет и симметрию электронного облака молекулы. В связи с этим гомонуклеарные и гетеронуклеарные молекулы различаются по электрическим и оптическим свойствам, таким, как дипольный момент, поляризуемость и магнитная восприимчивость, правила отбора в спектрах. То же относится и к многоатомным молекулам, различающимся по симметрии, как, например, СН4 и СН3С1.

Рассмотренные молекулярные параметры: энергия диссоциации, межъядерные расстояния, равновесная конфигурация важны для химии не только как индивидуальные характеристики молекул. По ним можно рассчитать термодинамические свойства веществ и константы равновесия химических реакций.

§2. Теория химической связи и ее задачи. Уравнение Шредингера для молекул

Взаимодействие атомов, приводящее к образованию молекул простых и сложных веществ, а также кристаллов, называют химической связью. Взаимодействие атомов многообразно, поэтому многообразны и химические связи, которые часто сводят к нескольким основным типам: ковалентной, ионной, донорно-акцепторной, водородной связи и др. Однако все эти взаимодействия можно описать с позиций единой теории химической связи.

1) Эта теория призвана объяснить, какие силы действуют между атомами, как атомы объединяются в молекулы, что обеспечивает устойчивость образовавшейся сложной частицы (то же относится к кристаллам, жидкостям и другим телам).

2) Теория должна объяснить опытные факты, лежащие в основе классического понятия валентности, и наряду с этим существование и устойчивость многочисленных соединений, не укладывающихся в привычные рамки классических структурно-химических представлений.

3) Теория должна разработать единые методы расчета молекулярных параметров, интерпретировать молекулярные спектры.

4) Наконец, теория должна сделать возможным априорный расчет скорости химического процесса, зависимости ее от строения молекул реагирующих веществ.

Современная теория химической связи, теория строения молекул и кристаллов базируется на квантовой механике: молекулы, как и атомы, построены из ядер и электронов, и теория химической связи должна учитывать корпускулярно-волновой дуализм микрочастиц. До применения методов квантовой механики к химии не удавалось создать непротиворечивую теорию химической связи.

Её фундамент был заложен в 1927 г. Гейтлером и Лондоном. Выполнив на основе квантовой механики расчет свойств молекулы водорода, они показали, что природа химической связи электрическая, никаких особых сил химического взаимодействия не существует. Действующие в молекуле между ядрами и электронами гравитационные и магнитные силы пренебрежимо малы по сравнению с электрическими силами.

Квантовомеханический подход к исследованию строения атома и молекулы один и тот же: нужно составить и решить уравнение Шредингера для системы из электронов и ядер и дать физическую интерпретацию полученным решениям. Составляя уравнение Шрёдингера для электронной энергии молекулы в приближении Борна — Оппенгеймера, считают ядра неподвижными.

Следовательно, электронная энергия для молекулы не зависит от координат ядер, а только от фиксированного расстояния R между ними (рис. 6.2). Во внимание принимаются лишь изменения координат электронов. Простейшая из молекул молекулярный ион содержит один электрон и два ядра. Для одного электрона в поле двух ядер (ион ) уравнение Шредингера имеет вид

. (6.5)

Для молекулярного иона потенциальная энергия

(6.6)

включает притяжение электрона 1 к ядрам А и В (первые два члена) и отталкивание ядер (ядра А и В у совершенно одинаковы — это протоны). Для иона с учетом (6.6) уравнение Шредингера принимает вид

, (6.7)

где Ψ — одноэлектронная волновая функция (собственная функция Шредингера для системы с одним электроном). Индексы «эл. мол.» при E и Ψ — опущены для упрощения записи.

Состояние молекулы Н2 описывается уже двухэлектронной функцией Ψ, зависящей от координат двух электронов (см. рис. 6.2).

Многоэлектронными будут и волновые функции более сложных молекул. Уравнение Шредингера для молекулы Н2 имеет вид

(6.8)

Индексы 1 и 2 при операторах Лапласа указывают, что волновая функция молекулы дифференцируется по координатам первого () и второго () электронов. Усложнится и выражение для потенциальной энергии:

(6.9)

В (6.9) первые четыре члена обозначают потенциальную энергию притяжения электронов 1 и 2 к ядрам А и В соответственно, пятый член — потенциальную энергию взаимного отталкивания электронов 1 и 2, последний член — энергию отталкивания ядер. Аналогично записывается уравнение Шредингера и для многоатомных молекул. В уравнениях (6.7) и (6.8) используется координатная молекулярная функция Ψ. Полная волновая функция молекулы Фмол, учитывающая и спин, должна удовлетворять принципу Паули антисимметрии волновых функций и строится в виде определителя.

Для молекулы, так же как и для атома, точное решение уравнения Шредингера возможно лишь для системы, содержащей один электрон — для молекулярного иона типа . Уже для молекулы Н2 в выражении (6.9) появляется член (энергия электронного отталкивания), зависящий от координат двух электронов, и точное решение невозможно. Однако принципиальный ответ о природе химической связи можно получить и при помощи приближенных методов решения волнового уравнения.

§3. Вариационный метод решения уравнения Шрёдингера

Одним из широко применяемых при рассмотрении теории химической связи приближенных методов решения уравнения Шредингера является вариационный метод. Здесь коротко излагается его сущность.

Уравнение Шредингера (1.1) может быть представлено в так называемой операторной форме. Для этого разделим все члены уравнения на и перегруппируем члены. Получим

.

Сумма двух действий, производимых над функцией Ψ в левой части, дифференцирование и умножение, может быть записана с помощью оператора ,

который называют оператором энергии, оператором Гамильтона или гамильтонианом. Уравнение приобретает лаконичную форму:

По такому же принципу строится оператор Гамильтона для многоатомных систем, например, для молекулы Н2

(6.11)

Умножим обе части уравнения Шредингера (6.10) на функцию Ψ*, комплексно сопряженную с волновой функцией

. (6.12)

Если Ψ — действительная функция, то Ψ*=-Ψ. (Левую сторону уравнения (6.12) нельзя записать аналогично правой в виде , так как в отличие от E — оператор, а не число). Возьмем интеграл от обеих частей (5.12) по всему пространству, причем Е как постоянную величину вынесем за знак интеграла:

.

. (6.13)

Если функция Ψ нормирована, знаменатель обращается в единицу и

. (6.14)

Если известно точное выражение для Ψ, то энергия системы может быть рассчитана по формулам (6.13) или (6.14). Однако, обычно не известны ни Ψ ни Е либо неизвестна Ψ. Тогда для отыскания Ψ и Е можно воспользоваться вариационным принципом: подставив в (6.13) или (6.14) вместо истинной функции приближенную к ней так называемую пробную функцию Ψпробн, получим отвечающее ей значение Е. Оно обязательно будет не ниже энергии основного состояния системы E0

. (6.15)

Видео:Уравнение Бернулли для потока жидкостиСкачать

Закон сохранения энергии. Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2

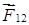
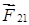
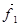
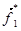
Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m₁ и m₂. Пусть частицы взаимодействуют друг с другом с силами и , модули которых зависят от расстояния R₁₂ между частицами. Установлено, что такие силы являются консервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная сила и внешняя неконсервативная сила . Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:

Умножим каждое уравнение на 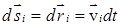и сложим полученные выражения.

1. Распишем первый член в правой части.

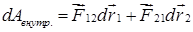
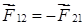
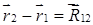
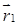
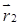
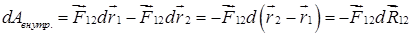
Работа внутренних сил равна . Для замкнутой системы , а , где и – радиус-векторы частиц.

.

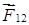
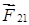
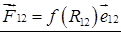
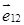
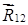
Учитывая, что силы и имеют величину, зависящую только от расстояния и направлены вдоль соединяющей их прямой (это справедливо, например, для сил кулоновского или гравитационного взаимодействий), любую из этих сил можно представить в виде, например, , где f(R₁₂) – некоторая функция R₁₂, – орт вектора .

Следовательно, .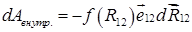

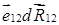
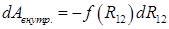
Скалярное произведение равно приращению dR₁₂ расстояния между частицами, тогда .

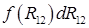
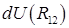
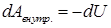
Выражение есть приращение некоторой функции . Следовательно,

.

Функция 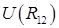представляет потенциальную энергию взаимодействия.

Работа внутренних сил будет равна

,

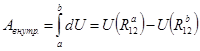
т.е. не зависит от пути, по которому перемещаются частицы, а определяется начальной и конечной конфигурациями системы. Т.е. силы взаимодействия вида 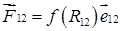являются консервативными.

Итак, работа внутренних сил равна убыли потенциальной энергии взаимодействия

2. Второй член представляет работу внешних сил и равен убыли потенциальной энергии системы во внешнем поле консервативных сил

3. Последний член представляет работу неконсервативных внешних сил .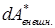

После этих замечаний можно записать

– называется полной механической энергией системы. Если внешние неконсервативные силы отсутствуют, т.е. 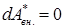, то

Е=const – закон сохранения механической энергии.

ОПРЕДЕЛЕНИЕ: полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной.

Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, закон сохранения примет вид:

E = T + U_вз. = const

Если в замкнутой системе, кроме консервативных сил действуют неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется. Рассматривая консервативные силы как внешние, получим

или после интегрирования .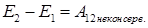

Как правило, силы трения совершают отрицательную работу. Поэтому наличие сил трения в замкнутой системе приводит к уменьшению ее полной механической энергии со временем. Таким образом, если в системе действуют неконсервативные силы, то
	изменение полной энергии будет равно работе всех внешних сил, действующих на эту систему.

Анализ закона сохранения показывает, что полная энергия, оставаясь в консервативной системе величиной постоянной, может переходить из одних видов в другие.

При действии неконсервативных сил возможен переход механической энергии в другие немеханические виды энергии. В этом случае справедлив более общий закон сохранения:

ОПРЕДЕЛЕНИЕ: в изолированной от любых внешних воздействий системе остается постоянной сумма всех видов энергии (включая и немеханические).

К этому добавим, что в природе и технике постоянно имеют место превращения энергии из одних видов в другие. Проиллюстрируем это таблицей.

В таблице не отражено, что при любом превращении часть энергии превращается в теплоту.

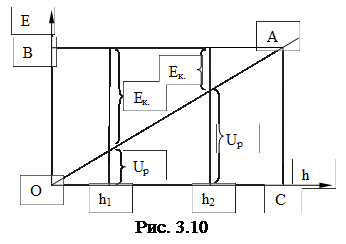
Для графического изображения закона сохранения энергии рассмотрим случай, когда тело бросаем вверх.

Если не учитывать силу сопротивления воздуха F_сопр., то систему «тело-Земля» можно рассматривать, как изолированную и консервативную, для которой

Из графика (рис. 3.10) видно, что по мере поднятия тела над поверхностью Земли его потенциальная энергия возрастает от величины U_p(h₁) до U_p(h₂), но одновременно с этим точно на такую же величину уменьшается кинетическая энергия системы E_к., а полная энергия тела остается величиной постоянной, что соответствует линии BA || h.

1. При h=0 имеем U_p=0, а E=E_к., что соответствует линии ОВ;

2. При h = max имеем U_p = max (E_к. = 0), а E = U_p, что соответствует линии AC.

Упругий и неупругий центральный удар шаров;

Видео:Уравнение БернуллиСкачать

Энергия

1.77. Найти приращение энергии ΔE, если: а) Е₁=2 Дж, E₂=5 Дж, б) E₁=10 Дж, E₂=8 Дж.

1.78. Для указанных в задаче 1.77 начальной Е₁ и конечной Е₂ энергий найти убыль энергии -ΔE.

1.79. Первоначально покоившаяся частица, находясь под действием силы F=1e_x+2e_y+3e_z (Н), переместилась из точки (2, 4, 6) (м) в точку (3, 6, 9) (м). Найти кинетическую энергию T частицы в конечной точке.

1.80. Находясь под действием постоянной силы с компонентами (3, 10, 8) (Н), частица переместилась из точки 1 с координатами (1, 2, 3) (м) в точку 2 с координатами (3, 2, 1) (м). Определить: а) Какая при этом совершается работа А? б) Как изменилась кинетическая энергия частицы?

1.81. Доказать соотношение: T_л = T_ц + mV_C 2 /2, где T_л — кинетическая энергия системы материальных точек, определяемая в лабораторной системе отсчета (л-системе), T_ц — кинетическая энергия, определяемая в системе центра масс (ц-системе), m — суммарная масса системы, V_C — скорость центра масс в л-системе.

1.82. Потенциальная энергия частицы в некотором силовом поле определяется выражением U=1,00x+2,00y 2 +3,00z 3 (U в Дж, координаты в м). Найти работу А, совершаемую над частицей силами поля при переходе из точки с координатами (1,00; 1,00; 1,00) в точку с координатами (2,00; 2,00; 2,00).

1.83. Потенциальная энергия частицы определяется выражением U=a(x 2 +y 2 +z 2 ), где a — положительная константа. Частица начинает двигаться из точки с координатами (3,00; 3,00; 3,00) (м). Найти ее кинетическую энергию T в момент, когда частица находится в точке с координатами (1,00; 1,00; 1,00) (м).

1.84. Два тела соскальзывают без трения и без начальной скорости с наклонных плоскостей 1 и 2 (рис. 1.12). а) Сравнить скорости тел v₁ и v₂ в конце соскальзывания. б) Одинаковы ли времена соскальзывания t₁ и t₂?

1.85. Имеются две наклонные плоскости, совпадающие с хордами одной и той же окружности радиуса R (рис. 1.13). С каждой из них соскальзывает без трения и без начальной скорости небольшое тело. Для какой из плоскостей время соскальзывания больше?

1.86. Небольшое тело массы m устанавливают в верхней точке наклонной плоскости высоты h и сообщают ему начальную скорость v₀, в результате чего оно начинает сползать по плоскости вниз (рис. 1.14). Поверхность плоскости неоднородна, поэтому скорость сползания изменяется некоторым произвольным образом. Однако в нижней точке плоскости скорость имеет первоначальное значение v₀. Какую работу А совершают силы трения на всем пути движения тела?

1.87. Небольшое тело начинает скользить без трения с вершины сферы радиуса R вниз (рис. 1.15). На какой высоте h над центром сферы тело отделится от поверхности сферы и полетит свободно?

1.88. По желобу, имеющему форму, показанную на рис. 1.16 (горизонтальный участок желоба сдвинут относительно наклонного в направлении, перпендикулярном к рисунку), с высоты h начинает скользить без трения небольшое тело (материальная точка). а) При каком минимальном значении высоты h тело опишет полную петлю, не отделяясь от желоба? б) Чему равна при таком значении h сила F давления тела на желоб в точке A?

1.89. Градиент скалярной функции φ в некоторой точке P представляет собой вектор, направление которого совпадает с направлением l, вдоль которого функция φ, возрастая по величине, изменяется в точке P с наибольшей скоростью. Модуль этого вектора равен значению dφ/dl в точке P. Аналитически это можно записать следующим образом: ∇φ = (dφ/dl)e_l. 1. Исходя из этого определения, найти выражения для: а) ∇r, б) ∇(1/r), в) ∇f(r), где r — модуль радиус-вектора точки P. 2. Убедиться в том, что такие же выражения получаются с помощью формулы: ∇φ = (∂φ/∂x)e_x + (∂φ/∂y)e_y + (∂φ/∂z)e_z.

1.90. Потенциальная энергия частицы имеет вид: a) U=α/r, б) U=kr 2 /2, где r — модуль радиус-вектора r частицы; α и k — константы (k>0). Найти силу F, действующую на частицу, и работу А, совершаемую над частицей при переходе ее из точки (1, 2, 3) в точку (2, 3, 4).

1.91. Потенциальная энергия частицы имеет вид U = a (x/y — y/z), где a — константа. Найти: а) силу F, действующую на частицу, б) работу А, совершаемую над частицей силами поля при переходе частицы из точки (1, 1, 1) в точку (2, 2, 3)

1.92. Потенциальная энергия частицы, находящейся в центрально-симметричном силовом поле, имеет вид U = a/r 3 — b/r 2 , где a и b — положительные константы. а) Имеется ли у этой частицы положение устойчивого равновесия по отношению к смещениям в радиальном направлении? б) Нарисовать примерную кривую зависимости U от r.

1.93. Частица движется по окружности в поле центральной силы, обратно пропорциональной квадрату расстояния от силового центра. В каком соотношении находятся в этом случае кинетическая T, потенциальная U и полная Е энергии частицы?

1.94. Частица массы m находится в силовом поле вида F=-(α/r 2 )e_r (α — положительная константа, r — модуль, а e_r — орт радиус-вектора частицы). Частицу поместили в точку с радиус-вектором r₀ и сообщили ей начальную скорость v₀, перпендикулярную к r₀. По какой траектории будет двигаться частица?

1.95. При каком условии траекторией частицы из предыдущей задачи будет окружность?

1.96. Невесомая нерастяжимая нить может скользить без трения по изогнутому желобу (рис. 1.17). К концам нити прикреплены грузы массами m₁=3,00 кг и m₂=1,00 кг. Груз массы m₁ поднимают настолько, чтобы груз массы m₂ коснулся пола, и отпускают. Высота h₁=1,00 м. На какую высоту h₂ над полом поднимется груз массы m₂ после того, как груз массы m₁ ударится о пол?

1.97. Автомобиль массы m=1,00 т ехал некоторое время по горизонтальному участку дороги с постоянной скоростью v=80 км/ч. При въезде на подъем, образующий с горизонтом угол α=10,0°, для того чтобы сохранить прежнюю скорость, пришлось, «прибавив газ», увеличить вращающий момент, приложенный к ведущим колесам, в η=6,20 раза. Считая силу F сопротивления воздуха движению автомобиля пропорциональной квадрату скорости, определить коэффициент k в формуле F=kv 2 . Трением в шинах пренебречь.

1.98. По резиновому шнуру, подвешенному одним концом к кронштейну (рис. 1.18), может скользить с независящим от скорости трением муфта массы m = 0,300 кг. Трение характеризуется силой F = 0,294 Н. Длина недеформированного шнура l₀=1,00 м, коэффициент пропорциональности между упругой силой и удлинением шнура k = 560 Н/м. На нижнем конце шнура имеется упор. Муфту поднимают в крайнее верхнее положение и отпускают. Пренебрегая внутренним трением в шнуре, размерами муфты, а также массами шнура и упора, определить: а) удлинение шнура Δl в момент достижения муфтой упора, б) скорость муфты v в этот момент, в) максимальное удлинение шнура Δl_max.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

🎬 Видео

Задача на теорему об изменении кинетической энергииСкачать

Урок 86 (осн). Энергия. Превращения энергииСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Урок 118. Потенциальная энергия гравитационного взаимодействия. Вторая космическая скоростьСкачать

Теорема об изменении кинетической энергии. Авторы: Малкова Полина, Петрашова ПолинаСкачать

Лекция 1 (вторая часть)Скачать

Физика 11 класс (Урок№2 - Механические волны.)Скачать

50 САМЫХ ГЕНИАЛЬНЫХ ТЕОРИЙ.Скачать

Закон Бернулли и движение по инерцииСкачать

ЛЕКЦИЯ №13 || Химическая кинетика || Конфигурационное пространство Поверхность потенциальной энергииСкачать

Физика с нуля: О чем ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ — Самое простое и понятное объясненияСкачать

Закон всемирного тяготенияСкачать

Как устроен квантовый мир / Эмиль Ахмедов в Рубке ПостНаукиСкачать

ВСЕ ТЕОРИИ ПРОИСХОЖДЕНИЯ ВСЕЛЕННОЙ ИЛИ ИНФЛЯЦИОННАЯ ВСЕЛЕННАЯ.Скачать

Тема 3. Пружинный и математический маятники. Превращения энергии при гармонических колебанияхСкачать

Общая физика | Л23: Элементы теории волн. Волновое уравнение. Поперечные и продольные колебанияСкачать