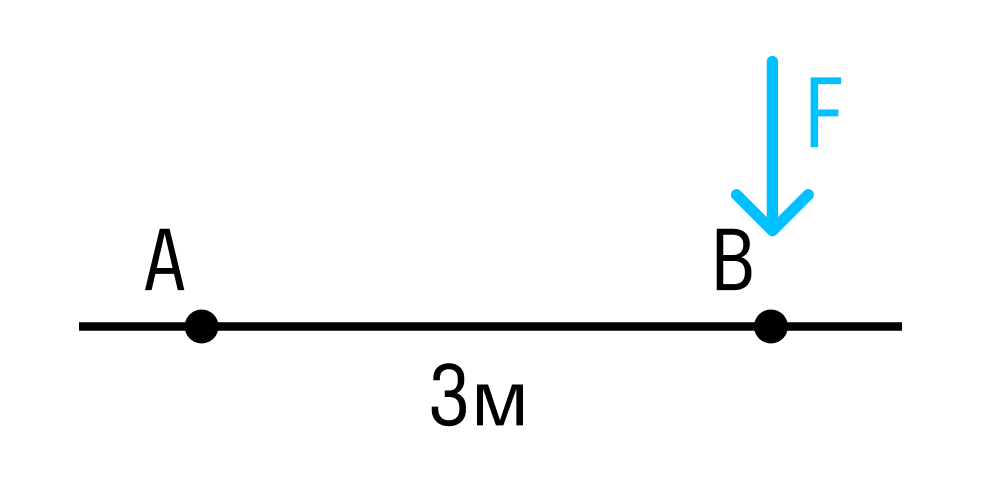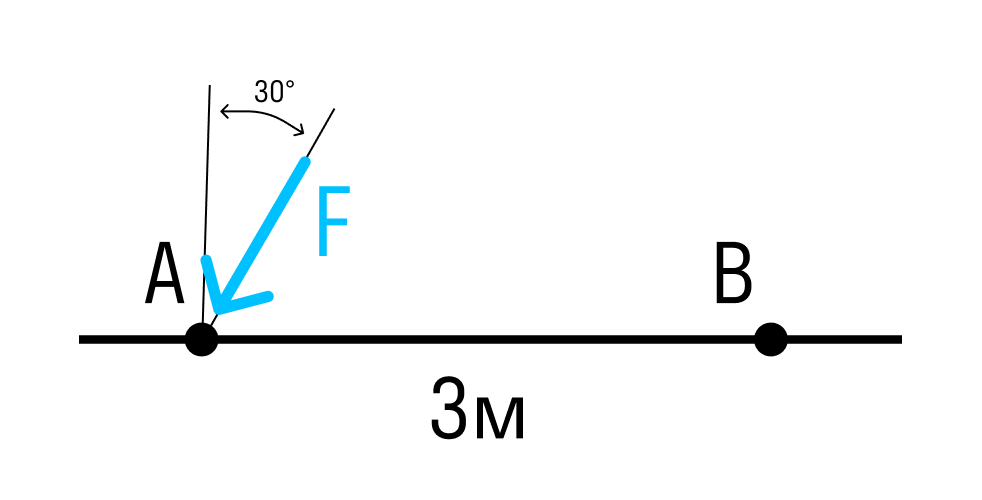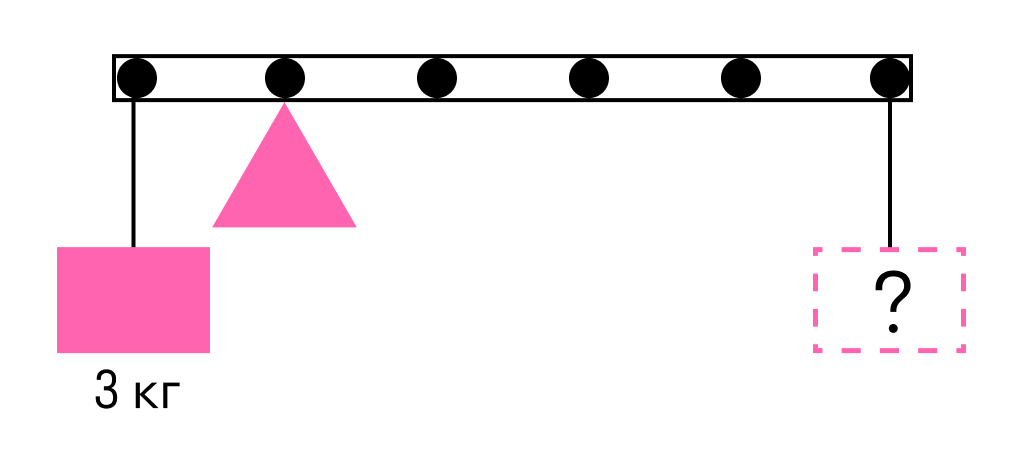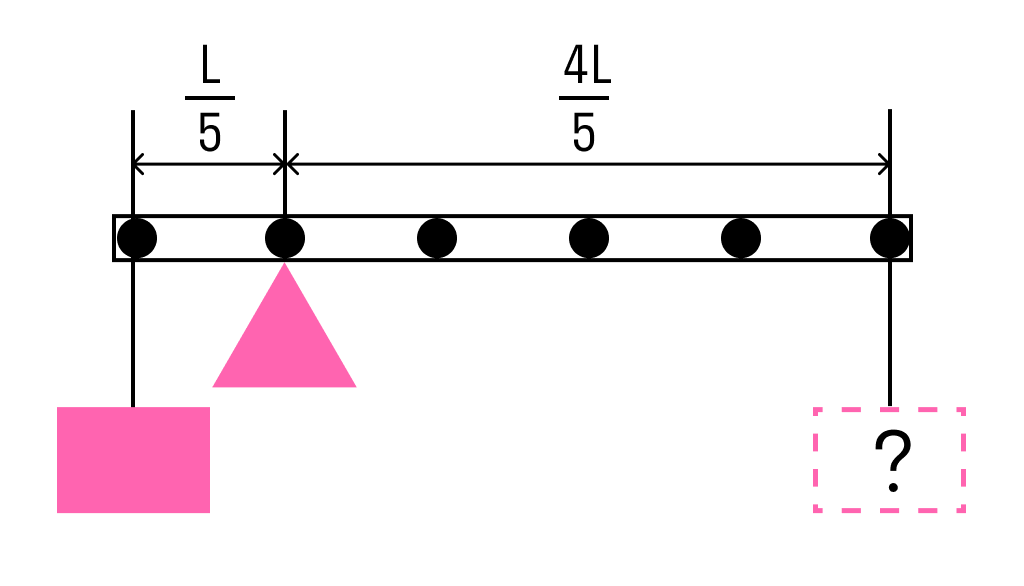Уравнение моментов сил 7 класс

О чем эта статья:

Видео:Момент силы. Видеоурок по физике 7 классСкачать

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

• Сила — это физическая векторная величина, является мерой действия тела на другое тело.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Правило равновесия рычага

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

F₁, F₂ — силы, действующие на рычаг

Видео:Сила. 7 класс.Скачать

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы

M = Fl

M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]

Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.

Для начала приложим силу к краю двери — туда, где самый длинный рычаг. Открылась!

А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.

Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.

Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Расчет момента силы

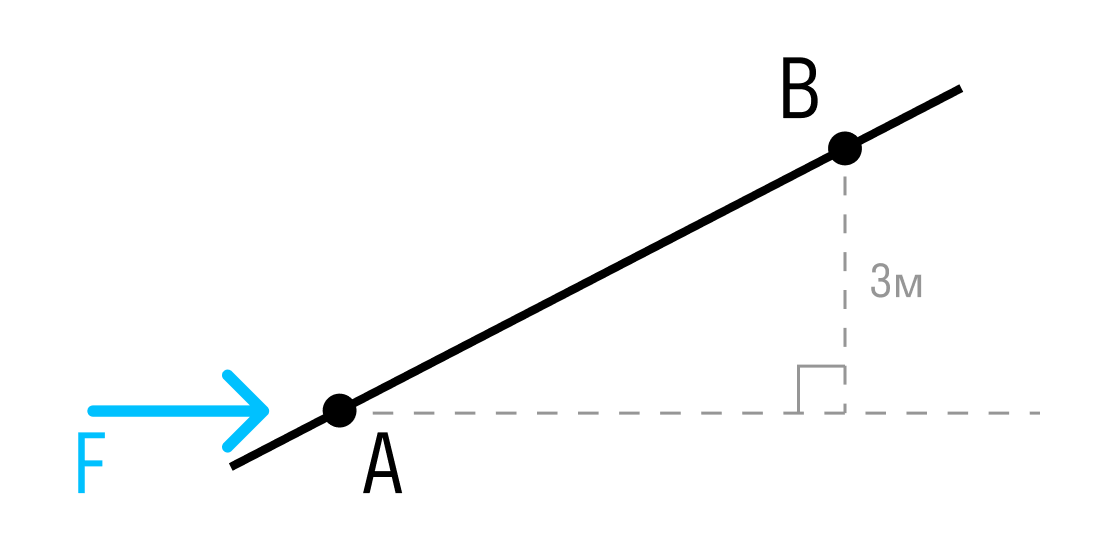
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

Видео:7 класс Момент силыСкачать

Правило моментов

Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов

M₁ + M₂ +. + M_n — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]

M’₁ + M’₂ +. + M’_n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м]

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом: — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой

M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага:

где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

Ответ: расстояние ОА равно 30 см

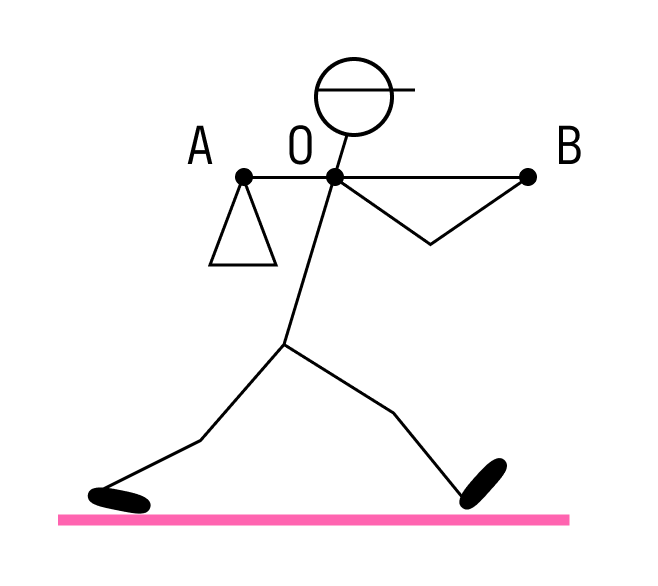
Задача 3

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага

Ответ: Масса груза равна 0,3 кг

Задача 4 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Видео:Момент силыСкачать

Момент силы

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Содержание

Поговаривают, что древнейшим открытием и в какой-то степени самым первым научным достижением человека можно смело называть рычаг. Удивительно, но наши предки на уровне интуиции понимали, что увесистый камень намного проще поднять или передвинуть с помощью самой обычной палки, — при этом удивляет больше не наличие палки во всей этой истории, а осознание первобытным человеком принципа простых механизмов. Ведь палки первые разумные жители планеты специально искали подлиннее, понимая: чем длиннее, тем мне будет проще совершить работу.

«Катить проще, чем тянуть» — еще одно древнейшее «научное» открытие примитивного человека наряду с рычагом.

Принцип рычага передавался из уст в уста, от одного племени к другому, от одного поколения к следующему, словно элемент фольклора. Мы не знали, почему это работает, какое отношение к этому имеет наука физика. Более того, мы и слова-то такого не знали — «физика». У нас не было формул, не было определений, не было следствий из этих определений. Был лишь рычаг в самых его разных формах проявления и четкое знание — возьмись подальше от точки опоры, если тяжело.

И лишь в третьем веке до нашей эры, к моменту, когда рычаговые механизмы успели стать прочной основой нашей жизнедеятельности, Архимед впервые произвел необходимые математические расчеты и наконец описал теорию рычага, которой мы пользуемся и по сей день. Он первым связал друг с другом понятия груза, плеча и силы, и, как гласит легенда, осознав масштабы своего открытия, воскликнул: «Дайте мне точку опоры, и я переверну Землю!»

Благодаря опытам Архимеда, его фундаментальному пониманию закона равновесия рычага, впоследствии возникла крайне важная физическая величина — момент силы.

Видео:Урок 76. Задачи на правило моментовСкачать

Закон равновесия: опыт с грузами

Определить момент силы можно как следствие закона сохранения энергии, как следствие второго закона Ньютона, также можно определить его методами векторной алгебры, однако чтобы не просто определить, но понять, что скрывается за данной величиной, не нужно применять пока нам незнакомые понятия — достаточно вспомнить условие равновесия рычага и провести несложный опыт с подвешенными грузами.

Опыт с грузами, рис. 1. Простая система из линейки, балки, крепления и крючков.

Во-первых, возьмем небольшую деревянную балку и к ее верхнему концу прикрепим болтом мерную линейку таким образом, чтобы крепление располагалось в центре тяжести линейки. Далее к линейке прикрепим по сантиметровым делениям несколько крючков, за которые будем подвешивать грузики разной массы. Начнем с отметок $10$ и $20$ — по пять сантиметровых делений влево и вправо от центра тяжести в $15

Опыт с грузами, рис. 2. Справа от точки опоры рычага подвешиваем первый грузик массой $20

Теперь возьмем грузик массой $40

г$ и для примера так же подвесим его за крючок, располагающийся на расстоянии $5

см$, только с другой стороны. Очевидно, что рычаг в результате не окажется в положении равновесия: с левой стороны, где висит сорокаграммовый грузик, на плечо рычага действует бó‎льшая сила $mvec$.

Опыт с грузами, рис. 3. Отклонение рычага в левую сторону при подвешивании второго грузика массой $40

Интуитивно мы понимаем, что дабы добиться равновесия данной системы, один из грузиков нужно куда-то сместить. Мы так же интуитивно понимаем, что если смещать грузик массой $40

г$, его нужно подвесить за крючок, располагающийся ближе к точке опоры. Смещать грузик массой $20

г$ нужно в другую сторону — подальше от точки опоры.

Вопрос на миллион: если, скажем, мы хотим перевесить двадцатиграммовый грузик, на сколько делений должно увеличиться плечо груза?

Опыт с грузами, рис. 4. Рычаг в положении равновесия.

Стандартным методом проб и ошибок, перевешивая крючок с грузиком по разным отметкам на линейке, можно со временем обнаружить, что рычаг придет в положение равновесия, если двадцатиграммовый грузик подвесить на расстоянии десяти сантиметров от точки опоры — на отметке $25

см$. Обратите внимание на то, как пропорциональны получаемые величины: грузики массой $40

г$ уравновешивают друг друга на плечах длиной $5

Видео:Сложение сил, действующих на тело вдоль одной прямой. 7 класс.Скачать

Условие равновесия

Именно таким образом, исключительно эмпирически, то есть опытным путем, Архимедом было сформулировано условие равновесия рычага. Можно долго перевешивать грузики, пользоваться различными массами, рычагами короткими, рычагами длинными, но одна вещь всегда будет объединять все элементы и переменные:

Рычаг находится в положении равновесия при условии, что отношение масс, подвешенных грузов, будет обратно пропорционально отношению расстояний от точки опоры до центров тяжести грузов.

Математически записать можно следующим образом:

где $m_1$ — масса первого груза, $m_2$ — масса второго груза, $l_2$ — расстояние от точки опоры до центра тяжести второго груза, $l_1$ — расстояние от точки опоры до центра тяжести первого груза.

Однако подобное определение, как и полученная нами формула, годится разве что для физики уровня III век до н. э. Масса — понятие не универсальное, «расстояние от точки опоры до центра тяжести» звучит размыто и в ряде неочевидных по устройству рычаговых систем может вызывать больше вопросов, чем ответов. Что, если мы хотим дополнительно надавить на грузик? Как учесть это в формуле? А что, если под рычагом мы понимаем гаечный ключ? К нему прикладывается сила. Считать, сколько килограммов человек прилагает к ключу, чтобы он пришел в движение? Да уж: ненаучно, странно и расплывчато.

Если от масс перейти к силам, чтобы внести универсальности, и учесть, что на подвешенные грузики действует только одна сила — сила тяжести $mvec$, а вместо расстояний взять уже знакомое нам определение, связанное с силой — плечо силы, формулу можно улучшить до следующего вида:

Лучше, но все равно не то. Где гарантии, что на наш абстрактный грузик будет действовать только сила тяжести? Возвращаясь к вопросу о том, что на грузик можно надавить, причем не обязательно параллельно направлению вектора силы тяжести — сделать это можно под углом. Формула равновесия должна учитывать силы в общем и целом. Так что улучшим пропорцию еще раз и придем к окончательному математическому выражению условия равновесия:

где $F_1$ и $F_2$ — силы, действующие на рычаг, $l_1$ и $l_2$ — плечи сил.

Рычаг находится в положении равновесия, когда отношение сил, действующих на рычаг, обратно пропорционально отношению плеч этих сил.

Вот это уже определение универсальное: оно охватывает и наш частный случай с силой тяжести, и более комплексные системы в том числе. А теперь заметим, что согласно основному свойству пропорции из формулы выше получается следующее равенство:

$$F_1cdot l_1 = F_2cdot l_2$$

Ранее мы с подобным не сталкивались — с произведением силы на плечо силы. Именно это произведение и именуется в физике моментом силы.

Видео:Физика 7 класс (Урок№13 - Равнодействующая сила.)Скачать

Определение момента силы

Формально момент силы определяется так:

Момент силы — физическая величина, характеризующая действие силы. Равняется произведению модуля силы на ее плечо.

В физике момент силы обозначается заглавной латинской литерой $M$ и измеряется в $Н cdot м$ — в ньютонах на метр. Характеризует момент силы, как мы указали в определении, действие силы. Но только что бы это могло значить и как бы это можно было понять?

Рисунок 5. Опыт с гаечным ключом. Обратите внимание на направление момента силы $M$.

Возьмем гаечный ключ, ухватимся рукой за его конец и приложим некоторое усилие, чтобы провернуть гайку. Для сравнения перехватим гаечный ключ примерно до середины ручки и также попробуем приложить некоторое усилие. Во втором случае провернуть гайку будет сложнее, чем если бы мы держались за конец ручки инструмента.

Причина? Образуются разные величины момента силы!

И это все то же самое о том же самом. То, о чем мы рассуждали, когда затрагивали принцип простых механизмов, отдельно рычагов; когда говорили о механическом выигрыше. Просто мы не могли дать строгого определения происходящему. Выходит, что «проще выполнить работу», «затратить меньше усилий», «взяться подальше» и прочие относительно абстрактные фразы, которые мы использовали при рассмотрении простых механизмов, расшифровываются следующим образом: образуется бóльший момент силы.

Иными словами, момент силы — это и есть в своем роде величина усилия. Чем больше момент, тем быстрее двигается предмет, тем проще он проворачивается, тем легче выполняется действие. Говоря языком аналогий, плечо силы можно представить взлетной полосой, а момент силы — скоростью самолета. Если полоса длинная, самолет сможет развить бóльшую скорость и легко, как следствие, оторваться от земли.

Так что, да, момент и вправду характеризует действие силы. Характеризует, насколько это действие, скажем, активное, энергичное, полезное для нас в достижении некоего результата. Ведь сила по модулю может быть одинаковая, но за счет «разных длин взлетных полос», то есть плеч сил, она может образовывать разный момент.

Больше момента силы — проще, быстрее, легче, механически выгоднее.

Видео:РЫЧАГ МОМЕНТ СИЛЫ физика 7 класс ПерышкинСкачать

Как рассчитать момент силы

Момент силы всегда рассчитывается как произведение модуля силы на плечо силы по записанной нами ранее формуле $M = F cdot l$. Иногда определять приходится результирующий момент — когда на тело действует несколько разнонаправленных сил, однако подобные «превратности» нам встретятся в программе лишь через пару лет, когда мы начнем более основательно использовать понятие вектора. Единственная сложность, которая пока может встретиться на пути, — определение плеча силы.

Для примера возьмем нечто отвлеченное от привычных нам двуплечих рычагов — ясно, что внутри подобной механической системы плечо силы чаще всего будет совпадать с плечом рычага, так что сложности как таковой с расчетом плеча силы не возникнет. Представим вместо этого, что мы раскручиваем прикрепленную к поверхности фигуру в форме трапеции. Ого!

Итак, наша вращающаяся трапеция. Силу мы прикладываем к концу фигуры — направление силы указано на изображении. Согласитесь, увидеть плечо силы для подобной схемы движения уже не так просто, особенно когда глаз привык к рычагам. Не паникуем и вспоминаем, что плечо силы есть перпендикуляр к линии действия силы, опущенный из точки опоры или, вернее сказать, из оси вращения. Подумайте, где на изображении находится ось вращения и по какой траектории проходит перпендикуляр.

Ответ: плечо силы будет равно длине отрезка $OA$. Ось вращения трапеции находится в точке $О$. Все гениальное просто, согласны?

Видео:Рычаг, момент силы. Физика 7 классСкачать

Знак момента силы

Еще один немаловажный момент при расчете момента силы — знак величины. Момент может быть отрицательным или положительным, в зависимости от того, в каком направлении действует сила, приложенная к телу. Если она вращает тело по часовой стрелке, то момент силы считается положительным. Если наоборот — против часовой стрелки, то момент считается отрицательным.

Может ли момент быть нулевым? Конечно, почему нет. Логично предположить, что в случае, если плечо силы равно нулю, то сила не создает никакого момента. Например, если вы надавите на ось вращения, сдвинуть при таком приложении силы что-либо невозможно.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Решение задачи на моменты

На данном этапе мы понимаем, что такое момент силы, как определять плечо силы и что момент, в зависимости от направления движения, может иметь отрицательное значение. С учетом главной формулы $M = F cdot l$ решим следующую задачу.

Условие. На земле лежит палка массой 20 кг и длиной 4 м. Палку приподнимают за конец, прикладывая усилие 120 Н. Какие моменты при этом создают силы, действующие на доску? Для простоты допустить, что моменты силы тяжести в поднятом положении палки и в вертикальном положении к земле равны.

Решение. Выполним следующие действия:

• Схематично зарисуем условия.
• Определим силы, действующие на доску.
• Определим ось вращения.
• Определим плечи сил.
• Рассчитаем моменты.

На палку действуют три силы: сила реакции опоры $vec$, сила тяжести $mvec$ и внешняя сила, которую мы прикладываем к концу, $vec$. Расположение сил и их направление изображено на рисунке. Ось вращения при этом располагается в точке $B$: мысленно представим, что палка совершает вращательное движение, описывает полный круг, а так как точка $B$ будет находиться в центре полученной окружности, она и будет считаться осью вращения.

Плечо силы реакции опоры $vec$ равно нулю, поскольку точка приложения силы и ось вращения совпадают. Следовательно, первый момент $M_N$ силы реакции опоры мы можем определить сразу без расчетов. Он равен нулю:

Далее опускаем перпендикуляр из оси вращения $B$ к внешней силе $vec$. Получаем, что плечо внешней силы $vec$ равно длине палки $d$:

По формуле $M = F cdot l$, зная, что по условию задачи длина палки составляет $4

м$, а модуль внешней силы равен $120

Н$, рассчитаем момент внешней силы $M_F$. Вращение происходит по часовой стрелке, следовательно, момент будет положительным по знаку.

Если допустить, что момент силы тяжести $M_$ в поднятом положении палки равен моменту в вертикальном положении к земле, то плечо силы тяжести $l_$ равно половине длины палки:

Примечание. Подобное допущение необходимо исключительно для простоты расчетов. Если бы пришлось определять плечо силы тяжести «честно», в задаче также должны фигурировать как минимум высота подъема палки и угол подъема. Для вычисления плеча в треугольнике понадобились бы теорема косинусов и геометрические признаки подобия треугольников. Да-да, это вообще что за термины такие? Поэтому считаем «нечестно», в лежачем положении. Нахождением сложных плеч вы будете заниматься в курсе статики для 10 класса.

Теперь рассчитаем момент силы тяжести $M_$ по формуле моментов, учитывая, что движение происходит против часовой стрелки. Момент отрицательный:

$$M_=-fraccdot mgcdot l_=-0.5 cdot 20 cdot 9.8 cdot 2 =-196

Ответ: $M_N=0, M_F=480

Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Правило моментов

Остается последнее — разобраться, зачем нужно отрицательное значение момента силы.

Ранее мы говорили о том, что условием равновесия рычага является обратная пропорциональность отношений сил к плечам этих сил. Однако условие равновесия можно задать и через смежное понятие момента силы, что в некоторых случаях даже удобнее для вычислений.

Вернемся к нашей вращающейся трапеции. Представим, что вы стоите и прикладываете к одному концу трапеции силу $vec_1$, а внезапно появившийся из ниоткуда ваш друг увидел, как вы играетесь с фигуркой и решил тоже во всем этом поучаствовать. Он берется за другой конец трапеции и тянет фигурку в противоположную сторону c силой $vec_2$. Вы в одну сторону, он в другую, при этом трапеция вращаться никуда не хочет — она упрямо находится в положении равновесия. Но, казалось бы, моменты сил создаются. Где движение?

Дело в том, что один момент силы, условно говоря, «гасит» другой. Математически вычитается. Как только создаваемый вами момент силы превысит тот, что создается вашим другом, фигурка начнет движение по часовой стрелке, к вам. Если друг поднажмет, то трапеция пойдет против часовой стрелки, от вас.

Таким образом, мы можем складывать все моменты, действующие на тело, чтобы понимать, движется ли тело, и если да, то в какую сторону. Знак числа — удобный математический инструмент, позволяющий работать с направлениями. Если сумма всех моментов положительна, вращательное движение идет по часовой стрелке. Если отрицательна — против часовой.

А если сумма моментов равна нулю?

Логично, что тогда тело находится в положении равновесия. Оно не двигается. Вот как мы можем получить условие равновесия (неважно — рычага или другого тела), выраженное через момент силы.

$$sum_i M_i= M_1+M_2+…+M_i =0$$

Подобное равенство называется правилом моментов:

Правило моментов: тело находится в состоянии покоя, если алгебраическая сумма всех моментов сил, приложенных к телу, равняется нулю.

Видео:момент силы, 7 класс, 2022Скачать

Уравнение моментов сил 7 класс

Правило равновесия рычага:

1. Что называется моментом силы?

Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы и обозначается буквой М.

2. В чем состоит правило моментов?

Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.

Если силы, действующие на рычаг: 2 Н и 4 Н.
Их плечи соответственно составляют 4 и 2 деления рычага.
То моменты этих сил при равновесии рычага равны.

3. Что принимают за единицу момента силы?

Момент силы может быть измерен.

За единицу момента силы принимается момент силы в 1 Н, плечо которой равно 1 м.

Единица момента силы в системе СИ называется ньютон-метр (Н м).

Что показывает момент силы?

Момент силы характеризует действие силы и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча.

Действие силы на дверь зависит и от модуля силы, и от того, где приложена сила.
Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила.

Гайку легче отвернуть длинным гаечным ключом, чем коротким.

Ведро тем легче поднять из колодца, чем длиннее ручка ворота.

🎬 Видео

Момент силы. Рычаги в природе, технике, быту | Физика 7 класс #44 | ИнфоурокСкачать

7 класс, 8 урок, Сила. Равнодействующая силСкачать

Сложение двух сил, направленных по одной прямой | Физика 7 класс #22 | ИнфоурокСкачать

Урок 38 (осн). Сложение сил, направленных по одной прямой. РавнодействующаяСкачать