Уравнение моментов для частицы и системы частиц

Закон сохранения момента импульса >>

Уравнение моментов для частицы и системы частиц. dL/dt = M – скорость изменения момента импульса частицы равна моменту силы: dL/dt = [dr/dt,p] + [r,dp/dt] = [r,dp/dt] = [r,F] = M Для системы частиц: dL/dt = Mвнешн – производная по времени от момента импульса системы материальных точек относительно произвольного неподвижного начала равна суммарному моменту всех внешних сил относительно того же начала. dLz/dt = Mz – уравнение моментов относительно неподвижной оси 0Z. Если Mz = 0, то Lz = const.

Слайд 8 из презентации «Момент силы 10 класс»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Момент силы 10 класс.ppt» можно в zip-архиве размером 235 КБ.

Похожие презентации

«Вещества тела частицы» — Твёрдые жидкие газообразные СОЛЬ ВОДА ГАЗ. Любой предмет, любое живое существо можно назвать телом. Тела состоят из Веществ. Тела. Тела, вещества, частицы. Вещества состоят из мельчайших частиц, невидимых глазом. Загадки. Естественные Искусственные. Первый русский ученый – естествоиспытатель, физик, химик, историк, поэт и художник.

«Частица 7 класс» — Частица как часть речи. Правописание частиц. Проблемные вопросы. Создать ситуацию успеха на уроке. Основополагающий вопрос. Представление результатов исследования. Уметь определять роль частиц в предложении. Что такое ЧАСТИЦА. Какие разряды частиц бывают? Зачем нужны части речи? Употребление и разграничение на письме частиц НЕ и НИ.

«Методы наблюдения и регистрации частиц» — Анод. Вильсон Чарлз Томсон Рис. « ….. воспитание творческих способностей в человеке основывается на развитии самостоятельного мышления» П.П. Капица. Пузырьковая камера. Стеклянная трубка. Методы наблюдения и регистрации элементарных частиц. Газоразрядный счётчик Гейгера. Сцинтилляционный метод. Регистрация сложных частиц затруднена.

«Методы регистрации элементарных частиц» — Пролёт частицы вызывает образование цепочки капель, которые можно сфотографировать. Счетчик Гейгера. Разрядные искры строго локализованы. Треки элементарных частиц в толстослойной фотоэмульсии. Расстояние между пластинами от 1-2 см до 10 см. Метод толстослойных фотоэмульсий. 20-е г.г. Л.В.Мысовский, А.П.Жданов.

«Заряжённые частицы» — Метод толстослойных фотоэмульсий позволяет регистрировать редкие явления. Пузырьковая камера. Метод толстослойных фотоэмульсий. Применение изотопов. Счётчик Гейгера позволяет регистрировать только факт пролета частицы. Изотопы. Счетчик Гейгера. Пузырьковая камера позволяет регистрировать траектории заряженных частиц.

«Момент силы» — Тема урока: «Момент силы». Задача. Сделайте расчет, пользуясь правилом моментов сил. Рычаги в технике, быту и природе.

Уравнение моментов: моменты силы, импульса и инерции

Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то характеристики движения механических систем по круговым траекториям вычисляют с помощью специального выражения, которое называется уравнением моментов. О каких моментах идет речь и в чем заключается смысл этого уравнения? Эти и другие вопросы раскрываются в статье.

Момент силы

Всем хорошо известна ньютоновская сила, которая, действуя на тело, приводит к сообщению ему ускорения. Когда же такая сила прилагается к объекту, который закреплен на некоторой оси вращения, то эту характеристику принято называть моментом силы. Уравнение момента силы может быть записано в следующем виде:

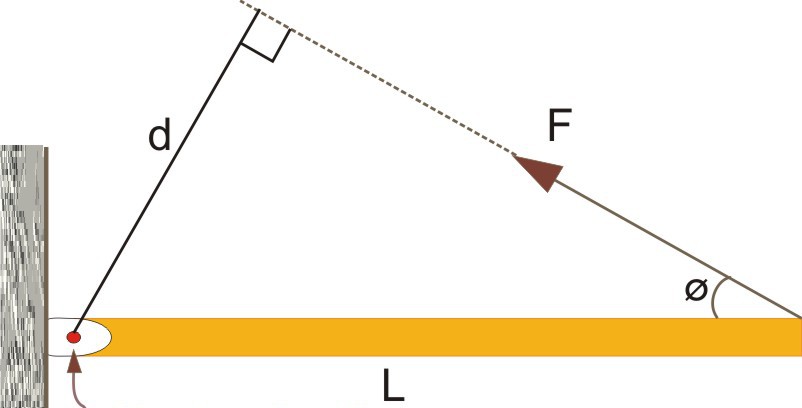
Рисунок, поясняющий это выражение, приведен ниже.

Здесь видно, что сила F¯ направлена к вектору L¯ под углом Φ. Сам же вектор L¯ полагается направленным от оси вращения (указана стрелкой) к точке приложения F¯.

Приведенная выше формула представляет собой произведение двух векторов, поэтому величина M¯ также является направленной. Куда будет повернут момент силы M¯? Это можно определить по правилу правой руки (четыре пальца направлены вдоль траектории от конца вектора L¯ к концу F¯, а отставленный палец большой показывает направление M¯).

На рисунке выше выражение для момента силы в скалярном виде примет форму:

Если внимательно всмотреться в рисунок, то можно увидеть, что L*sin(Φ) = d, тогда имеем формулу:

Величина d является важной характеристикой при вычислении момента силы, поскольку она отражает эффективность приложенной F к системе. Эту величину принято называть рычагом силы.

Физический смысл M заключается в способности силы совершить вращение системы. Эту способность может ощутить на себе каждый, если будет открывать дверь за ручку, толкая ее около петель, или же попробует открутить гайку коротким и длинным ключом.

Равновесие системы

Понятие о моменте силы оказывается очень полезным, когда рассматривают равновесие системы, на которую действуют несколько сил, и которая имеет ось или точку вращения. В таких случаях применяют формулу:

То есть система будет находиться в равновесии, если сумма всех моментов сил, приложенных к ней, нулевая. Заметим, что в этой формуле присутствует знак вектора над моментом, то есть при решении следует не забывать учитывать знак этой величины. Общепринятым правилом считается, что действующая сила, которая вращает систему против часовой стрелки, создает положительный M_i¯.

Ярким примером задач рассматриваемого типа являются проблемы с равновесием рычагов Архимеда.

Момент импульса

Это еще одна важная характеристика движения по окружности. В физике ее описывают произведением количества движения на рычаг. Уравнение момента импульса имеет такой вид:

Здесь p¯ — вектор импульса, r¯ — вектор, соединяющий вращающуюся материальную точку с осью.

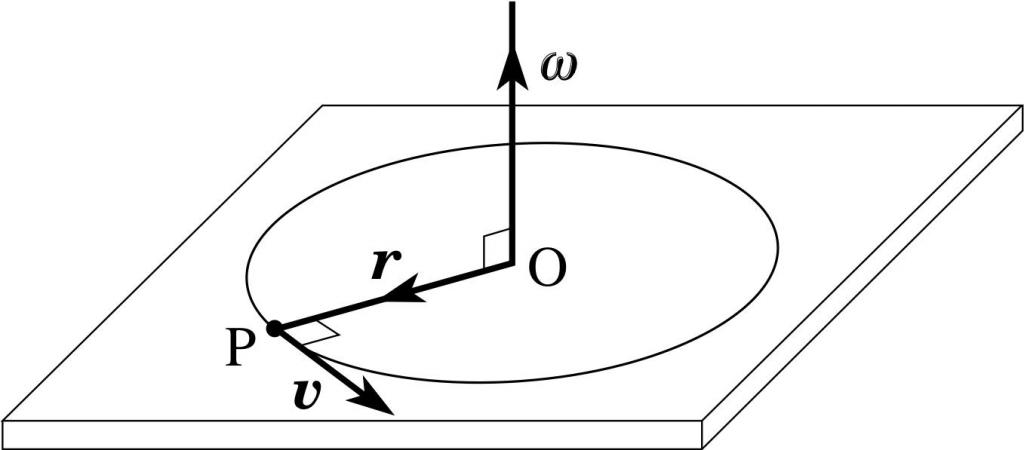
Поясняющий это выражение рисунок приведен ниже.

Здесь ω — угловая скорость, которая дальше появится в уравнении моментов. Заметим, что направление вектора T¯ находится по тому же правилу, что и M¯. На рисунке выше T¯ по направлению будет совпадать с вектором угловой скорости ω¯.

Физический смысл величины T¯ является таким же, как и характеристики p¯ в случае линейного движения, то есть момент импульса описывает количество вращательного движения (запасенную кинетическую энергию).

Момент инерции

Третья важная характеристика, без которой невозможно составить уравнение движения вращающегося объекта, — это момент инерции. Появляется он в физике в результате математических преобразований формулы для момента импульса материальной точки. Покажем, как это делается.

Представим величину T¯ в следующем виде:

T¯ = r¯*m*v¯, где p¯ = m*v¯

Пользуясь связью между угловой и линейной скоростями, можно переписать это выражение следующим образом:

T¯ = r¯*m*r¯*ω¯, где v¯ = r¯*ω¯

Последнее выражение запишем в виде:

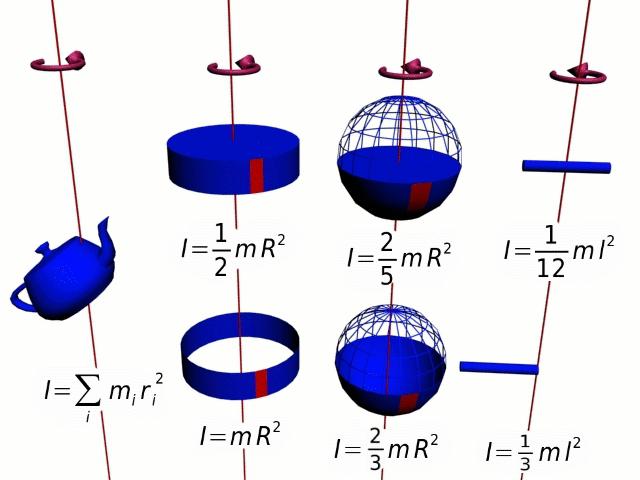
Величина r 2 *m — это момент инерции I для точки массой m, которая совершает круговое движение вокруг оси на расстоянии от нее r. Этот частный случай позволяет ввести общее уравнение момента инерции для тела произвольной формы:

I — это аддитивная величина, смысл которой заключается в инерционности вращающейся системы. Чем больше I, тем труднее раскрутить тело, и необходимо приложить значительные усилия, чтобы его остановить.

Уравнение моментов

Мы рассмотрели три величины, название которых начинается со слова «момент». Это сделано было намеренно, поскольку все они связаны в одно выражение, получившее название уравнения 3 моментов. Выведем его.

Рассмотрим выражение для момента импульса T¯:

Найдем, как изменяется величина T¯ во времени, имеем:

Учитывая, что производная угловой скорости равна таковой для скорости линейной, деленной на r, а также раскрывая величину I, приходим к выражению:

dT¯/dt = m*r 2 *1/r*dv¯/dt = r*m*a¯, где a¯ = dv¯/dt — линейное ускорение.

Заметим, что произведение массы на ускорение — это не что иное, как действующая внешняя сила F¯. В итоге получаем:

Мы пришли к интересному выводу: изменение момента импульса равно моменту действующей внешней силы. Это выражение принято записывать в несколько иной форме:

M¯ = I*α¯, где α¯ = dω¯/dt — угловое ускорение.

Это равенство называется уравнением моментов. Оно позволяет рассчитать любую характеристику вращающегося тела, зная параметры системы и величину внешнего воздействия на нее.

Закон сохранения T¯

Полученный в предыдущем пункте вывод свидетельствует о том, что если внешний момент сил будет равен нулю, то момент импульса меняться не будет. В таком случае запишем выражение:

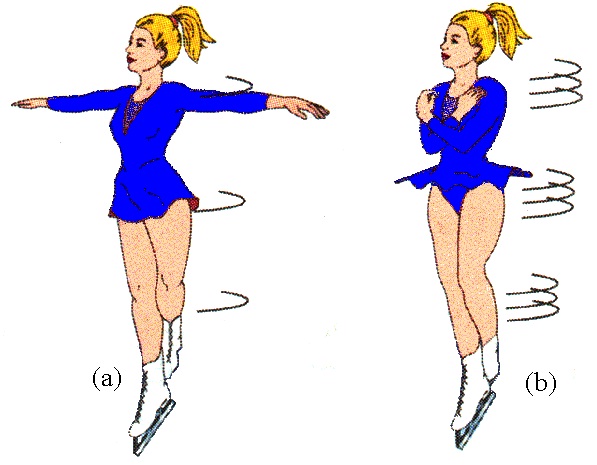
Эта формула носит название закона сохранения величины T¯. То есть любые изменения внутри системы суммарный момент импульса не меняют.

Этот факт используется фигуристами и балеринами во время их выступлений. Также его применяют, если необходимо выполнить поворот вокруг своей оси искусственного спутника, движущегося в космосе.

Уравнение моментов

Определение и уравнение моментов

Пусть O — любая неподвижная точка в инерциальной системе отсчета. Это называется началом или полюсом. Обозначим через радиус-вектор, взятый от этой точки до точки приложения силы (рис.1).

Момент силы относительно точки O является векторным произведением радиус-вектора и силы :

направление выбрано так, что последовательность векторов образует правую систему, т. е. если вы посмотрите вдоль вектора ,то поворот вдоль кратчайшего пути от первого фактора в (1) до вторая выполняется по часовой стрелке, таким образом совпадает с направлением поступательного движения правого штыря, ручка которого вращается от до вдоль кратчайшего пути.

Моментом нескольких сил относительно точки является векторная сумма моментов этих сил относительно одной и той же точки:

Момент импульса материальной точки

Момент импульса материальной точки относительно точки O является векторным произведением радиус-вектора и импульса

где J — момент инерции, — угловая скорость вращения тела.

Система из n материальных точек — это момент количества движения относительно некоторой точки O — векторная сумма моментов импульсов этих точек относительно того же начала:

Временная производная от момента импульса механической системы относительно неподвижной точки (полюса О) равна сумме внешних силовых моментов , действующих на систему:

Для материальной точки уравнение момента написано:

Уравнение (6) называется моментом для системы материальных точек. Это основной закон динамики твердого тела, вращающегося вокруг неподвижной точки.

В проекциях на оси фиксированной декартовой системы координат с началом на полюсе O уравнение моментов системы записывается в виде:

где — проекция момента количества движения на соответствующей оси; — проекции полного момента сил на соответствующую ось.

Уравнение моментов позволяет получить ответ на следующие вопросы:

1. найти момент силы (общий момент внешних сил) относительно интересующей нас точки в любой момент времени, если известна зависимость момента количества движения частицы (системы частиц) от одной и той же точки;

2. определить приращение углового момента частицы (системы частиц) относительно точки O для любого периода времени, если временная зависимость силового момента (полного момента внешних сил), действующего на эту частицу (система частиц) относительно одной и той же точки.

Примеры решения проблем

Сравните угловые скорости, полученные материальной точкой под действием крутящих моментов, графики (a, b) которых показаны на рисунках.

В соответствии с уравнением моментов для материальной точки мы имеем:

поскольку мы имеем дело с материальной точкой, соответственно, J не зависит от времени, получаем:

Вспомните геометрический смысл интеграла.

Вычислить и сравнить площадь треугольников OAB и OCD.

Области треугольников равны соответственно

Угловые скорости, полученные материальной точкой, равны в первом и втором случаях.

Горизонтальный диск с радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через ее центр. Зависимость угловой скорости вращения диска от времени определяется уравнением w = A + 8t. Найдите значение касательной силы, приложенной к ободу диска. Трение пренебрегалось.

Мы делаем рисунок

Запишем уравнение моментов:

где — искомая сила. Перепишите (2.2), найдите модуль: — угол между вектором и равен , так как силы, касательные к диску, направлены вдоль радиуса диска в точку касания, следовательно, M = RF.

Поскольку мы имеем дело с телом, который не меняет момент инерции со временем, мы имеем:

Где — момент инерции диска относительно оси, проходящей через его центр.

Подставим числовые значения, получим:

Величина (модуль) касательной силы, приложенной к краю диска, равна 4 N.

🎬 Видео