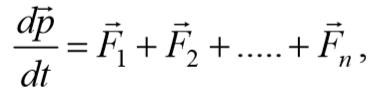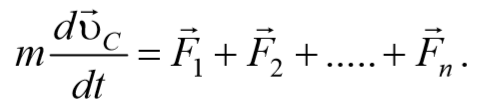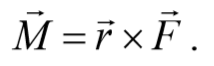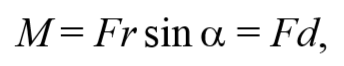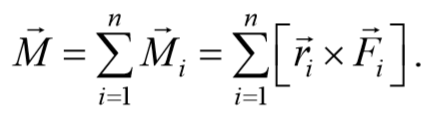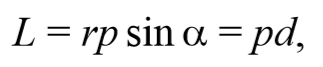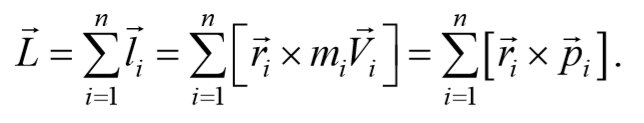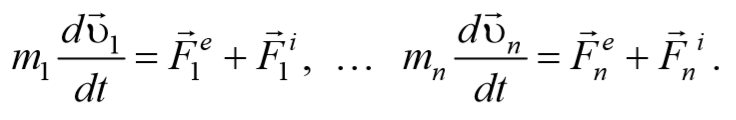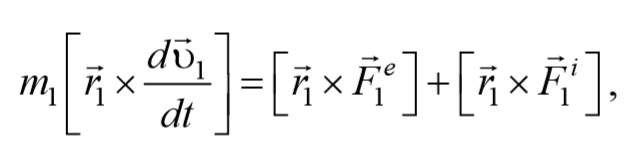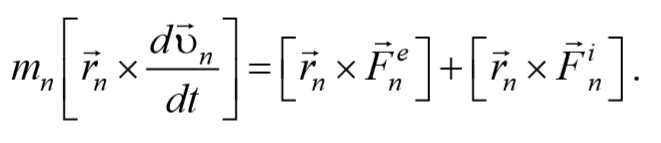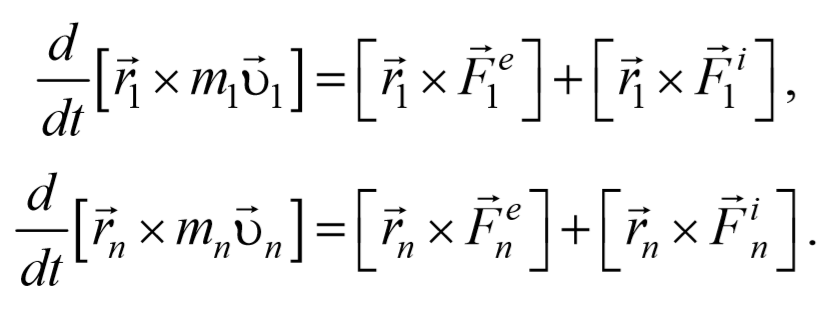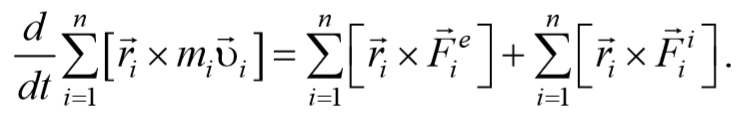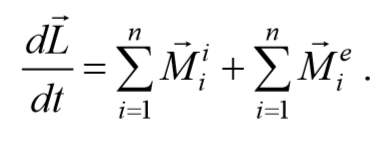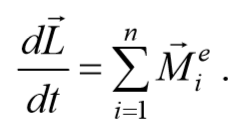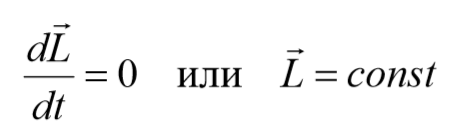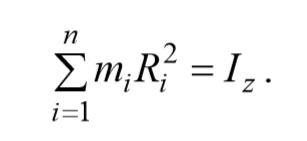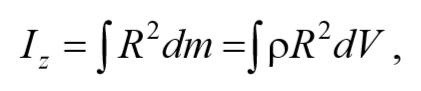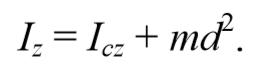Уравнение момента импульса относительно оси

Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства — его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.

Справедливы следующие выражения:

• Момент инерции тела относительно оси вращения — это физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси: [J_ =sum limits _^m_ r_^ ;]
• Момент инерции тела $J_ $ относительно любой оси вращения равен моменту его инерции $J_ $относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями: $J_ =J_ +ma^ $;
• При вращении абсолютно твердого тела вокруг неподвижной оси $z$ его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости: [E_ <k_> =frac <J_omega ^ >;]
• Из сравнения формул $E_ <k_> =frac <J_omega ^ >$и $E_ =frac <mv^>$ следует, что момент инерции — мера инертности тела при вращательном движении;
• Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид: $M_ =J_ varepsilon =frac <dL_>
  $.

Готовые работы на аналогичную тему

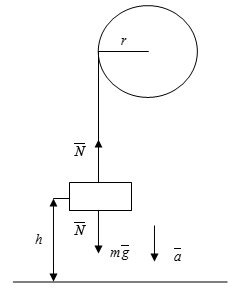
Груз массой 0,8 кг подвешен на тонкой невесомой нити, на высоте 3 м над полом. Нить намотана на сплошной однородный цилиндрический вал радиусом 30 см с моментом инерции 0,15 кг*м2. Вращаясь, вал опускает груз на пол. Определить: время опускания груза до пола, силу натяжения нити, кинетическую энергию груза в момент касания грузом пола.

Запишем закон сохранения энергии для нашей системы:

Записав формулы для пути, линейной и угловой скоростей и подставив в уравнение (1), получим:

Уравнение динамики вращательного движения вала:

Отсюда, сила натяжения нити: $N=frac <J_varepsilon > =frac =4,8H$.

Кинетическая энергия груза в момент удара об пол:

Ответ: $t=3,2A$, $N=4,8H$, $E_ =0,9Дж.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 07 12 2021

Видео:Момент импульсаСкачать

Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА

4.1. Динамика поступательного движения твердого тела.

Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.

Разобьем твердое тело на элементарные массы m_i , тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы

p = $$<sum_^n>$$ m_i υ _i=m υ _C — импульс всех материальных точек твердого тела.

Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс

Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.

4.2. Момент импульса. Момент силы.

Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра

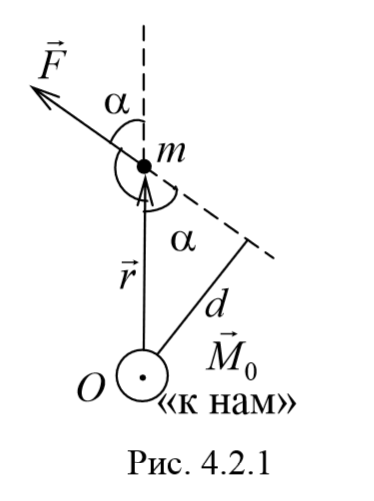
Пусть на частицу массой m действует сила F , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F , и он перпендикулярен как вектору r , так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен

где d=r sin α − плечо силы относительно точки O .

Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.

Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F , действующей на твердое тело, на плечо силы d относительно этой оси.

Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:

Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра

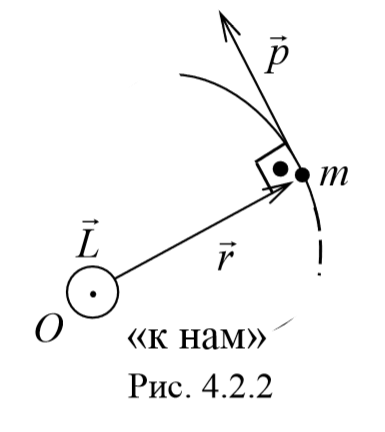
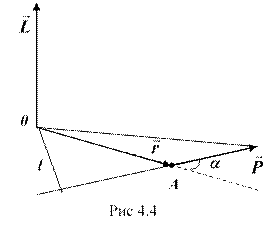
Пусть частица массой m имеет импульс p , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p , и он перпендикулярен как вектору r , так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен

где d − плечо импульса относительно точки O .

Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.

Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.

Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы

4.3. Основное уравнение динамики вращательного движения относительно точки.

Рассмотрим систему материальных точек массами m₁, m₂, . m_n движущихся со скоростями υ ₁, υ ₂, . υ _n . Пусть на каждую из этих точек действуют: равнодействующие внутренних сил F i ₁, F i ₂, . F i _n , и равнодействующие внешних сил F e ₁, F e ₂, . F e _n .

Запишем уравнения движения частиц:

Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим

Преобразуем данные уравнения

Сложим эти уравнения и получим

В последнем уравнении:

Таким образом, выражение (4.3.6) можно записать в виде

Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $$<sum_^n>$$ M i _i=0 , получим основное уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы ).

4.4. Закон сохранения момента импульса.

Если момент внешних сил $$<sum_^n>$$ M e _i=0 , то получим

закон сохранения момента импульса.

Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.

Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.

Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.

4.5. Момент инерции.

Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:

Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м 2 .

Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.

Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:

где R − расстояние от элементарной массы dm до оси вращения.

4.6. Теорема Штейнера. Правило аддитивности

Существуют два свойства момента инерции:

1) Теорема Штейнера: момент инерции тела I_z относительно произвольной оси равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:

2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:

📹 Видео

Уравнение моментов, закон сохранения момента импульса и секториальная скоростьСкачать

Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Момент силы относительно точки и осиСкачать

Сохранение момента импульса при переменном моментеСкачать

Момент инерцииСкачать

Моменты силы, импульса, инерции. Динамика вращательного движенияСкачать

Семинар №5 "Момент силы. Момент импульса" (Чивилев В.И.)Скачать

Момент силыСкачать

Момент импульса. Закон сохранения момента импульса. Физика 10 классСкачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Лекция №5 "Уравнение моментов" (Булыгин В.С.)Скачать

Семинар №6 "Момент инерции. Уравнения моментов" (Чивилев В.И.)Скачать

Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать

Урок 80 (осн). Момент силы. Правило моментовСкачать

5.2. Момент импульса системы материальных точек | Динамика | Александр Чирцов | ЛекториумСкачать

Скамья Жуковского (закон сохранения момента импульса)Скачать