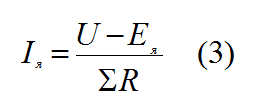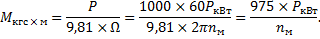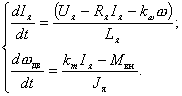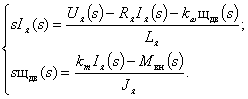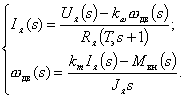В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
- Противо ЭДС двигателя Eя
- Ток якоря Iя
- Частота вращения якоря
- Электромагнитная мощность двигателя
- Электромагнитный момент
- Общие сведения о двигателях постоянного тока
- Энергетическая диаграмма
- Уравнение вращающих моментов
- Уравнение напряжения и тока
- Скорость вращения и механические характеристики
- Основные теоретические положения
- Уравнения, описывающие электрические процессы в ДПТ
- 🌟 Видео
Видео:Схема двигателя постоянного тока. Устройство и принцип работы.Скачать

Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Видео:Электродвигатель постоянного тока. Принцип работы.Скачать

Ток якоря Iя
Выразим из формулы 2 ток якоря.
Видео:Регулирование частоты вращения двигателей постоянного токаСкачать

Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.
Видео:Способы возбуждения электрических машин постоянного токаСкачать

Электромагнитная мощность двигателя
Видео:Принцип работы бесщеточного двигателя постоянного токаСкачать

Электромагнитный момент
где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)
Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
Видео:Пуск двигателей постоянного токаСкачать

Общие сведения о двигателях постоянного тока
Автор: Евгений Живоглядов.
Дата публикации: 01 марта 2013 .
Категория: Статьи.
Двигатели постоянного тока находят широкое применение в промышленных, транспортных и других установках, где требуется широкое и плавное регулирование скорости вращения (прокатные станы, мощные металлорежущие станки, электрическая тяга на транспорте и так далее).
По способу возбуждения двигатели постоянного тока подразделяются аналогично генераторам на двигатели независимого, параллельного, последовательного и смешанного возбуждения.
Схемы двигателей и генераторов с данным видом возбуждения одинаковы (рисунок 1 в статье «Общие сведения о генераторах постоянного тока») . В двигателях независимого возбуждения токи якоря Iа и нагрузки I равны: I = Iа, в двигателях параллельного и смешанного возбуждения I = Iа + iв и в двигателях последовательного возбуждения I = Iа = Iв.
С независимым возбуждением от отдельного источника тока обычно выполняются мощные двигатели с целью более удобного и экономичного регулирования тока возбуждения. По своим свойствам двигатели независимого и параллельного возбуждения почти одинаковы, и поэтому первые ниже отдельно не рассматриваются.
| Рисунок 1. Энергетическая диаграмма двигателя параллельного возбуждения |
Видео:Как увеличить обороты и мощность коллекторного двигателяСкачать

Энергетическая диаграмма
Энергетическая диаграмма двигателя параллельного возбуждения изображена на рисунке 1. Первичная мощность P1 является электрической и потребляется из питающей сети. За счет этой мощности покрываются потери на возбуждения pв и электрические потери pэла = Iа² × Rа в цепи якоря, а оставшаяся часть составляет электромагнитную мощность якоря Pэм = Eа × Iа, которая превращается в механическую мощность Pмх. Потери магнитные pмг, добавочные pд, и механические pмх покрываются за счет механической мощности, а остальная часть этой мощности представляет собой полезную механическую мощность P2 на валу.
Аналогичные энергетические диаграммы, иллюстрирующие преобразование энергии в двигателе, можно построить и для других типов двигателей.
Видео:Способы регулирования частоты вращения якоря машины постоянного токаСкачать

Уравнение вращающих моментов
Электромагнитный момент двигателя
который является движущим и действует в сторону вращения, расходуется на уравновешивание тормозящих моментов: 1) момента M0, соответствующего потерям pмг, pд и pмх, покрываемым за счет механической мощности [смотрите равенство (6) в статье «Общие сведения о генераторах постоянного тока»]; 2) Mв – момента нагрузки на валу, создаваемого рабочей машиной или механизмом; 3) Mдин – динамического момента [смотрите равенство (7) в статье «Общие сведения о генераторах постоянного тока»]. При этом
| Mэм = M0 + Mв + Mдин | (1) |
| Mэм = Mст + Mдин | (2) |
является статическим моментом сопротивления.
При установившемся режиме работы, когда n = const и поэтому Mдин = 0,
| Mэм = Mст. | (3) |
В дальнейшем индекс «эм» у Mэм будем опускать. Обычно M0 мал по сравнению с Mв, и поэтому приблизительно можно считать, что при установившемся режиме работы Mэм = M является полезным моментом на валу и уравновешивается моментом Mв. Можно также значение M0 включить в значение Mв.
Укажем, что если выразить P в киловаттах, а Ω — через число оборотов в минуту nм, то между P, nм и M в кгс × м будет существовать зависимость
Видео:Регулятор скорости двигателя постоянного токаСкачать

Уравнение напряжения и тока
В двигателях направление действия э. д. с. якоря Eа противоположно направлению тока якоря Iа (смотрите статью «Принцип действия машины постоянного тока»), и поэтому Eа называется также противоэлектродвижущей силой якоря. Уравнение напряжения для цепи якоря двигателя можно записать следующим образом:
| U = Eа + Rа × Iа. | (4) |
Здесь Rа – полное сопротивление цепи якоря [смотрите равенство (15) в статье «Общие сведения о генераторах постоянного тока»]. В режиме двигателя всегда U > Eа.
Из равенства (4) следует, что
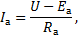 | (5) |
| Eа = cе × Фδ × n. | (6) |
Видео:Характиристики машин постоянного токаСкачать

Скорость вращения и механические характеристики
Решая уравнение (4) совместно с (6) относительно n, находим уравнение скоростной характеристики n = f(Iа) двигателя:
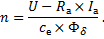 | (7) |
| M = см × Фδ × Iа. | (8) |
Определив отсюда значение Iа и подставив его в (7), получим уравнение механической характеристики n = f(M) двигателя:
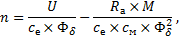 | (9) |
которое определяет зависимость скорости вращения двигателя от развиваемого момента вращения.
Вид механической характеристики n = f(M) или M = f(n) при U = const зависит от того, как с изменением момента M изменяется поток машины Фδ, и различен для двигателей с различными способами возбуждения. Это же справедливо для скоростных характеристик (смотрите статьи «Двигатели параллельного возбуждения», «Двигатели последовательного возбуждения», «Двигатели смешанного возбуждения»).
Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
Видео:Как работает КОЛЛЕКТОРНЫЙ ЭЛЕКТРОДВИГАТЕЛЬ постоянного тока. Самое понятное объяснение! #shortsСкачать

Основные теоретические положения
Важное свойство ДПТ с независимым возбуждением от постоянных магнитов состоит в том, что результирующий момент сил от всех проводников якоря, называемый электромагнитным моментом двигателя M, пропорционален току якоря Iя, потребляемому двигателем от источника питания:
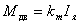
где k m — коэффициент пропорциональности, называемый постоянной момента двигателя. Его размерность [Нм/А]. По законам электромагнитной индукции в проводнике, движущемся в магнитном поле, возникает электродвижущая сила. Суммарная ЭДС катушек якоря E через коллектор и щетки прикладывается к внешним выводам двигателя. В двигательном режиме работы эта ЭДС направлена против внешнего напряжения U я, подведенного к якорю от источника питания. Поэтому ЭДС двигателя часто называется противоЭДС. Она прямо пропорциональна угловой скорости вращения вала двигателя w дв[рад/с]:
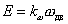
где k ω — коэффициент пропорциональности, называемый постоянной ЭДС двигателя. Его размерность [Вс/рад].
Природа электромагнитных явлений в ДПТ такова, что если используется система единиц СИ, то значения коэффициентов k ω и km численно равны.
Видео:Электродвигатель постоянного токаСкачать

Уравнения, описывающие электрические процессы в ДПТ
В электрической якорной цепи двигателя протекает ток I я под действием напряжения постоянного тока Ua источника питания и противоЭДС двигателя.
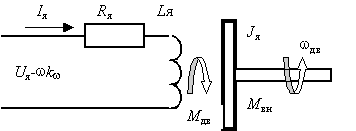
Эта цепь характеризуется параметрами: активным сопротивлением R я [Ом] и индуктивностью L я [Гн] якорной обмотки. Вращающийся ротор, обладающий моментом инерции Ja [Нм с 2 /рад] , приводится в движение одновременным действием электромагнитного момента двигателя M дв и момента внешних сил M вн, приложенного к валу двигателя.
Исходные дифференциальные уравнения ДПТ составляются на основании законов физики. Для электрической цепи используется второй закон Кирхгофа, согласно которому можно записать уравнение
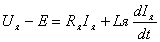
где член R я I я характеризует падение напряжения на активном сопротивлении якорной цепи в соответствии с законом Ома, а член L я ( dI я/ dt ) отражает наличие ЭДС самоиндукции, возникающей в обмотке при изменении тока якоря. В представленном уравнении не учитывается падение напряжения на щетках, зависящее нелинейно от тока якоря, но имеющее, как правило, относительно небольшое значение по сравнению с напряжением U я .
Дифференциальное уравнение, характеризующее процессы в механической части двигателя, составляется на основании второго закона Ньютона:

где M вн — момент внешних сил, действующий относительно оси вращения вала двигателя. В этом уравнении не учитывается действие сил трения, возникающих при вращении ротора, но оказывающих относительно слабое действие на ускорение вала ДПТ.
Используя вышеприведенные формулы и приводя дифференциальные уравнения к нормальной форме Коши, получим описание ДПТ в форме:
Для исследования процессов с помощью ЭВМ удобно использовать структурное представление математической модели ДПТ. Для этого преобразуем полученную систему линейных дифференциальных уравнений по Лапласу при нулевых начальных условиях. В результате получим систему алгебраических уравнений:
в которых s — переменная Лапласа, а величины I я( s ), w дв( s ), U я( s ), M вн( s ) — изображения по Лапласу переменных I я , w дв, U я, M вн соответственно. После эквивалентных преобразований эти уравнения могут быть представлены в форме:
где Тэ = L я / R я — электромагнитная постоянная времени якорной цепи двигателя.
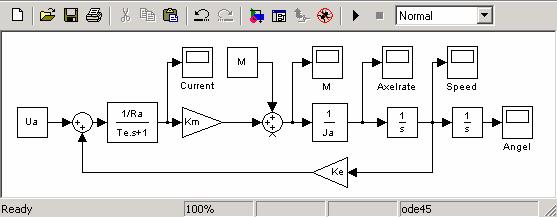
По уравнениям с помощью системы SIMULINK может быть сформирована структурная схема ДПТ для его математического моделирования (рис.1).
Важным параметром ДПТ, определяющим его динамические свойства, является электромеханическая постоянная времени двигателя:
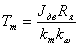
Зависимость между электромагнитным моментом двигателя и частотой вращения ротора в установившемся режиме при постоянных U я и M вн называется механической характеристикой двигателя. Уравнение механической характеристики имеет вид:
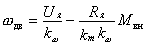
При пуске двигателя, когда скорость равна нулю, развивается пусковой момент

Частота вращения вала двигателя при отсутствии сопротивления называется частотой вращения холостого хода

🌟 Видео
Электрические машины постоянного тока, устройство и принцип действияСкачать

Если подать переменку на двигатель постоянного токаСкачать

Как работают бесколлекторные ЭЛЕКТРОДВИГАТЕЛИ? Вентильный двигатель. Понятное объяснение!Скачать

Проверка двигателя постоянного тока на межвитковое замыкание осциллографомСкачать

Как работает двухфазный ЭЛЕКТРОДВИГАТЕЛЬ? Бесколлекторные VS коллекторные моторы!Скачать

Тормозные режимы двигателей постоянного токаСкачать

Плавный запуск электродвигателя постоянного тока.Скачать

Как определить мощность, частоту вращения, двигателя без бирки или шильдика самому и простоСкачать