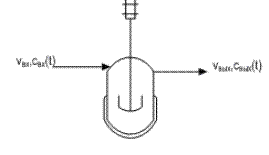
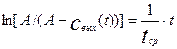На рис.3.1.1 представлена схема аппарата идеального
Рис.3.1.1. Схема аппарата идеального перемешивания.
Аппарат идеального смешения характеризуется тем, что интенсивность перемешивания в нем настолько велика, что поступающее с потоком вещество мгновенно распространяется по всему объему аппарата и появляется в выходном потоке. Таким образом, в таком аппарате любое возмущение на входе мгновенно появляется на выходе. Составим для такого аппарата уравнение материального баланса при следующих условиях:
1. Объемный расход жидкости постоянный.
2. Объем жидкости в аппарате постоянный.
3. Концентрация индикаторного вещества (трассера) на выходе из аппарата, равна концентрации его в аппарате (условия идеального смешения).
4. В аппарате соблюдаются условия квазистационарности – изменение концентрации во входном потоке происходит медленнее, чем устанавливается равномерное распределение вещества по всему объему.
Составим уравнение материального баланса вещества для этого аппарата.
Входной поток вещества будет равен
Выходной поток вещества будет равен:
Накопление вещества в аппарате за время от 0 до t, будет равно
(3.1.3)
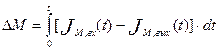
Продифференцируем уравнение (3.1.3) по времени с учетом того, что масса вещества в аппарате будет равна произведению концентрации на объем аппарата, и используем для потоков выражения (3.1.1) и (3.1.2):
(3.1.4)
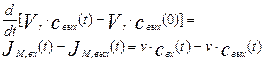
Где Vr – объем аппарата в м 3 .
Учитывая, что в начальный момент времени концентрации в аппарате была постоянной величиной, разделим обе части уравнения (3.1.4) на объемный расход смеси v и перенесем второе слагаемое правой части в левую часть. В итоге получим следующее уравнение:
(3.1.5)
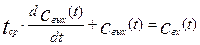
Где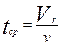 
— среднее время пребывания смеси в аппарате, [c.], t-текущее время, [c].
Полученное дифференциальное уравнение (3.1.5) представляет собой математическую модель аппарата идеального перемешивания. Для того чтобы узнать, как изменяется свых(t), необходимо решить уравнение (3.1.5) при заданной функции свх(t) (внешнее воздействие).
В качестве типовых внешних воздействий при анализе поведения объектов чаще всего используют следующие виды воздействий:
· Ступенчатое воздействие свх(t)= А=const
· Импульсное воздействие свх(t)=d(t)-функция Дирака.
· Синусоидальное воздействие свх(t)=C0 sin(wt)
Рассмотрим решение уравнения (3.1.5) при ступенчатом входном воздействии. Тогда уравнение (3.1.5) принимает вид:
(3.1.6)
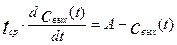
Уравнение (3.1.6) можно решить разделением переменных. Для этого разделим обе части уравнения (3.1.6) на величину времени контакта tср и произведем операцию разделения переменных. В результате получим уравнение в полных дифференциалах:
(3.1.7)
После интегрирования уравнения (3.1.7) получаем:
(3.1.8)
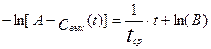
Где В – постоянная интегрирования, которая может быть определена из начальных условий: при t=0 cвых(t) = 0. Отсюда получаем, что -ln(A)=ln(B).
Подставляя найденное значение произвольной постоянной в уравнение (4.1.8), получим:
(3.1.9)
После потенцирования окончательно получим
(3.1.10)
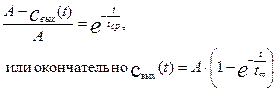
На рис.3.1.2 представлен график изменения выходной концентрации при воздействии на вход единичного ступенчатого возмущения. Если в уравнении (3.1.10) принять t=tср, тогда получим:
(3.1.11)
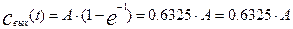
Полученное значение свидетельствует о том, что среднее время пребывания в аппарате идеального перемешивания есть время, в течение которого выходной параметр свых(t) изменится на 63.25% от величины нанесенного на объект возмущения..
 |
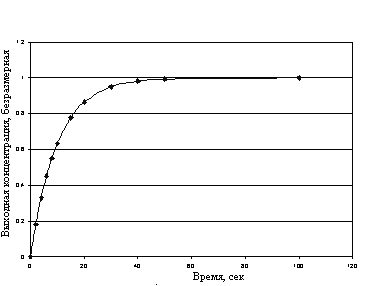Рис.3.1.2 . Кривая разгона аппарата идеального перемешивания на ступенчатое единичное возмущение входа.
Среднее время пребывания tср является параметром модели аппарата идеального перемешивания, Модель аппарат идеального перемешивания применяется для аппаратов, у которых обеспечиваются условия интенсивного перемешивания, и время смешения много меньше среднего времени пребывания вещества в аппарате. Cреднее время пребывания может быть определено из экспериментально полученной кривой разгона следующим образом: Если прологарифмировать уравнение (3.10), мы получим уравнение
Это уравнение представляет собой уравнение прямой в координатах
. При этом тангенс угла наклона этой прямой есть величина, обратная времени пребывания. На следующем рисунке представлена графическая зависимость для определения среднего времени пребывания по экспериментальной кривой разгона.
 |
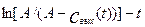
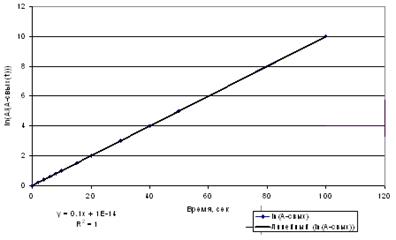Рис.3.1.3. Определение времени пребывания по кривой разгона.
Видео:Химические реакторыСкачать
Уравнение модели идеального перемешивания для температуры
Для поверочного расчета имеем
[ Второй корень уравнения (18) отрицателен и потому лишен физического смысла].
Для проектного расчета можно записать
О реалистичности моделей идеальных потоков .
Идеальные потоки – сильно упрощенные модели. Законен вопрос: насколько можно считать их соответствующими каким-либо реальным объектам. Оказывается, такое соответствие существует достаточно часто .
Так, к идеальному вытеснению близок поток жидкости или газа через достаточно длинный аппарат, заполненный слоем зернистого материала (насадочная колонна, реактор с неподвижным слоем катализатора, шахтная печь). Зернистый слой интенсивно выравнивает поток. В меньшей степени можно применить эту модель к потоку в пустой трубе, особенно в ламинарном режиме .
Близко к идеальному смешению течение жидкости через аппарат с мешалкой, через барботажный слой. В том же барботажном слое течение газа плохо описывается данной моделью, но часто нам нужно описать именно движение жидкости .
В практических расчетах процессов мы во многих случаях удовольствуемся моделями идеальных потоков. Так, рассчитывая время контакта (время протекания реакции) в каталитическом реакторе или скорость газа в насадочной колонне, мы не принимаем во внимание реальную неравномерность, размытость этих величин, т. е. ведем расчет в приближении идеального вытеснения. С другой стороны, рассчитывая выпарной аппарат с принудительной циркуляцией, мы, как правило, считаем концентрацию упариваемого раствора одной и той же во всем объеме, что соответствует идеальному смешению .
Часто такое пренебрежение неидеальностью потока действительно допустимо, и тогда, разумеется, применять более сложные модели нецелесообразно. Но есть и случаи, когда недопустимо грубо пользоваться приближением идеальных потоков. Поэтому очень важно в каждом конкретном случае оценить возможную ошибку идеализации, обусловливающую неадекватность модели .
Сопоставление идеальных потоков проведем таким образом, как будто имеем дело с реальными аппаратами (можно иметь в виду случаи, когда данное описание достаточно точно). Вначале сопоставим особенности описания, а затем – протекание в этих потоках различных процессов .
Каждый из идеальных потоков отличает предельная равномерность. В идеальном вытеснении это равномерность скоростей и времени пребывания, в идеальном смешении – равномерность концентраций и температуры по объему .
Стационарный процесс в потоке идеального вытеснения описывается системой дифференциальных уравнений типа (1). Для идеального смешения этот случай описывается уравнениями (9) или (11) – конечными уравнениями, не содержащими оператора дифференцирования. Лишь в нестационарном случае в описании появляются производные – см. уравнения (10), (12). Объясняется это тем, что в идеальном смешении равны нулю производные по координатам – градиенты концентраций и температуры .
В связи с этим процесс в данном потоке можно описывать так, будто он целиком происходит в одной точке (от точки к точке ничто не меняется). И в нестационарном процессе аппарат идеального смешения ведет себя «как точка» – все изменения происходят во всем объеме одновременно. Такой объект называют объектом с сосредоточенными параметрами. Аппарат идеального вытеснения – объект с распределенными параметрами: в нем параметры процесса меняются от точки к точке. Правда, это простейший из таких объектов – одномерный, поскольку рассматриваются изменения лишь в продольном направлении, а поперек потока все считается выровненным. Тем не менее, описание идеального смешения еще проще. Эта простота привлекательна с точки зрения математической обработки модели; поэтому, как увидим ниже, ряд более сложных моделей строится на основе модели смешения .
Посмотрим теперь, как равномерность или неравномерность распределения параметров влияет на ход химической реакции. Рассмотрение будем проводить на примере простейшей реакции :
Рис . 5 . График изменения концентрации реагента по длине
аппарата: 1 – поток идеального вытеснения; 2 – поток идеального смешения .
Многие выводы из нашего рассмотрения будут верны для большинства формально простых реакций, обратимых реакций, а также для процессов массо- и теплообмена, формальное описание которых аналогично описанию обратимой реакции 1-го порядка .
Вначале проведем качественный анализ. Равномерность времени пребывания в идеальном вытеснении способствует глубокому протеканию реакции, так что преимущество следует отдать потоку вытеснения .
Как влияет на процесс равномерность концентраций в потоке смешения ? Построим график изменения концентрации реагента А по длине l аппарата идеального вытеснения , либо идеального смешения ( рис. 5 ). На графике l =0 – вход в аппарат ; l = L – выход. Значения l l > L соответствуют трубам, подводящим жидкость к аппарату и отводящим прореагировавшую смесь. Будем считать заданными исходную концентрацию с ао и конечную с Ак .
В идеальном вытеснении легко связать пройденный частицей путь с временем протекания реакции в этой частице
где w — линейная скорость .
Уравнение ( 2 ) соответственно получит вид
( см. экспоненту на рисунке ).
В аппарате смешения картина совершенно иная. На входе происходит скачок концентрации А до значения, которое дальше сохраняется вплоть до выхода. По всей длине аппарата с а = с а к .
Если теперь рассмотреть одно и то же произвольное поперечное сечение обоих аппаратов, то, очевидно, значение с а в аппарате вытеснения окажется больше соответствующего значения в аппарате смешения. Скорость реакции, пропорциональная с а , во всех сечениях аппарата, кроме последнего (на выходе), также будет большей в аппарате вытеснения, чем в аппарате смешения. Получить картину, показанную на рис. 5 (одинаковые начальные и одинаковые конечные с а ), можно только, если объем аппарата смешения больше объема аппарата вытеснения .
Отсюда можно сделать два вывода: 1) аппарат вытеснения обеспечивает большую эффективность процесса; 2) на кинетику реакции влияет не только химизм, но и характер потока .
Таким образом, и анализ распределения времени пребывания, и анализ распределения концентрации приводят к выводу о большей эффективности потока вытеснения. Правда, судить об эффективности только по скорости протекания реакции нельзя. Конструкции аппаратов, близких к идеальному вытеснению и к идеальному смешению, различны. В частности, интенсивное перемешивание способствует массо- и теплообмену. Часто процессы, для которых важен перенос тепла и вещества, проще оформить в аппарате с перемешиванием, и тогда возникает проблема: чем жертвовать – простотой конструктивного оформления или отсутствием продольного перемешивания .
Пример 3 . Проблема выбора типа аппарата .
Проектируется аппаратурное оформление сильно экзотермической каталитической реакции. Можно поместить неподвижный катализатор в трубки – поток будет близок к идеальному вытеснению. Но для обеспечения отвода тепла трубки придется делать узкими, и следовательно, при данном обгеме катализатора их будет много. Промышленные реакторы этого типа содержат по нескольку тысяч трубок – это сложные и дорогие аппараты .
Можно применить псевдоожиженный слой катализатора – отвод тепла упростится, хотя вследствие влияния продольного перемешивания придется брать больший объем аппарата и большее количество катализатора .
Решение вопроса об эффективности того или иного потока должно, разумеется, базироваться на количественных оценках, к которым мы и перейдем. По-прежнему будем анализировать реакцию (21) .
Можно сопоставить выражения (3) и (16) . Задав ряд значений , рассчитаем при каждом из них степень превращения в потоках идеального вытеснения х выт и идеального смешения х см :
При малых значениях , соответствующих случаям малого объема аппарата или медленной реакции , разница не очень велика (
6% при = 0,5 ). При росте разница может оказаться очень большой .
Еще яснее видно различие при сопоставлении результатов проектного расчета, когда задается требуемая величина х и по формулам (4) и (17) совместно с (1) рассчитываются потребные объемы аппаратов . Приведем значения отношения этих объемов V см / V выт при различных требуемых х :
Результаты последнего сопоставления очень показательны. Если требуется невысокая степень превращения (менее 0,9), то проигрыш вследствие перехода от идеального вытеснения к идеальному смешению не слишком велик. Оценивая эффективность, нужно учитывать и иные факторы. Но если требуется степень превращения 99% или выше, различие столь велико (в десятки или даже сотни раз), что ясно: необходимо применять аппараты, максимально близкие к идеальному вытеснению :
Пример 4 . Проблема выбора типа аппарата .
Продолжим рассмотрение, начатое в примере 3. То обстоятельство, что при небольших степенях превращения проигрыш вследствие продольного смешения невелик, позволяет решить две задачи (отвод тепла и глубокое превращение реагентов) порознь, в разных аппаратах .
Вначале можно поставить аппарат с интенсивным перемешиванием, получая в нем степень превращения 80–90% и соответственно отводя 80–90% всего выделяющегося тепла. А затем направить реагирующую массу в аппарат вытеснения, где превращение доходит до высокой степени. В этом аппарате отвод тепла упрощен, так как основная часть его уже отведена на предыдущей ступени .
Вывод о том, что в аппарате вытеснения глубина превращения выше, чем в аппарате смешения, и что преимущество этого потока возрастает по мере роста требуемой степени превращения, верен для изотермических необратимых и обратимых реакций любого порядка (кроме нулевого), а также для большинства тепло- и массообменных процессов. Можно показать, что по глубине протекания процесса поток идеального вытеснения теоретически наилучший для всех процессов, скорость которых падает по мере протекания процесса .
Иногда делают обратный вывод, считая, что если один идеальный поток – Наилучший, то второй (смешение ) – наихудший. Но это неверно. Существуют потоки, много худшие, чем идеальное смешение – прежде всего это потоки c большими застойными зонами или мощными короткими байпасами .
Нужно также иметь в виду, что существует ряд процессов, в которых закон изменения скорости по ходу процесса иной. Вначале скорость мала, постепенно она нарастает и затем, достигнув максимума, начинает спадать (рис. 6). Объясняется это тем, что в процессе вырабатывается какая-либо субстанция (вещество или энергия), ускоряющая процесс. Вначале этой субстанции мало, процесс медленный. По мере протекания он самоускоряется до максимума, после которого скорость падает вследствие нехватки исходного вещества. Отметим 4 группы таких процессов .
Автокаталитические реакции , в которых один из продуктов реакции ускоряет процесс. Пока этого продукта мало, реакция медленная. Накопление катализатора ведет к ускорению реакции до тех пор, пока в конце процесса убыль исходных веществ не обусловит снижение скорости .
Биохимические реакции , вызываемые микроорганизмами – брожение, ферментация. На начальной стадии процесса его скорость возрастает в связи с интенсивным размножением микроорганизмов. В конце процесс замедляется вследствие недостатка пищи .
Экзотермические реакции , в которых вначале за счет тепла реакции происходит разогрев, ведущий к росту скорости .
Процессы кристаллизации . В начальной стадии процесса скорость растет благодаря увеличению числа зародышей кристаллизации. Затем образование новых зародышей прекращается, и скорость снижается вследствие уменьшения пересыщения .
Если процесс такого типа проводить в аппарате вытеснения, то на начальном отрезке аппарата скорость мала, и эта его часть используется неэффективно. В таком случае более эффективным может оказаться аппарат смешения: в нем просто поддерживать высокую концентрацию катализатора, микроорганизмов, зародышей кристаллизации или высокую температуру. Причем эта оптимальная концентрация или температура поддерживается во всем объеме аппарата .
После того, как процесс пройдет через максимум скорости, он будет идти как процесс с падающей скоростью. Поэтому на этом этапе (на «хвосте» процесса) смесь выгодно вывести из аппарата смешения и направить в аппарат вытеснения .
В ряде подобных случаев процесс можно проводить и в аппарате вытеснения, но тогда для ускорения процесса на начальной стадии осуществляют циркуляцию: часть потока, выходящего из аппарата, возвращают на его вход (рис. 7). С этим циркуляционным потоком в начальный участок аппарата вносится «затравка», ускоряющая процесс. Можно отметить, что циркуляция вообще влияет аналогично продольному смешению .
Сложные реакции в идеальных аппаратах .
При проведении сложных реакций с побочными стадиями обычно главной задачей является достижение высокой селективности. Зачастую ради этого жертвуют степенью превращения: недопревратившиеся реагенты можно отделить от вышедшей из аппарата смеси и вернуть в начало процесса. В результате стоимость переработки возрастает на величину стоимости процесса разделения. Низкая же селективность означает, что, во-первых, часть исходных веществ затрачивается бесполезно (переходит в ненужные побочные продукты). Во-вторых, эти побочные продукты также приходится отделять :
затраты на разделение могут быть даже большими, чем при низкой степени превращения. И в-третьих, с побочными продуктами после их отделения нужно что-то делать. Просто выбросить их, как правило, нельзя: загрязнение окружающей среды в наше время становится одной из тяжелейших проблем, стоящих перед человечеством. Обезвреживание или уничтожение побочных продуктов ложится тяжелым грузом на экономику процесса .
Рис. 6. График изменения во времени скорости процесса с самоускорением .
Рис. 7. Схема аппарата с циркуляцией .
Характер влияния потока на сложные реакции отличается большим разнообразием. Рассмотрим два простых случая: реакцию с последовательной побочной стадией и реакцию с параллельной побочной стадией .
Рис.8. График изменения концентраций во времени для последовательной реакции: 1 – исходное вещество А; 2 – целевой продукт В ;
3 – побочный продукт С .
На рис. 8 показано изменение концентрации по времени протекания последовательной реакции :
Если В – целевой продукт, а С – отброс, то концентрация целевого продукта вначале растет, проходит максимум и далее падает. Можно показать, что селективность этой реакции падает с самого начала . Оптимальными будут условия, когда ев не дошло до максимума: хотя при этом степень превращения А мала, но зато велика селективность. Если реакция проходит в аппарате идеального вытеснения, то состав смеси будет соответствовать определенному значению t (см. рис. 8) .
В потоке смешения положение будет иным. Наряду с частицами, выходящими из аппарата через малое время после входа, найдутся и такие, которые задерживаются в нем намного дольше среднего. Как видно из рис. 8, в этих частицах практически весь реагент А превратится в побочный продукт С. Этот отброс будет загрязнять выходящую смесь, снижая селективность .
Пример 5 . Расчет селективности последовательной реакции. Примем в реакции (23) условие k 1 = k 2 = k . Тогда для идеального вытеснения система уравнений кинетики будет иметь вид (для концентрации С приведено уравнение стехиометрического баланса):
откуда для степени превращения А и селективности легко получить уравнения
Для идеального смешения уравнения материального баланса по А и по В будут иметь следующий вид (для С верно записанное выше стехиометрическое соотношение ):
Легко получить решение этих уравнений
Сопоставление формул (24) – (27) показывает, что при равных значениях х величина о в аппарате идеального вытеснения окажется заметно выше, чем в аппарате идеального смешения (рис. 9 ).
Рис . 9 . Зависимость селективности от степени превращения
реагента : 1 – идеальное вытеснение ; 2 – идеальное смешение .
Если бы целевым продуктом было вещество С , то выход его был (при заданном ) много больше в потоке вытеснения, чем в потоке смешения. И в этом случае поток вытеснения был бы предпочтительнее.
Для параллельной реакции (В – целевой продукт )
влияние структуры потока на селективность зависит от соотношения порядков основной и побочной стадии .
Если обе стадии – одинакового порядка , то соотношение скоростей образования обоих продуктов зависит только от соотношения констант скорости
В этом случае селективность не меняется по ходу реакции (если не меняется температура) и не зависит от типа потока .
Теперь пусть первая стадия — первого порядка, а вторая – второго . Рассчитаем отношение r B к r C
Это отношение , а стало быть , и селективность тем больше , чем меньше c A .
Обратимся к рис. 5. При заданной степени превращения А его концентрация в любом поперечном сечении аппарата смешения будет ниже, чем в соответствующем сечении аппарата вытеснения. Значит, в этом случае процесс в аппарате идеального смешения будет проходить хотя и медленнее, но зато с существенно большей селективностью, т. е. именно аппарат смешения окажется наилучшим .
Нетрудно понять, что если целевая реакция – второго порядка, а побочная – первого, то все преимущества будут на стороне идеального вытеснения .
Рассмотрим процессы полимеризации в потоке. Реакция полимеризации состоит из чрезвычайно большого числа последовательных стадий присоединения молекул мономера к растущей цепи. В этом случае нельзя говорить о целевом веществе: продукт представляет собой смесь макромолекул разной длины. Эту смесь можно охарактеризовать функцией распределения степени полимеризации (или длины цепей). Свойства полимера существенно зависят как от средней длины цепей (математического ожидания), так и от дисперсии этой величины. В большинстве случаев стремятся получить молекулярно однородный полимер: продукт с малой дисперсией степени полимеризации .
Теоретические исследования и математическое моделирование показали, что влияние структуры потока на распределение степени полимеризации зависит от особенностей кинетики полимеризации. Можно выделить два крайних случая .
Рис . 10 . График интегральных функций распределения степени
полимеризации N полистирола .
Медленный рост цепей , который продолжается на протяжении всего времени пребывания и прерывается на выходе из аппарата. Тогда длина цепи в основном определяется временем пребывания»
и наибольшая однородность цепей будет достигаться в аппарате вытеснения .
Быстрый рост цепей , при котором время роста отдельной цепи мало. За время пребывания в аппарате многократно наступают начало и конец роста цепи. Длина цепи в основном определяется концентрациями мономера и других веществ (инициатора полимеризации, регулятора длины и пр.) в период ее роста. Поэтому молекулярной однородности будет способствовать идеальное смешение, выравнивающее концентрации по всему аппарату. В аппарате вытеснения в этом случае цепи, выросшие в начале аппарата (высокая концентрация мономера), будут сильно отличаться от тех, что выросли в его конце .
Пример 6 . Влияние турбулентности на полимеризацию. Исследована реакция анионной полимеризации стирола с целью получения максимальной молекулярной однородности. Примерно за 1 мс стирол смешивали с инициатором и пропускали по трубке (полимеризатору). Среднее время пребывания составляло от 0,1 до 2 с; после выхода из трубки полимеризация прекращалась.
На рис . 10 показаны интегральные функции распределения степени полимеризации N , полученные при разных значениях критерия Рейнольдса . Переход от ламинарного потока ( Re = 1000 ) к развитому турбулентному ( Re = 15000 ) привел к резкому снижению дисперсии N .
Видео:Основные модели гидродинамики – идеальное вытеснение, идеальное смешение, диффузионная и ячеечнаяСкачать
Модель идеального смешения
Модель идеального смешения относится к классу моделей с сосредоточенными параметрами. Для таких моделей характерно постоянство перемешивания в пространстве. Математическое описание включает алгебраические уравнения или дифференциальные уравнения I-го порядка для нестационарных процессов.
Модель идеального смешения соответствует аппарат, в котором поступающее в него вещество мгновенно распределяется по всему объему аппарата. Концентрация вещества в любой точке аппарата равна концентрации на входе из него.
Зависимость концентрации вещества в потоке жидкости на входе в аппарате идеального смешения cвх и выходе их него cвых (рис.1) имеет вид: 
, (1)
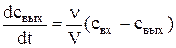
где cвх — концентрация вещества на входе; свых — концентрация вещества на выходе; V — объем аппарата, м 3 ; n — объемный расход потока через аппарат,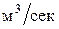 
. Для решения дифференциального уравнения (1) начальным условием является: в начальный (нулевой) момент времени в аппарате начальная концентрация была равна некоторому начальному значению cн, т.е. с(0) = сн.
В лабораторных условиях, для исследования изменения концентрации в потоке на выходе из аппарата, используют два различных приема: когда на входе аппарата импульсное возмущение и применяется метод вымывания и когда на входе ступенчатое введение индикатора со скачкообразным изменением концентрации.
При импульсном введении индикатора в количестве g, он мгновенно распределяется по всему объему аппарата и затем начинается его вымывание. Изменение концентрации на выходе потока из аппарата описывается уравнением
, (2)
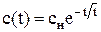
где сн — начальная концентрация,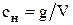 
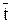
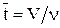
; t — исследуемый интервал времени; 
— среднее время пребывания частиц потока в аппарате, 
.
Если на вход аппарата подано ступенчатое воздействие, т.е. скачкообразное изменение концентрации в момент времени t = 0 от c = 0 до c = cвх , то уравнение изменение концентрации на выходе потока из аппарата примет вид
. (3)
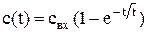
Аппарат идеального смешения может быть аппроксимирован апериодическим звеном первого порядка с передаточной функцией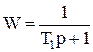 
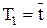
, где Т1 -постоянная времени объекта, 
.
Моделью идеального смешения описываются процессы, происходящие в цилиндрических аппаратах со сферическим дном в условиях больших скоростей перемешивания и при наличии отражающих перегородок.
🎬 Видео
Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать
Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать
Модели реакторов идеального вытеснения и идеального смешенияСкачать
Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать
Урок 166. Предмет термодинамики. Внутренняя энергия телаСкачать
Моделирование химико-технологических процессов. Часть 1. Уровень: базовый.Скачать
Урок 139. Основные положения МКТ.Скачать
Проверим уравнение состояния идеального газаСкачать
Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать
Молекулярно-кинетическая теория. МКТ за 30 минут | ЕГЭ Физика | Николай НьютонСкачать
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать
Мультифизическое моделирование химических реакторов в COMSOL Multiphysics®. Версия 6.0Скачать
Лекция №1 "Основные понятия молекулярной физики"Скачать
Тема 2. Макро и микропараметры. Идеальный газ. Основное уравнение МКТ идеального газаСкачать
Физика 10 класс (Урок№23 - Внутренняя энергия. Работа. Количество теплоты.)Скачать
Внутренняя энергия. Способы изменения внутренней энергии. 8 класс.Скачать
Основные положения молекулярно-кинетической теории | Физика 10 класс #24 | ИнфоурокСкачать
Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать
