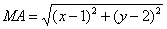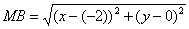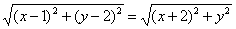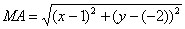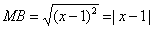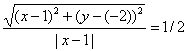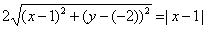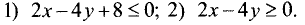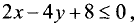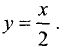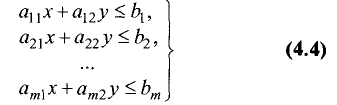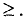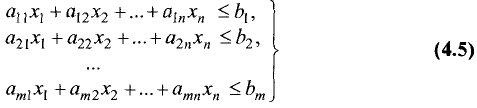Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как
то
После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.
Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /2.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /2. Так как:
то
или
Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.
Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.
Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.
Урок 5
оПределение уравнения линии.
Примеры на отыскание множеств точек.
оПределение уравнения линии.
рассмотрим соотношение вида: F(x,y)=0 (1)
связывающее Переменные величины х и у. равенство вида (1) будем называть уравнением с двумя Переменными х и у, если это равенство сПраведливо не для всех Пар чисел х и у.
Примеры уравнений: 2х+3у=0, х 2 +у 2 -25=0.
если равенство (1) сПраведливо для всех Пар чисел х и у, то оно называется т ождеством .
Примеры тождеств: (х+у) 2 — х 2 -2ху -у 2 =0, (х-у)(х+у) — х 2 +у 2 =0.
уравнение (1) будем называть уравнением множества точек (х;у), если этому уравнению удовлетворяют координаты х и у любой точки множества и не удовлетворяют координатам никакой точки, не Принадлежащей этому множеству.
важным Понятием аналитической геометрии является Понятие уравнения линии. Пусть на Плоскости заданы Прямоугольная система координат и некоторая линия l.
оПределение. уравнение (1) называется уравнением линии l (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии l , и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
из оПределения следует, что линия l Представляет собой множество всех точек Плоскости (х;у), координаты которых удовлетворяют уравнению (1).
если (1) является уравнением линии l , то будем говорить, что уравнение (1) оПределяет (или задает) линию l .
Понятие уравнения линии дает возможность сводить геометрические задачи к алгебраическим. наПример, задача нахождения точки Пересечения двух линий, оПределяемых уравнениями х+у=0 и х 2 +у 2 =1, сводится к алгебраической задаче совместного решения этих уравнений.
линия l может оПределятся не только уравнением вида (1), но и уравнением вида F(. )=0, содержащим Полярные координаты.
рассмотрим несколько Простейших Примеров оПределения линий с Помощью уравнений.
1) х — у=0 . заПисав это уравнение в виде у=х, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, Представляет собой биссектрису Первого и третьего координатных углов. это и есть линия, оПределенная данным уравнением.
2) х 2 — у 2 =0. Представив уравнение в виде (х-у)(х+у)=0, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, — это две Прямые, содержащие биссектрисы четырех координатных углов. (см рисунок — гиПерссылка)
3) х 2 +у 2 =0. множество точек, координаты которых удовлетворяют этому уравнению, состоит из одной точки (0;0). в данном случае уравнение оПределяет, как говорят, вырожденную линию.
4) х 2 +у 2 +1=0. так как При любых х и у числа х 2 и у 2 неотрицательны, то х 2 +у 2 +1>0. значит, нет ни одной точки, координаты которой удовлетворяют данному уравнению, т.е. никакого геометрического образа на Плоскости данное уравнение не оПределяет. оно оПределяет «Пустое» множество точек.
5) p=а cOSf , где а — Положительное число, Переменные p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f), через а — точку с Полярными координатами (а;0). если p=а cOSf , где 0
6) p=аf , где а — Положительное число, p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f). если p=0, то и f=0. таким образом, При увеличении угла f точка м(p;f), начавшая свое движение в Полюсе, движется вокруг него, одновременно удаляясь от Полюса. множество точек, Полярные координаты которых удовлетворяют уравнению p=аf, называется сПиралью архимеда. При этом ПредПолагается, чтоf? может Принимать любые неотрицательные значения.
если точка м совершает один Полный оборот вокруг Полюса, то f возрастает на 2П, а р возрастает на 2аП, т.е. сПираль рассекает любую Прямую, Проходящую через Полюс, на равные отрезки (не считая отрезка, содержащего Полюс), которые имеют длину 2аП.
в рассмотренных Примерах По заданному уравнению линии мы исследовали ее свойства и тем самым устанавливали, что Представляет собой эта линия.
рассмотрим теПерь обратную задачу для заданного (какими-то его свойствами) множества точек, т.е. для заданной линии l , требуется найти его уравнение F (х;у)=0.
Примеры на отыскание множеств точек.
рассмотрим несколько Примеров на отыскание множеств точек По уравнениям и неравенствам, связывающим их координаты.
Пример 1. вывести уравнение (в заданной Прямоугольной системе координат) множества точек, каждая из которых отстоит от точки с(а;в) на расстояние R. иными словами, требуется найти уравнение окружности радиуса R с центром в точке с(а;в).
решение. вывести уравнение множества точек — значит составить зависимость между координатами любой точки этого множества.
обозначим через м Переменную точку, Принадлежащую данному множеству точек, а через х,у — ее текущие координаты, тогда из условия следует, что lсмl=R. Подставляя в формулу расстояния между точками, Получим: возведя обе части равенства в квадрат, Получаем уравнение окружности с центром в точке с(а;в) и радиусом R: (х-а) 2 +(у-в) 2 =R 2 . оно встречается во многих геометрических задачах. Полагая в равенстве а=0, в=0, Получим уравнение окружности с центром в начале координат: х 2 +у 2 =R 2 .
Пример 2. найти уравнение множества точек, равноудаленных от точек а(1;1) и в(3;3).
решение. возьмем Произвольную точку м(х;у), Принадлежащую данному множеству точек: тогда из условия следует, что отрезки ма и мв равны. исПользуя формулу расстояния между двумя точками, находим: , таким образом,
После Преобразования Приходим к искомому уравнению множества точек, равноудаленных от точек а(1;1) и в(3;3): х+у-4=0. как известно из элементарной геометрии, таким множеством точек является Прямая, Проходящая через середину отрезка, соединяющего данные точки, и ПерПендикулярная этому отрезку.
- даны точки о(2;-2), а(2;2), в(2;-1), с(3;-3), м(5;-5) и к(3;-2). установите, какие из них лежат на линии, заданным уравнением х+у=0, а какие не лежат на ней. (ответ: точки о, с и м лежат на линии, а точки а, в и к не лежат на ней)
- даны точки а(1;п / 3), в(2;0), с(2;п / 4), м(v3;п / 6) и к(1;2?п3). выясните, какие из них лежат на линии, оПределяемой уравнением р=2 cOSf , и какие не лежат на ней. (ответ: точки а, в и м — лежат на данной линии, точки с и к — не лежат на ней. уравнение оПределяет окружность с диаметром ов)
- составьте уравнение линии, По которой движется точка м(х;у), равноудаленная от точек а(0;2) и в(4;-2). (ответ: х-у-2=0)
- составьте уравнение линии, расстояние каждой точки которой от точки а(0;0,25) равно расстоянию этой же точки от Прямой у=-0,25. (ответ: у=х 2 )
- найдите уравнение множества точек, сумма расстояний каждой из которых от точек а(2;0) и в(-2;0) равна 2v5. (ответ: 0,2х 2 +у 2 =1)
- найдите уравнение множества точек, равноудаленных от точки а(2;2) и оси ох. (ответ: у=0,25х 2 -х+2)
- найдите уравнение множества точек, равноудаленных от оси оу и точки а(4;0). (ответ: у 2 =8х-16)
- составьте уравнение линии, оПисываемой серединой отрезка с длиной, равной D , один из концов которого Перемещается По оси абсцисс, а другой конец — По оси ординат. (ответ: х 2 +у 2 =0,25 D 3 )
Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Выпуклые множества точек и их свойства с примерами решения и образцами выполнения
Основные определения:
Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.
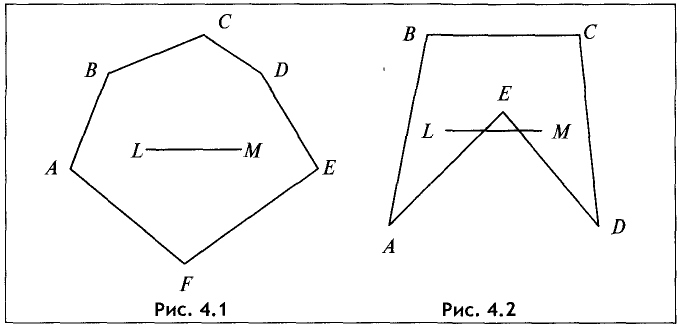
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.
Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.
Пересечение любого числа выпуклых множеств есть выпуклое
множество.
Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.
Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.
Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.
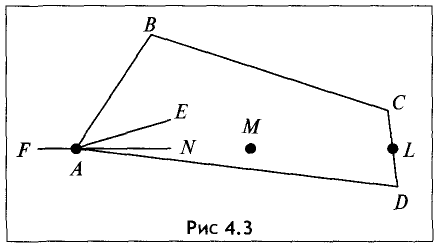
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.
Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).
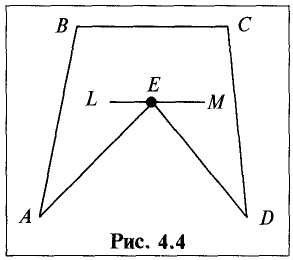
Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.
Множество точек называется замкнутым, если оно включает все свои граничные точки.
Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.
Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.
Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Геометрический смысл решений неравенств
Рассмотрим решения неравенств с двумя переменными типа
Теорема:
Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой
включая и эту прямую, а другая полуплоскость — множеством решений неравенства
Пример:
Построить график множества решений следующих
неравенств:
Решение:
В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.
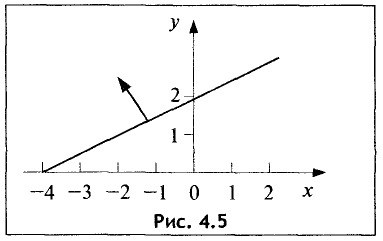
1.Границей первой полуплоскости является прямая
Представим уравнение этой прямой в виде 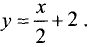
Ее график представлен на рис. 4.5.
Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство
видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.
2.Границей второй полуплоскости является прямая
Представим это уравнение в виде
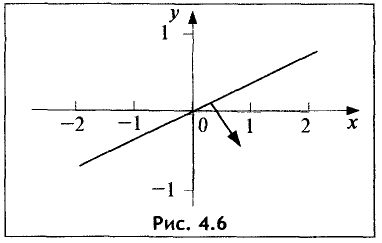
График исследуемой прямой представлен на рис. 4.6.
В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство 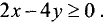
Видео:11. Прямая в пространстве и ее уравненияСкачать

Основные свойства выпуклого множества точек
Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.
Теорема:
Множество решений совместной системы т линейных
неравенств с двумя переменными
является выпуклым многоугольником (или выпуклой многоугольной областью).
Знаки некоторых или всех неравенств могут быть
Эту теорему для n переменных можно сформулировать
следующим образом.
Теорема:
Множество решений совместной системы m линейных
неравенств с n переменными
является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.
Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.
Область решений системы, удовлетворяющая условиям неотрицательности 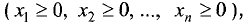
Пример:
Построить область решений и область допустимых
решений системы неравенств и определить координаты угловых точек области допустимых решений:
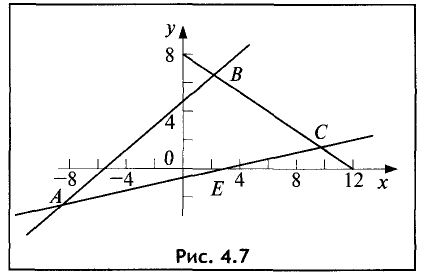
Решение:
Областью решений является треугольник ABC, представленный на рис. 4.7.
Сторона АВ треугольника, образованная границей первого неравенства системы, определяется уравнением прямой у = х + 5 .
Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство 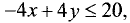




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📽️ Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

18. Расстояние от точки до прямой в пространствеСкачать

Изображение множества точек на координатной плоскости, удовлетворяющих уравнению.Скачать

Множества и операции над нимиСкачать

Уравнение плоскости. 11 класс.Скачать

Митио Каку - Физика невозможногоСкачать

16. Показать что прямые пересекаются и найти точку их пересечения в пространствеСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

Уравнение, которое меняет взгляд на мир [Veritasium]Скачать
![Уравнение, которое меняет взгляд на мир [Veritasium]](https://i.ytimg.com/vi/DH1cv0Rdf2w/0.jpg)
Что случилось над Азовским морем с самолетом ДРЛО А-50УСкачать

11 класс, 20 урок, Уравнение сферыСкачать

Что было до большого взрыва, когда конец вселенной и другие ответы на большие вопросы вселенной.Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение прямой в пространстве. 11 класс.Скачать

Математика это не ИсламСкачать