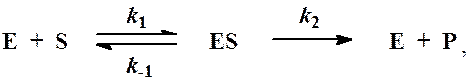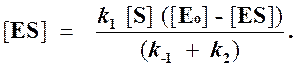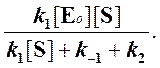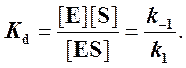Уравнение михаэлиса ментен квазиравновесное приближение и постулаты (3 видео)

Уравнение михаэлиса ментен квазиравновесное приближение и постулаты

Во многих случаях скорость реакции резко изменяется в присутствии специальных веществ — катализаторов. Катализаторы участвуют в реакции, но в результате ее не расходуются. Катализаторы биологических процессов, протекающих в живых организмах, представляют собой белковые молекулы, которые называют ферментами, или энзимами.

Простейшая схема ферментативного катализа включает обратимое образование промежуточного комплекса фермента (E) с реагирующим веществом (субстратом, S) и разрушение этого комплекса с образованием продуктов реакции (P):

Применение квазиравновесного приближения к этой схеме (при условии k₂ > k₁). Применение этого метода к простейшей схеме катализа дает уравнение Михаэлиса-Ментен:

, (7.2)

где w_max = k₂ . [E]₀ — максимальная скорость реакции (при бесконечно большой концентрации субстрата),

— константа Михаэлиса. Эта константа равна концентрации субстрата, при которой скорость реакции равна половине максимальной скорости. Типичные значения K_M — от 10 -6 до 10 -1 моль/л. Константу скорости k₂ иногда называют числом оборотов фермента. Она может изменяться в пределах от 10 до 10 8 мин -1 .

Уравнение (7.2) можно записать в других координатах, более удобных для обработки экспериментальных данных:

(7.2а)

(координаты Лайнуивера-Берка) или

. (7.2б)

Для определения параметров K_M и w_max по уравнениям (7.2а) и (7.2б) проводят серию измерений начальной скорости реакции от начальной концентрации субстрата и представляют экспериментальные данные в координатах 1/w₀ ё 1/[S]₀ или w₀ ё w₀/[S]₀.

Иногда течение ферментативной реакции осложняется присутствием ингибиторов — веществ, способных образовывать комплексы с ферментом или фермент-субстратным комплексом. Различают конкурентное, неконкурентное и смешанное ингибирование.

При конкурентном механизме ингибитор (I) конкурирует с субстратом за активные участки фермента. Простейшая кинетическая схема данного процесса имеет вид:

Применение квазистационарного приближения к комплексу ES и квазиравновесного приближения к комплексу EI с учетом уравнений материального баланса [E] + [ES] + [EI] = [E]₀ и [I] » [I]₀ дает для скорости реакции уравнение типа (7.2):

, (7.3)

где эффективная константа Михаэлиса связана с исходной концентрацией ингибитора:

; (7.3а)

Величину K_I = [E]. [I] / [EI], которая представляет собой константу диссоциации комплекса фермента с ингибитором, называют константой ингибирования. Таким образом, при конкурентном ингибировании увеличивается константа Михаэлиса, а максимальная скорость ферментативной реакции остается неизменной.

При неконкурентном механизме ингибитор обратимо связывает промежуточный комплекс фермента с субстратом. Простейшая кинетическая схема данного процесса имеет вид:

где предполагается, что константы диссоциации комплексов EI и ESI одинаковы: [E]. [I] / [EI] = [ES]. [I] / [ESI] = K_I. Применение квазистационарного приближения к комплексу ES и квазиравновесного приближения к комплексам EI и ESI с учетом уравнений материального баланса [E] + [ES] + [EI] + [ESI] = [E]₀ и [I] » [I]₀ дает для скорости реакции уравнение типа (7.2):

, (7.4)

где эффективная максимальная скорость связана с начальной концентрацией ингибитора выражением:

. (7.4а)

При неконкурентном ингибировании максимальная скорость реакции уменьшается, а константа Михаэлиса остается неизменной.

Смешанное ингибирование описывается более сложными кинетическими схемами. При смешанном ингибировании изменяются и константа Михаэлиса, и максимальная скорость ферментативной реакции.

Пример 7-1. Найдите константу Михаэлиса и максимальную скорость гидролиза аденозинтрифосфата, катализируемого миозином, по следующим кинетическим данным:

Решение. Уравнение Михаэлиса-Ментен в данных координатах имеет вид (7.2б), следовательно, точки пересечения с осями имеют координаты: (0;w_max) для оси ординат, (w_max/K_M;0) для оси абсцисс. Первая точка пересечения дает значение w_max = 2.1 . 10 -6 моль/(л. с). Вторая точка позволяет найти константу Михаэлиса: w_max/K_M = 14.6 . 10 -3 с -1 , K_M = 2.1 . 10 -6 / 14.6 . 10 -3 = 1.44 . 10 -4 моль/л.

Пример 7-2. Ферментативная реакция (K_M = 2.7 . 10 -3 моль/л) подавляется конкурентным ингибитором (K_I = 3.1 . 10 -5 моль/л). Концентрация субстрата равна 3.6 . 10 -4 моль/л. Сколько ингибитора понадобится для подавления реакции на 65%? Во сколько раз надо повысить концентрацию субстрата, чтобы уменьшить степень подавления до 25%?

Решение. 1) Конкурентное ингибирование описывается формулами (7.3) и (7.3а). 65%-ное подавление реакции означает, что скорость ингибируемой реакции составляет 35% от скорости реакции в отсутствие ингибитора:

откуда следует, что

В этой формуле известны значения K_M, K_I и [S]. Концентрация ингибитора равна:

6.5 . 10 -5 моль/л.

Уменьшение степени ингибирования до 25% означает, что скорость ингибируемой реакции составляет 75% от нормальной:

где в данном случае известны K_M, K_I и [I]₀. Отсюда можно выразить искомую концентрацию субстрата:

1.4 . 10 -2 моль/л.

Таким образом, для уменьшения степени ингибирования до 25% концентрацию субстрата надо увеличить в 1.4 . 10 -2 / 3.6 . 10 -4 = 40 раз.

7-1. Гидролиз ацетилхолина катализируется ферментом ацетилхолинэстеразой, число оборотов которой составляет 25000 с -1 . Сколько времени потребуется ферменту для расщепления одной молекулы ацетилхолина? (ответ)

7-2. Для некоторой ферментативной реакции константа Михаэлиса равна 0.035 моль/л. Скорость реакции при концентрации субстрата 0.110 моль/л равна 1.15 . 10 -3 моль/(л. с). Найдите максимальную скорость этой реакции.(ответ)

7-3. Начальная скорость окисления сукцината натрия в фумарат натрия под действием фермента сукциноксидазы была измерена для ряда концентраций субстрата:

0.0005

0.00033w . 10 6 , моль/(л. с)

Определите константу Михаэлиса данной реакции.(ответ)

7-4. Начальная скорость выделения O₂ при действии фермента на субстрат была измерена для ряда концентраций субстрата:

0.002w, мм 3 /мин

Определите константу Михаэлиса данной реакции.(ответ)

7-5. Найдите константу Михаэлиса и максимальную скорость каталитического разложения гидроперекиси тетралина по следующим кинетическим данным:

7-6. Найдите константу Михаэлиса и максимальную скорость каталитического окисления циклогексена трет-бутилпероксидом по следующим кинетическим данным:

7-7. Найдите константу Михаэлиса и максимальную скорость гидролиза карбобензилоксиглицилфенилаланина под действием карбоксипептидазы по следующим кинетическим данным:

7-8. Рассчитайте концентрацию неконкурентного ингибитора I (K_I = 2.9 . 10 -4 моль/л), необходимую для 90%-ного подавления ферментативной реакции.(ответ)

7-9. В некоторых случаях кинетические исследования ферментативных реакций проводят в условиях избытка фермента. Выведите уравнение Михаэлиса-Ментен, описывающее зависимость начальной скорости ферментативной реакции от начальных концентраций фермента и субстрата в системе

при условии, что концентрация фермента намного больше концентрации субстрата.(ответ)

*7-10. Рассмотрите механизм ферментативного катализа с двумя промежуточными комплексами:

Используя метод квазистационарных концентраций и уравнение материального баланса, покажите, что скорость реакции описывается уравнением типа Михаэлиса-Ментен (7.2). Найдите выражения для эффективной максимальной скорости и эффективной константы Михаэлиса через константы скорости отдельных стадий.(ответ)

7-11. Запишите уравнения конкурентного и неконкурентного ингибирования в координатах Лайнуивера-Берка. Представьте эти уравнения в графическом виде для трех разных начальных концентраций ингибитора (включая [I]₀ = 0). Объясните, как можно определить константу ингибирования.(ответ)

7-12. Запишите уравнения конкурентного и неконкурентного ингибирования в координатах w₀ w₀/[S]₀. Представьте эти уравнения в графическом виде для трех разных начальных концентраций ингибитора (включая [I]₀ = 0). Объясните, как можно определить константу ингибирования.(ответ)

*7-13. Рассмотрите схему неконкурентного ингибирования с разными константами диссоциации комлпексов:

Используя квазистационарное приближение для ES и квазиравновесное приближение для EI и ESI, найдите начальную скорость реакции. Как связаны максимальная скорость реакции и константа Михаэлиса с соответствующими величинами для неингибируемой реакции?(ответ)

Уравнение михаэлиса ментен квазиравновесное приближение и постулаты

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Содержание

Уравнение Михаэлиса-Ментен. Ингибирование ферментов
Страницы работы
Содержание работы
Ограничения кинетики Михаэлиса-Ментен
💡 Видео

Видео:Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать

Уравнение Михаэлиса-Ментен. Ингибирование ферментов

Страницы работы

Содержание работы

УРАВНЕНИЕ МИХАЭЛИСА —МЕНТЕН

Простейшей моделью для построения и обсуждения теорий ферментативной кинетики является кинетика односубстратных реакций. Хотя чаще всего в реакциях участвует не один, а большее число субстратов, реакцию можно рассматривать как односубстратную, если второй субстрат присутствует в очень большой концентрации. Большинство получаемых выводов можно использовать непосредственно при рассмотрении более сложных ферментативных реакций.

Как уже упоминалось, концентрация субстрата является одним из наиболее важных факторов, определяющих скорость ферментативной реакции.

В начале XX столетия Л. Михаэлисом и М. Ментен было предложено простейшее кинетическое выражение для скорости ферментативной односубстратной реакции.

Схема ферментативного процесса записывается следующим образом:

где Е — фермент; S — субстрат, подвергающийся ферментативной реакции; Р — образующийся в результате продукт;

Уравнение скорости ферментативной реакции, выведенное Михаэлисом и Ментен, предположивших, что превращение субстрата происходит только в переходном фермент-субстратном комплексе, основывается на двух предпосылках.

1. Реакция между ферментом и субстратом находится в равновесии. Это условие выполняется, если скорость распада комплекса на свободный фермент и субстрат значительно больше скорости распада его до свободного фермента и продукта (k_-1 >> k₂).

2. Концентрация свободного субстрата остается практически постоянной в течение начального периода реакции, тогда концентрация субстрата [S] может быть принята равной полной концентрации субстрата [S_o]. Это условие выполняется, если полная концентрация субстрата значительно больше полной концентрации фермента, как это обычно имеет место при кинетических исследованиях.

При высокой каталитической активности фермента реальное значение концентрации фермент-субстратного комплекса отличается от его значения в условиях равновесия. Для анализа кинетики реакции с учетом этого обстоятельства Бриггс и Холдейн предложили дополнить теорию Михаэлиса — Ментен условием стационарного состояния.

Согласно этому условию в любой момент реакции скорости образования и распада комплекса ES практически равны, так что концентрация комплекса [ES] может считаться постоянной (квазистационарной) в течение короткого периода времени, необходимого для измерения скорости. В течение более продолжительного периода времени концентрация комплекса [ES] будет изменяться по ходу реакции в связи с падением концентрации субстрата, но скорость изменения ее всегда будет существенно меньше, чем скорость ферментативной реакции.

Для стационарного состояния, при котором

k₁[E][S] – (k_-1 + k₂)·[ES] = 0

(1)

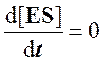
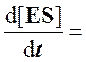
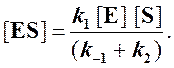
Из уравнения материального баланса для фермента

где [E_o] ─ его начальная концентрация, а [E] ─ текущая концентрация свободного, не связанного в фермент-субстратный комплекс белка, можно записать

и подставить в выражение (1):

Отсюда концентрация ES равна

[ES] =

Тогда начальная скорость ферментативной реакции, измеряемая по скорости образования продукта Р, равна

(2)

(константа Михаэлиса),

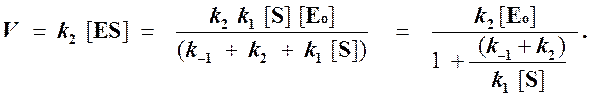
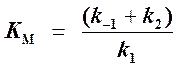
то выражение (2) можно записать в следующем виде:

(3)

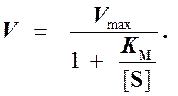
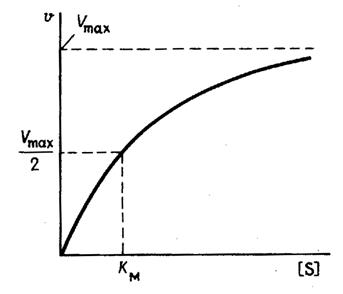
Выражение (3) называется уравнением Михаэлиса —Ментен и описывает зависимость скорости односубстратной ферментативной реакции от концентрации субстрата. Из этого уравнения видно, что при увеличении концентрации субстрата (при неизменной концентрации фермента) скорость реакции стремится к предельному значению, равному V_max.

При выводе уравнения Михаэлиса — Ментен, кроме вышеперечисленных, принимается во внимание еще несколько не совсем реальных допущений, таких как:

1) отсутствие образования значимого количества комплекса ЕР и других форм фермента;

2) необратимость второй стадии реакции, т. е. образования продукта Р. Это связано с тем, что мы рассматриваем только начальную скорость процесса, когда обратной реакцией из-за фактического отсутствия продукта еще можно пренебречь;

3) связывание с активным центром на каждой субъединице фермента только одной молекулы субстрата;

4) использование для всех реагирующих веществ вместо активностей их концентраций.

Если k₂ значительно меньше k_-1, то этим членом в выражении константы Михаэлиса можно пренебречь, и К_M становится равной отношению 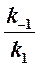, а это есть К_d (константа диссоциации фермент-субстратного комплекса):

Таким образом, являясь аналогом константы диссоциации фермент-субстратного комплекса ES, константа Михаэлиса характеризует сродство фермента к субстрату. Чем ниже К_M, тем выше сродство.

На рис. 1 приведено графическое изображение уравнения Михаэлиса — Ментен.

Рис. 1.Зависимость скорости ферментативной реакции от концентрации субстрата

Видео:USMLE Step 1 - Фармакология: кинетика ферментов | уравнение Михаелиса - Ментена и не толькоСкачать

Ограничения кинетики Михаэлиса-Ментен

Михаэлис и Ментен вывели уравнение с учетом двух предположений (быстро устанавливающееся равновесие и избыток субстрата). Позднее было показано, что уравнение справедливо, то есть хорошо описывает реакцию, при выполнении всех следующих условий. 7 основных постулатов для выполнения уравнения Михаэлиса-Ментен.

1. В ходе реакции образуется кинетически устойчивый фермент-субстратный комплекс.

2. Определяемая с помощью уравнения константа Кs является константой диссоциации фермент-субстратного комплекса: это справедливо, только если k₂ -2 до 10 -7 , чем меньше Кm, тем активнее фермент. При V=1/2Vmax, имеем Km = [S]. Однако, определение Vmax затруднительно по асимптоте. Для устранения этого неудобства ЛАЙНУИВЕР и БЭРК приравняли обратные зависимости левой и правой частей уравнения.

Графическое выражение для скорости реакции в координатах Лайнуивера-Бэрка имеет вид прямой линии, отсекающей на оси Х значение -1/Km, а на оси Y- значение 1/V max:

48.Физический смысл основных кинетических характеристик ферментативной реакции (Vmax, К_m).

Ур михаэлиса имеет вид: ; (V_max– максимальная скорость реакции при полном насыщении фермента субстратом) и носит несколько ограниченный характер. Поэтому были предприняты попытки усовершенствовать его. Так, было предложено уравнение Бриггса-Холдейна: где К_m представляет собой константу Михаэлиса Для определения численного значения К_m обычно находят ту концентрацию субстрата, при которой скорость ферментативной реакции v составляет половину от максимальной V_max, т.е. если v = 1 /₂ V_maх. Подставляя значение v в уравнение Бриггса–Холдейна, получаем: разделив обе части уравнения на V_mах, получим

Таким образом, константа Михаэлиса численно равна концентрации субстрата (моль/л), при которой скорость данной ферментативной реакции составляет половину от максимальной. Предельное значение, к которому стремится гипербола — Vmax данной реакции — характеризует максимальную работоспособность фермента: Vmax=k+2 x [E]. Таким образом, Vmax — это предел, к которому стремится скорость реакции при бесконечном повышении концентрации субстрата. kм — это константа Михаэлиса. Она численно равна той концентрации субстрата, при которой скорость реакции составляет половину от максимального значения. Эта кривая описывается уравнением Михаэлиса-Ментен. Физический смысл Км заключается в том, что она представляет собой константу равновесия между двумя реакциями, приводящими к распаду фермент-субстратного комплекса и той реакцией, которая ведет к образованию этого комплекса. Ks — субстратная константа. Характеризует константу равновесия 1-го этапа ферментативной реакции. Следовательно, Км обычно тоже довольно близка к Кs. Следовательно, Км, как и Кs, характеризует сродство субстрата к данному ферменту. Но экспериментально определить k-1 и k+2 очень трудно, поэтому трудно определить и Кs. А вот Км можно просто определить, используя координаты Лайнуивера-Бэрка. С помощью Км можно характеризовать сродство данного фермента к данному субстрату. Чем меньше Км, тем больше сродство фермента к данному субстрату, а значит тем больше равновесие первого этапа ферментативной реакции сдвинуто вправо — в сторону образования фермент-субстратного комплекса. Значит, будут созданы наилучшие условия для протекания и второго этапа ферментативного процесса. При таких условиях для достижения эффективного превращения субстрата требуется малая концентрация субстрата. Значит, и Vmax теоретически может быть достигнута при малых количествах субстрата. Если Км высока, то это означает, что сродство фермента к такому субстрату низкое и реакция при небольших концентрациях субстрата протекает неэффективно. Км и Vmax — это две кинетические константы, с помощью которых можно характеризовать эффективность работы фермента, в том числе и in vivo.