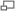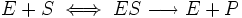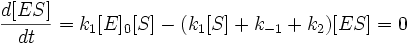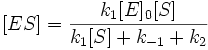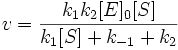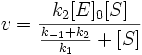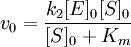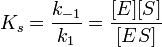Уравнение михаэлиса ментен и его графическое выражение

Уравнения Михаэлиса-Ментен и Лайнуивера-Берка

Общую теорию ферментативной кинетики и зависимость активности фермента от субстрата.описали Л.Михаэлис и М.Л.Ментен, выразив его в своем уравнении. Бриггс и Холдейн усовершенствовали их уравнение, введя введя в него константу Михаэлиса (Km), определяемую экспериментально.

Уравнение Михаэлиса-Ментен показывает взаимосвязь максимально возможной скорости, реальной скорости реакции, константы Михаэлиса и концентрации субстрата. Так как пользоваться графиком, построенным в прямых координатах V и [S] для точных расчетов неудобно, то Г.Лайнуивер и Д.Бэрк преобразовали уравнение Бриггса–Холдейна в обратные координаты.

Уравнение Михаэлиса-Ментен

Уравнение Лайнуивера-Бэрка

На самом деле уравнение Михаэлиса-Ментен в данном виде предложили Бриггс и Холдейн, но в честь основоположников оно носит название Михаэлиса-Ментен.

Выделяют три основных решения уравнения Михаэлиса-Ментен:

1. Концентрация субстрата равна величине константы Михаэлиса ([S] = Km).
В этом случае, решая уравнение Михаэлиса-Ментен, получаем, что скорость реакции V будет равна половине максимальной Vmax.(V = ½ Vmax).

В математическом смысле Km соответствует концентрации субстрата при которой скорость реакции равна половине максимальной. Ее биологический смысл заключается в характеристике сродства фермента к субстрату, а именно: увеличение величины Кm означает снижение сродства фермента к субстрату.

2. Концентрация субстрата значительно больше Km ([S] >> Km). В этом случае величиной Km можно пренебречь, при решении получим, что скорость реакции максимальна (плато на графике).

3. Концентрация субстрата значительно меньше Km ([S]

Видео:Кинетика. О чем говорят графики. БиохимияСкачать

Уравнение Михаэлиса — Ментен

Диаграмvа скорости реакции V как функции от концентрации [S].

Уравне́ние Михаэ́лиса — Ме́нтен — основное уравнение ферментативной кинетики, описывает зависимость скорости реакции, катализируемой ферментом, от концентрации субстрата и фермента. Простейшая кинетическая схема, для которой справедливо уравнение Михаэлиса:

Уравнение имеет вид:

,

· — максимальная скорость реакции, равная ;

· — константа Михаэлиса, равная концентрации субстрата, при которой скорость реакции составляет половину от максимальной;

· — концентрация субстрата.

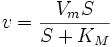
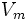
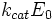
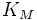
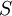
Вывод уравнения

Вывод уравнения был впервые предложен Бриггсом и Холдейном. Вывод уравнения скорости ферментативной реакции, описываемой схемой Михаэлиса-Ментен.

Обозначения констант скоростей:

k₁ — константа скорости реакции образования фермент-субстратного комплекса из фермента и субстрата

k_-1 — константа скорости реакции диссоциации фермент-субстратного комплекса на фермент и субстрат

k₂ — константа скорости реакции превращения фермент-субстратного комплекса в фермент и продукт

Для фермент-субстратного комплекса применим метод квазистационарности, так как в подавляющем большинстве реакций константа скорости превращения фермент-субстратного комплекса в фермент и продукт много больше, чем константа скорости образования ферменто-субстратного комплекса из фермента и субстрата. Иными словами:

Учтем тот факт, что фермент, изначально находившийся только в свободной форме, в процессе реакции находится как в виде фермент-субстратного комплекса, так и в виде молекул свободного фермента. Таким образом:

Преобразуем это к виду:

И подставим в первое уравнение. После раскрытия скобок и группировки слагаемых получим следующее:

Выразим отсюда концентрацию фермент-субстратного комплекса:

Скорость ферментативной реакции в целом (то есть скорость образования продукта) представляет собой скорость распада фермент-субстратного комплекса по реакции первого порядка с константой k₂:

Подставим в эту формулу выражение, которое мы получили для концентрации ES. Получим:

Разделим числитель и знаменатель на k₁. В результате:

Выражение в знаменателе — (k_-1+k₂)/k₁ — называется константой Михаэлиса (K_m). Это кинетическая константа (с размерностью концентрации), которая равняется такой концентрации субстрата, при которой скорость ферментативной реакции составляет половину от максимального значения.

Для начальной стадии реакции можно пренебречь уменьшением концентрации субстрата. Тогда выражение для начальной скорости реакции будет выглядеть так:

Если k_-1>k₂, то на первой стадии ферментативной реакции с течением времени устанавливается равновесие (квазиравновесный режим протекания реакции), и в выражение для скорости ферментативной реакции входит уже не константа Михаэлиса, а субстратная константа K_S, характеризующая взаимодействие фермента с субстратом в равновесных условиях:

;

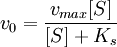
По значению K_S можно судить о химическом сродстве субстрата к ферменту.

Металлоферменты и ферменты, активируемые металлами
Металлоферменты содержат определенное количество ионов металлов, имеющих функциональное значение и остающихся связанными с молекулой фермента в ходе его очистки. Ферменты, активируемые металлами, связывают последние менее прочно, но для своей активности требуют добавления металлов в среду. Таким образом, разграничение между металлоферментами и ферментами, активируемыми металлами, основано на сродстве данного фермента к иону «своего» металла. Механизмы, основанные на участии ионов металлов в катализе, в обоих случаях, по-видимому, сходны.
Тройные комплексы фермент—металл — субстрат
Для тройных (трехкомпонентных) комплексов, включающих каталитический центр (Enz), ион металла (М) и субстрат (S) со стехиометрией 1:1:1, возможны четыре различных схемы образования:
Enz—S—М М —Enz—S
Комплекс с мостиковым Комплекс с мостиковым субстратом ферментом
М
Enz—M—S Enz|
S
Простой комплекс с Циклический комплекс
мостиковым металлом с мостиковым металлом
В случае ферментов, активируемых металлами, реализуются все четыре схемы. Для металлофермен-тов образование комплекса Enz—S—М невозможно, иначе они не могли бы удерживать металл в процессе очистки (они находятся в форме Enz — — М). Можно сформулировать три общих правила.
1. Большинство (но не все) киназ (АТР:фосфо-трансферазы) образуют комплексы с мостиковым субстратом типа Enz—нуклеозид—М.
2. Фосфотрансферазы, использующие в качестве субстрата пируват или фосфоенолпируват, другие ферменты, катализирующие реакции с участием фосфоенолпирувата, а также карбоксилазы образуют комплексы с мостиковым металлом.
3. Данный фермент может быть способен к образованию мостикового комплекса одного типа с одним субстратом и другого типа — с другим.
Комплексы с мостиковым ферментом(М —Enz—S)
Металлы в комплексах с мостиковым ферментом, по-видимому, выполняют структурную роль, поддерживая активную конформацию (примером служит глутаминсинтаза), или образуют мостик с другим субстратом (как в пируваткиназе). В пиру-ваткиназе ион металла играет не только структурную роль, но и удерживает один из субстратов (АТР) и активирует его:
А
Пируваткиназа—АТР
Креатин.
Комплексы с мостиковым субстратом
Образование тройных комплексов с мостиковым субстратом, которое наблюдается при взаимодействии ферментов с нуклеозидтрифосфатами, по-видимому, связано с выстеснением Н₂0 из координационной сферы металла, место которой занимает АТР:
АТР- + M(H₂0) 2+ _fi г± АТР—М(Н₂0) 2 + ЗН₂0.
Затем субстрат связывается с ферментом, образуя тройной комплекс:
АТР—М(Н₂0) 2 :, + Enz 2 :_v
В фосфотрансферазных реакциях ионы металлов, как полагают, активируют атомы фосфора и образуют жесткий полифосфат-адениновый комплекс в соответствующей конформации, который включается в состав активного четырехкомпонентного комплекса.
Комплексы с мостиковым металлом
м
Enz-M-SnnnEnz |
S
Кристаллографические данные, а также анализ первичной структуры показывают, что в активных центрах многих белков в связывании металла участвует остаток гистидина (примерами служат кар-боксипептидаза А, цитохром с, рубредоксин, мет-миоглобин и метгемоглобин; см. гл. 6). Лимитирующей стадией образования бинарных (двухкомпо-нентных) комплексов Enz—М во многих случаях является вытеснение воды из координационной сферы иона металла. Активация многих пептидаз ионами металла является медленным процессом, длящимся несколько часов. Среди таких металлоферментов особое значение в живых системах имеют цитохромы и гемсодержащие ферменты, активными группировками которых служат железопорфириновые комплексы ( см. стр. [1]

Во многих металлоферментах, особенно катализирующих окислительно-восстановительные реакции, присутствуют именно металлы с переменной валентностью, действующие как акцепторы водорода, например железо, медь, марганец, молибден. Известно, что для активации таких ферментов, как ксантиноксидаза или нитроредуктаза, молибден должен быть в шестивалентном состоянии. [2]

Карбоксипептидаза — это металлофермент, содержащий один атом цинка на молекулу белка. Карбоксипептидаза катализирует гидролиз С-концевой пептидной связи в белках и олигопеп-тидах и сложных эфиров а-оксикислот. По данным рентгеноструктурного анализа Карбоксипептидаза представляет собой глобулярный белок, в котором содержится один атом цинка, координированный двумя остатками гистидина. Кроме того, в состав активного центра входят карбоксильная ( Glu-270), фенольная ( Туг-248) и гуанидиновая ( Arg-145) группы. [3]

Ингибирует широкий набор металлоферментов, включая гидроге-назу и гемоглобины ( при низких конц. СО-инги-бирование, обратимое под действием света, характерно для цитохромокси-дазы и др. гемсодержащих белков. Карбонилы Си и др. металлов не чувствительны к свету. Моноксид углерода сильно токсичен для многих живых тканей и микроорганизмов. [4]

СОД относится к металлоферментам, у которых в активном центре происходит восстановление и окисление иона металла. [5]

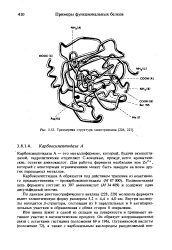Трехмерная структура химотрипсина.

Карбоксипептидаза А — это металлофермент, который, будучи экзопепти-дазой, гидролитически отщепляет С-концевые, прежде всего ароматические, остатки аминокислот. Для работы фермента необходим ион Zn2, который с некоторыми ограничениями может быть замещен на ионы других переходных металлов. [6]

Сравнительное изучение каталитических свойств различных металлоферментов в начале было главным образом ограничено оценкой их относительной каталитической активности. Однако детальное изучение катализа и связывания лиганда для серии металлоферментов может пролить свет на роль иона металла, если при отсутствии каталитической активности сохраняется связывание металла. [7]

Прочность связи фосфата с металлоферментом удивительно велика. Константа устойчивости комплекса, равная около 106 М 1 [51, 63, 76], выше, чем можно было бы ожидать для взаимодействия НРО f — и иона двухвалентного металла. Вероятно, вблизи иона цинка находится еще один катионный центр связывания, например протон аминогруппы боковой цепи аминокислоты, взаимодействующий с кислородными атомами фосфата. Образование фосфорилфермента при реакции с субстратом и НРО можно считать твердо установленным. После разрушения белка фосфат оказывается присоединенным к серину. Отсюда делается вывод о том, что в активном центре вблизи иона цинка находится остаток серина, ориентация которого делает возможной его атаку по фосфорильному атому присоединенного производного фосфата. Вполне вероятно, что фосфорильная группа, присоединенная к серину, сохраняет связь с ионом цинка. [8]

ЭКВ отчетливо проявляются в свойствах металлоферментов. Металлы служат кофакторами многих ферментов — в большинстве классов ферментов имеются металлозависимые. [9]

В части IV рассмотрены структуры металлоферментов и механизмы, посредством которых ионы металлов принимают участие в ферментативной активности, в частности, в разрыве связей. [10]

Малер [8] подчеркивает различия между металлоферментами, в которых металл прочно связан с белком ( по существу необратимо), и ферментами, активированными металлами, в которых связь металла с белком слаба и легкообратима. [11]

В настоящее время известно более 100 истинных металлоферментов, участвующих в большинстве реакций клеточного метаболизма. Многие из них передают электроны за счет металлов с переменной валентностью. В этом случае можно постулировать, что металл принимает непосредственное участие в осуществлении каталитического акта. [12]

Ферменты окислительно-восстановительного действия являются чаще всего металлоферментами, так как в качестве компонентов каталитически активных центров этих ферментов служат металлы. В истинных металлоферментах металл прочно связан в строго определенных стехиометрических соотношениях с теми или иными химическими группировками апофермента или со специальной группой небелковой природы. [13]

В этих же органах и тканях находятся соответствующие металлоферменты или ферменты, активируемые тем или иным металлом. Так, для меди, цинка, молибдена, селена, марганца критическим органом является печень; для марганца, кобальта — также и щитовидная железа; для кадмия и цинка — мужские половые железы и почки; для бериллия — костная ткань. Полагают также, что распределение металлов внутри клетки коррелирует с содержанием в ней металлосодержащих ферментов

Дата добавления: 2017-01-13 ; просмотров: 4690 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать

Кинетика и термодинамика ферментативных реакций (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Министерство образования и науки Российской Федерации

Сибирский федеральный университет

Кинетика и термодинамика ферментативных реакций

к практическим занятиям

Специальность 020208.65 — Биохимия

Кинетика и термодинамика ферментативных реакций: Сборник задач к практическим занятиям /[Текст] / сост. . – Красноярск: Сиб. федер. ун-т, 2012. – 64 с.

Сборник задач по курсу «Кинетика и термодинамика ферментативных реакций» составлен в соответствии с программой курса и является учебно-методическим руководством по решению задач по кинетическим свойствам ферментов.

В учебном пособии представлены четко структурированные задачи по основному разделу курса «Кинетика ферментативных реакций» разной степени сложности. Предназначено для студентов биологических и медико-биологических специальностей университетов.

В ферментативной кинетике концепция стационарности применима к концентрациям связанных с ферментом интермедиатов. Когда фермент смешивается с избытком субстрата наблюдается начальный период, известный как предстационарное состояние, в течение которого концентрации этих интермедиатов достигают стационарного уровня. По достижении интермедиатами стационарных концентраций скорость реакции относительно медленно изменяется со временем и именно в данный период традиционно измеряют скорости энзиматических реакций.

Стационарное состояние является аппроксимацией, поскольку субстрат постепенно превращается в ходе эксперимента. Но, принимая во внимание, что измерения осуществляются за короткий промежуток времени, когда концентрация субстрата изменяется незначительно, стационарное состояние является хорошей аппроксимацией. Хотя изучение предстационарной кинетики позволяет анализировать механизмы ферментативного катализа, стационарная кинетика более важна для измерения каталитической активности фермента при стационарных состояниях в клетке.

Раздел 1. Уравнение Михаэлиса-Ментен

Браун (Brown A. J.) и затем В. Анри (Henri V.) в начале ХХ века высказали предположение о том, что в основе ферментативной реакции лежит обратимое взаимодействис субстрата с ферментом с образованием комплекса, который далее распадается с образованием продуктов реакции и регенерацией исходного фермента. Эта гипотеза была далее развита в работах Михаэлиса (L. Michaelis) и Ментен (M. L. Menten) (1913 г.) и позднее – Бригсом (G. E. Briggs) и Холденом (J. B.S. Haldane) (1925 г.).

Кинетическую схему простейшей односторонней ферментативной реакции превращения одного субстрата в продукт можно представить следующим образом:

(1.1)

Ферментативная реакция протекает в два этапа. На первом этапе фермент и субстрат образуют фермент-субстратный комплекс ES. Этот этап является быстрым и обратимым, он не сопровождается какими-либо химическими изменениями субстрата. Константы скорости реакции образования фермент-субстратного комплекса и обратного его распада равны соответственно k+1 и k-1. В образовании фермент-субстратного комплекса (ФСК, комплекс Михаэлиса) принимают участие нековалентные взаимодействия.

Каталитический процесс осуществляется на втором этапе реакции с константой первого порядка k+2 (kcat, число оборотов фермента). Комплекс Михаэлиса распадается с образованием конечного продукта реакции Р и регенерацией исходного фермента. Распад фермент-субстратного комплекса может происходить по-разному: в данной кинетической схеме он распадается в одну стадию, но в других случаях этих стадий может быть несколько.

Исходя из уравнения (1), можно расписать уравнения для скоростей отдельных стадий реакции.

Скорость образования фермент-субстратного комплекса:

.

Скорость обратной реакции (диссоциации комплекса на исходные вещества):

.

Скорость распада комплекса ES с образованием продуктов реакции и регенерацией фермента:

.

Стационарное течение процесса возможно тогда, когда концентрация субстрата существенно превосходит концентрацию фермента ([S]>> [E]). В этом случае распад комплекса ES по реакциям (+2) и (-1) уравновешивается его образованием по реакции (+1). Поэтому для условия стационарности можно записать:

.

Обозначив общую концентрацию фермента через [E]0, при условии, что [E]0 = [E] + [ES], преобразуем предыдущее уравнение

.

Откуда концентрация фермент-субстратного комплекса будет равна

.

,

.

Скорость ферментативной реакции, измеряемая согласно схеме (1) по образованию продукта реакции Р из комплекса ES, может быть выражена следующим образом

.

Подставляя в это выражение найденное значение [ES], получаем

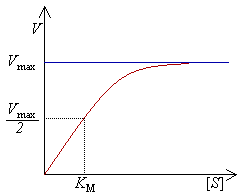
Данное уравнение отражает зависимость скорости ферментативной реакции от концентрации фермента и субстрата. Константа Км носит название константы Михаэлиса и имеет размерность концентрации субстрата. Уравнение (2) свидетельствует, что зависимость скорости ферментативной реакции от концентрации субстрата при [E]0=const является гиперболической функцией (рис. 1.1).

Рис.1.1. Зависимость скорости ферментативной реакции от концентрации субстрата

Кривая представляет собой равнобочную гиперболу. При достаточно малых концентрациях субстрата, когда [S] > Км, можно принять, что Км + [S] ≈ [S], и тогда

а реакция имеет нулевой порядок по отношению к субстрату. Следовательно, при достижении определенной концентрации субстрата скорость ферментативной реакции достигает максимального значения Vmax и при дальнейшем увеличении концентрации субстрата не изменяется.

Смысл такого рода зависимости очевиден: скорость ферментативной реакции определяется в целом концентрацией фермент-субстратного комплекса и при малых концентрациях субстрата концентрация комплекса Михаэлиса пропорциональна [S], тогда как при избытке субстрата фактически весь фермент находится в форме ES. Дальнейшее повышение концентрации субстрата не приводит к увеличению [ES].

С учетом приведенного выше выражения, окончательное уравнение зависимости скорости ферментативной реакции от концентрации фермента и субстрата приобретает вид

. (1.3)

Уравнение (3) является фундаментальным уравнением ферментативной кинетики и обычно называется уравнением Михаэлиса-Ментен.

Скорость реакции приближается к максимальной достаточно медленно, и даже при [S]= 10Км, величина скорости достигает только 0,91 Vmax. В связи с этим значение максимальной скорости очень часто трудно измеримо и его приходится рассчитывать из скоростей, наблюдаемых при концентрациях субстрата ниже насыщающих.

1.1. Характеристика кинетических констант

В уравнении Михаэлиса есть два кинетических параметра, имеющих важное значение для характеристики любого фермента. Это константа Михаэлиса и максимальная скорость реакции. Константа Михаэлиса определяется соотношением констант (k—1+k+2/k+1), а величина Vmax, называемая максимальной скоростью, ‒ произведением k+2 [E]0.

Константа Михаэлиса численно равна концентрации субстрата, при которой начальная скорость ферментативной реакции равна половине максимальной. Высокое сродство фермента к субстрату характеризуется низкой величиной Кm и наоборот, низкое сродство – высокой величиной Км.

Величина Vmax не является фундаментальной характеристикой фермента, поскольку зависит от его концентрации. Если концентрация фермента известна, то целесообразно ввести величину kcat – каталитическую константу (или число оборотов фермента), определяемую выражением Vmax/[E]0. Для механизма Михаэлиса kcat идентична k+2, однако в общем случае лучше пользоваться менее определенным обозначением, а именно kcat.

Константу kкат называют еще «числом оборотов» поскольку она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 с. Отношение констант kcat/Км называют константой специфичности фермента.

1.2. Методы определения Км и Vmax

Константу Михаэлиса можно определить из графика Михаэлиса (рис.1.1), найдя графическим способом максимальную скорость и соответствующую величину концентрации субстрата, при которой скорость ферментативной реакции будет вдвое меньше Vmax. Эта величина [S] и будет Км. Таким способом можно определить только приблизительную величину константы Михаэлиса из-за трудности точного графического определения Vmax.

Более удобными являются методы, в которых осуществлена линеаризация уравнения Михаэлиса-Ментен, т. е. гиперболическая зависимость v от [S] переведена в линейную.

Для того чтобы построить такой график, необходимо определить в одинаковых условиях при различных концентрациях субстрата и [E]= const начальные скорости ферментативной реакции.

Метод Лайнуивера-Берка. Один из способов линеаризации уравнения Михаэлиса-Ментен предложили Лайнуивер и Берк (Lineweaver H., Burk D.)). Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения (), в результате чего оно преобразуется в уравнение вида

согласно которому между величинами, обратными начальной скорости (1/v, v-1) и концентрации субстрата (1/[S], [S]-1) соблюдается линейная зависимость, если механизм реакции подчиняется изложенным выше представлениям (рис.1.2).

Рис. 1.2. График зависимости 1/v от 1/[S] (график Лайнуивера-Берка)

Экспериментальная прямая пересекает ось абсцисс в точке (-1/[S] = 1/Км), а ось ординат – в точке (1/v = 1/Vмах). Тангенс угла наклона равен Км/Vмах. Этим широко пользуются для определения параметров Км и Vмах, характеризующих связывающую и каталитическую функции ферментов.

Метод Хайнса-Вульфа. В этом случае преобразуется уравнение Лайнуивера-Берка путем умножения правой и левой частей на концентрацию субстрата.

Графическая зависимость приведена на рис.1.3.

Рис. 1.3. График зависимости [S]/v от [S] (график Хайнса-Вульфа)

Это прямая с наклоном 1/Vmax, отсекающая на осях [S]/v и [S] отрезки Км/ Vmax и – Км соответственно.

Метод Иди-Хофсти. При одном из таких графических преобразований в так называемом графике Иди-Хофсти (pиc.2.3.5) строят график зависимости v от v/[S]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует Vmax, а тангенс угла наклона равен – Km. Данный способ линеаризации приведен на рис. 1.4.

Рис. 1.4. График зависимости v от v/[S] (график Эди-Хофсти)

Метод Эйзенталя и Корниш-Боудена. Много позднее Эйзенталь и Корниш-Боуден предложили иной метод графического представления результатов исследования кинетики ферментативных реакций – так называемый прямой линейный график. Уравнение Михаэлиса-Ментен они преобразовали в виде зависимости Vmax от Км:

Для любой пары значений [S] и v можно построить зависимость Vmax от Км. Она представляет прямую с наклоном, равным v/[S], и отрезками, отсекаемыми на осях Км и Vmax, соответственно равными – [S] v. Если провести прямые для нескольких пар значений [S] и v, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения Vmax от Км, удовлетворяющие всем парам значений [S] и v (рис.1.5).

Рис.1.5. Определение кинетических констант – Км и Vmax по методу Эйзенталя и Корниш-Боудена

Преимущества такого графика очевидно: для его построения не требуется никаких расчетов, он позволяет очень просто выявить ошибочные данные (такие прямые будут выпадать из основной совокупности прямых).

Уравнение Михаэлиса лежит в основе всех кинетических исследований ферментативных реакций, так как оно позволяет рассчитать количественные характеристики ферментов и проводить анализ их ингибирования. Величины Кm и Vmax являются важнейшими характеристиками ферментов и их можно определить, используя линеаризованные формы уравнения Михаэлиса-Ментен.

Графические методы для определения Vmax и Кm не являются оптимальными. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью компьютерных программ.

1.3. Задачи к разделу 1

Задача 1.1.. Определить кинетические параметры реакции, катализируемой фосфоглюкомутазой, исходя из данных, приведенных в табл.1.

📺 Видео

USMLE Step 1 - Фармакология: кинетика ферментов | уравнение Михаелиса - Ментена и не толькоСкачать

ФЕРМЕНТЫ 5.Основы ферментативного катализа. Кинетика ферментативных реакций.Скачать

ФЕРМЕНТАТИВНАЯ КИНЕТИКА: Занятие 1. Вывод уравнения Михаэлиса-МентенСкачать

Ферментативная кинетикаСкачать

Асеев В. В. - Основы энзимологии - Ферментативная кинетика Уравнение Михаэлиса-МентенСкачать

Разбираем Michaelis-Menten and Lineweaver-Burk plots.Скачать

Лекция 4 Ферменты Кинетика, ингибирование, изоферментыСкачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать

ЛЕКЦИЯ №10 || Химическая кинетика || Лимитирующая стадия (пример), Катализ, схема Михаэлиса – МентенСкачать

Гладилин А.К. - Введение в специальность - 10. Ферментативная кинетикаСкачать

Асеев В. В. - Основы энзимологии - Кинетика ферментативных реакцийСкачать

Лекция 11 || 2021 || Схема Михаэлиса-Ментен (завершение), гетерогенный катализСкачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Лекция 11.11.20 | Схема Михаэлиса-Ментен (завершение), гетерогенный катализ | Химическая кинетикаСкачать

Лекция 10 || 2021 || Параллельные реакции (завершение), катализ, схема Михаэлиса-Ментен (начало)Скачать

Обратимость и необратимость химических реакций. Химическое равновесие. 1 часть. 9 класс.Скачать

1 Решение задачи графическим и аналитическим методомСкачать

Асеев В. В. - Основы биохимии - ФерментыСкачать