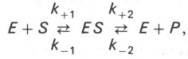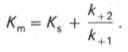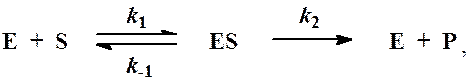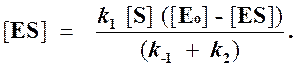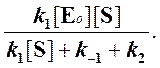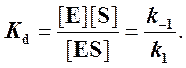Видео:Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать
Зависимость фермента от количества субстрата описывает ферментативная кинетика
Уравнения Михаэлиса-Ментен и Лайнуивера-Берка
Общую теорию ферментативной кинетики и зависимость активности фермента от субстрата.описали Л.Михаэлис и М.Л.Ментен, выразив его в своем уравнении. Бриггс и Холдейн усовершенствовали их уравнение, введя введя в него константу Михаэлиса (Km), определяемую экспериментально.
Уравнение Михаэлиса-Ментен показывает взаимосвязь максимально возможной скорости, реальной скорости реакции, константы Михаэлиса и концентрации субстрата. Так как пользоваться графиком, построенным в прямых координатах V и [S] для точных расчетов неудобно, то Г.Лайнуивер и Д.Бэрк преобразовали уравнение Бриггса–Холдейна в обратные координаты.
Уравнение Михаэлиса-Ментен
Уравнение Лайнуивера-Бэрка
На самом деле уравнение Михаэлиса-Ментен в данном виде предложили Бриггс и Холдейн, но в честь основоположников оно носит название Михаэлиса-Ментен.
Выделяют три основных решения уравнения Михаэлиса-Ментен:
1. Концентрация субстрата равна величине константы Михаэлиса ([S] = Km).
В этом случае, решая уравнение Михаэлиса-Ментен, получаем, что скорость реакции V будет равна половине максимальной Vmax.(V = ½ Vmax).
В математическом смысле Km соответствует концентрации субстрата при которой скорость реакции равна половине максимальной. Ее биологический смысл заключается в характеристике сродства фермента к субстрату, а именно: увеличение величины Кm означает снижение сродства фермента к субстрату.
2. Концентрация субстрата значительно больше Km ([S] >> Km). В этом случае величиной Km можно пренебречь, при решении получим, что скорость реакции максимальна (плато на графике).
3. Концентрация субстрата значительно меньше Km ([S]
Видео:Кинетика. О чем говорят графики. БиохимияСкачать
Вывод уравнения Михаэлиса-Ментен.
Полный математический анализ ферментативной реакции приводит к сложным уравнениям, не пригодным для практического применения. Наиболее удобной оказалась простая модель, разработанная в 1913 г Михаэлисом и его сотрудницей Ментен. Она объясняет характерную гиперболическую зависимость скорости реакции при постоянной концентрации фермента от концентрации субстрата и позволяет получать константы, которые количественно характеризуют эффективность фермента.
Модель Михаэлиса-Ментенисходит из того, что вначале субстрат (S) обратимо образует с ферментом (E) комплекс (ЕS), который ,быстро превращается в продукт Р, что можно выразить следующей схемой:
Математическая обработка этой системы уравнений с использованием закона действующих масс и уравнения материального баланса позволяет вывести уравнение, названное в честь авторов уравнением Михаэлиса–Ментен, выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:
Вывод уравнения Михаэлиса-Ментен:
Скорость прямой реакции образования ES — Vпр = K+1[E][S] 1
Скорость обратной реакции — Vобр = К-1[ES] 2
В стационарном состоянии, т.е. когда концентрация ES постоянна скорость прямого процесса равна скорости обратного — Vпр = Vобр или K+1[E][S] = К-1[ES]
[E][S]/[ES] = K-1/K+1 = Кs – константа диссоциации фермент-субстратного комплекса
Из уравнения материального баланса имеем: аналитическая концентрация фермента ([Eобщее]) равна сумме концентраций свободного фермента ([E]) и фермент-субстратного комплекса ([ES]): — [Eобщее] = [E] + [ES] 4
Скорость образования продукта реакции Р равна — Vобр продукта = К+2 [ES] 5
Из уравнения (3) имеем: [ES] = [E][S]/Ks, а из уравнения (4) — [E] = [Eобщ ] – [ES], после
подстановки этого значения в предыдущее уравнение получаем:
После преобразования уравнения (6) относительно [ES] имеем:
Подставляя уравнение (7) в уравнение (5) получаем:
Очевидно, что скорость реакции образования продукта будет максимальной при данных условиях когда [ES] = [Eобщ ], т.е. — K+2 [Eобщ] = Vmax
Вводя это значение в уравнение (8) получаем уравнение в виде:
которое называется уравнением Михаэлиса-Ментен, где:
· v – наблюдаемая скорость реакции при данной концентрации субстрата [S];
· KS– константа диссоциации фермент-субстратного комплекса, моль/л;
· Vmax– максимальная скорость реакции при полном насыщении фермента субстратом.
KS и Vmax – это константы, которые не зависят от концентрации субстрата, а характеризуют свойства фермента.
Теоретический график зависимости скорости ферментативной реакции (V) от концентрации субстрата [S] при постоянной концентрации фермента представляет собой график гиперболы.
Из уравнения Михаэлиса–Ментен следует, что при высокой концентрации субстрата и низком значении KS скорость реакции является максимальной, (реакция нулевого порядка – участок (в) на графике). При низкой концентрации субстрата, напротив, скорость реакции оказывается пропорциональной концентрации субстрата в каждый данный момент (реакция первого порядка v = Vmax∙[S] – участок (а) на графике). При средних значениях концентрации субстрата скорость реакции имеет смешанный порядок (участок (Б) на графике) и описывается уравнением Михаэлиса-Ментен.
Следует отметить, что уравнение Михаэлиса–Ментен в его классическом виде было выведено с использованием ряда допущений и, в частности, что образование продукта реакции идет быстро и необратимо. В реальной ферментативной кинетике как раз, как правило, образование продукта реакции процесс обратимый, т.е. более реальная схема ферментативного процесса должна учитывать как минимум 4 константы:
Поэтому были предприняты попытки усовершенствовать уравнение Михаэлиса-Ментен. В том же 1913 году несколько позднее была опубликована работа Бриггса и Холдейна, в которой было предложено уравнение, выведенное в результате анализа рассматриваемой схемы. Однако это уравнение Бриггса-Холдейна:
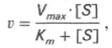
по сути мало отличается от уравнения Михаэлиса-Ментен. Отличие заключается в том, что вместо константы диссоциации фермент-субстратного комплекса Кs = K-1/K+1 в уравнении используется более сложная константа названная позднее константой Михаэлиса Кm. Константа Михаэлиса (Кm) может быть представлена следующим уравнением:
Ферментативная активность. Каталитическая константа — число оборотов фермента. Максимальная скорость ферментативной реакции (Vmax). Константа диссоциации фермент-субстратного комплекса (Ks). Константа Михаэлиса-Ментен (Km).
Особенностью ферментативной кинетики является также то, что экспериментально измеряется не скорость ферментативной реакции, а активность фермента (ферментативная активность). Ранее в лекции №2 уже давалось определение ферментативной активности
Поскольку ферментативная активность не зависит от объема раствора, в котором протекает реакция (она пропорциональна концентрации фермента) ее выражают в специальных единицах: Если размерность скорости реакции – моль/ л·с, то размерность ферментативной активности моль субстрата, превращаемого в единицу времени. Используются следующие единицы активности ферментов:
- Катал. 1 кат = количеству фермента, которое превращает 1 моль субстрата за 1 сек.
- Нкат– нонакатал; 1нкат = 10 9 кат
- Международная единица ферментативой активности (Е) – количество фермента, превращающего 1 мкмоль субстрата в 1 мин.
Удельная активностьвыражается либо 1) количеством единиц (Е или кат, нкат) на 1 мг белка, либо 2) числом молей продукта образовавшегося за 1 минуту на 1 мг белка. Суммарная ферментативная активность определяется как произведение удельной активности на общее количество фермента.
Рассмотрим физический смысл констант уравнения Михаэлиса-Ментен: каталитической константы (К2), максимальной скорости ферментативной реакции (Vmax), константы диссоциации фермент-субстратного комплекса (Ks) и константы Михаэлиса-Ментен (Km).
1. Константа скорости k2 намного выше, чем константа той же, но некаталитической реакции. Константу k2называют каталитической константой скорости ферментативной реакции Ее физический смысл заключается в том, что она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 сек. В связи с этим каталитическая константа еще называется «числом оборотов фермента».
Число оборотов фермента позволяет характеризовать активность ферментов, молекулярная масса которых известна. Чем больше число оборотов фермента, тем он более активен. В настоящее время около 2000 ферментов выделено в чистом виде и молекулярная масса определена у около 150 ферментов. Самым активным ферментом оказалась карбоангидраза, которая катализирует реакцию гидратации углекислого газа. Для нее число оборотов составляет 600.000 сек -1 . Амилаза, которая катализирует гидролиз крахмала, имеет число оборотов 18.300 сек -1 , число оборотов большей части ферментов определяется трех- или четырехзначным числом. Это свидетельствует о высокой активности ферментов. Если фермент не получен в чистом виде, то его активность определяется количеством молей преобразованного субстрата в одну минуту в расчете на 1 мг белка. Эта величина называется удельной активностью фермента. Очевидно, что чем чище ферментный препарат, тем выше окажется его удельная активность.
2. Максимальная скорость реакции (Vmax) как видно из уравнения равна k+2[Eобщ]. Очевидно, что эта величина является константой для данной реакции, проводимой с данной концентрацией фермента, т.е. эта величина также характеризует активность фермента. Если молекулярная масса фермента известна, то экспериментальное значение максимальной скорости реакции при данной молярной концентрации фермента легко может быть пересчитано в число оборотов.
3. Константа диссоциации фермент-субстратного комплекса (Ks)характеризует устойчивость фермент-субстратного комплекса. Чем меньше значение константы тем стабильнее фермент-субстратный комплекс.
4. Константа Михаэлиса (Кm)характеризуетсродствофермента к субстрату. Высокое сродство фермента к субстрату характеризуется низкой величинойКm и наоборот. Величина Кm всегда численно больше чем величинаKs. Константа Михаэлиса численно равна той концентрации субстрата [S], при которой ν достигает половины максимальной величины Vmax (действительно, если v = Vmax/2, то [S] / (Кm + [S]) = 1/2, отсюда Кm = [S]).
Видео:USMLE Step 1 - Фармакология: кинетика ферментов | уравнение Михаелиса - Ментена и не толькоСкачать
Уравнение Михаэлиса-Ментен. Ингибирование ферментов
Страницы работы
Содержание работы
УРАВНЕНИЕ МИХАЭЛИСА —МЕНТЕН
Простейшей моделью для построения и обсуждения теорий ферментативной кинетики является кинетика односубстратных реакций. Хотя чаще всего в реакциях участвует не один, а большее число субстратов, реакцию можно рассматривать как односубстратную, если второй субстрат присутствует в очень большой концентрации. Большинство получаемых выводов можно использовать непосредственно при рассмотрении более сложных ферментативных реакций.
Как уже упоминалось, концентрация субстрата является одним из наиболее важных факторов, определяющих скорость ферментативной реакции.
В начале XX столетия Л. Михаэлисом и М. Ментен было предложено простейшее кинетическое выражение для скорости ферментативной односубстратной реакции.
Схема ферментативного процесса записывается следующим образом:
где Е — фермент; S — субстрат, подвергающийся ферментативной реакции; Р — образующийся в результате продукт;
Уравнение скорости ферментативной реакции, выведенное Михаэлисом и Ментен, предположивших, что превращение субстрата происходит только в переходном фермент-субстратном комплексе, основывается на двух предпосылках.
1. Реакция между ферментом и субстратом находится в равновесии. Это условие выполняется, если скорость распада комплекса на свободный фермент и субстрат значительно больше скорости распада его до свободного фермента и продукта (k-1 >> k2).
2. Концентрация свободного субстрата остается практически постоянной в течение начального периода реакции, тогда концентрация субстрата [S] может быть принята равной полной концентрации субстрата [So]. Это условие выполняется, если полная концентрация субстрата значительно больше полной концентрации фермента, как это обычно имеет место при кинетических исследованиях.
При высокой каталитической активности фермента реальное значение концентрации фермент-субстратного комплекса отличается от его значения в условиях равновесия. Для анализа кинетики реакции с учетом этого обстоятельства Бриггс и Холдейн предложили дополнить теорию Михаэлиса — Ментен условием стационарного состояния.
Согласно этому условию в любой момент реакции скорости образования и распада комплекса ES практически равны, так что концентрация комплекса [ES] может считаться постоянной (квазистационарной) в течение короткого периода времени, необходимого для измерения скорости. В течение более продолжительного периода времени концентрация комплекса [ES] будет изменяться по ходу реакции в связи с падением концентрации субстрата, но скорость изменения ее всегда будет существенно меньше, чем скорость ферментативной реакции.
Для стационарного состояния, при котором
,
k1[E][S] – (k-1 + k2)·[ES] = 0
(1)
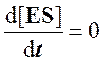
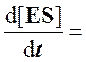
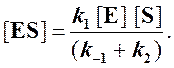
Из уравнения материального баланса для фермента
где [Eo] ─ его начальная концентрация, а [E] ─ текущая концентрация свободного, не связанного в фермент-субстратный комплекс белка, можно записать
и подставить в выражение (1):
Отсюда концентрация ES равна
[ES] = 
Тогда начальная скорость ферментативной реакции, измеряемая по скорости образования продукта Р, равна
(2)
(константа Михаэлиса),
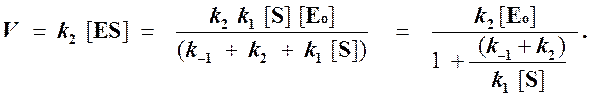
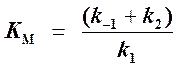
то выражение (2) можно записать в следующем виде:
(3)
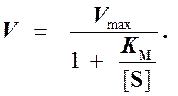
Выражение (3) называется уравнением Михаэлиса —Ментен и описывает зависимость скорости односубстратной ферментативной реакции от концентрации субстрата. Из этого уравнения видно, что при увеличении концентрации субстрата (при неизменной концентрации фермента) скорость реакции стремится к предельному значению, равному Vmax.
При выводе уравнения Михаэлиса — Ментен, кроме вышеперечисленных, принимается во внимание еще несколько не совсем реальных допущений, таких как:
1) отсутствие образования значимого количества комплекса ЕР и других форм фермента;
2) необратимость второй стадии реакции, т. е. образования продукта Р. Это связано с тем, что мы рассматриваем только начальную скорость процесса, когда обратной реакцией из-за фактического отсутствия продукта еще можно пренебречь;
3) связывание с активным центром на каждой субъединице фермента только одной молекулы субстрата;
4) использование для всех реагирующих веществ вместо активностей их концентраций.
Если k2 значительно меньше k-1, то этим членом в выражении константы Михаэлиса можно пренебречь, и КM становится равной отношению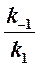 
, а это есть Кd (константа диссоциации фермент-субстратного комплекса):
Таким образом, являясь аналогом константы диссоциации фермент-субстратного комплекса ES, константа Михаэлиса характеризует сродство фермента к субстрату. Чем ниже КM, тем выше сродство.
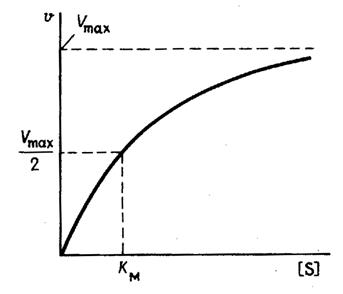
На рис. 1 приведено графическое изображение уравнения Михаэлиса — Ментен.
Рис. 1.Зависимость скорости ферментативной реакции от концентрации субстрата
🌟 Видео
Асеев В. В. - Основы энзимологии - Ферментативная кинетика Уравнение Михаэлиса-МентенСкачать
Разбираем Michaelis-Menten and Lineweaver-Burk plots.Скачать
Асеев В. В. - Основы энзимологии - Кинетика ферментативных реакцийСкачать
ФЕРМЕНТАТИВНАЯ КИНЕТИКА: Занятие 1. Вывод уравнения Михаэлиса-МентенСкачать
Ферментативная кинетикаСкачать
ФЕРМЕНТЫ 5.Основы ферментативного катализа. Кинетика ферментативных реакций.Скачать
Биохимия. Лекция 22. Ферменты. Part 2.Скачать
Лекция 11 || 2021 || Схема Михаэлиса-Ментен (завершение), гетерогенный катализСкачать
Лекция 28.10.20 | Параллельные реакции, катализ, схема Михаэлиса-Ментен | Химическая кинетикаСкачать
Гладилин А.К. - Введение в специальность - 10. Ферментативная кинетикаСкачать
Ферменты ❘ БиохимияСкачать
Лекция 11.11.20 | Схема Михаэлиса-Ментен (завершение), гетерогенный катализ | Химическая кинетикаСкачать
ЛЕКЦИЯ №10 || Химическая кинетика || Лимитирующая стадия (пример), Катализ, схема Михаэлиса – МентенСкачать
Влияние концентрации на скорость химических реакций. 10 класс.Скачать
Ферменты. Эффекторы. Регуляция активности ферментовСкачать
Лекция 10 || 2021 || Параллельные реакции (завершение), катализ, схема Михаэлиса-Ментен (начало)Скачать
Лекция 4 Ферменты Кинетика, ингибирование, изоферментыСкачать
