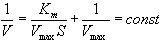Уравнения Михаэлиса-Ментен и Лайнуивера-Берка
Общую теорию ферментативной кинетики и зависимость активности фермента от субстрата.описали Л.Михаэлис и М.Л.Ментен, выразив его в своем уравнении. Бриггс и Холдейн усовершенствовали их уравнение, введя введя в него константу Михаэлиса (Km), определяемую экспериментально.
Уравнение Михаэлиса-Ментен показывает взаимосвязь максимально возможной скорости, реальной скорости реакции, константы Михаэлиса и концентрации субстрата. Так как пользоваться графиком, построенным в прямых координатах V и [S] для точных расчетов неудобно, то Г.Лайнуивер и Д.Бэрк преобразовали уравнение Бриггса–Холдейна в обратные координаты.
Уравнение Михаэлиса-Ментен
Уравнение Лайнуивера-Бэрка
На самом деле уравнение Михаэлиса-Ментен в данном виде предложили Бриггс и Холдейн, но в честь основоположников оно носит название Михаэлиса-Ментен.
Выделяют три основных решения уравнения Михаэлиса-Ментен:
1. Концентрация субстрата равна величине константы Михаэлиса ([S] = Km).
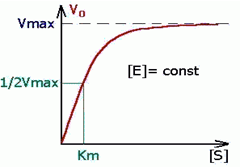
В этом случае, решая уравнение Михаэлиса-Ментен, получаем, что скорость реакции V будет равна половине максимальной Vmax.(V = ½ Vmax).
В математическом смысле Km соответствует концентрации субстрата при которой скорость реакции равна половине максимальной. Ее биологический смысл заключается в характеристике сродства фермента к субстрату, а именно: увеличение величины Кm означает снижение сродства фермента к субстрату.
2. Концентрация субстрата значительно больше Km ([S] >> Km). В этом случае величиной Km можно пренебречь, при решении получим, что скорость реакции максимальна (плато на графике).
3. Концентрация субстрата значительно меньше Km ([S]
Видео:Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать

Анализ уравнения Михаэлиса-Ментена
1. Если концентрация субстрата в реакции низкая, т. е. [S] > Кs, величиной К можно пренебречь, тогда
где Vбиохим.р. = Vmax – уравнение нулевого порядка.
Уравнение Михаэлиса-Ментена было преобразовано Лайнуивером и Берком по методу двойных обратных величин: если имеется равенство между двумя величинами, то и обратные величины тоже равны:
1/V = (1/V) / (KS + [S]) / [S] – уравнение Михаэлиса — Ментена.

Уравнение Михаэлиса-Ментена, где КS = К-1/K+1, носит ограниченный характер, так как учитывает только первый период процесса
и не учитывает второй
Оно справедливо лишь для коротких сроков действия ферментов, когда наблюдается избыток субстрата и малый выход продукта реакции.
Д. Холдейн и Д. Бриггс для механизма Е + S ↔ ЕS ↔ Е + Р
вывели улучшенное уравнение Михаэлиса- Ментена:

где Кm = К-1 + К+2 / К+1 – константа Михаэлиса.
Константа Михаэлиса Кm является важной характеристикой фермента, которая определяет его сродство к субстрату:
Так как Кs = К-1 / К+1, то Кm > Кs, на величину К+2 / К+1. Константу Михаэлиса выражают в молях на литр (моль/л).
Физический смысл константы Михаэлиса
Если V = 1/2V, то Кm = [S]. Константа Михаэлиса равна концентрации субстрата (S), при которой наблюдается скорость реакции, равная 1/2 максимальной скорости (моль/л).
5.4. Методы графического определения константы Михаэлиса
Графическое изображение константы Михаэлиса выглядит следующим образом:
На графике по оси абсцисс откладывают концентрацию субстрата, по оси ординат – скорость реакции V, причем V – максимальная скорость, а V/2 – половина максимальной скорости. Отрезок на оси абсцисс – Кm.
Кроме того, используется графический способ определения константы Михаэлиса по методу двойных обратных величин Лайнуивера и Берка.
Уравнение Лайнуивера – Берка имеет вид:
Это уравнение изображено на графике прямой линией у = ах + b. По оси абсцисс откладывают 1/[S], по оси ординат – 1/V. Наклон полученной прямой равен Кm/V, отрезок, отсекаемый прямой от оси ординат – 1/V.Если полученную прямую продолжить за ось ординат, то она отсечет от оси абсцисс отрезок, равный обратной величине константы Михаэлиса – 1/Кm.
Определить значение константы Михаэлиса можно также по графику Иди-Хофсти:
Количественная характеристика активности фермента
В настоящее время используют две единицы ферментативной активности: стандартная единица U (или единица активности) и катал.
Единица активности U фермента – это такое его количество, которое при определенных условиях катализирует превращение 1 мкмоль субстрата в 1 мин, или, если атаке подвергается более чем одна связь в молекуле субстрата, 1 мк-экв (группы) в 1 мин.
Катал (кат) – это каталитическая активность фермента, которая увеличивает скорость реакции на 1 моль/с в определенной тест-системе.
В обоих случаях строго оговариваются условия, т. е. температура, рН, концентрация субстрата.
Удельную активность фермента определяют путем деления числа единиц ферментативной активности на массу белка или ткани (в г или мг).
Молярную активность фермента определяют путем деления числа единиц ферментативной активности в образце на массу фермента, выраженную в микромолях (для очищенных ферментов):

Видео:USMLE Step 1 - Фармакология: кинетика ферментов | уравнение Михаелиса - Ментена и не толькоСкачать

Это и есть уравнение Михаэлиса-Ментен.
Вариант 3.
Уравнение Михаэлиса – Ментена, его вывод и анализ приложенности к описанию зависимости начальной скорости ферментативных реакций от концентрации субстрата.
ВЫВОД И АНАЛИЗ УР МИХАЭЛИСА-МЕНТЕН
Михаэлис и Ментен предположили, что мех-м ферм р-й описывается моделью:
При формулировке кинетического выражения для скорости ферментативной реакции Михаэлис и Ментен сделали три допущения:
1) Стационарное состояние реакции в момент равновесия, когда скорости образования и расходования ES равны;
2) Весь фермент в условиях насыщающих концентраций субстрата превращается в энзимсубстратный комплекс ES;
3) Если весь фермент в виде ES, то скорость реакции максимальна и Vmax=k2[ES].
Образование ES: [ES]=k1[S][E] (I)
Расходование ES: [ES]=k-1[ES]+k2[ES] (II)
Приравнивая выражения (I) и (II) и сокращая обе части на k1 получаем:
[S][E] = [ES](k-1 + k2)/k1 = [ES]Km, где Km = (k-1 + k2)/k1
Выразим равновесную концентрацию [E] через начальную [Eo]: [E] = [Eo] — [ES]
[S]([Eo]-[ES])= [ES]Km, переносим [S] в правую часть выражения и делим обе части на [ES]:
Поскольку трудно (если не невозможно) измерить [ES], произведем замену с учетом того, что в насыщающих концентрациях [S] весь [Eo] перейдет в [ES] и максимальная скорость при этом будет равна Vmax=k2[ES]=k2[Eo].
В это же время скорость реакции равна V=k2[ES]. Через отношение этих скоростей выразим [Eo]/[ES]:
В уравнении (III) произведем замену отношения [Eo]/[ES] на Vmax/V и получаем:
Это и есть уравнение Михаэлиса-Ментен.
Ограничения кинетики Михаэлиса-Ментен
Михаэлис и Ментен вывели уравнение с учетом двух предположений (быстро устанавливающееся равновесие и избыток субстрата). Позднее было показано, что уравнение справедливо, то есть хорошо описывает реакцию, при выполнении всех следующих условий.
7 основных постулатов для выполнения уравнения Михаэлиса-Ментен.
1. В ходе реакции образуется кинетически устойчивый фермент-субстратный комплекс.
2. Определяемая с помощью уравнения константа Кs является константой диссоциации фермент-субстратного комплекса: это справедливо, только если k2
V = Vmax[S]/(Km+[S]) — ур михаэлиса-ментен
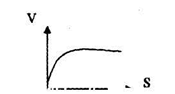
Граф зав-сть для ур имеет вид: Кривая уравнения Михаэли-са-Ментен: гиперболическая зависимость начальных скоростей катализируемой ферментом реакции от концентрации субстрата.
Константа Михаэлиса измеряется в молях на литр и бывает от 10-2 до 10-7, чем меньше Кm, тем активнее фермент. При V=1/2Vmax, имеем Km = [S]. Однако, определение Vmax затруднительно по асимптоте. Для устранения этого неудобства ЛАЙНУИВЕР и БЭРК приравняли обратные зависимости левой и правой частей уравнения.
Своеобразие проявления второго закона термодинамики в биологических системах.
— ограничивает переход какой –либо Е в работу или в другой тип энергии. Ни какой тип Е не может перейти в работу с КПД – 100%.
1) не возможно перевести тепло от более холодной системы к более горячей без соответствующих изменений в этих системах и в окр. среде, т.е нельзя закипятить стакан с водой в холодильнике.
2) Самопроизвольно могут протекать лишь те процессы, которые связаны с переносом Е от более высокого уровня к более низкому, т.е. по градиенту.
3) Невозможно совершить работу против градиента без соответствующих изменений.
Градиент — векторная величина, разность величин того или иного параметра в 2-х точках, отнесенных к расстоянию между ними. Градиент концентрации – это концентрация «в» и «извне» на толщину мембраны (осмотич. градиент, концентрационный гр. (транспорт ионов и др. в-в), электрический гр.).
Все процессы, протекающее в природе, подчиняются первому закону ТД, однако не всякий возможный процесс осуществим на практике. Исходя из первого закона, нельзя определить направление самопроизвольного процесса. Второй закон ТД позволяет предсказать направление пр-са при заданных усл.. В отл. от 1 закона ТД он не носит всеобщего характера и применим лишь к сист., сост. из большого числа частиц.
14. Доказательства применимости второго закона ТД к биосистемам.
Применимость второго закона ТД к биосистемам:
1. Второй закон ТД был сформулирован для характристики изолированных систем. Реальные био системы являются открытыми.
2. Значение энтропии строго определено для равновесного состояния. Био системы в своем развитии проходят через целый ряд неравновесных состояний.
Развитие орг-мов сопровождаются усложнением их организации – это самопроизвольное ↓ энтропии живых систем. В реальных усл. развитие орг-мов, сопр-ся ↓ общей величины их энтропии за счет того, что в др. участках внешней среды идут сопряженные процессы с обр-нием положительной энтропии. Суммарное изменение энтропии в системе организм + внешняя среда всегда положительно.
Био системы характеризуются наличием большого кол-ва градиентов (осмотический, электрический, концентрационный). Градиент какого-либо т/д параметра изменяется с расстоянием. Биосистема способна совершать работу, если в ней имеется градиент. Градиент – своеобразное депо энергии.
Совершение работы в системе связано с реализацией этой свободной энергии. Если совершается работа, то градиент, за счет Е которого это происходит, ↓, но параллельно возникает другой градиент противоположной направленности. При необратимых пр-сах величина второго градиента будет меньше, чем величина первого.
Вариант 1.
Закон термодинамики, закон Гисса, термодинамическое равновесие, стационарные системы.
8. Первый закон ТД в биологии; доказательства его применимости к живым системам. Своеобразие проявления первого закона ТД в биосистемах.
Закон: работа совершаемая системой = разности м/у количеством теплоты, сообщаемой системой и изменением её внутр. Е: ∆А = ∆Q — ∆U. Закон – это количественная форма закона сохранения энергии. Кол-во теплоты, поступающей в систему расходуется на ↑ внутр. Е системы за вычетом совершенной работы.
Внутренняя Е (U) – сумма (совокупность) всех типов Е и взаимодействий входящих в систему частиц. (Е вращательного движения атомов, Е взаим-вия водородных атомов).
Работа биоситемы может совершаться за счёт энтропии и внутр. Е (но не внеш. теплоты, т.к. если бы можно было за счёт притока из вне биосист. нагревались бы 1740С, см. ниже в этом же вопросе – это типа своеобразие закона) (это следствие 1 закона).
Доказательство справедливости закона для био систем: 1780 Лавуазье и Лаплас опыт с морскими свинками. Е хим. связей в белках, жирах и углеводах переходит в тепловую – метод непрямой (?) калориметрии. Свинок кормили – мерили тепло, столько же хавчика сжигали – тоже мерили, сравнили, получили числа одного порядка. По умному: совпадение тепловых эффектов при прямом сжигании продуктов и при их окислении в орг-ме морской свинки свид-т о том, что пути превращения прод-в питания в метаб-ких процессах и хим. р-циях вне живой клетки яв-ся эквивалент-ми с точки зрения суммарных тепловых эффектов. Живые орг-мы не являются источником новой Е. Окисление поступающих в живой организм пит. в-в приводит к высвобождению в нем эквивалетного к-ва Е.
Еще док-во: работа мышцы при 250С (289К = Т), КПД = 30% = 1/3.
Т1 = (298*3) /2 = 447К = 1740С.
Метод прямой калориметрии исполь-ся и на человеке (Этуотер). Исполь-ся герметичная камера: ч/з систему труб подается определ. кол-во О2, считают сколько выд-ся СО2, Н2О и т.д. есть датчики на t. Ограничения: 1) живой объект не должен накапливать массу и расти. 2) жив организм не должен совершать работу (физ. нагрузку). Кол-во Е, поглощенной за сутки чел. орг-мом вместе с пит. в-ми, равно выделенной за это же время теплоте. След-но, закон справедлив для жив. орг-мов.
Метод непрямой калориметрии: С полным и неполным газовым анализом. Ввели коэффициент: при расщеплении 1 мол-лы глюкозы исп-ся 6 мол-л О2, а выделяется 6 мол-л СО2, 6 мол-л Н2О и 678 кал. ДК = выд СО2 в ед времени / погл О2 в ед времени. Производят сравнение состава и объема вдых. и выдых. воздуха. Исп. мешок Дугласа. Для анализа исп. газоанализаторы: ГА Холдейна: система стеклян. трубочек, погл-щая CO2 и O2. Сейчас ГА с поглощением световых потоков. Нормальный дых. коэфф. 0,85±0,03. Нахождение КЭК (калориметрический эквивалент кислорода) – численно равен кол-ву Е, высвобождающейся в организме при потреблении 1 л О2. В клинических условиях исп. неполный ГА, не считают СО2. Считают объем поглощенного О2 с пом. спирографа. Диаграмма под наклоном, из замкнутой системы постепенно уходит О2.
10. Закон Гесса, его применимость к биопроцессам.Следствие закона Гесса, его практическое значение.
Теплоту у теплокровных раздел. на 2 типа:1) первичная (осн. обмен, Q, кот. выд-ся сразу после поглощения пищи при взаимод. с О2, т.е выд-ся в рез-те протекания биохим. проц-ов. В живых орг-мах любая хим. р-ция идет с КПД термин «тепловой эффект р-ции» заменяют термином «энтальпия р-ции». Энтальпия р-ции – это изменение энтальпии системы при протекании химической реакции. Она может быть больше нуля или меньше нуля. Если ∆H > 0, то Q > 0 (эндотермические реакции).
Для равновесного сост. S стремится к мах, U=0. Стац. сост. отличается тем, что S ≠ мах, а является постоянной величиной, S=const, U не равняется 0, U=const. Ежесекундный прирост энтропии стремится к min. Любая живая система может находиться только в стац. сост. Если достигнуто состояние ТД равновесия — это уже не живая система. Качество стационарного состояния может быть различным.
В открытых системах:
S состоит из двух показателей.
Si – внутри самой сист., S — самой системы, Se – внешняя среда.
dS=dSi+dSe (d – это ∆ — это изменение)
Когда dSe > dSi и dSe 0.
Состоянию ТД равновесия — характерно мах значение S (S=max), U=0, т.е. Е, которая расходуется на совершение А.
Сходство: стац. и равновесное состояния не зависят от времени.
Отличия стац. сост. от равновесия (из конспекта):
1) своб. Е (∆G) в стац. сост. есть величина постоянная во времени и не равна 0. В ТД равн. ∆G=const, но ∆G =0 => открытые сист., если вывести из стац. сост. могут совершать работу; при ТД равновесии не способны совершать работу.
2) энтропия. В стац. сост. =const, но она не max. (∆G) ∆S ≠ max = const.
3) . в стац. сост. проявляется кинетический параметр (фактор) (изменение энтропии во времени) dS/dt = dSi/dt + dSe/dt.
* постоянный обмен энергией с окружающей средой
* постоянно тратится свободная энергия на поддержание состояния
* т/д потенциалы постоянны, G и F не равны 0
* энтропия постоянна, но не максимальна
* отсутствует поток вещества и энергии в окружающую среду и обратно
* на поддержание этого состояния не затрачивается свободная энергия
* работа способности системы равна 0, т/д потенциалы равны 0
* в системе отсутствуют градиенты
Переход на новый стац. уровень:
2 пути: 1) «овершот» — по нему переходят живые организмы при изм внеш. усл. (приспособление). График.
Нижняя стрелочка – это старый стац. уровень.
Верхняя стрелочка – это новый стац. уровень.
2) «ложный старт» — усиление или уменьшение О2, выращивание лука с О2 и без. График. С О2 – аэробный распад углеродов. Без О2 – обмен в-в переходит на анаэробный путь. А если потом снова дать О2 – то получится график 2 (то что обведено кружочком – там осущ-ся уничтожение продуктов анаэробного пути). Пример для чела: пока не расщепится молочная к-та осуществлять работу дальше нельзя.
17. Теорема Пригожина и направленность эволюции биосистем. Энтропия и биологический прогресс.
Стац. сост. хар-ся min ежесекундным приростом энтропии (благодаря этому происходит эволюция).
Теорема: при постоянных внеш. усл. в системе, находящейся вблизи положения ТД равновесия в стац. сост., скорость возрастания энтропии, за счёт необходимости внутр. процессов, принимает постоянное минимальное значение отличное от нуля.
Или: В стационарных состояниях при фиксированных внешних параметрах локальная продукция энтропии в открытой т/д системе стремится к минимальному значению.
Энтропия – мера рассеивания свободной энергии, следовательно любая открытая т/д система в стационарном состоянии стремится к минимальному рассеиванию свободной энергии. Если в силу причин система отклонилась от стационарного состояния, то вследствие стремления системы к минимальной энтропии, в ней возникают внутренние изменения, возвращающие ее в стационарное состояние.
Величина, кот это всё характеризует:
β= T* (dS/dt), где β – диссипативная фукнкция. β>0, min. С этим связан Критерий эволюции открытых систем: ∆β/dt происходит преобразование одного вида Е в другой – это центральное событие фотосинтеза.
Физ-хим. сущность фотосинтеза: Ф. – процесс преобразования электромагнитной Е в Е хим. связей, сопровождающийся ↑ энергетического потенциала системы. Система является ТД открытой. При поглощении солнечного излучения растениями, водорослями, нек. микро, возрастают уровни свободной Е (∆F) и общей энергии (∆U), в которой значительную часть составляет Е электрона: ∆F = ∆U — Т∆S
КПД процесса фотосинтеза составляет обычно 6-8%, у хлореллы он достигает 20-25%. Большая часть поглощённой листом энергии теряется на тепловое излучение. В энергию химич. связей включается в ср. 1—2% поглощённой ФАР. Осн. показатель Ф.— его интенсивность, т. е. кол-во газа, поглощённого или выделенного единицей массы или поверхности листа в единицу времени. Интенсивность Ф. зависит от вида растений, состояния листьев, внеш. условий (свет, СO2). Ф. лесных древесных растений в 5—8 раз ниже, чем Ф. травянистых растений открытых местообитаний.
Реакции, протекающие под воздействием светового излучения, называются фотохимическими Основной закон фотохимии – закон квантовой эквивалентности (А. Эйнштейн, 1912 г): каждый поглощенный квант света hν вызывает изменение одной молекулы.
Важнейшим параметром фотохимической реакции служит квантовый выход γ:
γ = число фотохим. превращений/число поглощений квантов.
В зависимости от типа фотохимической реакции квантовый выход может меняться в широких пределах. Это связано с возможностью потери поглощенной энергии до фотопревращения. Если время существования фотовозбужденной молекулы и скорость фотодиссоциации совпадают, то γ
1. При γ >> 1 фотореакция идет по цепному механизму. В частности для реакции H2 + Cl2 = 2HCl γ = 105.
Типы фотохимических реакций:
1) Фотодиссоциация (фотолиз) приводит к разложению исходного вещества, поглотившего световую энергию. Примерами реакции фоторазложения служат такие: разложение галогенидов серебра (основа серебряной фотографии), фотолиз паров ацетона CH3CO CH3 → CO + другие продукты.
2) Фотосинтез приводит к образованию более сложных соединений. Примерами реакций фотосинтеза служат:
фотосинтез озона в верхних слоях атмосферы, создающий защитный озоновый слой:
О2→О +О — фотодиссоциация
О2+ О→ О3 — фотосинтез
фотосинтез органических соединений из углекислого газа, воды, минеральных веществ зелеными растениями. В частности, синтез глюкозы может быть описан уравнением:
6СО2 + 6Н2О →глюкоза + 6О2
3) Фотохромизм – явление обратимого изменения пространственного или электронного строения молекул под действием света, сопровождающееся изменением окраски вещества. На основе фотохромных материалов изготовляются линзы с переменным светопропусканием, оконные стекла, фотохромные системы на основе некоторых органических и координационных соединений.
Вариант 2.
Графическая зависимость скорости реакции от субстрата, фермента и температуры
42 Зависимость скор р-ции от темп. Ур Аррениуса
Для характеристики зависимости скорости химической реакции от температуры было введено понятие температурного коэффициента скорости (γ), равного отношению константы скорости при температуре (Т + 10) к константе скорости при температуре Т (т.е. γ показывает, во сколько раз изменяется константа скорости при увеличении температуры на 10 градусов):
Температурный коэф. Вант-гоффа-Q10= V t+10/V t.
Экспериментально было установлено, что повышение температуры на 10 К в области обычных температур (≈ 300 К) увеличивает скорость многих гомогенных реакций в 2 4 раза, т. е. для этих реакций γ = (2 4). Это правило называется правилом Вант–Гоффа.
В общем случае отношение констант скорости реакции k2 и k1, определенных при двух различных температурах Т2 и Т1, равно
Более точную зависимость скорости реакции от температуры дает уравнение Аррениуса:
где k — константа скорости реакции, R — универсальная газовая постоянная, Е — энергия активации химической реакции. В случае простых реакций величина Е показывает, какой минимальной (избыточной по сравнению со средней) энергией в расчете на 1 моль должны обладать реагирующие частицы, чтобы они могли вступить в химическую реакцию. В случае сложных реакций величина Е называется эмпирической или кажущейся энергией активации и в общем случае зависит от энергий активации отдельных стадий данной реакции.
Проинтегрировав уравнение (10.16), получим уравнение Аррениуса в интегральной форме:
где А — предэкспоненциальный множитель. Физический смысл А в случае простых реакций: мономолекулярных — это частота колебаний по разрываемой связи (А 1013 сек-1), бимолекулярных — величина А пропорциональна общему числу столкновений между молекулами реагирующих веществ (А 10-10 10-11 см3/(мол-л•сек).
Есть еще такое Ур-е: V= pZeEакт/RT, где р-стерический фактор, Z- число столкновений молекул, Еакт — энергия активации
Зависимость скорости реакции от температуры дает уравнение Аррениуса:
где k — константа скорости реакции, R — универсальная газовая постоянная, Е — энергия активации химической реакции. В случае простых реакций величина Е показывает, какой минимальной (избыточной по сравнению со средней) энергией в расчете на 1 моль должны обладать реагирующие частицы, чтобы они могли вступить в химическую реакцию. В случае сложных реакций величина Е называется эмпирической или кажущейся энергией активации и в общем случае зависит от энергий активации отдельных стадий данной реакции.
Проинтегрировав уравнение (10.16), получим уравнение Аррениуса в интегральной форме:
где А — предэкспоненциальный множитель. Физический смысл А в случае простых реакций: мономолекулярных — это частота колебаний по разрываемой связи (А 1013 сек-1), бимолекулярных — величина А пропорциональна общему числу столкновений между молекулами реагирующих веществ (А 10-10 10-11 см3/(мол-л•сек).
Проинтегрировав ур-е (10.16) в пределах температур от Т1 до Т2, получим:
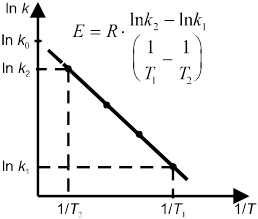
Энергию активации можно определить как аналитически по уравнению (10.18), так и графическим методом. Для этого необходимо знать ряд констант скоростей при разных температурах. Если реакция подчиняется уравнению Аррениуса, то зависимость lnk от 1/T должна выражаться прямой линией, что следует из уравнения (10.17) (рис. 7).
Для очень большого числа реакций энергия активации находится в пределах от 60 до 240 кДж/моль, т.е. примерно соответствует энергиям химических связей.
Энерг актив. Связана с Q10: Е=0,46T1*T2lgQ10
44 КИНЕТИКА ФЕРМЕНТ РЕАКЦИЙ, акт ферм, ед измерен акт и колич ферм.
ферм– это специфические органические катализаторы, синтезируемые живыми клетками. Как правило все ферменты представляют собой белки с различными молекулярными массами: от 9 кДа до 1000 кДа. Каждый фермент катализирует определённую химическую реакцию.
Субст- это вещества, с которыми происходит химическое превращение под действием ферментов. Субстратами ферментов могут быть как природные, так и химически синтезированные вещества.
1. с 1 активным центром (связывает S, расщепляет связи + связан с активацией и
2. кроме активного каталитического центра имеется аллостерический центр.
По взаимодействию с кофакторами:
1. ковалентная связь с кофактором — простетическая группа
2. нековалентное связывание — отделяется при гидролизе.
1. ускоряют протекание реакций
2. являются специфичными (мало-, относительно, абсолютно)
При присоединении субстрата к ферменту, его связи переходят в напряжённое состояние, что снижает энергию активации.
Факторы влияющие на активность:
t — идет как ферментативный процесс, так и денатурация белка. Q10 – 2
2. кислотность среды. Амилаза слюны — рН =7-7.5 , пепсин желудка
3. концентрация S
На начальном участке графика [S] низкая→ реакция первого порядка.
На втором — переходная стадия → переходный порядок реакции. На третьем участке (плато) → перенасыщение S→0 порядок реакции.
Кат. акт ферм — это способность фермента превращать большое количество молекул субстрата, в то время как сам он к концу реакции остается неизменным. Ферменты различаются по своей каталитической способности. Например, 1 моль трипсина осуществляет 102 циклов в секунду, глюкозоксидаза — 17×103 циклов в секунду и т.д. Это называется “числом оборотов фермента”. Число оборотов варьирует от 1 до 106 в зависимости от природы фермента. Каталитическую активность ферментов выражают в единицах активности.
Международная ед акт (E) — это количество фермента, которое катализирует превращение 1 мкмоля субстрата в 1 минуту в оптимальных условиях.
Ед акт в системе СИ (катал) — соответствует количеству фермента, которое катализирует превращение 1 моля субстрата в 1 секунду.
Соотношение между единицами активности: 1 E = 16,67 нанокатал; В медицине активность ферментов выражают чаще всего в единицах активности на 1 л биологической жидкости. Удельная активность фермента — это активность, выраженная в единицах активности на 1 мг (или 1 г) белка или 1 мг (1 г) препарата фермента. Используется в биохимической практике.
45 Осн положен теор ферм кинетики и общ теор действ фер-та
Предварительные эксперименты по изучению кинетики ферментативных реакций показали, что скорость реакции E + S —> E + P, вопреки теоретическим ожиданиям, не зависит от концентрации фермента и субстрата так, как в случае обычной реакции второго порядка. Самая ранняя попытка математически описать ферментативные реакции была предпринята Дюкло в 1898 г. Браун (1902) и независимо от него Анри (1903) впервые выдвинули гипотезу об образовании в ходе реакции фермент-субстратного комплекса. Это предположение основывалось на трех экспериментальных фактах:
1. папаин образовывал нерастворимое соединение с фибрином
2. субстрат инвертазы — сахароза могла защищать фермент от тепловой денатурации
3. было показано, что ферменты являются стереохимически специфическими катализаторами
Х-КА ДЕЙСТВИЯ ФЕРМ:
1. специфичность действия-способность ускорять протекание 1 или нескольких реакций (амилазная реакция расщепляет крахмал до глюкозы)
а. абсолютная- определенный субстрат;
б. относительная- ферменты, которые катализируют ращепление определенного типа связи. (пепсин)
2. ускорение протекания ферментативн. Реакций- каталитичность. Ферменты действуют в мыгких условиях (норм давление, pH, температура): гидролиз крахмала
Амилаза = 37 градусов, pH7, скорость выше, чем при неорган.катализе.
2. регулируемость – есть факторы под воздействием которых скорость может увеличится или уменшаться
В 1913 году Михаэлис и Ментен опубликовали свою теорию общего механизма ферментативных реакций. Их уравнение стало фундаментальным принципом всех кинетических исследований ферментов вот уже почти целый век.
т.е. фермент Е вступает во взаимодействие с субстратом S с образованием промежуточного комплекса ES, который далее распадается на свободный фермент и продукт реакции Р. Математическая обработка на основе закона действующих масс дала возможность вывести уравнение, названное в честь авторов уравнением Михаэлиса–Ментен, выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:
где v – наблюдаемая скорость реакции при данной концентрации субстрата [S]; KS– константа диссоциации фермент-субстратного комплекса, моль/л; Vmax– максимальная скорость реакции при полном насыщении фермента субстратом.
Основной механизм действия ферментов-они снижают Е активации за счет образования фермент-субстрат копмлекса.
Катализ приводит к ускорению достижения равновесия за счет снижения энергии активации (Еа), часто ступенчато.
Три стадии процесса:
1) E + S —— ES (K = k1/k-1) (БЫСТРАЯ)
2) ES —— EP (k2)(медленная)
Таким образом, в момент равновесия скорости образования и исчезновения энзимсубстратного комплекса (ES) равны:
🔥 Видео
ФЕРМЕНТАТИВНАЯ КИНЕТИКА: Занятие 1. Вывод уравнения Михаэлиса-МентенСкачать

Разбираем Michaelis-Menten and Lineweaver-Burk plots.Скачать
Асеев В. В. - Основы энзимологии - Ферментативная кинетика Уравнение Михаэлиса-МентенСкачать
Асеев В. В. - Основы энзимологии - Кинетика ферментативных реакцийСкачать

Ферментативная кинетикаСкачать

Кинетика. О чем говорят графики. БиохимияСкачать

Рубин А. Б. - Биофизика I - Ферментативные реакцииСкачать

Гладилин А.К. - Введение в специальность - 10. Ферментативная кинетикаСкачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать

ФЕРМЕНТЫ 5.Основы ферментативного катализа. Кинетика ферментативных реакций.Скачать

Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Гладилин А.К. - Введение в специальность - 12. Полное неконкурентное ингибированиеСкачать

25. Схема реакции и химическое уравнениеСкачать

Лекция 11 || 2021 || Схема Михаэлиса-Ментен (завершение), гетерогенный катализСкачать

Химическое равновесие. Закон действующих масс.Скачать

Лекция 10 || 2021 || Параллельные реакции (завершение), катализ, схема Михаэлиса-Ментен (начало)Скачать

Уравнение Гендерсона-ХассельбахаСкачать

Этапы ферментативного катализа. Взаимодействие ферментов с несколькими субстратамиСкачать