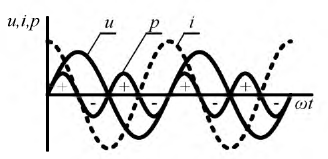
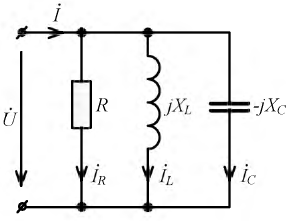
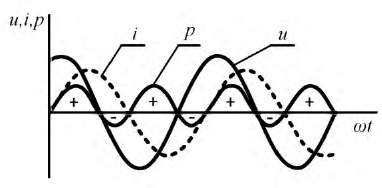
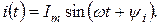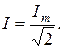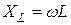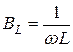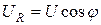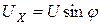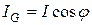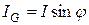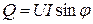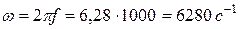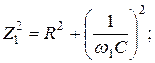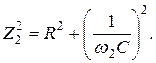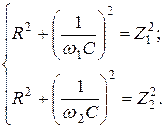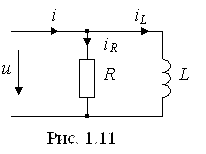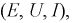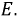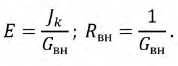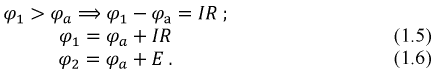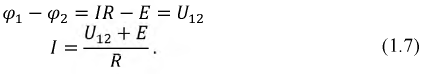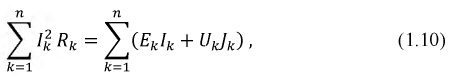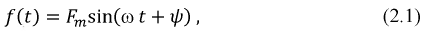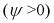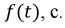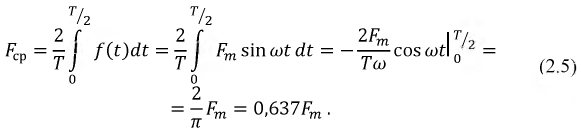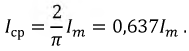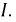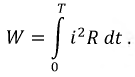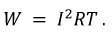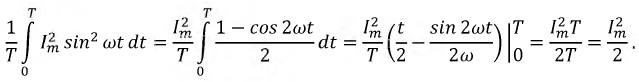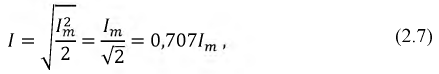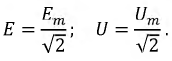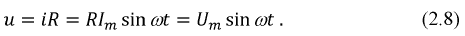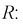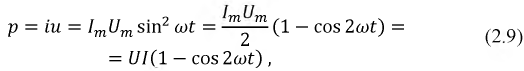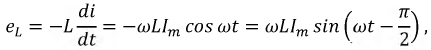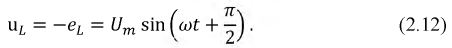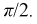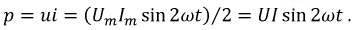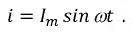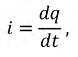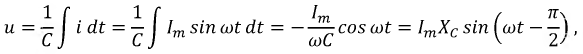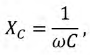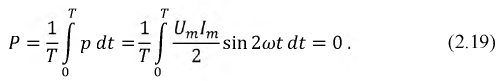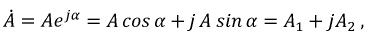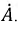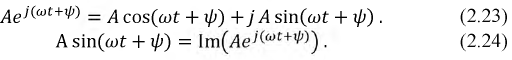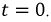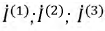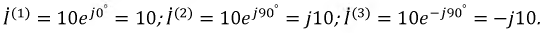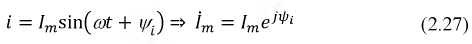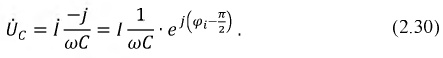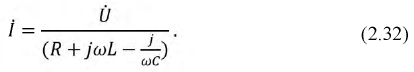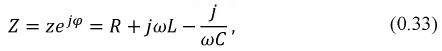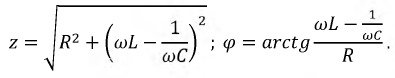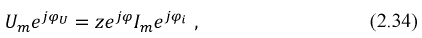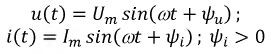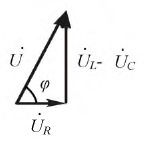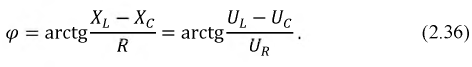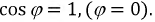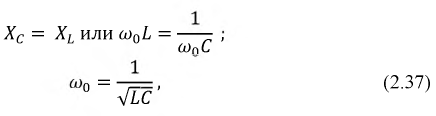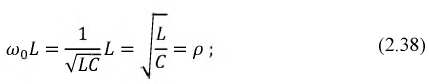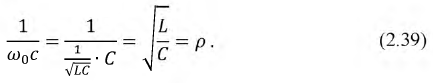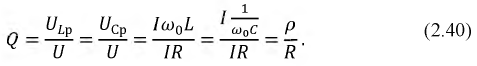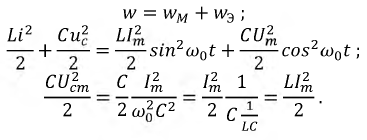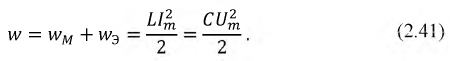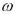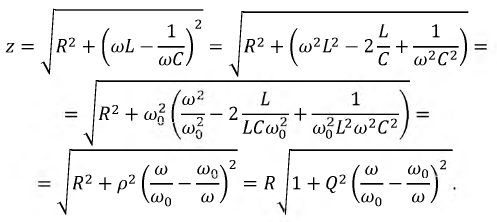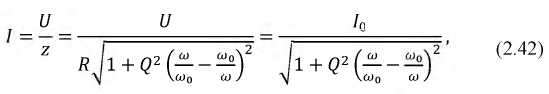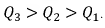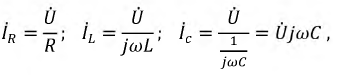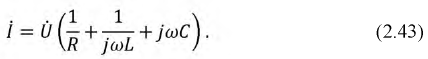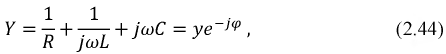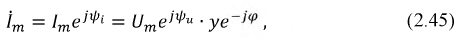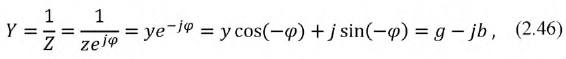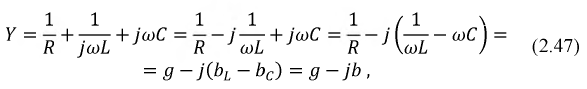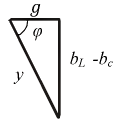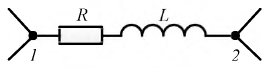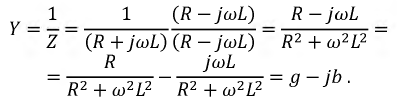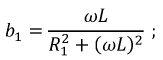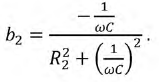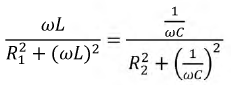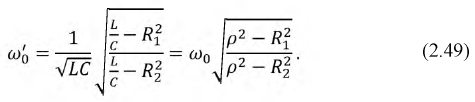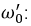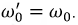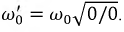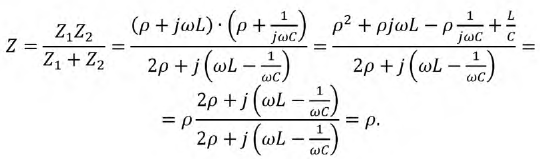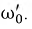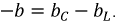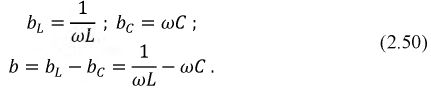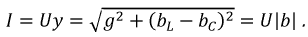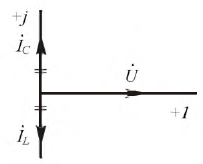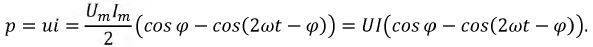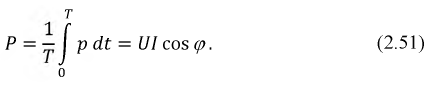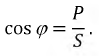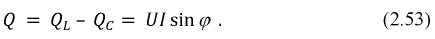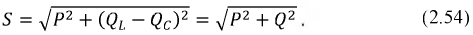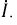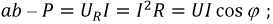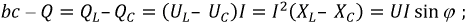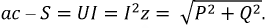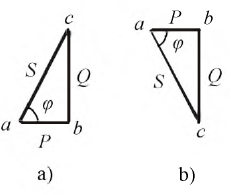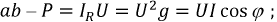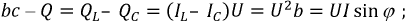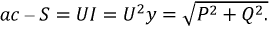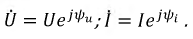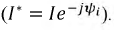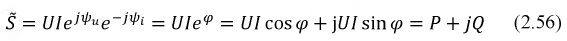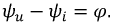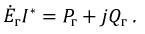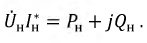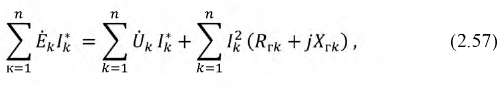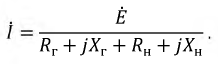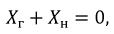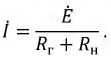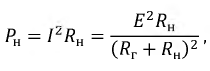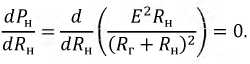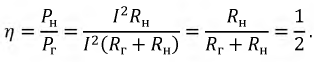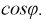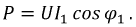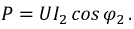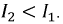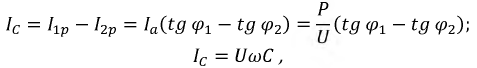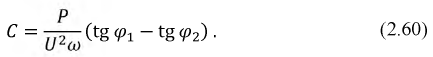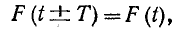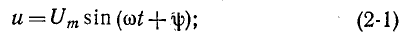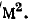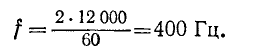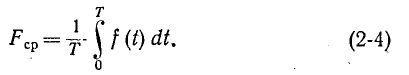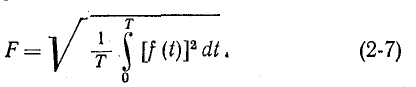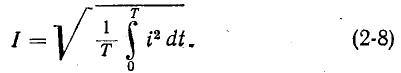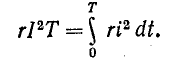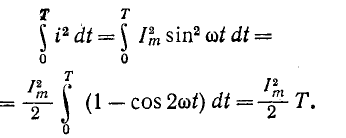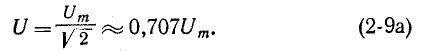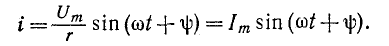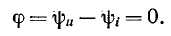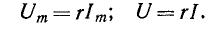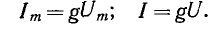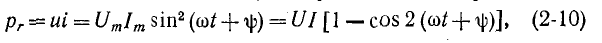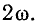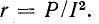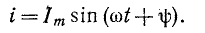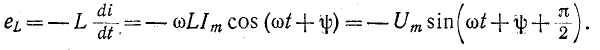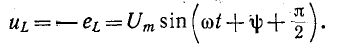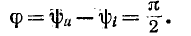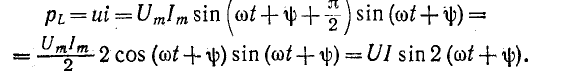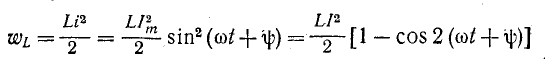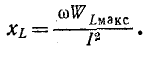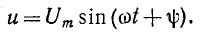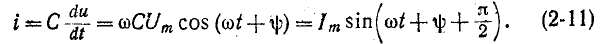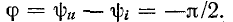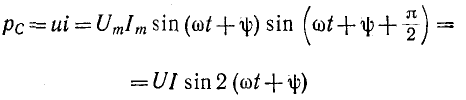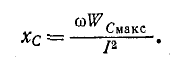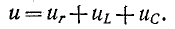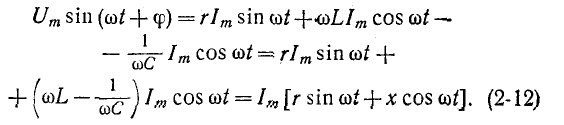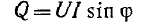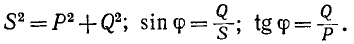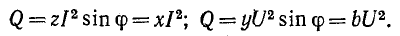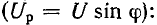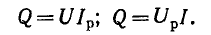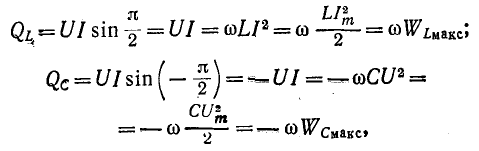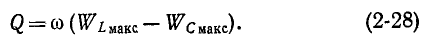Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC — Direct Current — постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
- Параметры переменного тока и напряжения
- Коэффициент амплитуды и коэффициент формы
- Решение типовых задач. Синусоидальные токи, напряжения
- Однофазные цепи синусоидального тока
- Закон Ома
- Законы Кирхгофа
- Цепи однофазного синусоидального тока и напряжения
- Среднее и действующее значения периодической функции (тока и напряжения)
- Элементы R, L, C в цепях синусоидального тока
- Синусоидальный ток в индуктивном элементе
- Синусоидальный ток в емкостном элементе
- Изображение синусоидальных функций времени (напряжение, сила тока) векторами на комплексной плоскости
- Основы символического (комплексного) метода расчета цепей синусоидального тока
- Последовательное соединение элементов R L C
- Резонанс напряжений
- Частотные характеристики последовательного колебательного контура
- Параллельное соединение элементов R L C
- Резонанс токов
- Частотные характеристики параллельного колебательного контура
- Мощность в цепи синусоидального тока
- Выражение мощности в комплексной форме
- Передача энергии от активного двухполюсника к пассивному
- Коэффициент мощности
- Электрическая цепь однофазного синусоидального тока
- Генерирование синусоидальной э. д. с.
- Среднее и действующее значения функции
- Синусоидальный ток в сопротивлении
- Синусоидальный ток в индуктивности
- Синусоидальный ток в емкости
- Последовательное соединение
- 💥 Видео
Видео:Амплитуда, период, частота и мгновенное значение переменного токаСкачать

Параметры переменного тока и напряжения

Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f — величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz). Частота f = 1 /T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
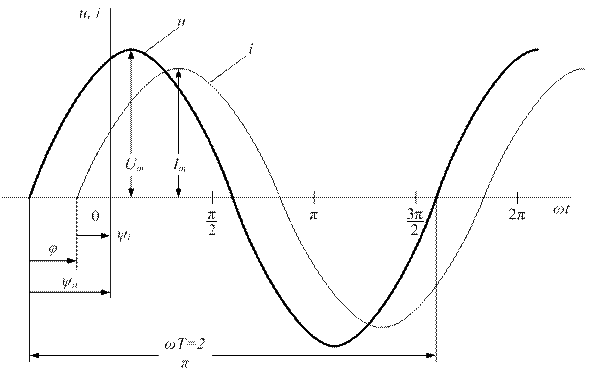
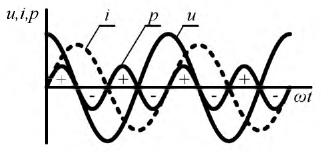
Начальная фаза ψ — величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = I ampsin(ωt); u = U ampsin(ωt)
С учётом начальной фазы:
i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)
Здесь I amp и U amp — амплитудные значения тока и напряжения.
Амплитудное значение — максимальное по модулю мгновенное значение за период.
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.
Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.
Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.
Для синусоидального тока и напряжения амплитудой I amp (U amp) среднеквадратичное значение определится из расчёта:
Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.
Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному. 
Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному. 
Для переменного синусоидального тока или напряжения коэффициент формы KФ 
Для тока и напряжения треугольной или пилообразной формы KФ 
Для переменного тока и напряжения прямоугольной формы KФ = 1
Замечания и предложения принимаются и приветствуются!
Видео:Амплитуда, размах, действующее значение. Виды значений переменного тока. Ликбез.Скачать

Решение типовых задач. Синусоидальные токи, напряжения
Синусоидальные токи, напряжения. Параметры идеальных элементов электрических цепей синусоидального тока
Общие сведения. Электромагнитный процесс в электрической цепи считается периодическим, если мгновенные значения напряжений и токов повторяются через равные промежутки времени Т. Время Т называется периодом. Напряжения u(t) = u(t+T) и токи i(t)=i(t+T) ветвей электрической цепи являются периодическими функциями времени.
Величина, обратная периоду (число периодов в единицу времени), называется частотой: f = 1/T. Частота имеет размерность 1/c, а единицей измерения частоты служит Герц (Гц).
Широкое применение в электротехнике нашли синусоидальные напряжения и токи:
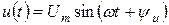
В этих выражениях:
– ω = 2π/T = 2πf – угловая частота (скорость изменения аргумента),
– ωt + ψu, ωt + ψi – фазы, соответственно напряжения и тока.
Графики изменения u(t), i(t) удобно представлять не в функции времени t, а в функции угловой величины ωt , пропорциональной t (рис. 1.1).
Величина φ = (ωt + ψu) – (ωt + ψi) = ψu, — ψi называется углом сдвига фаз. На рис. 1.1 ψu > 0, ψi > 0, φ = ψu — ψi > 0, т.е. напряжение опережает ток. Аналогично можно ввести понятие углов сдвига фаз между двумя напряжениями или токами.
Количество тепла, рассеиваемого на сопротивление R при протекании по нему тока, электромагнитная сила взаимодействия двух проводников с равными токами, пропорциональны квадрату тока. Поэтому о величине тока судят по действующему значению за период. Действующее значение периодического тока i(t) определяется по выражению
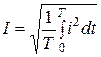
Для квадратов левой и правой частей этого равенства, после умножения их на RT, будем иметь:
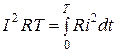
Из этого равенства следует, что действующее значение периодического тока равно по величине такому постоянному току I, который на неизменном сопротивлении R за время T выделяет тоже количество тепла, что и ток i(t).
При синусоидальном токе i(t) = Im sin ωt интеграл
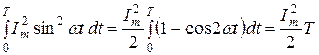
Следовательно, действующее значение синусоидального тока равно
Действующее значение синусоидальных напряжений u(t), э.д.с. e(t) определяются аналогично:
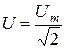
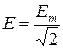
Для измерения действующих значений используются приборы электромагнитной, электродинамической, тепловой и др. систем.
Среднее значение синусоидального тока определяется как среднее за половину периода. Поэтому,
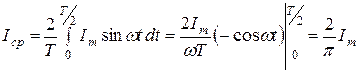
Средние значения синусоидальных напряжений u(t), э.д.с. e(t) определяются аналогично:
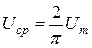
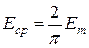
Отношение амплитудного значения к действующему называется коэффициентом амплитуды ka, а отношение действующего значения к среднему – коэффициентом формы kф. Для синусоидальных величин, например, тока i(t), эти коэффициенты равны:
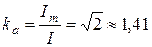
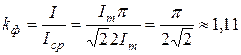
Для синусоидальных токов i(t) = Im sin(ωt + ψi) уравнения идеальных элементов R, L, C при принятых на рис. 1.2. положительных направлениях имеют вид
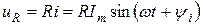
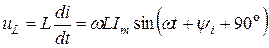
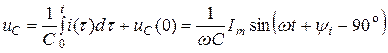
 | 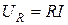 , , 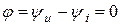 |  |
 | 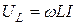 , , 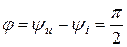 |  |
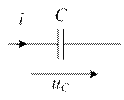 | 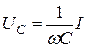 , , 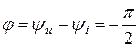 |  |
На активном сопротивлении R мгновенные значения напряжения и тока совпадают по фазе. Угол сдвига фаз φ = 0.
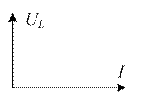
На индуктивности L мгновенное значение тока отстает от мгновенного значения напряжения на угол 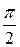
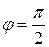
На емкости C мгновенное значение напряжения отстает от мгновенного значения тока на угол 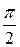
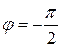
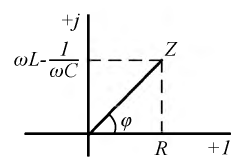
Величины ωL и 1/ωC имеют размерность [Ом] и называются реактивным сопротивлением индуктивности или индуктивным сопротивлением XL:
и реактивным сопротивлением емкости или емкостным сопротивлением XС:
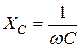
Величины 1/ωL и ωC имеют размерность [Ом -1 ] и называются реактивной проводимостью индуктивности или индуктивной проводимостью BL:
и реактивной проводимостью емкости или емкостной проводимостью BС:
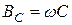
Связь между действующими значениями напряжения и тока на идеальных элементах R, L, C устанавливают уравнения:
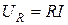
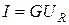
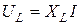
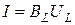
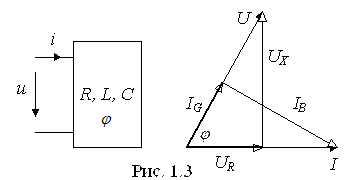
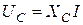
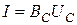
Для синусоидального напряжения u = Um sin ωt начальная фаза тока на входе пассивного двухполюсника (рис. 1.3.) равна
Проекция напряжения на линию тока
называется активной составляющей напряжения.
Проекция напряжения на линию, перпендикулярную току,
называется реактивной составляющей напряжения.
Проекция тока на линию напряжения
называется активной составляющей тока.
Проекция тока на линию, перпендикулярную напряжению,
называется реактивной составляющей тока.
Имеют место очевидные соотношения:
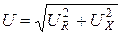
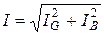
В цепи синусоидального тока для пассивного двухполюсника по определению вводятся следующие величины:
1. Полное сопротивление Z:
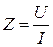
2. Эквивалентные активное Rэк и реактивное Xэк сопротивления:
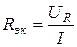
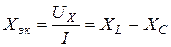
3. Полная проводимость Y:
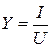
4. Эквивалентные активная Gэк и реактивная Bэк проводимости:

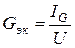
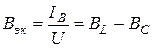
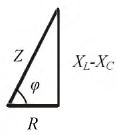
Из треугольников сопротивлений и проводимостей (рис. 1.4) следует:
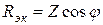
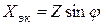
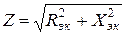
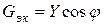
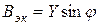
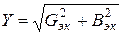
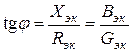
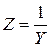
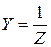
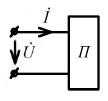
Эквивалентные параметры являются измеряемыми величинами, поэтому могут быть определены из физического эксперимента (рис. 1.5).
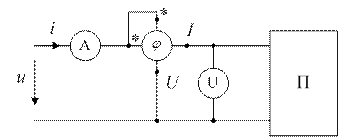
Электрическая цепь по схеме рис. 1.5 должна содержать амперметр А и вольтметр U для измерения действующих значений напряжения и тока, фазометр φ для измерения угла сдвига фаз между мгновенными значениями напряжения и тока на входе пассивного двухполюсника П.
Угол сдвига фаз пассивного двухполюсника 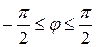
Физическая величина, численно равная среднему значению от произведения мгновенных значений напряжения u(t) и тока i(t), называется активной мощностью Р.По определению имеем:
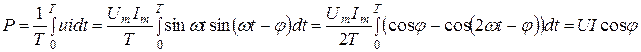
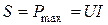
называются полной мощностью S и реактивной мощностью Q в цепи синусоидального тока. Имеет место равенство
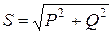
Коэффициент мощности kм в цепи синусоидального тока определяется выражением:

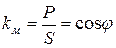
Единицей измерения активной мощности является Ватт [Вт]. Для измерения активной мощности служит ваттметр. Ваттметр включается по схеме рис. 1.6.
Единица измерения полной мощности [ВА], реактивной – [ВАр].
Для вычисления мощностей удобно использовать следующие выражения:
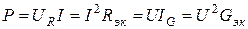
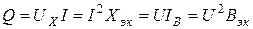
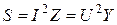
Решение типовых задач. Для измерения мгновенных значений напряжений u(t) и токов i(t) служит осциллограф. Поскольку сопротивление входа этого прибора очень большое, непосредственно для измерения тока осциллограф использовать нельзя. Измеряют не ток, а пропорциональное току напряжение на шунте Rш (рис. 1.7, а).
Задача 1.1. К источнику синусоидального напряжения частотой f = 50 Гц подключена катушка индуктивности (рис. 1.7, а). Активное сопротивление провода, из которого изготовлена катушка, R = 10 Ом, индуктивность L = 1,6 мГн. Осциллограмма напряжения uш(t) представлена на рис. 1.7, б. Сопротивление шунта Rш = 0,1 Ом. Масштаб по вертикальной оси осциллограммы mu = 0,02 В/дел (0,02 вольта на деление).
Рассчитать действующие значения напряжения uRL, составляющих uR и uL этого напряжения. Построить графики мгновенных значений напряжений uRL, составляющих uR и uL.
Решение. По осциллограмме рис. 1.7, б двойная амплитуда напряжения на шунте 2А = 10 дел. Находим амплитудное значение Im тока i:
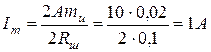
Реактивное сопротивление Х индуктивности L на частоте
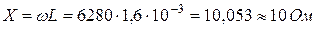
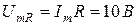
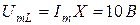
Мгновенные значения составляющих напряжения на сопротивление R катушки индуктивности и индуктивности L соответственно равны (ψi = 0):
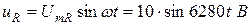
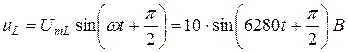
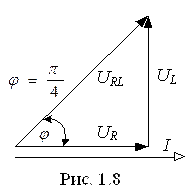
Действующие значения напряжений:
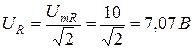
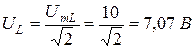
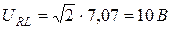
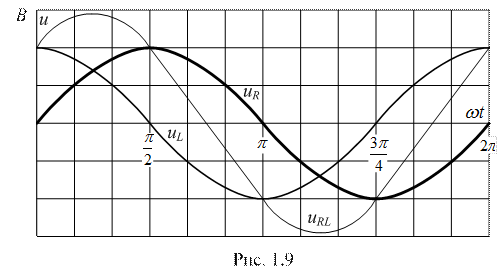
Векторные диаграммы напряжений и тока приведены на рис. 1.8.
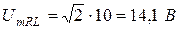
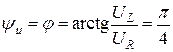
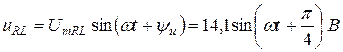
Задача 1.2. К цепи со схемой рис.1.10 приложено синусоидальное напряжение u = 141 sin 314t B.
Найти мгновенные и действующие значения тока и напряжения на всех участках цепи, если R = 30 Ом,
Решение. Назначаем положительные направления тока и напряжений как на рис. 1.10. Определяем реактивное сопротивление ХС емкости C на частоте ω = 314с -1 :
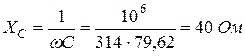
Полное сопротивление цепи:
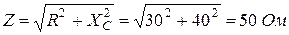
– тока i: 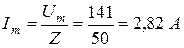
– напряжения на резисторе R: 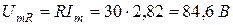
– напряжения на емкости С: 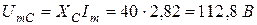
Угол сдвига фаз между напряжением u и током i:
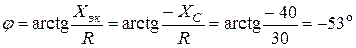
Начальная фаза тока i определяется из соотношения 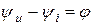
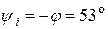
Мгновенные значения тока и напряжений на участках цепи:
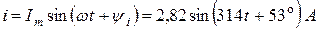
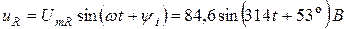
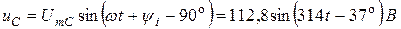
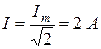
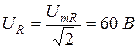
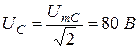
Задача 1.3. Для пассивного двухполюсника (рис. 1.5) экспериментально определены:
Найти полное и эквивалентные активное и реактивное сопротивления двухполюсника.
Решение. Имеем по определению:
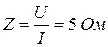
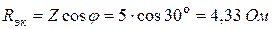
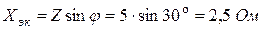
Задача 1.4 По цепи по схеме рис. 1.10 действующие значения тока i на частотах
Определить параметры цепи R и C, если на этих частотах напряжение на входе U = 100 В.
Решение. По определению на частотах f1 и f2 имеем:
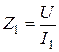
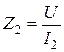
Непосредственно по схеме цепи рис. 1.10 находим:
Значения параметров R и С найдем из решения системы уравнений
Программа расчета в пакете MathCAD.
| U:=100 f1:=500 f2:=1000 I1:=1 I2:=1.8 | ←Присвоение переменным заданных условием задачи величин. |
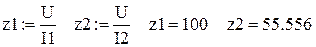 | ←Расчет полных сопротивлений на частотах f1 и f2. |
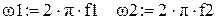 | ←Расчет угловой частоты. |
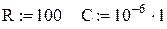 | ←Задание приближенных значений параметров R и C цепи. |
| Giver | |
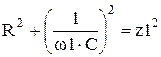 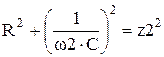 | ←Решение системы нелинейных уравнений. Для набора «=» нажмите [Ctrl]=. |
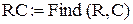 | ←Присвоение вектору RC найденных значений параметров R и C цепи. |
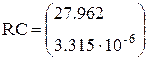 | ← 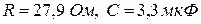 |
Значения параметров цепи: 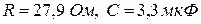
Задача 1.5. Вычислить действующее значение тока и активную мощность на входе пассивного двухполюсника с эквивалентными активной проводимостью
G = 0,011 Ом -1 и реактивной проводимостью B = 0,016 Ом -1 . Напряжение на входе двухполюсника U = 30 В.
Решение. Полная проводимость
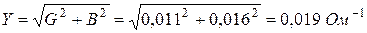
Действующее значение тока
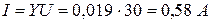
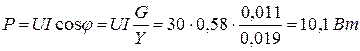
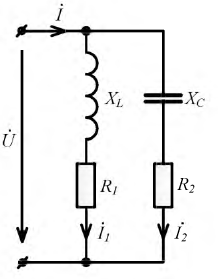
Задача 1.6. Действующее значение синусоидального тока ветви с резистором R равно 0, 1 А (рис. 1.11). Найти действующие значения напряжения u, и токов iL и i, если R = 430 Ом; XL = 600 Ом. Чему равна активная, реактивная и полная мощности этого двухполюсника?
Решение. Положительные направления напряжения и токов указаны на рис. 1.11.
Действующее значение тока IR = 0,1 А.
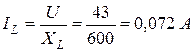
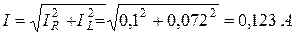
Действующее значение тока I можно вычислить, определив полную проводимость Y цепи. По виду схемы имеем
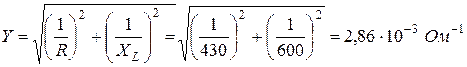
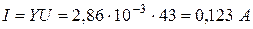
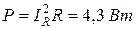
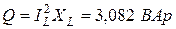
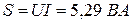
Выполняется соотношение 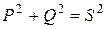
Задача 1.7. Действующее значение синусоидального напряжения на емкости С в цепи со схемой рис. 1.10 UС = 24 В. Найти действующее значение напряжения u и тока i, если XC = 12 Ом; R = 16 Ом.
Решение. Определяем действующее значение тока i
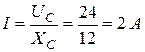
Полное сопротивление цепи
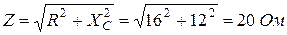
Определяем действующее значение напряжения u
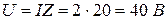
Задача 1.8. Для определения эквивалентных параметров пассивного двухполюсника в цепи синусоидального тока были сделаны измерения действующих значений напряжения, тока и активной мощности (рис. 1.12).
Для определения характера реактивного сопротивления (проводимости) параллельно двухполюснику была включена емкость С (ВС ? Вэк). При этом показания амперметра уменьшились. Рассчитать эквивалентные сопротивления и проводимости двухполюсника.
Решение.
Действующее значение: I = 0,5 A, U = 100 B. Активная мощность, потребляемая двухполюсником, P = 30 Вт. Полное сопротивление двухполюсника
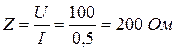
Эквивалентное активное сопротивление
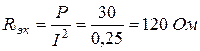
Эквивалентное реактивное сопротивление
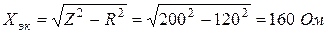
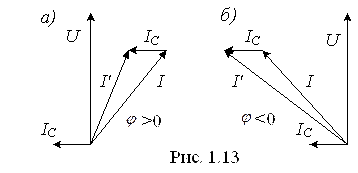
Полная проводимость двухполюсника
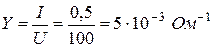
Эквивалентная активная проводимость
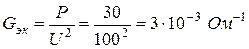
Эквивалентная реактивная проводимость
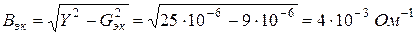
Следует обратить внимание, что треугольники сопротивлений и проводимостей для одного и того же двухполюсника подобны (рис. 1.4). Поэтому,
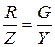
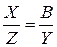
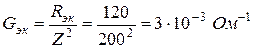
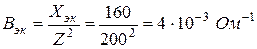
1.3. Задачи и вопросы для самоконтроля
1. Какими параметрами описываются синусоидальные токи в электрических цепях?
2. Как связаны между собой круговая частота ω и период Т синусоидального тока?
3. Что такое действующее значение переменного тока?
4. Запишите формулы для вычисления индуктивного и емкостного сопротивлений.
5. Объясните, как определить напряжение на участке цепи, если заданы 
6. Нарисуйте треугольник сопротивлений и треугольник проводимостей с необходимыми обозначениями.
7. Запишите формулы для вычисления активной и реактивной мощностей.
8. Напряжение на индуктивности L = 0,1 Гн в цепи синусоидального тока изменяется по закону 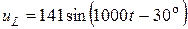
9. Ток в емкости С = 0,1 мкФ равен 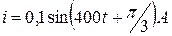
10. На участке цепи с последовательно включенными активным сопротивлением R = 160 Ом и емкостью С = 26,54 мкФ мгновенное значение синусоидального тока 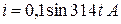
Дата добавления: 2016-01-29 ; просмотров: 102122 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Однофазные цепи синусоидального тока
Содержание:
Основные определения, понятия и законы в теории электрических цепей:
Электрическая цепь — это совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования электрической энергии, если процессы, протекающие в этих устройствах, могут быть определены с помощью понятий ЭДС, тока и напряжения, которые могут быть как постоянными
Электрическая схема — это изображение электрической цепи с помощью условных обозначений. Несмотря на всё многообразие цепей, каждая из них содержит элементы двух основных типов — это источники и потребители.
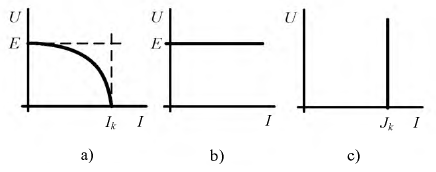
Источники энергии (см. рис. 1.1) могут быть двух типов: источники ЭДС (напряжения) и источники тока.
Рис. 1.1. Реальные источник ЭДС (a) и источник тока (b)
Источник тока характеризуется величиной тока 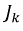
Источник напряжения характеризуется двумя основными параметрами: величиной ЭДС 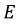
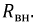
Для источника ЭДС положительное направление 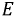
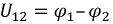
Если внутренним сопротивлением источника можно пренебречь 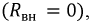
Другим вариантом идеального источника энергии является источник тока, для которого 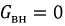
Рис. 1.2. Вольт-амперные характеристики а) реального источника ЭДС, b) идеального источника ЭДС, c) идеального источника тока
Поскольку физические свойства идеальных источников коренным образом различны, то прямая их замена друг на друга невозможна. Тем не менее, процедура преобразования одного реального источника в другой возможна и широко применяется в расчетах. Например, при замене реального источника тока в реальный источник ЭДС его параметры равны:
По своим физическим свойствам элементы электрических цепей могут характеризоваться такими параметрами, как сопротивление 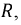
Рис. 1.3. Потребители в электрических цепях
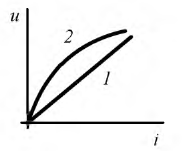
Под идеализированным резистивным элементом цепи (в дальнейшем для краткости — сопротивление 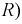
Вольт-амперные характеристики (В.А.Х.) линейного (1) и нелинейного (2) сопротивлений изображены на рис. 1.4.
Рис. 1.4. Вольт-амперные характеристики линейного (1) и нелинейного (2) сопротивлений
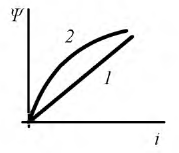
Под идеализированным индуктивным элементом электрической цепи (в дальнейшем для краткости — индуктивность 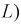
где 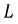
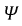
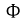
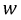
Вебер-амперные характеристики линейной (1) и нелинейной (2) индуктивности представлены на рис. 1.5.
Рис. 1.5. Вебер-амперные характеристики линейной (1) и нелинейной (2) индуктивности
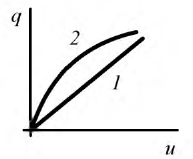
Под идеализированным емкостным элементом электрической цепи (в дальнейшем для краткости — емкость 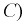
где 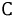
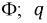
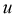
Кулон-вольтные характеристики линейной (1) и нелинейной (2) емкости представлены на рис. 1 .6.
Рис. 1.6. Кулон-вольтные характеристики линейной (1) и нелинейной (2) емкости
Любая цепь характеризуется следующими основными топологическими понятиями.
Ветвь — это участок цепи, составленный из последовательно соединенных элементов цепи и расположенный между двумя узлами.
Узел — это точка цепи, где сходятся три или более ветвей.
Контур — это любой замкнутый путь (рис. 1.7.), проходящий по нескольким ветвям.
Рис. 1.7. Электрический контур
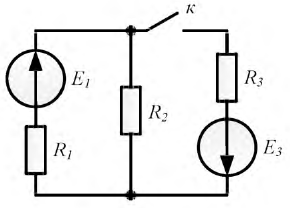
Контур называется независимым, если в его составе присутствует хотя бы одна новая ветвь, ранее не входившая в другие контуры. В схеме на рис 1.7 при замкнутом ключе имеем три контура, но лишь два из них независимы.
Видео:Урок 25. Что такое Переменный ТОК | Практические примерыСкачать

Закон Ома
Закон Ома для пассивного участка цепи при постоянных токах имеет вид:
Рассмотрим участок цепи с ЭДС (рис. 1.8).
Рис. 1.8. Линейный участок цепи, содержащий ЭДС
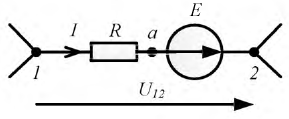
Из состава сложной электрической цепи выделим ветвь, содержащую источник энергии и потребитель. Для определенности примем, что направления тока и источника ЭДС совпадают.
При условно выбранных положительных направлениях тока и ЭДС в ветви имеем:
Вычтем из уравнения (1.5) уравнение (1.6) и тогда получим
Полученное выражение представляет собой закон Ома для участка цепи с ЭДС. В случае несовпадения направления тока в ветви с направлениями напряжения и ЭДС перед ними появляется знак «минус».
Видео:Фаза, начальная фаза и угловая частота переменного токаСкачать

Законы Кирхгофа
Первый закон Кирхгофа — алгебраическая сумма токов в узле равна нулю:
где 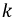
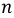
Второй закон Кирхгофа — алгебраическая сумма падений напряжений вдоль любого замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре:
Уравнение баланса мощности:
где 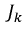
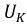
Уравнение баланса мощности является модификацией закона сохранения энергии для электрических цепей. Это базовое уравнение для проверки правильности выполненных расчетов тех или иных цепей. В левой части этого уравнения стоит арифметическая сумма мощностей, потребляемых приёмниками. В правой части — мощность, отданная источниками в цепь.
При этом возможна такая ситуация, когда одно из слагаемых суммы справа может оказаться отрицательным. Это будет означать, что в данной ситуации источник становится потребителем. Она возникает в случае, когда ток и ЭДС источника направлены встречно, например, зарядка аккумулятора.
Видео:лекция 407 действующее значение напряженияСкачать

Цепи однофазного синусоидального тока и напряжения
Рассмотренные выше источники энергии могут быть источниками постоянного или переменного напряжения (тока), причём закон изменения во времени источников переменного напряжения (тока) может носить как периодический, так и непериодический характер. Наибольшее практическое распространение получили источники, а, следовательно, и цепи, электромагнитные процессы в которых подчиняются периодическому закону.
Частным случаем таких цепей являются цепи однофазного синусоидального тока.
Мгновенное значение любой синусоидальной функции: напряжения, тока, ЭДС и т.д. может быть представлено выражением вида:
где 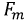
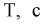
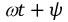
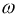
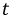
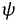
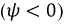
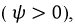
Период 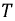
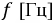
а круговая(циклическая) частота:
Рис. 2.1. График периодической функции напряжения
Среднее и действующее значения периодической функции (тока и напряжения)
Средней величиной переменного тока (ЭДС, напряжения) называется среднее арифметическое из всех мгновенных величин за полупериод. Согласно определению:
где 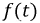
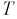
Ввиду симметричности синусоиды получаем, что среднее ее значение за период равно нулю, поэтому вводят понятие среднего значения за половину периода:
Например, для синусоидального тока, его среднее значение будет равно:
Значительно большее значение имеет понятие действующего значения периодических функций. Определим количество тепла, выделенное за период 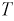
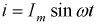
Для переменного тока:
Для постоянного тока:
Приравняв правые части уравнений, получим:
где 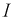
На рис. 2.2. пунктирной линией изображено действующее значение синусоидального тока.
Рис. 2.2. Синусоидальная функция тока и ее действующее значение
Элементы R, L, C в цепях синусоидального тока
Синусоидальный ток в резистивном элементе:
Пусть ток в этом элементе изменяется по закону 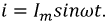
Рис. 2.3. Условно положительные направления тока и напряжения на сопротивлении
Определим напряжение, действующее на зажимах резистивного элемента на основании закона Ома:
Полученный результат показывает, что напряжение изменяется в фазе с током.
Определим мгновенную мощность, потребляемую сопротивлением
где 
Из графика мгновенной мощности (рис. 2.4) следует, что она не отрицательна 
Рис. 2.4. Графики мгновенных значений напряжения, тока и мощности на сопротивлении
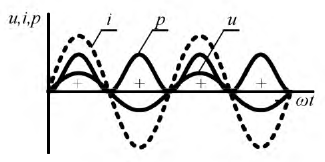
Для оценки потребляемой приемником мощности вводят понятие средней мощности за период:
где 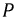
Синусоидальный ток в индуктивном элементе
Пусть ток в этом элементе изменяется по закону:
На рис. 2.5 показаны условно положительные направления тока, напряжения и ЭДС самоиндукции.
Определим напряжения на индуктивности 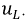
где 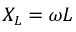
Рис. 2.5. Условно положительные направления тока, напряжения и ЭДС самоиндукции
Напряжение на индуктивности опережает ток на
Мгновенная мощность на индуктивности:
Среднее значение мощности за период:
Для оценки запасенной в индуктивности энергии магнитного поля вводят понятие реактивной (индуктивной) мощности
где 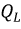
Из графика мгновенной мощности (рис. 2.6) следует, что положительная полуволна мощности соответствует потреблению энергии из сети, а отрицательная — ее возврату в сеть.
Энергия, потребляемая индуктивностью, работы не совершает.
Рис. 2.6. Графики мгновенных значений напряжения, тока и мощности на индуктивности
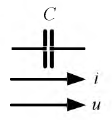
Синусоидальный ток в емкостном элементе
Пусть ток в этом элементе изменяется по закону:
На рис. 2.7 показаны условные положительные направления тока и напряжения на емкости.
Рис. 2.7. Условно положительные направления тока и напряжения на емкости
где 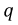
Для линейной емкости 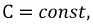
называется емкостным сопротивлением, Ом.
Ток в ёмкости опережает приложенное напряжение на угол 90°, также можно считать, что напряжение отстаёт от тока на 90°.
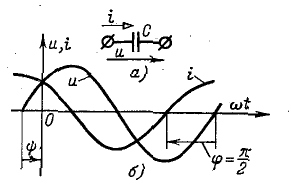
Определим мгновенную мощность:
Среднее значение мощности за период:
Таким образом, идеальная емкость не потребляет из сети активную мощность. Для оценки запасенной в емкости энергии электрического поля вводят понятие реактивной мощности:
Графики функций тока, напряжения и мгновенной мощности представлены на рис. 2.8. Если 
Рис. 2.8. Графики мгновенных значений тока, напряжения и мощности на емкости
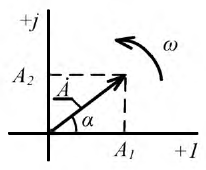
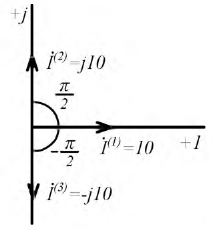
Изображение синусоидальных функций времени (напряжение, сила тока) векторами на комплексной плоскости
Расчет сложной разветвленной цепи может быть существенно упрощен, если представить синусоидальные токи и напряжения векторами, расположенными на комплексной плоскости. Такой метод получил название метода комплексных амплитуд.
В основе этого метода лежит формула Эйлера:
где 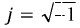
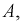
где 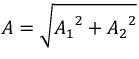
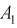
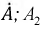
Поскольку в формуле Эйлера угол 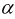
Полученный результат показывает (2.24), что синусоидальная функция времени есть мнимая часть некоторой комплексной функции 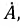
Рис. 2.9. Изображение вектора 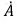
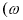
Положив, что 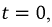
Векторная диаграмма — диаграмма векторов на комплексной плоскости, построенная с учетом их взаимной ориентации по фазе.
Если векторы вращаются на плоскости с одинаковыми частотами 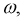
В качестве примера на рис. 2.10 изображена операция умножения некоторого вектора 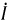
Рис. 2.10. Умножение вектора на 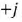
Пусть модуль 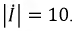
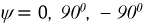
Основы символического (комплексного) метода расчета цепей синусоидального тока
Цепь, составленная из разнородных элементов, описывается системой дифференциальных уравнений, решение которой при синусоидальных токах и напряжениях затруднительно. Комплексный метод расчета позволяет перейти от тригонометрических уравнений, составленных для мгновенных токов, напряжений и других величин, к алгебраическим уравнениям, составленным для соответствующих им комплексным изображениям.
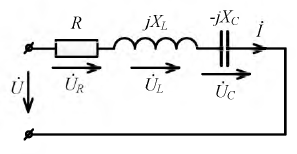
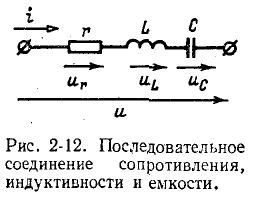
Последовательное соединение элементов R L C
На рис. 2.11 изображена схема с последовательным соединением активного 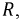
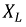
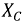
Рис. 2.11. Последовательное соединение элементов
Схема (рис. 2.11) на основании второго закона Кирхгофа для мгновенных величин описывается уравнением:
Перейдем к комплексным изображениям. Пусть мгновенный ток и его комплексное изображение изменяются по закону:
Используя полученный комплекс тока, определим комплексы действующих значений падений напряжений на участках цепи: для сопротивления:
Найденные комплексы 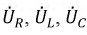
Выражение (2.32) представляет собой закон Ома в комплексной форме. В знаменателе — комплексное сопротивление рассматриваемой цепи, которое имеет вещественную и мнимую составляющую:
На рис. 2.12 сопротивление 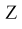
Рис. 2.12. Изображение сопротивления 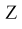
Для комплексных амплитуд закон Ома запишется в следующем виде:
где 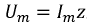
Аргумент комплексного сопротивления:
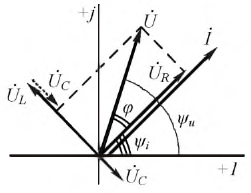
Построим векторную диаграмму цепи (рис. 2.13), приняв для определенности, что
Рис. 2.13. Векторная диаграмма для последовательного колебательного контура
Полагая, что ток и напряжение изменяются по законам:
и, заменив их комплексными изображениями, начнем построение векторной диаграммы с вектора тока, т.к. он одинаков на всех участках цепи. На основании уравнений 2.28-2.30 вектор 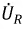
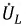
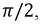
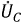
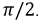
Рис. 2.14. Векторный треугольник напряжений
Ниже на рис. 2.15 приведен треугольник сопротивлений.
Рис. 2.15. Скалярный треугольник сопротивлений
Угол сдвига фаз между током и напряжением можно определить из любого треугольника:
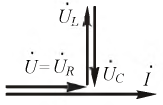
Резонанс напряжений
Резонансом в цепях переменного тока, содержащих индуктивные и емкостные элементы, называется явление совпадения по фазе векторов тока и напряжения на входе цепи или на участке цепи, при этом
Резонанс напряжений наблюдается в последовательном колебательном контуре. На рис. 2.16 приведена векторная диаграмма для этого режима.
Рис. 2.16. Векторная диаграмма резонансного режима
При резонансе реализуется равенство:
где 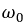
Резонанс достигается путем изменения одного из параметров 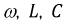
Определим индуктивное и емкостное сопротивления цепи при резонансе:
Величина 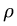
Введем еще один важный параметр, характеризующий резонанс — добротность контура:
Добротность (коэффициент резонанса) — это отношение напряжения на индуктивности или на емкости при резонансе к входному напряжению цепи.
Рассмотрим энергетические соотношения в цепи при резонансе напряжений. Определим суммарную энергию, потребляемую реактивными элементами из сети:
Таким образом, суммарная энергия электрического и магнитного полей при резонансе остается величиной постоянной:
Частотные характеристики последовательного колебательного контура
Рассмотрим частотные характеристики цепи в последовательном колебательном контуре. Пусть к данной электрической цепи подведено синусоидальное напряжение с частотой 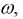
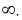
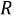
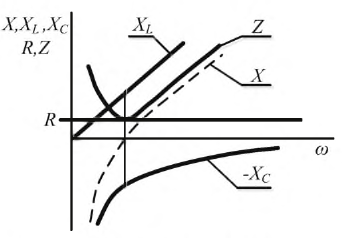
Построим функции названных выше сопротивлений в одних координатных осях (рис. 2.17).
Рис. 2.17. Зависимости сопротивлений цепи от частоты
Исходя из построений, можно заключить, что в дорезонансной области частот 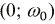
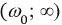
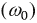
Рис. 2.18. Кривые изменений напряжений, тока и фазы от частоты
На нулевой частоте (источник постоянной ЭДС) индуктивность заменяется короткозамкнутым проводником, а емкость — разрывом; на бесконечной частоте свойства указанных элементов меняются местами.
Значения функции 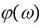
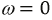
Оценим влияние параметров цепи на форму резонансной кривой тока. Решение этого вопроса начнем с сопротивления последовательного колебательного контура, выполнив с ним следующие преобразования:
Используя полученное выражение для входного сопротивления 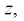
где 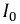
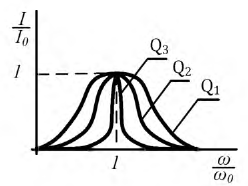
Резонансные кривые в соответствии с (2.42) приведены на рис. 2.19 в относительные единицах:
Рис. 2.19. Резонансные кривые
Построенные зависимости показывают, что чем больше добротность 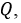
Параллельное соединение элементов R L C
Рассмотрим параллельное соединение активного 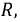
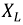
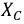
Рис. 2.20. Схема параллельного соединения элементов
Пусть на вход цепи подано напряжение 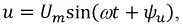
Комплексное изображение входного напряжения:
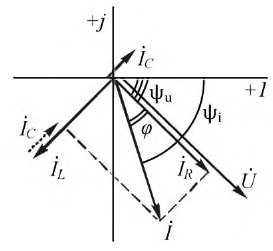
Для определения комплекса общего тока найдем его составляющие:
тогда комплекс общего тока:
Построим векторную диаграмму на комплексной плоскости для параллельного соединения (рис. 2.21).
Рис. 2.21. Векторная диаграмма параллельного соединения разнородных элементов
Пусть 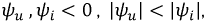
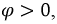
Выражение в скобках (2.43) имеет размерность 1/Ом или См (сименс) и носит название комплексной проводимости цепи:
где 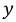
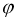
Комплексная амплитуда общего тока:
Мгновенное значение общего тока:
Под комплексной проводимостью любой цепи понимается величина, обратная ее полному комплексному сопротивлению:
где 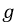
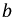
где 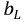
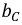
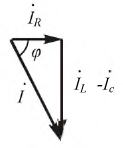
Из векторной диаграммы рис. 2.21 можно выделить треугольник токов (рис. 2.22).
Рис. 2.22. Векторный треугольник токов
Разделив стороны векторного треугольника токов на вектор напряжения, получим скалярный треугольник проводимостей (рис. 2.23).
Рис. 2.23. Скалярный треугольник проводимостей
В качестве примера для ветви, изображенной на рис. 2.24, определим ее активную и реактивную проводимости.
Рис. 2.24. Участок цепи с активно-индуктивным сопротивлением
В полученном выражении проводимости ветви имеем: 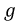
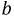
Резонанс токов
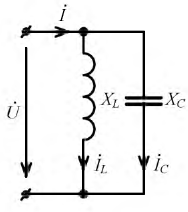
Резонансный режим, возникающий при параллельном соединении элементов 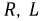
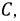
Рис. 2.25. Цепь с параллельным соединением разнородных приемников
В цепи по рис. 2.25 режим резонанса токов возникает при условии равенства нулю результирующей реактивной проводимости этой цепи, т.е.:
Реактивные проводимости ветвей соответственно равны:
Подставим выражения 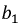
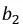
и после преобразования получим резонансную частоту:
Анализ полученного уравнения показывает, что существует четыре возможных варианта значений частоты
1. Если 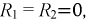
2. Если 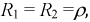
С физической точки зрения это означает, что входное сопротивление данного контура равно ее волновому сопротивлению, которое не зависит от частоты, а значит, резонанс будет иметь место при любой частоте источника. Для доказательства этого положения определим входное сопротивление цепи:
3. Если 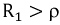
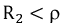
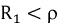
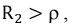
4. Если 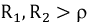
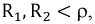
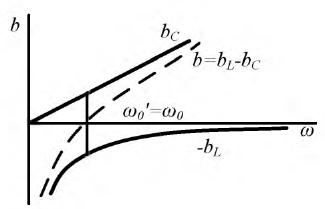
Частотные характеристики параллельного колебательного контура
Для простоты рассмотрим идеальный контур, то есть контур без потерь (рис. 2.26).
Рис. 2.26. Параллельный колебательный контур
На рис. 2.27 построены частотные характеристики реактивных проводимостей 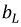
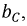
Рис. 2.27. Частотные характеристики параллельного колебательного контура
При изменении частоты от нуля до бесконечности параллельный колебательный контур имеет индуктивный характер до резонансной частоты и ёмкостный характер в послерезонансном диапазоне частот.
Ток в неразветвленной части цепи:
График тока (рис. 2.28), изображенный сплошной линией, говорит о том, что при резонансе общий ток, потребляемый цепью, равен нулю, несмотря на наличие токов в ветвях, что, в свою очередь, подтверждается векторной диаграммой (рис. 2.29).
Рис. 2.28. График зависимости тока в неразветвленной части цепи от частоты
Рис. 2.29. Векторная диаграмма для резонансного режима идеального параллельного контура
При учете сколь угодно малого активного сопротивления цепи ток при резонансе не равен нулю. Пунктирная кривая изображает реальный ток в цепи.
Мощность в цепи синусоидального тока
Рассчитаем мощность произвольного приемника, представленного на рис. 2.30 в виде пассивного двухполюсника
Рис. 2.30. Пассивный двухполюсник
Пусть 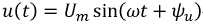
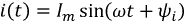
Тогда мгновенная мощность, потребляемая двухполюсником 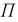
Построим график полученной функции 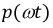
Рис. 2.31. Зависимость мгновенных значений тока, напряжения и мощности пассивного двухполюсника
Полученный график говорит о том, что функция мгновенной мощности знакопеременна, причем амплитуда положительной полуволны больше амплитуды отрицательной полуволны. Это значит, что двухполюсник имеет активно-реактивный характер. Если бы двухполюсник не содержал реактивных элементов, то график полностью бы лежал над осью 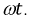
Эта мощность называется активной мощностью. Наряду с активной вводится понятие полной мощности:
Единица измерения полной мощности — вольт-ампер
Разность полной и активной мощности, обусловленная наличием реактивных (индуктивных и емкостных) элементов, называется реактивной мощностью:
Единица измерения реактивной мощности — вольт-ампер реактивный [вар]. Мощности связаны между собой соотношением:
Треугольник мощностей (рис. 2.32.а) можно получить из векторной диаграммы напряжений (см. рис. 2.14), умножив все стороны треугольника напряжений на вектор тока
В этом треугольнике:
сторона
сторона
сторона
Рис. 2.32. Треугольники мощностей на основе векторной диаграммы напряжений (а) и векторной диаграммы токов (b)
Аналогичный треугольник мощностей по рис. 2.32. b можно получить из векторной диаграммы токов (рис. 2.22), умножив все стороны треугольника токов на вектор
сторона
сторона
сторона
Выражение мощности в комплексной форме
Пусть на входе некоторого двухполюсника известны комплексные изображения напряжения и тока:
Мощность в комплексной форме выражается в виде произведения:
где 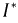
При умножении комплекса напряжения на сопряженный комплекс тока аргумент мощности получится равным
Передача энергии от активного двухполюсника к пассивному
При работе любой электрической цепи должен иметь место баланс мощностей, т.е. алгебраические суммы активных и реактивных мощностей, развиваемых генераторами, должны равняться алгебраическим суммам активных и реактивных мощностей, потребляемых во всех пассивных элементах цепи, включая и внутренние сопротивления генераторов.
Полная мощность, развиваемая генератором:
Полная мощность, потребляемая любым приемником:
Тогда уравнение баланса мощностей:
где 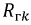
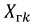
Пусть в электрической цепи работает один источник энергии. Оценим условия, при которых в нагрузке будет выделяться максимальная мощность. Ток в цепи:
Реактивное сопротивление цепи должно равняться нулю:
т.е. цепь должна работать в резонансном режиме, и, следовательно, 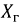
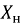
Найдем соотношение между сопротивлениями 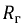
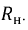
и, полагая, что сопротивление нагрузки 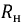
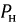
Следовательно, для получения максимальной мощности в нагрузке необходимо, чтобы:
т.е., сопротивления генератора и нагрузки должны быть комплексно сопряженными величинами. Режим работы цепи при этом условии называется согласованным режимом. КПД источника при этом условии:
При столь низком КПД согласованный режим работы используется только в слаботочных цепях, таких, например, как телефонные линии связи, линии автоматики и управления и т.д., где важна величина полезного сигнала по сравнению с помехами.
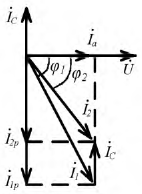
Коэффициент мощности
Наибольшие действующие значения напряжения и тока, допускаемые для генераторов и трансформаторов, производящих и, соответственно, преобразующих электрическую энергию, зависят от их конструкции, а наибольшая мощность, которую они могут развивать, не подвергаясь опасности быть поврежденными, определяется произведением этих значений. Поэтому рациональное использование электрических машин и трансформаторов может быть достигнуто лишь в том случае, когда приёмники электрической энергии обладают высоким коэффициентом мощности
Подавляющее большинство потребителей энергии носит активноиндуктивный характер, т.е. 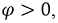
Для улучшения (увеличения) 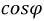
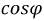
Пусть суммарная активная мощность приемников:
При увеличении 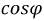
Следовательно,
Проиллюстрируем расчет необходимой величины емкости для повышения коэффициента мощности до значения 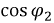
Рис. 2.33. Векторная диаграмма, иллюстрирующая повышение коэффициента мощности
Рассчитаем необходимый емкостный ток по выражению:
Такую же роль, как конденсаторы, могут играть синхронные двигатели, работающие в «перевозбужденном» режиме. Они при этом потребляют из сети ток, реактивная составляющая которого носит емкостной характер.
Видео:Переменный ток, действующее значение силы тока и напряженияСкачать

Электрическая цепь однофазного синусоидального тока
Синусоидальные электрические величины:
Электромагнитный процесс в электрической цепи, при котором мгновенные значения напряжений и токов повторяются через равные промежутки времени, называется периодическим. Наименьшее время, по истечении которого мгновенные значения периодической величины повторяются, называется периодом. Если величину, являющуюся периодической функцией времени t, обозначить через F (t), то для любого положительного или отрицательного значения аргумента t справедливо равенство
Геометрически это значит, что ординаты двух произвольных точек графика F (t) с абсциссами, различающимися на Т, одинаковы.
Величина, обратная периоду, т. е. число периодов в единицу времени, называется частотой:
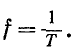
Единицей измерения частоты служит герц (Гц); частота равна 1 Гц, если период равен 1 с.
Преобладающим видом периодического процесса в электрических цепях является синусоидальный режим, характеризующийся тем, что все напряжения и токи являются синусоидальными функциями одинаковой частоты. Это возможно только при заданных синусоидальных э. д. с. и токах источников. Тем самым обеспечивается наиболее выгодный эксплуатационный режим работы электрических установок.
Как известно из курса математического анализа, синусоида является простейшей периодической функцией; всякие другие несинусоидальные периодические функции могут быть разложены в бесконечный ряд синусоид, имеющих кратные частоты. Поэтому для исследования процессов в цепях переменного тока в первую очередь необходимо изучить особенности цепей синусоидального тока.
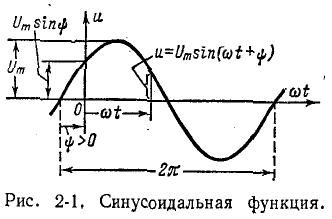
На рис. 2-1 изображена синусоидальная функция
здесь 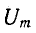
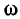
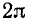
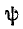
Начальная фаза 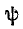
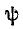
Косинусоида может рассматриваться как синусоида с начальной фазой 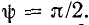
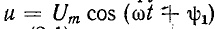
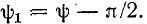
За аргумент функции (2-1) может быть принято время t или соответственно угол 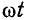
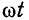
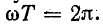
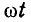
Если угол 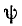
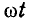
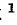
Величина 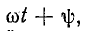
Рассмотренные в данном параграфе понятия, характеризующие синусоидальные электрические величины, являются исходными при изучении электрических процессов в цепях переменного тока.
Генерирование синусоидальной э. д. с.
Наиболее распространенным в промышленности способом получения синусоидального тока является применение электромагнитных машин, так называемых синхронных генераторов, приводимых во вращение тепловыми, газовыми, гидравлическими или другими двигателями.
Генератор переменного тока состоит из двух частей — неподвижного статора и вращающегося ротора.
1 Напомним, что 1 рад = 57,3°.
На одном из них (чаще на роторе) располагаются полюсы, т. е. электромагниты, обмотка которых питается от источника постоянного напряжения, или постоянные магниты. На другом (обычно на статоре) располагается главная обмотка, в которой наводится переменная э. д. с.
Генератор может иметь одну или несколько пар полюсов. На рис. 2-2, а упрощенно показан явнополюсный генератор с двумя парами полюсов, размещенных на роторе. Указанному на рис. 2-2, а положению ротора относительно статора соответствует на рис. 2-2, б развернутая на плоскость схема расположения обмотки и полюсов.
В каждом проводе обмотки, находящемся в пазу статора, при вращении ротора наводится по закону Фарадея
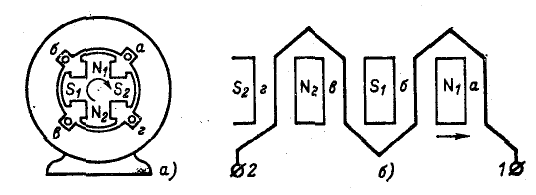
Рис. 2-2, Принцип устройства синхронного генератора,
э. д. с. 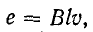
При постоянных значениях 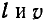
В момент времени, которому соответствует указанное на рис. 2-2 положение ротора, магнитная индукция под проводом равна нулю и поэтому э. д. с. е также равна нулю.
После поворота ротора на одну восьмую часть полного оборота (половина полюсного шага) э. д. с. достигнет максимума и будет направлена от вывода 1 к выводу 2 (по правилу правой руки) 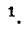
При числе пар полюсов р и числе оборотов ротора в минуту п частота наводимой переменной э. д. с. в герцах равна:
В энергосистемах СССР и большинства других стран частота промышленного тока равна 50 Гц. В США принята частота 60 Гц.
В авиации с целью уменьшения массы оборудования применяются машины с повышенной частотой вращения. Частота / при этом получается повышенной (400 Гц). Например, генератор, имеющий р = 2 и n = 12 000 об/мин, генерирует синусоидальную э. д. с. с частотой
При большой окружной скорости 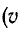
Проводная связь использует частоты порядка 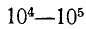
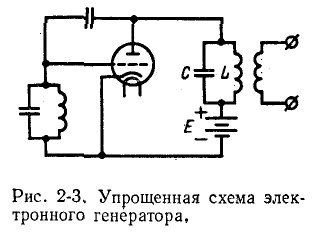
На рис. 2-3 в виде примера показана одна из схем электронного генератора высокой частоты. Анод трехэлектродной лампы (триода) присоединен через контур LC к положительному полюсу источника постоянного напряжения, например аккумуляторной батареи. В контуpe LC, называемом резонансным, возникают незатухающие синусоидальные колебания тока, частота которых зависит от выбора параметров L и С. 
Аналогично по правилу левой руки большой палец указывает направление силы, действующей на проводник с током.
Электрическая энергия, необходимая для поддержания этих колебаний, поступает от аккумуляторной батареи.
Работа электронных генераторов здесь не рассматривается. Процессам, происходящим в резонансных цепях5. Принцип действия электронных генераторов разобран во второй части курса. Приведенная выше схема электронного генератора предназначена для получения синусоидальных колебаний высокой частоты.
Начало практического внедрения переменного тока относится ко втррой половине XIX в., когда выдающийся русский электротехник Павел Николаевич Яблочков (1847—1894) стал применять на практике изобретенные им электрические свечи.
Среднее и действующее значения функции
Среднее значение периодической функции f (t) за период Т определяется по формуле
Отсюда видно, что среднее значение за период равно высоте прямоугольника с основанием Т, площадь которого равна площади, ограниченной функцией f (t) и осью абсцисс за один период.
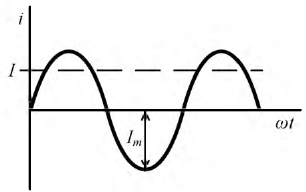
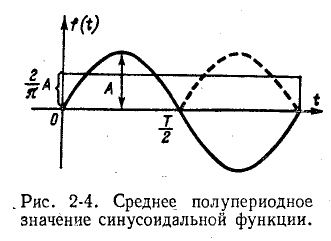
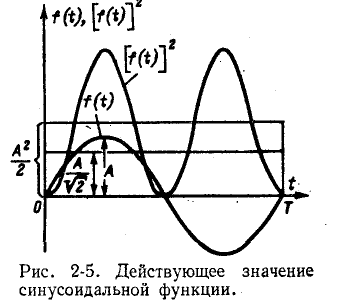
В случае синусоидальной функции среднее значение за период равно нулю, так как площадь положительной полуволны компенсируется площадью отрицательной полуволны синусоиды. Поэтому здесь пользуются понятием среднего значения функции, взятой по абсолютному значению или, что то же, среднегополупериодного значения, соответствующего положительной полуволне синусоиды (рис. 2-4).
В соответствии с этим среднее значение синусоидального тока с амплитудой А — 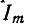
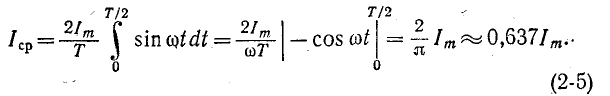
Аналогично среднее значение синусоидального напряжения
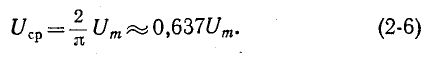
Измерительные приборы магнитоэлектрической системы реагируют на средние значения за период. Для измерения среднего полупериодного значения, соответствующего положительной полуволне, синусоидальный ток предварительно пропускается через выпрямительное устройство.
Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым проходит один и тот же ток, пропорциональны квадрату тока. Поэтому о величине тока судят обычно по так называемому действующему 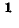
Действующее значение периодической функции 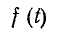
Из этой формулы следует, что величина F2 представляет собой.среднее значение функции 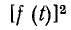
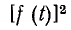
ныне не рекомендуемый термин «эффективное» значение,
В соответствии с (2-7) действующий периодический ток
Возведя (2-8) в квадрат и умножив обе части полученного выражения на rТ, найдем:
Это равенство показывает, что действующий периодический ток равен такому постоянному току, который, проходя через неизменное сопротивление r, за период времени Т выделяет то же количество тепла, что и данный ток i.
Аналогично действующее периодическое напряжение 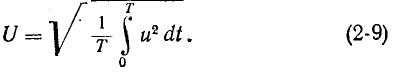
При синусоидальном токе
Следовательно, согласно (2-8)
Аналогично действующее синусоидальное напряжение
Номинальные токи и напряжения электротехнических устройств определяются, как правило, действующими значениями; поэтому действующие значения представляют наиболее распространенный электрический параметр.
Для измерения действующих значений применяются системы приборов тепловая, электромагнитная, электродинамическая и др.
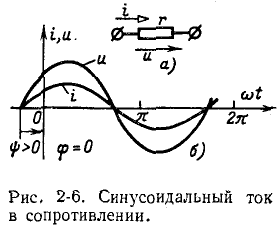
Синусоидальный ток в сопротивлении
Если синусоидальное напряжение 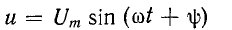
Следовательно, напряжение на выводах сопротивления и ток, проходящий через это сопротивление, имеют
одинаковую начальную фазу, или, как говорят, совпадают по фазе: они
одновременно достигают своих амплитудных значений 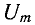
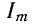
Разность начальных фаз двух синусоид, имеющих одинаковую частоту, называется фазовым сдвигом. В данном случае фазовый сдвиг между напряжением и и током i равен нулю:
При прохождении синусоидального тока через сопротивление г не только мгновенные напряжения на сопротивлении и тока в нем, но и амплитуды и соответственно действующие напряжение и ток связаны законом Ома:
Пользуясь величиной проводимости 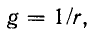
Мгновенная мощность, поступающая в сопротивление:
изменяется с угловой частотой, удвоенной по сравнению с частотой напряжения и тока, и колеблется в пределах от 0 до 2UI (рис. 2-7).
Как видно из (2-10), кривая 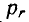
Ввиду того что в рассматриваемом случае напряжение и ток совпадают по фазе, т. е. всегда имеют одинаковый знак (плюс или минус), их произведение всегда положительно.
Среднее значение мощности за период Р 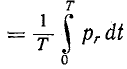
В рассматриваемом случае, как это видно из
выражения (2-10) и рис. 2-7, активная мощность Р 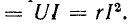
Сопротивление r в свою очередь может быть определено как отношение активной мощности к квадрату действующего значения тока:
Отмечалось, что сопротивление проводника при переменном токе больше, чем при постоянном токе, вследствие явлений поверхностного эффекта, возникновения вихревых токов и излучения электромагнитной энергии в пространство (при высоких частотах). В отличие от сопротивления при постоянном токе сопротивление проводника при переменном токе называется активным сопротивлением.
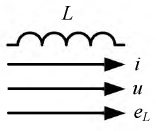
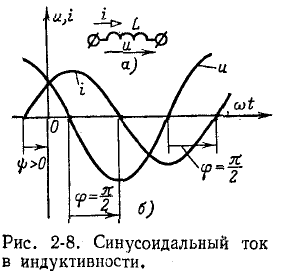
Синусоидальный ток в индуктивности
Пусть через индуктивность L (рис. 2-8, а) проходит ток
Электродвижущая сила самоиндукции определяется по формуле (1-3):
Значит, напряжение на индуктивности
Полученное выражение показывает, что напряжение на индуктивности опережает ток на угол, 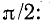
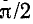
Под фазовым сдвигом 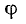
Амплитуды, так же как и действующие значения напряжения и тока, связаны соотношением, подобным закону Ома:
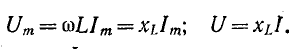
Величина 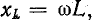
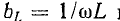
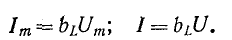
Индуктивное сопротивление представляет собой расчетную величину, с помощью которой учитывается явление самоиндукции.
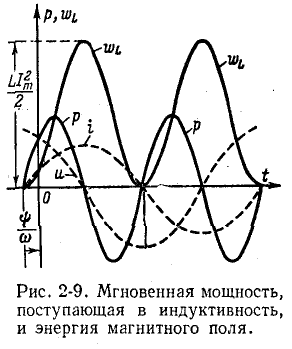
Мгновенная мощность, поступающая в индуктивность, будет:
Она колеблется по синусоидальному закону с угловой частотой 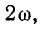
Энергия магнитного поля индуктивности
изменяется периодически с угловой частотой 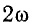
Поступая от источника, энергия временно запасается в магнитном поле индуктивности, затем возвращается в источник при исчезновении магнитного поля. Энергия магнитного поля достигает максимума в момент перехода тока в индуктивности через амплитудное значение, затем она убывает и обращается в нуль при токе, равном нулю.
Таким образом, происходит колебание энергии между источником и индуктивностью, причем активная мощность, поступающая в индуктивность, равна нулю.
Так как максимальная энергия, запасаемая в магнитном поле, равна 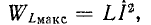

Синусоидальный ток в емкости
Пусть напряжение на емкости С (рис. 2-10, а) синусоидально:
На основании (1-8)
Изменение электрического заряда происходит по синусоидальному закону в соответствии с приложенным напряжением u. При этом попеременное накапливание положительных и отрицательных электрических зарядов на пластинах емкости обусловливает прохождение в цепи синусоидального тока i. Он определяется скоростью изменения заряда на емкости
Выражение (2-11) показывает, что ток i опережает приложенное напряжение и на угол 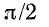
Под фазовым сдвигом тока относительно напряжения здесь, как и раньше, подразумевается разность начальных фаз напряжения и тока, т. е.
Таким образом, в отличие от цепи с индуктивностью, где 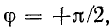
Амплитуды и соответственно действующие напряжение и ток связаны соотношением, подобным закону Ома
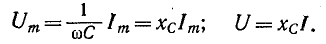
Величина 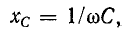
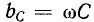
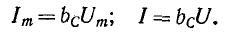
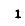
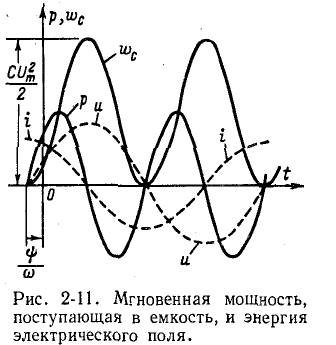
Мгновенная мощность, поступающая в емкость,
колеблется синусоидально с угловой частотой 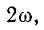
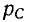
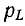
Мгновенная мощность, поступающая в емкость, равна скорости изменения энергии электрического поля емкости.
Энергия электрического поля емкости
изменяется периодически с угловой частотой в пределах от 0 до 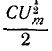
Поступая от источника, энергия временно запасается в электрическом поле емкости, а затем возвращается в источник при исчезновении электрического поля. Энергия электрического поля достигает максимума при амплитудном значении напряжения на емкости. Затем она убывает и обращается в нуль при напряжении, равном нулю.
Таким образом, так же как в случае индуктивности, происходит колебание энергии между источником и емкостью, причем активная мощность Р = 0.
Так как максимальная энергия, запасаемая в электрическом поле, равна Немане 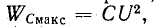
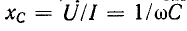
Последовательное соединение
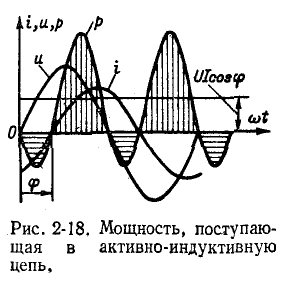
При прохождении синусоидального тока 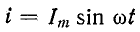
отдельных элементах (второй закон Кирхгофа):
Напряжение 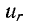
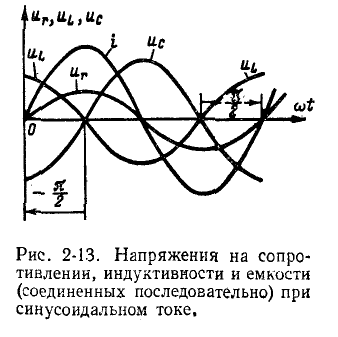
по фазе с током i, напряжение 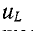
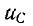
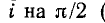
Уравнение (2-12) представляет собой тригонометрическую форму записи второго закона Кирхгофа для мгновенных напряжений. Входящая в него величина х =
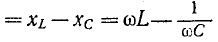
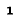
Угол ф отрицателен при емкостном характере цепи, т. е. при х 0) или емкостный (b 0; при этом ток отстает по фазе от напряжения.
Угол 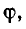
Аналогичная картина получается и в случае активноемкостной цепи
В электрических системах, в которых источниками электрической энергии являются генераторы переменного тока, мощность получается от первичных двигателей, приводящих генераторы во вращение. В радиотехнике и электронике, где синусоидальные колебания создаются с помощью электронных или полупроводниковых приборов, мощность получается от источников постоянного тока, питающих электронные генераторы или другого рода устройства.
Величина, равная произведению действующих тока и напряжения на цепи:
называется полной мощностью цепи и измеряется в вольт-амперах (ва). Следует заметить, что амплитуда синусоидальной составляющей мгновенной мощности (2-25) численно равна полной мощности.
На основании (2-26) и (2-27) коэффициент мощности равен отношению активной мощности к полной:
При расчетах электрических цепей и на практике в эксплуатации пользуются также понятием реактивная мощность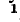
и является мерой потребления (или выработки) реактивного тока.
Эта мощность выражается в единицах, называемых вар.
Выражение реактивной мощности может быть преобразовано с учетом (2-17) и (2-23):
Реактивная мощность может быть также выражена через реактивную составляющую тока 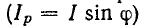
1 Терминами «активная», «реактивная» и «полная» мощности заменены применявшиеся ранее в литературе и ныне не рекомендуемые термины «ваттная», «безваттная» и «кажущаяся» мощности.
В соответствии с принятым ранее правилом знаков для угла 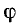
Понятия активная (средняя), реактивная и полная мощности являются удобными определениями мощностей, которые прочно укоренились на практике.
Реактивные мощности, подводимые к индуктивности и емкости, могут быть представлены в следующем виде:
где 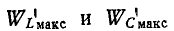
Реактивная мощность цепи, содержащей индуктивность и емкость, пропорциональна разности максимальных значений энергии, запасаемой в магнитном и электрическом полях:
Предлагается читателям проверить и самостоятельно убедиться в том, что эта формула справедлива при любом соединении индуктивности и емкости: последовательном, параллельном или в какой-либо комбинации с сопротивлениями.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Законы и правила Кирхгофа для электрических цепей
- Линии с распределенными параметрами
- Идеализированные пассивные элементы
- Идеализированные активные элементы
- Энергия и мощность электрического тока
- Закон Джоуля — Ленца для тока
- Режимы работы электрических цепей
- Однофазные электрические цепи переменного тока
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Действующее значение переменного токаСкачать

Урок 26. Что такое Фаза и Сдвиг ФазСкачать

Параметры (характеристики)переменного токаСкачать

Математика это не ИсламСкачать

Расчет цепей переменного синусоидального тока | Метод комплексных амплитуд | Часть 3Скачать

6.2 Графическое представление колебаний. Уравнение колебанийСкачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Почему UL опережает iL на 90°│Сдвиг фаз между UL и iL│Катушка в цепи переменного токаСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)