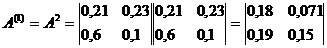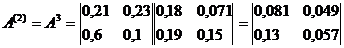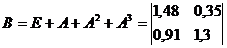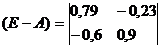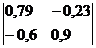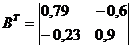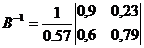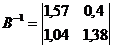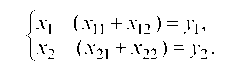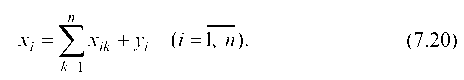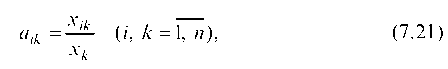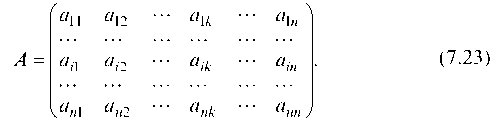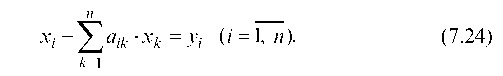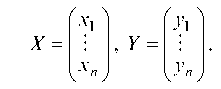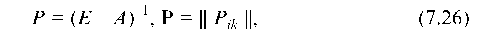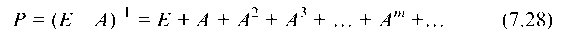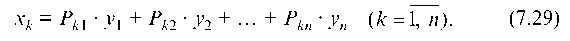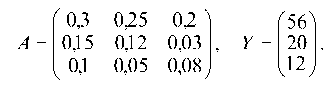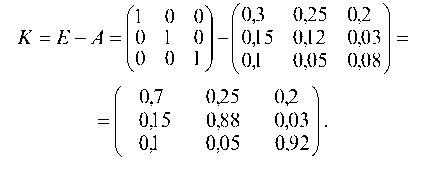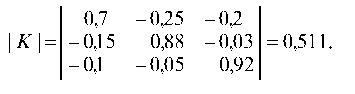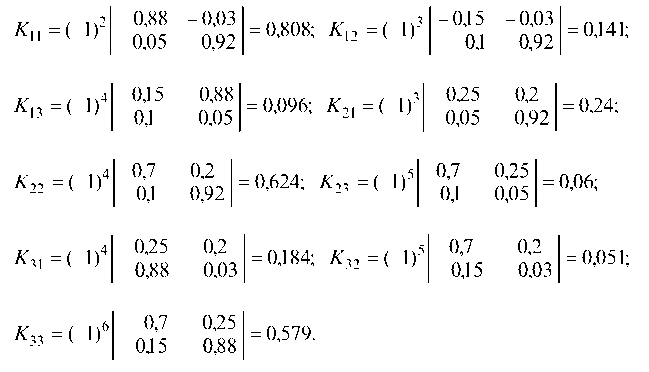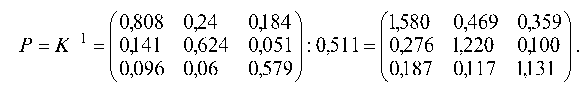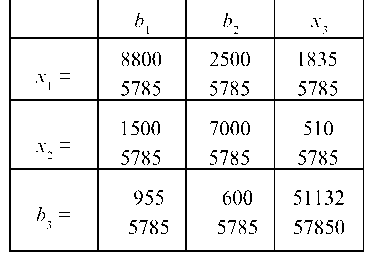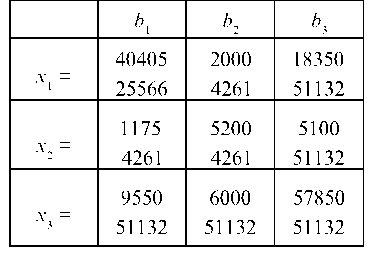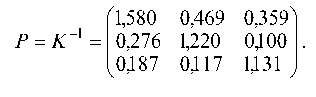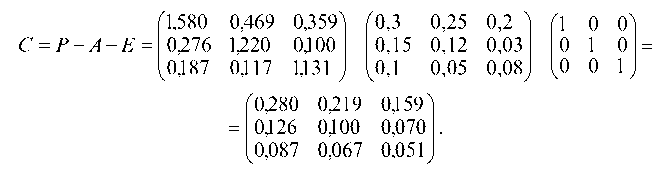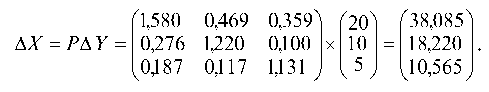Уравнение межотраслевого баланса и его решение (5 видео)

Примеры решений на тему «Межотраслевой баланс»

Отрасль

Потребление

Конечный продукт

Валовой выпуск

Производство

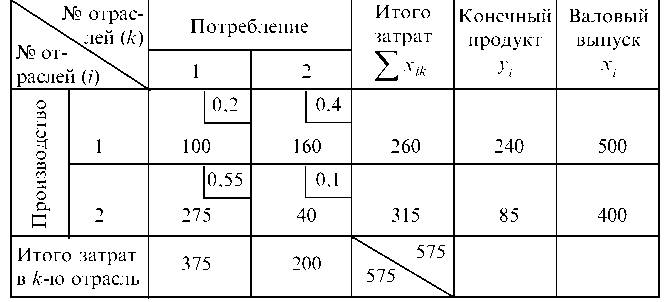
Решение проводим с помощью калькулятора.
По формуле a_ij = x_ij / x_j находим коэффициенты прямых затрат:

0.1

Коэффициент прямых затрат (a_ij) показывает, какое количество продукции i-й отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции j-й отрасли.
Если ввести в рассмотрение матрицу коэффициентов прямых затрат A = (a_ij), вектор-столбец валовой продукции X = (X_i) и вектор-столбец конечной продукции Y = (Y_i), то математическая модель межотраслевого баланса примет вид:
X = AX +Y
Идея сбалансированности лежит в основе всякого рационального функционирования хозяйства. Суть ее в том, что все затраты должны компенсироваться доходами хозяйства. В основе создания балансовых моделей лежит балансовый метод – взаимное сопоставление имеющихся ресурсов и потребностей в них.
Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
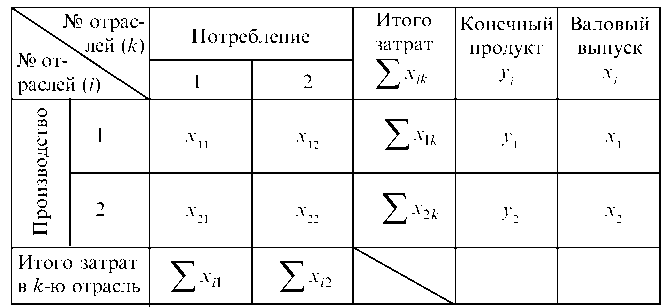
Пусть экономика страны имеет n отраслей материального производства. Каждая отрасль выпускает некоторый продукт, часть которого потребляется другими отраслями (промежуточный продукт), а другая часть – идет на конечное потребление и накопление (конечный продукт).
Обозначим через X_i (i=1..n) валовый продукт i-й отрасли; x_ij – стоимость продукта, произведенного в i-й отрасли и потребленного в j-й отрасли для изготовления продукции стоимостью X_j; Y_i – конечный продукт i-й отрасли.
Критерии продуктивности матрицы А
Существует несколько критериев продуктивности матрицы А.
1. Матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.
2. Для того чтобы обеспечить положительный конечный выпуск по всем отраслям необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
3. Определитель матрицы (E — A) не равен нулю, т.е. матрица (E- A) имеет обратную матрицу (E — A) -1 .
4. Наибольшее по модулю собственное значение матрицы А, т.е. решение уравнения |λE — A| = 0 строго меньше единицы.
5. Все главные миноры матрицы (E — A) порядка от 1 до n, положительны.

Матрица A имеет неотрицательные элементы и удовлетворяет критерию продуктивности (при любом j сумма элементов столбца ∑a_ij ≤ 1.
I. Определим матрицу коэффициентов полных материальных затрат приближенно, учитывая косвенные затраты до 2-го порядка включительно.
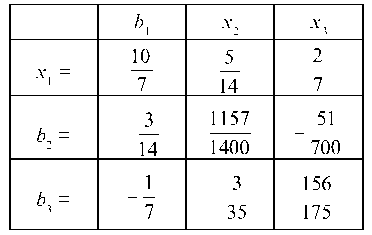
а) Матрица коэффициентов косвенных затрат 1-го порядка равна:

б) Матрица коэффициентов косвенных затрат 2-го порядка равна:

Матрица коэффициентов полных затрат приближенно равна:

II. Определим матрицу коэффициентов полных затрат точно с помощью формул обращения невырожденных матриц.
Коэффициент полных затрат (b_ij) показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.
Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.
а) Находим матрицу (E-A):

б) Вычисляем обратную матрицу (E-A) -1 :
Запишем матрицу в виде:

Главный определить
∆ = (0.79 • 0.9-(-0.6 • (-0.23))) = 0.57234043753495
Транспонированная матрица

Обратная матрица

Найдем величины валовой продукции двух отраслей

Для определения элементов первого квадранта материального межотраслевого баланса воспользуемся формулой x_ij = a_ij • X_j.
Составляющие третьего квадранта (условно-чистая продукция) находятся как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.
Межотраслевой баланс состоит из четырех квадрантов (табл.). Первый квадрант отражает межотраслевые потоки продукции. Второй характеризует отраслевую материальную структуру национального дохода.
Третий представляет национальный доход как стоимость условно-чистой продукции (Z_j), равной сумме амортизации (c_j), оплаты труда (v_j) и чистого дохода j-й отрасли (m_j). Четвертый квадрант показывает конечное распределение и использование национального дохода.

Чистый доход

Валовый продукт

Содержание

Примеры заданий
7.2.2. Межотраслевой баланс
Примеры решений задач по межотраслевому балансу
Бесплатные примеры: межотраслевой баланс (МОБ)
📽️ Видео

Видео:Модель Леонтьева. Теория и решение задачи.Скачать

Примеры заданий

1. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y. Найти вектор валовой продукции, составить межотраслевой баланс.
Пример №1, Пример №2, Пример №3, Пример №4, Пример №5, Пример №6, Пример №7, Пример №8, Пример №9, Пример №10, Пример №11

2. Рассматривается двухотраслевая модель экономики. Даны матрица прямых затрат A и вектор конечной продукции Y. Найти следующее:

Проверить продуктивность матрицы A;
Вектор валового выпуска;
Межотраслевые поставки;
Записать схему межотраслевого баланса.

Скачать решение

3. В отчетном периоде имел место следующий баланс продукции (тыс. тонн). Рассчитайте коэффициенты прямых затрат, полных затрат и косвенных затрат первого порядка. Сделайте запись баланса в матричной форме.
Решение.

4. В отчетном году натуральный баланс продукции выглядел следующим образом ( в тыс. тонн). На основе данного баланса:

Составьте матрицу прямых затрат.
Составьте матрицу полных затрат.
Рассчитайте коэффициенты косвенных затрат первого и второго порядка.
Запишите баланс в матричной форме.
Рассчитайте объем валовой продукции, если конечное потребление составит: Y(140,120,280).

Скачать решение.

5. Два цеха предприятия выпускают продукцию двух видов: цех № 1 – продукцию В, цех № 2 – продукцию С. Часть производимой продукции направляется на внутреннее потребление, а остальная является конечным продуктом. Коэффициенты прямых затрат заданы матрицей. Реализация продукции В на сторону составляет по плану 600 тонн, а продукции С – 300 тонн. Составьте плановую модель выпуска продукции (валового и конечного продукта) с учетом внутреннего потребления. Результаты расчетов запишите в таблицу.
Решение.

6. Каждый из трех цехов предприятия выпускает один вид продукции (изделие 1, изделие 2 и изделие 3 соответственно), часть которой направляется на внутрипроизводственное потребление. Коэффициенты прямых затрат и плановые объемы реализации продукции на сторону заданы матрицами. Рассчитайте план выпуска каждого изделия. Результаты расчетов оформите в таблице.
Пример.

7. В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
Решение.

Задание. Пусть экономика условно разделена только на две отрасли, межотраслевой баланс которых с указанием коэффициентов прямых материальных затрат и конечной продукции приведен в таблице. По этим данным рассчитать валовую продукцию каждой отрасли и межотраслевые поставки.
Решение. Скачать решение

Найти максимальный технологический рост и магистраль в динамической модели Леонтьева, задаваемой матрицей затрат
A = (1/2; 1/4
1/16; 1/2)

Видео:Модель межотраслевого баланса. Часть 1 ТеорияСкачать

7.2.2. Межотраслевой баланс

7.2.2.1. Модель межотраслевого баланса

Балансовый метод применяется для анализа, нормирования, прогноза и планирования производства и распределения продукции на различных уровнях — от отдельного предприятия до народного хозяйства в целом.

Центральная идея межотраслевого баланса (МОБ) заключается в том, что каждая отрасль в нем рассматривается и как производитель, и как потребитель. Модель МОБ — одна из самых простых экономико-математических моделей. Она представляет собой единую взаимосвязанную систему информации о взаимных поставках продукции между всеми отраслями производства, а также об объеме и отраслевой структуре основных производственных фондов, обеспеченности народного хозяйства ресурсами труда и т. д.

Такая модель позволяет рассчитать сбалансированный план на основе точного учета всех межотраслевых связей и рассмот-

реть при этом множество возможных вариантов. В основе исследований балансовых моделей лежат балансовые таблицы, содержащие данные о производстве и потреблении продукции различных отраслей или предприятий. Характерные черты и особенности этого метода описываются с помощью матричных моделей баланса. Из математических методов здесь главным образом используется аппарат линейной алгебры.

Рассмотрим пример предельно упрощенной системы, состоящей из двух производственных отраслей. Пусть исполнение баланса за предшествующий период характеризуется данными, приведенными в табл. 7.15.

Продукция каждой отрасли частично идет на внешнее потребление (конечный продукт), а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции (1-й столбец продукции) и как ее потребитель (1-я строка таблицы). Приведенную таблицу конкретного примера можно записать и в более общем виде (табл. 7.16).

Обозначим через хг валовый выпуск продукции г-й отрасли за планируемый период и через у — конечный продукт, идущий на внешнее для рассматриваемой системы потребление (средства производства других экономических систем, потребление населения, образование запасов и т. д.). Таким образом, разность (хг — ^г) составляет часть продукции i-й отрасли, предназначенную для внутрипроизводственного потребления. Предполагаем, что баланс составляется в стоимостном разрезе. Обозначим через xik часть продукции i-й отрасли, которая потребляется k-й отраслью, для обеспечения выпуска ее продукции в размере xi.

Очевидно, величины, расположенные в строках, связаны следующими балансовыми равенствами:

Отсюда стоимостной баланс в общем виде запишется уравнениями:

Рассмотрев отношение количества продукции i-й отрасли, поступающей в k-ю отрасль для обеспечения выпуска ее продукции в размере xk, получим затраты на единицу валовой продукции

Рассчитываем агк по формуле (7.21) и записываем в табл. 7.15 в углах соответствующих клеток.

Найденные коэффициенты прямых затрат и образуют неотрицательную матрицу прямых затрат:

Подставляя в уравнение (7.20) соотношения (7.22) получим:

Систему уравнений МОБ (7.24) запишем в матричной форме

где Е — единичная матрица, А — матрица прямых затрат (7.23), X и Г — столбцовые матрицы

7.2.2.2. Полные внутрипроизводственные затраты

Р = (Е — А)-1, Р = || Р1к ||, (7.26)

тогда из (7.25): (Е — А)-1 ¦ (Е — А) ¦ X = (Е — А)-1 ¦ Г и, так как

(Е — А) ¦ (Е — А) = Е и ЕХ = X, то получаем, что объемы произ-

водства отраслей X определяются как

по заданным величинам конечного продукта потребления Г и матрице Р, которую называют матрицей коэффициентов полных затрат.

Элементы матрицы Р включают не только затраты i-й продукции, необходимой для создания одной единицы k-й продукции, но и те затраты, которые необходимы для создания в каждой отрасли одной единицы конечного продукта.

7.2.2.3. Косвенные затраты

Значит полные затраты Pik включают как прямые aik так и косвенные (Pik — aik) затраты. Очевидно, что всегда Pik > aik, точнее

Матрицы А2, А3, . , Ат. называются матрицами коэффициентов косвенных затрат 1-го, 2-го и т. д. порядков и коэффициенты полных затрат получают в виде суммы коэффициентов прямых затрат и косвенных затрат.

Прямые затраты не отражают в полной мере сложных количественных взаимосвязей, наблюдающихся в народном хозяйстве. Они в частности не отражают обратных связей, имеющих далеко не маловажное значение.

Как возникают косвенные затраты? Например, на изготовление трактора в виде прямых затрат расходуется чугун, сталь, и т. д., но для производства стали также нужен чугун. Таким образом, кроме прямых затрат чугуна, имеются и косвенные затраты чугуна, связанные с производством трактора. В эти косвенные затраты входит и чугун, необходимый для создания того количества чугуна, которое составляет прямые затраты. Эти косвенные затраты могут иногда существенно превышать прямые затраты.

Исходя из (7.27), валовый выпуск k-й отрасли хк определяется как

Модель межотраслевого баланса (7.24), (7.25) или (7.29) позволяет решить следующие задачи:

1) определить объем конечной продукции отраслей y1, y2, ., yn по заданным объемам валовой продукции х1, х2, . хп;

2) по заданной матрице коэффициентов прямых затрат А определить матрицу коэффициентов полных затрат P, элементы которой служат важными показателями для планирования развития отраслей;

3) определить объем валовой продукции отраслей хь х2, ., хп по заданным объемам конечной продукции у1, у2, . уп.

4) по п заданным объемам конечной или валовой продукции отраслей х1, .у2, х3, .у4, . определить оставшиеся п объемов.

7.2.2.4. Решение типовой задачи

Рассмотрим пример составления межотраслевого баланса производства и распределения продукции для трехотраслевой экономической системы, заданной матрицей коэффициентов прямых затрат А и вектором конечной продукции Г:

Найти коэффициенты полных затрат: плановые объемы валовой продукции X = (х1; х2, Х3); величину межотраслевых потоков, т. е. значения хгк (г = 1, 2, 3; к = 1, 2, 3); матрицу косвенных затрат; по заданному вектору увеличения косвенного выпуска продукции ДГ определить изменение плана ДХ.

Находим матрицу (Е — А):

Для определения матрицы полных затрат (7.28) обращаем матрицу К.

Первый способ нахождения К 1 = (Е — А)-1. Вычисляем определитель

Так как | К | ф 0, то существует матрица К 1 = Р обратная заданной матрице К.

Находим алгебраические дополнения для элементов матрицы К.

Из алгебраических дополнений составляем транспонированную матрицу и, деля ее на | К |, получаем обратную матрицу К -1:

Рассмотрим другой способ нахождения обратной матрицы К 1 с помощью жордановых исключений. Составляем табл. 7.17.

Совершаем последовательно три шага жордановых исключений, меняя местами Ьг — и х., получаем табл. 7.18—7.20.

Внутри табл. 7.20 стоит обратная матрица K 1. Округляя до третьего знака после запятой, имеем:

(1,580 0,469 0,359^	( 56 ^	(102,197^
X = PY =	0,276 1,220 0,100	20	=	41,047
0Д87 0,117 1Д31 0	I12 0	26,383

Следовательно, плановые объемы валовой продукции трех отраслей, необходимые для обеспечения заданного уровня конечной продукции равны:

х1 = 102,2; х2 = 41,0; х3 = 26,4.

Для составления баланса рассчитываем межотраслевые потоки средств производства по формуле (7.22):

x11 = 0,3 • 102,2 = 37,7; x21 = 0,15 • 102,2 = 15,3; x31 = 0,1 • 102,2 = 10,2; x12 = 0,25 • 41,0 = 10,2; x22 = 0,12 • 41,0 = 4,9; x32 = 0,05 • 41,0 = 2,1; x13 = 0,2 • 26,4 = 5,3; x23 = 0,03 • 26,4 = 0,8; x33 = 0,08 • 26,4 = 2,1.

Результаты вычислений представим в форме межотраслевого баланса (табл. 7.21). Величина чистой продукции определяется здесь как разница между валовой продукцией отрасли и суммой межотраслевых потоков в каждом столбце.

^^^Потребляющие отрасли Произво-^^^^ дящие отрасли^^	1	2	3	Конечная	Валовая
1	30,7	10,2	5,3	56	102,2
2	15,3	4,9	0,8	20	41,0
3	10,2	2,1	2,1	12	26,4
Чистая продукция	46,0	23,8	18,2	—	—
Валовая продукция	102,2	41,0	26,4	—	169,6

На основе заданных матриц Y и A по уровню конечного продукта и коэффициентов прямых затрат получен полностью сбалансированный план общего производства продукции и ее рас-

пределения как между отраслями в качестве средств производства, так и для конечного использования.

Матрицу косвенных затрат найдем из формулы (7.28):

Определяем изменение плана ДХ, которое потребуется при увеличении конечного выпуска продукции 1-й отрасли на 20, 2-й — на 10 и 3-й — на 5 (единиц).

Следовательно, потребуется увеличить валовый выпуск 1-й отрасли на Дх1 = 38,1, 2-й отрасли на Дх2 = 18,2 и 3-й отрасли на 10,6 (единиц).

Видео:Модель межотраслевого баланса. Часть 2 ПрактикаСкачать

Примеры решений задач по межотраслевому балансу

Модель межотраслевого баланса, или метод затраты-выпуск (или позднее модель Леонтьева), разработана выходцем из России, американцем В.В. Леонтьевым. В 30-е годы XX века метод был продемонстрирован на практике на примере экономики США и затем получил широкое применение для анализа и прогноза взаимодействия экономик отраслей, стран и континентов.

При изучении математических методов экономики студенты изучают классическую модель затраты-выпуск, которая является линейной и статической и обычно решается матричными методами линейной алгебры. Приведем несколько примеров решений задач с межотраслевыми моделями.

Вы можете заказать решение своей работы по межотраслевому балансу в МатБюро: Решение задач по экономико-математическим методам.

Видео:Экономист Леонтьев - Уравнение межотраслевого баланса - Возможность решения уравнения (§ 17.101)Скачать

Бесплатные примеры: межотраслевой баланс (МОБ)

Задача 1. В таблице приведены коэффициенты прямых затрат и конечная продукция отраслей на плановый период, усл. ден.ед.(таблица в файле)
Найти:
1. плановые объемы валовой продукции отраслей, межотраслевые поставки, чистую продукцию отраслей;
2. необходимый объем валового выпуска каждой отрасли, если конечное потребление продукции сельского хозяйства увеличится на k%, а промышленности на l%.

Задача 2. Задание:
— построить таблицу межотраслевого баланса в стоимостном выражении;
— найти изменения валовых выпусков при увеличении конечного выпуска первой отрасли на 20%, третьей на 10% и неизменном конечном выпуске второй отрасли;
— как следует изменить цены на продукцию отраслей, если поставлены задачи увеличения добавленной стоимости в первой отрасли на 20%, а в третьей на 10%.
Дана матрица А коэффициентов прямых материальных затрат с компонентами (aij) и вектор конечного выпуска у с компонентами (yi).
а11 а12 а13 а21 а22 а23 а31 а32 а33 у1 у2 у3
0,3 0,4 0,1 0,2 0,2 0,1 0,3 0,2 0,1 100 150 190

Задача 3. Самостоятельно придумать какую-нибудь линейную модель равновесных цен размера 3х3 и решить её. Затем увеличить на 10 % норму добавленной стоимости в какой-нибудь одной отрасли и вычислить новый вектор равновесных цен, сравнить (в %) со старым.

Задача 4. Дан следующий отчетный межотраслевой баланс (МОБ) (таблица в файле)
Здесь в шахматке указаны межотраслевые потоки промежуточной продукции, в последних двух строках (за пределами таблицы) – объемы затрат труда и фондов, а в последнем столбце – конечная продукция.
Задания для выполнения работы
1. Построить таблицу отчетного МОБ, проверить основное балансовое соотношение.
2. Составить плановый МОБ при условии увеличения спроса на конечный продукт по отраслям соответственно на 10, 9, 7, 8 и 7 процентов.
3. Рассчитать коэффициенты прямых и полных затрат труда и фондов и плановую потребность в соответствующих ресурсах.
4. Проследить эффект матричного мультипликатора при дополнительном увеличении конечного продукта по 3-ей отрасли на 5 %.
5. Рассчитать равновесные цены при увеличении зарплаты по всем отраслям на 10 % (считать доли зарплаты в добавленной стоимости по отраслям следующими: 0,33, 0,5, 0,35, 0,43, 0,6). Проследить эффект ценового мультипликатора при дополнительном увеличении зарплаты в 1-й отрасли на 5 %.

Задача 5. Придумать свою какую-нибудь продуктивную матрицу размера 2х2 и вычислить запас продуктивности двумя способами.