Уравнение между прямой и плоскостью онлайн (6 видео)

Угол между прямой и плоскостью онлайн

С помощью этого онлайн калькулятора можно найти угол между прямой и плоскостью. Дается подробное решение с пояснениями. Для вычисления угла между прямой и плоскостью введите элементы уравнения и плоскости в ячейки и нажимайте на кнопку «Решить». Теоретическую часть смотрите ниже.

Содержание

Предупреждение
Угол между прямой и плоскостью − теория, примеры и решения
Онлайн калькулятор. Угол между прямой и плоскостью.
Найти угол между прямой и плоскостью
Ввод данных в калькулятор для вычисления угла между прямой и плоскостью
Дополнительные возможности калькулятора вычисления угла между прямой и плоскостью
Теория. Угол между прямой и плоскостью
Решение задач по математике онлайн
Калькулятор онлайн. Вычисление угла между прямой и плоскостью
📸 Видео

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:21. Угол между прямой и плоскостьюСкачать

Угол между прямой и плоскостью − теория, примеры и решения

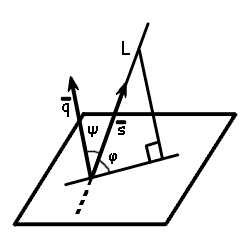
В данной статье мы рассмотрим задачу определения угла φ между прямой L, заданной каноническим уравнением

Уравнение между прямой и плоскостью онлайн

(1)

и плоскостью P, заданной общим уравнением

Ax+By+Cz+D=0.

(2)

где q=(m, l, p) направляющий вектор прямой L, а n=(A, B, C) нормальный вектор плоскости P.

Нормальный вектор плоскости n и направляющий вектор прямой q могут составить острый угол, прямой угол и тупой угол.

Вариант 1. Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q острый (Рис.1):ψ Вариант 2. Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q:ψ=90°. Тогда имеем:

φ=0.

0=cosψ=sinφ.

Вариант 3. Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q тупой (Рис.2):ψ>90°.

cosψ=cos(90+φ)=−sinφ.

(4)

Поскольку угол φ между прямой и плоскостью всегда меньше или равно 90°, то

sinφ=⃒ cosψ ⃒

(5)

Из определения скалярного произведения векторов имеем:

(6)

Из уравнений (5) и (6) можно найти синус угла φ

(7)

(8)

Из формулы (8) можно найти угол между прямой L и плоскостью P.

Пример 1. Найти угол между прямой L:

(9)

(10)

Направляющий вектор прямой L имеет вид q=(m, p, l)=(1, 3, 2). Нормальный вектор плоскости P имеет вид n=(A, B, C)=(2, 6, 1).

Поскольку угол φ между прямой L и плоскостью P является дополнительным к углу ψ между направляющим вектором прямой q=(m,p,l) и нормальным вектором плоскости n=(A,B,C), то cosψ=sinφ. Из определения скалярного произведения (q,n)=|q||n|cosψ. Тогда для угла между прямой L и плоскостью P получим следующую формулу:

(11)

Подставляя значения A, B, C, m, p, l в (11), получим:

Видео:Найти точку пересечения прямой и плоскостиСкачать

Онлайн калькулятор. Угол между прямой и плоскостью.

Предлагаю вам воспользоваться онлайн калькулятором для вычисления угла между прямой и плоскостью.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между прямой и плоскостью и закрепить пройденный материал.

Видео:10 класс, 21 урок, Угол между прямой и плоскостьюСкачать

Найти угол между прямой и плоскостью

Выберите в какой форме задано уравнение прямой:

Ввод данных в калькулятор для вычисления угла между прямой и плоскостью

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления угла между прямой и плоскостью

Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Угол между прямой и плоскостью

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость

Если в пространстве заданы направляющий вектор прямой L

и уравнение плоскости

A x + B y + C z + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	\| A · l + B · m + C · n \|
	√ A 2 + B 2 + C 2 · √ l 2 + m 2 + n 2

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:14. Угол между прямыми в пространствеСкачать

Калькулятор онлайн.
Вычисление угла между прямой и плоскостью

Этот калькулятор онлайн вычисляет угол между прямой и плоскостью.
Плоскость задаётся в виде общего уравнения плоскости:
$$ Ax+By+Cz+D=0 $$

Онлайн калькулятор для вычисления угла между прямой и плоскостью не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac )

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac )