Уравнение методом группировки 7 класс (2 видео)

Разложение многочлена способом группировки

О чем эта статья:

Содержание

Основные понятия
5 способов разложения многочлена на множители
Способ группировки множителей
Способ группировки в более сложных задачах и уравнениях
Конспект урока «Разложение на множители способом группировки» в 7-м классе
📹 Видео

Видео:7 класс, 29 урок, Способ группировкиСкачать

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

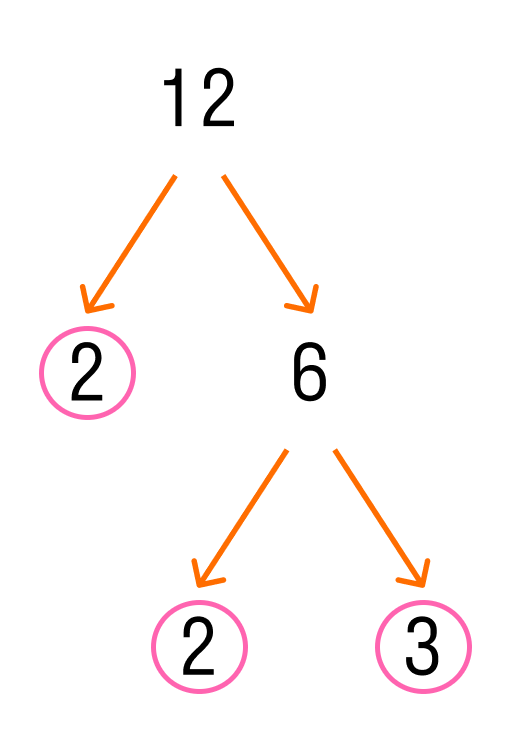
Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые обведены в кружок на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

Видео:Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

5 способов разложения многочлена на множители

Вынесение общего множителя за скобки.
Формулы сокращенного умножения.
Метод группировки.
Выделение полного квадрата.
Разложение квадратного трехчлена на множители.

Видео:Что такое Метод Группировки? Для Чайников, Урок 11Скачать

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
Вынести общий множитель за скобки.
Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И не всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест множителей произведение не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

Найдем общий множитель: (m — n)
Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Видео:Алгебра 7 Разложение многочлена на множители способом группировкиСкачать

Способ группировки в более сложных задачах и уравнениях

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы решим много различных достаточно сложных задач с применением метода группировки. Мы решим много уравнений и научимся геометрически их моделировать.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»

Видео:Разложение многочлена на множители способом группировки. Алгебра, 7 классСкачать

Конспект урока «Разложение на множители способом группировки» в 7-м классе

Разделы: Математика

Цели урока

Образовательные:

повторить и закрепить правило умножения одночлена на многочлен;
повторить и закрепить правило вынесения общего множителя за скобки;
изучить способ разложения на множители с помощью группировки;
закрепить полученные знания с помощью простейших упражнений.

Развивающие:

познакомить учащихся с историческим материалом (фрагменты биографии Эйлера);
использовать полученные знания и умения для решения кроссворда;
применение способа группировки для вычисления числовых выражений и для решения уравнений.

Воспитательные:

развитие внимания и аккуратности;
умение слушать и анализировать выступления одноклассников.

Оборудование

доска, мел, экран;
сканер для проверки домашней работы;
мультимедийный проектор и ноутбук.

Дидактические средства

карточки на печатной основе;
Алгебра: Учебник для 7 кл. ср.шк./ Ю.Н. Макарычев -М.: Просвещение,2005;
Компьютерная презентация, созданная с использованием материалов Фестиваля педагогических идей «Открытый урок» Филимоновой Ирины Владимировны.

Тип урока: объяснение и закрепление нового материала (первый урок по данной теме).

Ход урока

I. Оргмомент

Проверьте, все ли приготовили к уроку: учебник, тетрадь, письменные принадлежности, дневник.

Запишите новое домашнее задание: № 757, № 763, № 769, п. 29.

II. Проверка домашнего задания

На доске записать решение № 738(б, в) и № 781(а) — 2 ученика;

В это время с помощью проектора проверяем заранее отсканированные № 738(а, г) и № 743.

Вопросы отвечающим: что такое одночлен, что называется многочленом, как умножить одночлен на многочлен, как умножить многочлен на многочлен.

III. Объяснение нового материала

Что мы сделали в последнем действии № 743? (Разложили на множители)

Что для этого сделали? (Вынесли общий множитель за скобки)

Этот множитель может быть любым. (Работа с ЗЕЛЕНОЙ карточкой)

18а +ха = а(18+х)
18 (а+b) + x (а+b) = (а+b) (18+x)

Сравните знакомый слайд с новым:

Для разложения на множители мы сгруппировали по два одночлена и вынесли в каждой группировке общий множитель за скобки.

Потренируемся на примерах. (Учитель пишет на доске)

x(b+c)+ 3b+3c
mx+my+6x+6y
xy+2y — 2x — 4

IV. Первичное закрепление

Решение № 755(б, в), № 756(б, в) на доске (по очереди выходят решать 4 ученика)

y(a-c)+5a — 5c
p(c- d)+q — p
9x+ay+9y+ax
7a — 7b + an — bn

V. Исторический экскурс (Презентация)

Известный математик (1707 — 1783 гг.) родился в Швейцарии. В 1727 г. двадцатилетним юношей он был приглашен в Петербургскую Академию наук. Этот математик был соратником Ломоносова. В Петербурге он попадает в круг выдающихся ученых математиков, физиков, астрономов, получает широкую возможность для создания и издания своих трудов (их у него было более 800, и заняли они 72 тома). Среди его работ — первые учебники по решению уравнений. Старшеклассники учатся по учебникам, прообразы которых создал этот ученый. Его считают великим учителем математики. Последние в научном мире он работал слепым, но продолжал работать, диктовал труды своим ученикам. Однако в научном мире он больше известен как физик, который построил точную теорию движения луны с учетом притяжения не только Земли, но и Солнца.

Фамилию этого ученого вы узнаете, если правильно решите следующие пять заданий : разложите на множители способом группировки (Ученики решают эти задания, находят буквы в таблице результатов. Читают слово: Эйлер).

Устали? Вот интересное задание. Расшифруйте ребус.

VI. А теперь применим способ группировки для вычисления числовых выражений.

Не забудьте поставить себе оценку в оценочный лист.

VII. (Второй урок) Закрепление полученных знаний.

Решение №758 и 761 на доске с подробными комментариями.

VIII. Решение текстовой задачи на повторение.

Число коров в стаде	Удой от 1 коровы	Удой от стада
Было	х	12,8 л	12,8 х л
Стало	х+60	15 л	15 (х+60) л

По условию задачи известно, что удой от стада увеличился на 1340 л, поэтому составляем уравнение:

15(х+60) — 12,8 х = 1340;

15х +900 — 12,8х = 1340;

Тогда 200+60 = 260 (коров)

Ответ: в стаде стало 260 коров.

Оцените себя:

правильно составлено математическая модель задачи — 2 балла;
правильно составлено уравнение — 1 балл;
правильно решено уравнение — 2 балла;
выполнено следующее действие после уравнения — 1 балл.

IX. Подведение итогов.

Что сегодня на уроке мы повторили?
Что вы для себя усвоили?
Чему научились?
Отметьте в оценочной карточке ваше отношение к уроку:
- Я доволен уроком, мне очень понравилось.
- Мне понравилось на уроке, но в моих знаниях есть пробелы.
- Урок прошел для меня даром, ни чего нового я на нем не узнал. Все, это я знаю.
- Я не доволен уроком, ничего не понял и как решать примеры я не знаю.