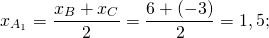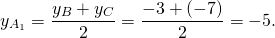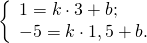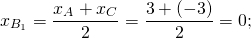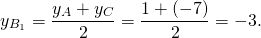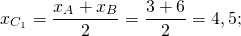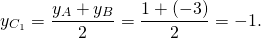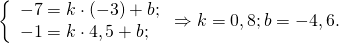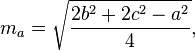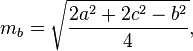Уравнение меридианы треугольника по координатам

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

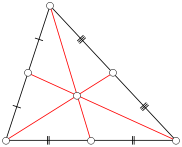
A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать Длина медианы треугольника Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок. Каждый треугольник имеет ровно три медианы, по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. В случае равнобедренного и равностороннего треугольников, медиана делит пополам любой угол в вершине у которого две смежные стороны равны. Видео:Уравнения стороны треугольника и медианыСкачать Калькулятор длины медианы треугольника Онлайн калькулятор расчета длины медианы треугольника при условии, что известны координаты его вершин. Нахождение длины трех медиан треугольника Формула расчета длины медианы a,b,c — Длина сторон треугольника. Пример расчета медиан: Даны точки A( 1 , 5 ), B( 8 , 9 ) и C( 5 , 6 ). Найдите медианы треугольника. Получаем: A( 1 , 5 ) B( 8 , 9 ) C( 5 , 6 ) Решение: Шаг 1: Найдем длину сторон a,b,c используя формулу Найдем длину стороны A между точками B( 8 , 9 ) and C( 5 , 6 ) a = √((5 — 8) 2 + (6 — 9) 2 )= 4.242 Найдем длину стороны B между точками C( 5 , 6 ) и A( 1 , 5 ) b = √((1 — 5) 2 + (5 — 6) 2) = 4.123 Найдем длину стороны C между точками A( 1 , 5 ) и B( 8 , 9 ) c = √((8 — 1) 2 + (9 — 5) 2) = 8.062 Шаг 2: Полученные значения a,b,c применяем в формулы ma = (1/2) √2c 2 + 2b 2 — a 2 mb = (1/2) √(2c 2 + 2a 2 — b 2 ) mc = (1/2) √(2a 2 + 2b 2 — c 2 ) ma = (1/2)√(2(8.062) 2 + 2(4.123) 2 — 4.242 2 )= 6.042 mb = (1/2)√(2(8.062) 2 + 2(4.242) 2 — 4.123 2 )= 6.103 mc = (1/2)√2(4.242) 2 + 2(4.123) 2 — 8.062 2 = 1.118 💥 Видео Уравнение медианыСкачать №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать Длина медианы треугольникаСкачать Вычисление медианы, высоты и угла по координатам вершинСкачать Уравнение прямой и треугольник. Задача про медиануСкачать Вычисляем высоту через координаты вершин 1Скачать Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать найти уравнение высоты треугольникаСкачать Уравнения прямой на плоскости | Векторная алгебраСкачать Уравнение прямой и треугольник. Задача про высотуСкачать Аналитическая геометрия на плоскости. Решение задачСкачать найти уравнения биссектрис углов между прямымиСкачать Аналитическая геометрия, 6 урок, Уравнение прямойСкачать Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать Даны координаты вершин треугольника АВС.Скачать Вычисляем угол через координаты вершинСкачать Формулы для медианы треугольникаСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства