В основе молекулярной физике лежит ряд эмпирических (опытных) законов. Данные законы основаны на многолетних наблюдениях и особого вывода для них нет. До введения самих законов, познакомимся с понятием состояния идеального газа. Так, под состоянием идеального газа понимается совокупность термодинамических параметров, характеризующих газ в данный момент:
- — давление газа,
- — объём газа,
- — температура газа,
- — масса газа.
Если данные параметры изменяются, мы будем говорить об изменении состоянии идеального газа.
- закон Авогадро
Закон Авогадро гласит, что для любых газов, взятых при одинаковых давлениях и температурах, содержится одинаковое количество молекул. Также есть несколько следствий из этого закона: одинаковое количество молей разных газов при одинаковых условиях (давление и температура), занимают одинаковый объём (молярный объём). Для нас главный вывод данного закона состоит в том, что для любого газа, химическое количество которого равен 1 моль, количество молекул в нём равно штук — постоянная Авогадро.
- закон Бойля — Мариотта
Закон Бойля -Мариотта гласит, что при условии постоянства массы (химического количества) и температуры газа, произведение давления газа на его объём постоянно:
Альтернативная форма записи:
- где
- , — давление газа в первом и втором состоянии соответственно,
- , — объём газа в первом и втором состоянии соответственно.
Таким образом, при наших условиях, уравнение (2) связывает два любых состояния идеального газа.
- закон Гей — Люссака
Закон Гей — Люссака гласит, что при условии постоянства массы (химического количества) и давления газа, отношение объёма газа к его температуре постоянно:
Альтернативная форма записи:
- где
- , — объём газа в первом и втором состоянии соответственно,
- , — температура газа в первом и втором состоянии соответственно.
Таким образом, при наших условиях, уравнение (4) связывает два любых состояния идеального газа.
Закон Шарля гласит, что при условии постоянства массы (химического количества) и объёма газа, отношение давления газа к его температуре постоянно:
Альтернативная форма записи:
- где
- , — давление газа в первом и втором состоянии соответственно,
- , — температура газа в первом и втором состоянии соответственно.
Таким образом, при наших условиях, уравнение (6) связывает два любых состояния идеального газа.
- закон Дальтона
Закон Дальтона несколько выбивается из логики предыдущих опытных законов, т.к. он описывает не отдельный газ, а составной (так называемую смесь газов). Итак, для смеси газов: суммарное давление смеси газов равно сумме парциальных давлений каждого из его компонентов:
- где
- — давление смеси газов,
- — парциальные (одиночные) давления каждого из газов в отдельности.
На основании введённых опытных законов можно получить общее соотношение, совмещающее все параметры, характеризующие газ (уравнение Менделеева-Клапейрона):
- где
- — давление газа,
- — объём газа,
- — химическое количество газа,
- — температура газа,
- м *кг*с *К *Моль — газовая постоянная.
Соотношение (8), оно же уравнение Менделеева-Клапейрона, одно из самых важных во всём курсе термодинамики и молекулярной физики. Исходя из этого соотношения, можно получить все газовые законы (1), (3), (5).
Вывод: для большинства задач молекулярной физики газ переводят из одного состояния во второе (может и дальше), каждое из этих состояний можно описать соотношением (8), а потом, разрешив получившуюся систему уравнений, найти ответ.
Вывод: соотношения (1) — (6) несомненно убыстряют решение задачи, однако уравнение (8) срабатывает в любом случае (предлагаю использовать только его).
Вывод: единственным общим соотношением для смеси газов является соотношение (7).
- Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Объединенный газовый закон и изопроцессы
- теория по физике 🧲 молекулярная физика, МКТ, газовые законы
- Объединенный газовый закон применительно к изопроцессам
- Изотермический процесс. Закон Бойля — Мариотта.
- Изохорный процесс. Закон Шарля.
- Изобарный процесс. Закон Гей-Люссака.
- Графики изопроцессов
- 🎥 Видео
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 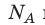
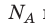
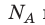
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
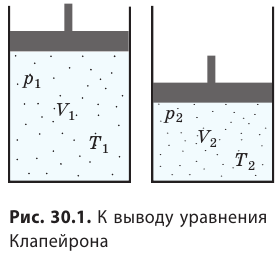
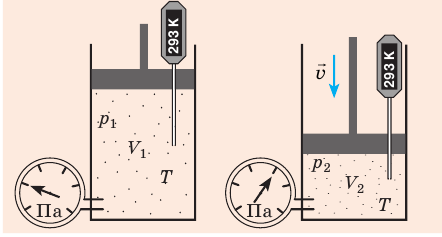
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (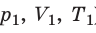
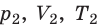
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 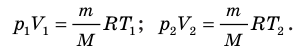
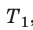
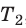
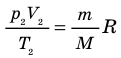
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (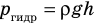
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (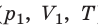
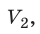
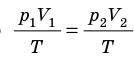
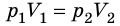
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
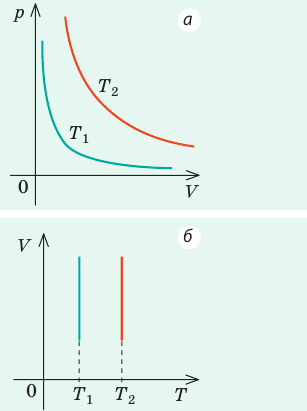
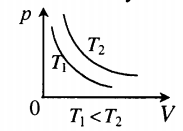
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 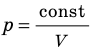
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (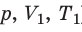
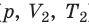
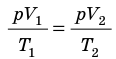
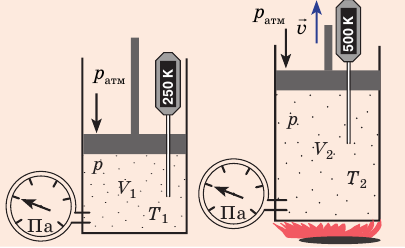
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
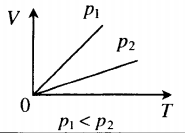
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (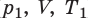
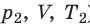
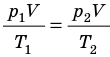
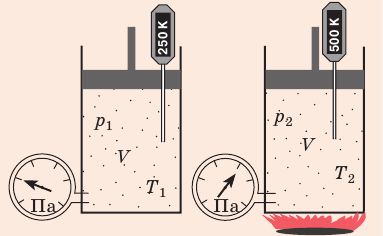
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
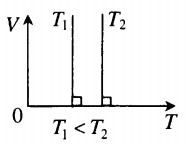
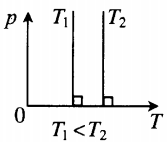
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
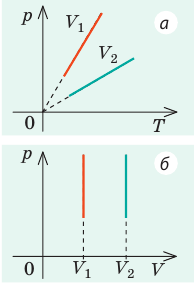
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 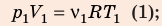
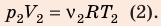

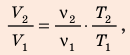
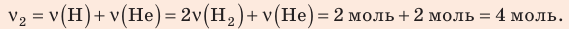
Ответ: примерно в 2,7 раза.
Пример №2
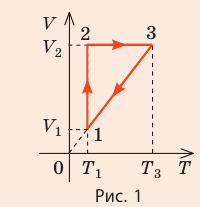
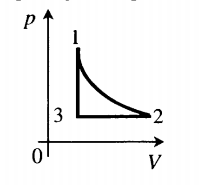
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
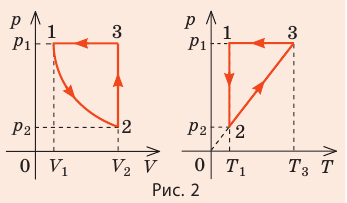
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Объединенный газовый закон и изопроцессы
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:
При постоянной массе газа и его неизменной молярной массе отношение произведения давления на объем к его абсолютной температуре остается величиной постоянной:
p V T . . = c o n s t и л и p 1 V 1 T 1 . . = p 2 V 2 T 2 .
Видео:62. Уравнение Клапейрона-МенделееваСкачать

Объединенный газовый закон применительно к изопроцессам
Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.
Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным.
Изотермический процесс. Закон Бойля — Мариотта.
Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:
Для изотермического процесса действует закон Бойля — Мариотта:
Закон Бойля — Мариотта
Для газа данной массы произведение газа на его объем постоянно, если температура газа не меняется.
Изохорный процесс. Закон Шарля.
Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:
Для изохорного процесса действует закон Шарля:
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
p T . . = c o n s t ( p 1 T 1 . . = p 2 T 2 . . )
Изобарный процесс. Закон Гей-Люссака.
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
V T . . = c o n s t ( V 1 T 1 . . = V 2 T 2 . . )
Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.
Так как газ нагревают, то:
Запишем закон Шарля применительно к данному случаю:
p T 1 . . = 1 , 6 p 240 + T 1 . .
Сделаем некоторые преобразования и вычислим начальную температуру:
p T 1 . . = 1 , 6 p 240 + T 1 . .
240 + T 1 = 1 , 6 T 1
T 1 = 240 0 , 6 . . = 400 ( К )
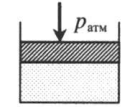
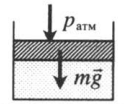
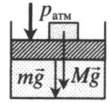
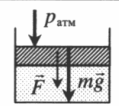
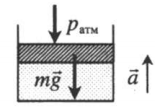
Подсказки к задачам на газовые законы
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
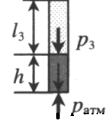 | |||||||||||||||||
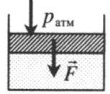
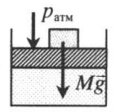
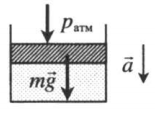
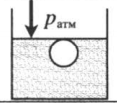
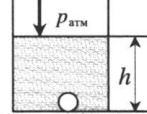
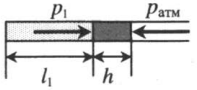
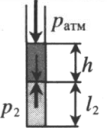
| Шар или понтон поднимается вверх в воздухе или жидкости | Архимедова сила больше силы тяжести: Пример №2. Поршень площадью 10 см 2 массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с 2 ? Изменение температуры газа не учитывать. 10 см 2 = 10 –3 м 2 100 кПа = 10 5 Па Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем: p 1 = p а т м + m g S . . Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх: p 2 = p а т м + m g S . . + m a S . . Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно: Объемы в 1 и 2 случае будут определяться формулами: h1 — расстояние от нижнего края поршня до дна сосуда в первом случае. h2 — та же самая величина, но во втором случае (искомая величина). Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов: p 1 V 1 = S h 1 ( p а т м + m g S . . ) p 2 V 2 = S h 2 ( p а т м + m g S . . + m a S . . ) Так как это изотермический процесс, правые части уравнений можно приравнять: S h 1 ( p а т м + m g S . . ) = S h 2 ( p а т м + m g S . . + m a S . . ) Видео:Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать  Видео:Основы молекулярной физики | закон Гей - ЛюссакаСкачать  Графики изопроцессовИзопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.
|
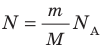
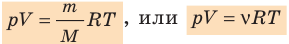
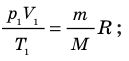
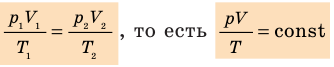
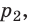
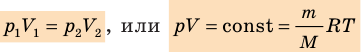

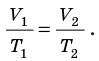
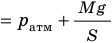
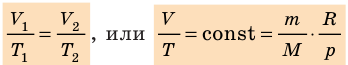
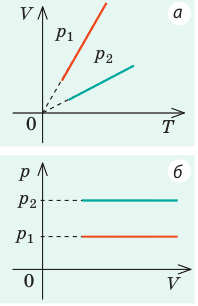

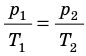
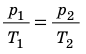
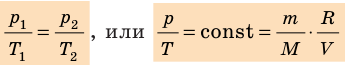

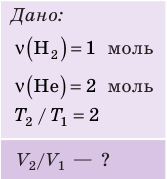
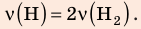

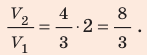
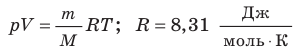 — универсальная газовая постоянная.
— универсальная газовая постоянная.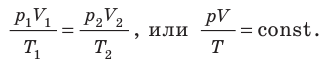

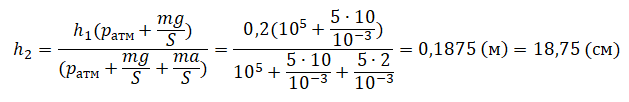
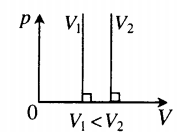
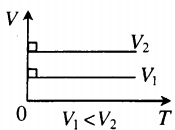
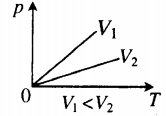
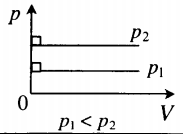

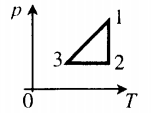
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.












