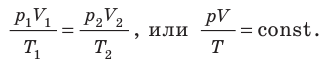| Название | Уравнение КлапейронаМенделеева. Основное уравнение молекулярнокинетической теории идеальных газов |
| Анкор | Уравнение Клапейрона-Менделеева реферат |
| Дата | 24.11.2021 |
| Размер | 38.37 Kb. |
| Формат файла |  |
| Имя файла | Уравнение Клапейрона-Менделеева реферат.docx |
| Тип | Реферат #280997 |
| Подборка по базе: Дифференциальное уравнение высших порядков.docx, Английский язык. Основное общее образование.docx, Курсоая работа на тему Основное содержание позитивной ответствен, ОКОНЧАТЕЛЬНЫЙ Уравнение высоты.pdf, Школа, как основное условие психологического развития младших шк, Решение задач Волкенштейн 1.24 Зависимость пройденного телом пут, Метод изоклин Дифференциальное уравнение первого порядка.docx, квадратное уравнение.docx, Особенности профессии юриста и её основное нравственное значение, Основное уравнение РЛ.docx по дисциплине: Теплофизика на тему: Уравнение Клапейрона-Менделеева. Основное уравнение молекулярно-кинетической теории идеальных газов Заочной формы обучения Содержание
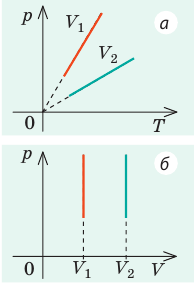
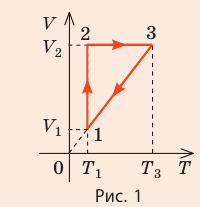
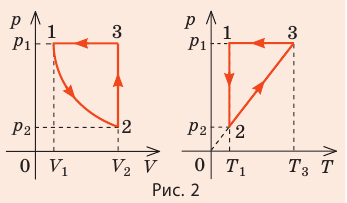
Видео:Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать  Оглавление1. От законов к уравнению 4 2. Идеальное соотношение для идеальных газов 7 3. Почему оно идеальное 8 Список использованных источников 11 Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать  ВведениеСегодня ни физика, ни химия, ни любая другая естественная наука немыслима без этой универсалии – уравнения состояния идеального газа. В современной науке это уравнение носит название «уравнение Менделеева-Клапейрона». Действительно, оба ученых независимо друг от друга по сути вывели это уравнение из имеющихся на том этапе данных о свойствах идеальных газов. На практике идеальных газов не существует, как, наверное, не существует вообще ничего идеального. Однако многие газообразные вещества при определенных условиях проявляют свойства как бы идеальных газов. и весьма замечательно их состояние описывается известным не только великим умам современности, но и почти каждому школьнику уравнением. Цель реферативной работы – раскрыть сущность уравнения Менделеева-Клапейрона и оценить огромное значение этого нехитрого соотношения для современной науки. Задачами реферативной работы стали: — проведение исторического экскурса, — объяснение формулы, являющейся основой уравнения, — определение значимости уравнения для науки. При написании работы использовались труды самого Д.И. Менделеева, а также современных исследователей: Чугаева, Храмова, Дрофмана, Левченкова. Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать  1. От законов к уравнениюК концу XVIII века наука встала на иной путь – путь непрерывного развития и совершенствования. Это происходит потому, что общество постепенно избавлялось от невежества и примитива, внушенных религиозным сознанием, и переходило от нелепых фантазий к исследованиям. Повсюду открываются научные школы, появляются первые труды ученых мужей, они публикуются без цензуры, вне страха перед кострами инквизиции. Мир познается не наощупь и не в религиозном бреду, а на основе наблюдений и размышлений. Конечно, предрассудки еще царствовали в умах даже тех, кто пытался перевернуть с ног на голову мировоззрение. Эти предрассудки тормозили научный прогресс, не давали смелым мыслям вырываться наружу. По-прежнему в ход пускалась фантазия, что-то домысливали, что-то оставляли на половине пути, так и не исследовав. Но механизм был запущен. Развитие науки было уже не остановить. К концу XVIII века были созданы все предпосылки для исследований в области газообразных веществ. Газы всегда интересовали ученых своей загадочностью: ведь это были весьма «непослушные» вещества, которые «не хотели», чтобы их исследовали. Ведь газ сначала надо было поймать, потом постараться удержать, не теряя ни молекулы. Тем не менее экспериментальная работа велась, и велась она уже с XVI века. Начало пути к известному уравнению открыл английский ученый Роберт Бойль. Удивительно, но этот человек, положивший начало многочисленным исследованием в области газов, был религиозен, и более того, он занимался миссионерской деятельностью. Трудно было представить в те времена человека, который бы с равным рвением утверждал, что Христос в теле поднялся на небо, и что «при постоянной температуре и массе газа произведение давления на его объем остается постоянным»[8]. А ведь именно так Бойль в 1662 году сформулировал свой знаменитый закон, который впоследствии был назван законом Бойля-Мариотта, поскольку четырнадцать лет спустя этот закон будет сформулирован французским физиком Эдмом Мариоттом. Поскольку ученые работали независимо друг от друга, а Эдм Мариотт ничего не знал об открытии своего коллеги из Англии, — то патент на открытие по праву принадлежит им обоим[2]. Если давление газа – существенный для газообразного вещества параметр – обозначить P, а не менее важный для газа параметр – объем обозначить V, то закон Бойля-Мариотта будет записан в виде формулы: Мариотт пошел дальше Бойля – он привел иную формулировку закона. Сначала он ввел понятие «состояние газа». Состояние газа – это набор определенных параметров: давления (P), объема (V) и температуры (T).Предположим, что газ перевели из состояния (1) в состояние (2) (сжали, расширили), сохраняя при этом постоянной температуру. Теперь газ будет характеризовать другими значениями давления и объема. Из состояния с давлением P1и объемом V1 он перешел в состояние с давлением P2 и объемом V2. При этом произведение PV не изменится. Учитывая соотношение /1.1/, можно записать: Напишем это соотношение так: Это соотношение и лежит в основе формулировки Мариотта: «Давление некоторой массы газа, находящегося при постоянной температуре, обратно пропорционально его объему». Закон Бойля-Мариотта действует исключительно в изотермических условиях. А как быть с теми условиями, когда, например, газ нагревается при постоянном давлении? На это вопрос ответил в начале, правда, уже XIXвека французский ученый Жозеф Луи Гей-Люссак. Он сформулировал закон, отражающий отношение между параметрами газа при постоянном давлении. Если давление постоянно, то при переходе газа из одного состояние в другое меняются лишь объем и температура. Гей-Люссак сформулировал этот закон как закон обратной пропорциональности между объемом и температурой газа при постоянном давлении. Если с формулировкой закона было вроде бы все ясно, то – вот парадокс! – совсем плохи дела обстояли с наименованием закона. Закон объемов (так назывался закон Гей-Люссака) впервые был опубликован в открытой печати в 1802 году Гей-Люссаком , однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году . Независимо от них закон был открыт в 1801 году английским физиком Джоном Дальтоном . Кроме того, качественно закон был описан французом Гийомом Амонтоном в конце XVII века. Пока ученые делили между собой славу открытия, закон уже вовсю работал на ниве теории идеальных газов. Математически его может выразить любой среднестатистический школьник: Оставалось лишь понять, как объединить все три параметра: объем, давление, температуру. В 1811 году итальянец Амедео Авогадро на основе некоторых экспериментов показал, что «число молекул всегда одно и то же в одинаковых объемах любых газов». Эта формулировка стала законом Авогадро. За нее-то и зацепился Бенуа Поль ЭмильКлапейрон. И на основе объединения законов Бойля-Мариотта и Гей-Люссака, применяя закон Авогадро, он определил, что для данной порции любого газа отношение Итак, от законов, сформулированных для идеальных газов, был осуществлен переход к формуле. Закона Клапейрона существовать никогда не будет. Зато будет существовать формула, которая станет наиважнейшей формулой теории идеальных газов. Видео:Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать  2. Идеальное соотношение для идеальных газовВеликое открытие в теории идеальных газов было сделано Клапейроном в 1834 году. Сорок лет спустя великий Менделеев не оставит это открытие без внимания. В 1874 году (уже после открытия Периодического Закона) Дмитрий Иванович определит, наконец, что же это за загадочная постоянная, держащая в узде три параметра газообразного вещества: объем, давление и температуру. В результате многочисленных опытов, Менделеев установит, что соотношение Но это – для одного моля газа. А если количество газообразного вещества больше или меньше? Знаменитый гений и здесь не замялся, и быстро ответил: «Ну… тогда универсальную газовую постоянную надо умножить на количество!»[10]. Теперь формула /1.6/ еще более конкретизируется:/1.7/, где Но количество вещества газа связана с его массой соотношением: Уравнение /1.9/ и называется уравнением Менделеева-Клапейрона. Его другое название – уравнение состояние идеального газа. Оно настолько точно описывает поведение идеальных газов, что вправе получить эпитет «идеальное» уравнение. Видео:Уравнение состояния идеального газа. 10 класс.Скачать  3. Почему оно идеальноеНе надо быть великим математиком, чтобы понять, какие интересные величины можно вывести из уравнения состояния идеального газа. Во-первых, само уравнение позволяет найти любой параметр газа, если известны его масса и два других параметра. Если преобразовать уравнение, то можно найти много интересных величин. Например, плотность газа при определенных условиях. Плотность газа – это отношение массы газа к его объему, то есть ⍴ = Наконец, любому школьнику будет интересно знать, откуда же берется это число 22,4, о котором учитель химии на уроке все уши прожужжала. Чтобы вести расчеты с газами, необходимо хотя бы образно привести их к одинаковым условиям, иначе получится нелепица и чехарда. Обычно относят к так называемым «нормальным условиям», при которых давление P = 101,325 кПа, температура T = 273 К (0 градусов по шкале Цельсия). А 22,4 – это величина молярного объема – объема, который занимает 1 моль любого газа. Применяем наше идеальное уравнение Подставляем единицу в формулу V = В объем данной работы не может войти всех областей применения идеального уравнения для идеальных газов. А их очень много! Видео:Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать  ЗаключениеТаким образом, уравнение состояния идеального газа отражает взаимосвязь между его параметрами и массой. Поскольку любой газ при достаточно низких давлениях ведет себя почти «идеально», то следует вывод, что уравнение Менделеева-Клапейрона универсально. Оно применимо и в области повышенных давлений, только с известными поправками. Уравнение Менделеева-Клапейрона с успехом применяется не только в теории газов, но и в термодинамике, теплотехнике. Его вездесущность трудно переоценить. Оно позволяет найти дополнительные величины, которыми характеризуется газообразное вещество. В заключение хочется привести известную фразу Дмитрия Ивановича Менделеева:«Наука начинается с тех пор, как начинают измерять. Точная наука немыслима без меры». Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать  Закон Клапейрона-Менделеева для идеального газа: исторические предпосылки, формула, пример задачиРассмотрение свойств газов в физике в первом приближении основывается на концепции идеального газа. В данной статье подробно изучим эту концепцию и приведем уравнение, которое описывает численно термодинамические свойства упомянутой текучей субстанции. Это уравнение называется законом Клапейрона-Менделеева. Видео:62. Уравнение Клапейрона-МенделееваСкачать  Концепция идеального газаВ школьном курсе физики газовое агрегатное состояние вещества характеризуется произвольным перемещением с различными скоростями всех составляющих его атомов и молекул. Эти частицы считаются в первом приближении абсолютно упругими материальными точками. Они имеют массу, но не размеры. Весь характер их взаимодействия друг с другом заключается в абсолютно упругих столкновениях, в результате которых сохраняется количество движения и энергия. Все перечисленные свойства частиц и их приближения образуют концепцию идеального газа. Любой реальный газ, будь то гелий, кислород или воздух, можно с высокой точностью считать идеальным, если его давление составляет порядка одной атмосферы и ниже, а температура соответствует комнатной или выше. Если эти условия не выполняются, то газ считается реальным, и для его описания следует использовать уравнение Ван-дер-Ваальса, а не закон Клапейрона-Менделеева, о котором пойдет речь далее в статье. Видео:Физика. Уравнение Менделеева-Клапейрона . МКТСкачать  Предпосылки возникновения уравнения состояния идеального газаПод уравнением состояния газа идеального принято понимать математическую формулировку газового закона Менделеева-Клапейрона. Как и любое открытие в физике, это уравнение не появилось из неоткуда, а имело вполне определенные исторические предпосылки. В 60-70-е годы XVII века англичанин Роберт Бойль и француз Эдм Мариотт независимо друг от друга в результате многих проведенных экспериментов с различными газами установили, что произведение объема на давление для закрытой системы с газом остается постоянным для любых процессов, в результате которых температура не изменяется. В настоящее время этот газовый закон носит фамилии названных ученых. Спустя почти 1,5 века, в конце XVIII — начале XIX веков французы Шарль и Гей Люссак открывают еще два экспериментальных закона в поведении идеальных газов. Они устанавливают прямо пропорциональную зависимость между давлением и температурой при постоянном объеме и между объемом и температурой при постоянном давлении. Наконец, в 1834 году Эмиль Клапейрон вывел, анализируя открытые предыдущими учеными газовые законы, уравнение Клапейрона. Менделеева фамилия появилась в названии этого уравнения благодаря его вкладу в преобразование исходного выражения к современному виду. В частности, Менделеев ввел понятие универсальной газовой постоянной. Видео:Решение графических задач на тему Газовые законыСкачать  Формула закона Клапейрона-МенделееваВыше мы дали определение идеального газа, рассказали о законах, которые привели к формулировке универсального уравнения состояния. Теперь пришло время записать это уравнение: Здесь P, V, n и T — давление, объем, количество вещества и температура, соответственно. Таким образом, произведение объема системы на давление в ней всегда находится для идеального газа в прямой пропорциональности произведению абсолютной температуры на количество вещества. Коэффициентом пропорциональности является уже упомянутая универсальная постоянная R. Она равна 8,314 Дж/(моль*К). Если 1 моль газа нагреть на 1 кельвин, то в процессе расширения он совершит работу 8,314 Джоуля. Любопытно заметить, что универсальной величина R называется потому, что она не определяется химической природой газа. Для всех чистых газов и их смесей она принимает единственное значение. Видео:Урок 178. Тепловые двигатели и их КПД. Цикл КарноСкачать  Откуда выводится изучаемое уравнение?Выше мы уже сказали, что Клапейрон свое уравнение получил в результате банального обобщения экспериментальных результатов различных ученых. Тем не менее, закон Клапейрона-Менделеева может быть получен чисто теоретическими методами. Одним из них является МКТ (молекулярно-кинетическая теория). МКТ рассматривает газовую систему с точки зрения концентрации частиц, распределения их скоростей, учета их масс и следование концепции идеального газа. Универсальное уравнение газа однозначно следует, если применить второй закон Ньютона к процессу упругого соударения частиц со стенками герметичного сосуда. В результате применения МКТ получается выражение: Это равенство приводит к записанному в предыдущем пункте уравнению, если учесть следующие выражения: Видео:Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать  Использование универсального уравнения для решения задачиИзвестно, что некоторый газ под давление 2 атмосферы находится в баллоне при температуре 25 o C. Объем баллона составляет 50 литров. Какое количество вещества содержится в баллоне? Поскольку нам известны 3 из 4-х параметров, то можно применить закон Клапейрона-Менделеева, чтобы найти величину n. Прежде чем это сделать, переведем все единицы в систему СИ: T = 25 + 273,15 = 298,15 К; Теперь воспользуемся формулой, получим: n = P*V/(R*T) = 202650*0,05/(8,314*298,15) = 4,09 моль. Хотя само значение 4,09 моль является небольшим, количество частиц газа будет гигантским. Чтобы его получить, следует n умножить на NA=6,02*10 23 . Видео:Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать  Уравнение состояния идеального газа — основные понятия, формулы и определение с примерамиСодержание: Уравнение состояния идеального газа: Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда. Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать  Уравнение состояния идеального газаДавление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения Произведение числа Авогадро Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона. Уравнение КлапейронаС помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния ( Для каждого состояния запишем уравнение Менделеева — Клапейрона: Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным. ИзопроцессыПроцесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их. Какой процесс называют изотермическим. Закон Бойля — МариоттаПузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды ( Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре. Пусть некий газ переходит из состояния ( Закон Бойля — Мариотта: Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется: Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: Какой процесс называют изобарным. Закон Гей-ЛюссакаИзобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении. Пусть некий газ переходит из состояния ( Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p Закон Гей-ЛюссакаДля данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется: Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в). Изохорный процесс. Закон ШарляЕсли газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием. Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме. Пусть некий газ переходит из состояния ( Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно: Закон ШарляДля данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется: Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в). Пример №1В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов? Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется: Решение: Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: Ответ: примерно в 2,7 раза. Пример №2На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T. Решение: 1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1). Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ . 2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 🎦 ВидеоФизика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать  Уравнение Менделеева-Клапейрона.Все виды задач на ЕГЭ.52 задачиСкачать  Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать  Ковалентная Полярная Связь — Химическая связь // Химия 8 классСкачать  Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать  Уравнение Менделеева-Клапейрона и 4 изопроцесса для состояния идеального газа (графики и смысл).Скачать  |
 /1.1/
/1.1/ /1.2/
/1.2/ /1.3/
/1.3/ /1.4/,
/1.4/,  /1.5/
/1.5/ остается постоянным, даже если менять параметры[9].
остается постоянным, даже если менять параметры[9]. /1.6/.
/1.6/. как раз то пресловутое количество газа, на которое предлагал умножить универсальную газовую постоянную Менделеев[7].
как раз то пресловутое количество газа, на которое предлагал умножить универсальную газовую постоянную Менделеев[7]. /1.8/. Объединяя соотношения /1.7/ и /1.8/, получим:
/1.8/. Объединяя соотношения /1.7/ и /1.8/, получим:  /1.9/.
/1.9/. /1.10/. В уравнении /1.9/ можно эту плотность определить:
/1.10/. В уравнении /1.9/ можно эту плотность определить:  .
. , и первое, что видим, так это:
, и первое, что видим, так это:  .
. =
=  = 22,4 (л/моль).
= 22,4 (л/моль).

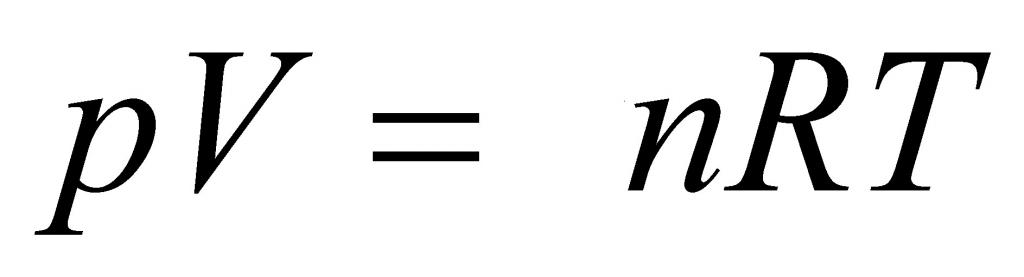

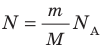
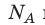 на постоянную Больцмана k называют универсальной газовой постоянной (R): R=
на постоянную Больцмана k называют универсальной газовой постоянной (R): R=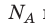 k 8,31 Дж/ (моль⋅К). Заменив в уравнении (*)
k 8,31 Дж/ (моль⋅К). Заменив в уравнении (*) 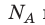 k на R, получим уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
k на R, получим уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):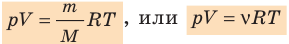
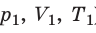 ) в состояние (
) в состояние (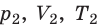 ) (рис. 30.1).
) (рис. 30.1).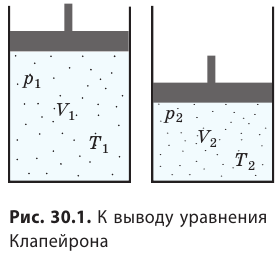
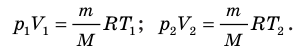 Разделив обе части первого уравнения на
Разделив обе части первого уравнения на 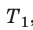 , а второго — на
, а второго — на 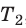 , получим:
, получим: 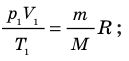
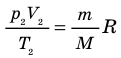 . Правые части этих уравнений равны; приравняв левые части, получим уравнение Клапейрона:
. Правые части этих уравнений равны; приравняв левые части, получим уравнение Клапейрона: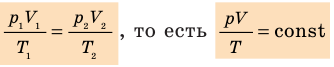
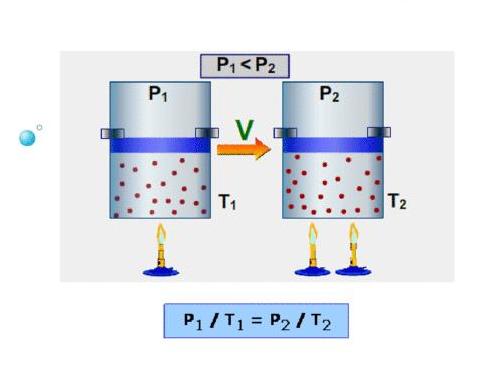
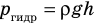 ) давление на глубине больше атмосферного. Температура же внутри пузырька практически не изменяется. В данном случае имеем дело с процессом изотермического расширения.
) давление на глубине больше атмосферного. Температура же внутри пузырька практически не изменяется. В данном случае имеем дело с процессом изотермического расширения.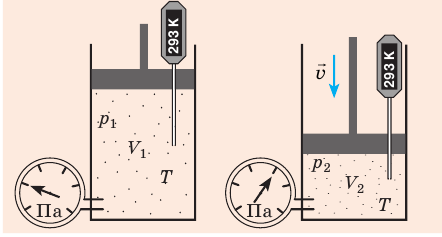
 ) в состояние (
) в состояние (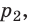
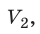 T), то есть температура газа остается неизменной (рис. 30.2). Тогда согласно уравнению Клапейрона имеет место равенство p
T), то есть температура газа остается неизменной (рис. 30.2). Тогда согласно уравнению Клапейрона имеет место равенство p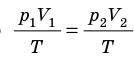 . После сокращения на T получим:
. После сокращения на T получим: 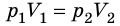 .
.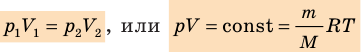
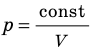 . Эту зависимость в координатах p, V можно представить в виде гиперболы (рис. 30.3, а). Поскольку при изотермическом процессе температура газа не изменяется, в координатах p, T и V, T изотермы перпендикулярны оси температур (рис. 30.3, б, в).
. Эту зависимость в координатах p, V можно представить в виде гиперболы (рис. 30.3, а). Поскольку при изотермическом процессе температура газа не изменяется, в координатах p, T и V, T изотермы перпендикулярны оси температур (рис. 30.3, б, в).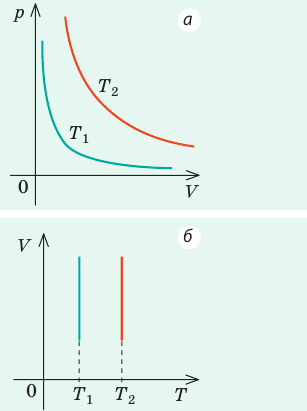

 ) в состояние (
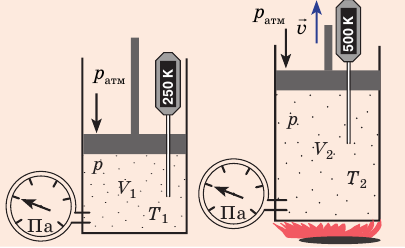
) в состояние (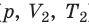 ), то есть давление газа остается неизменным (рис. 30.4). Тогда имеет место равенство
), то есть давление газа остается неизменным (рис. 30.4). Тогда имеет место равенство 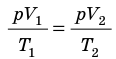 . После сокращения на p получим:
. После сокращения на p получим: 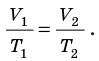
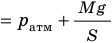
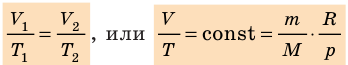
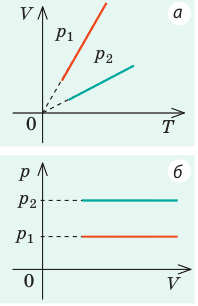

 ) в состояние (
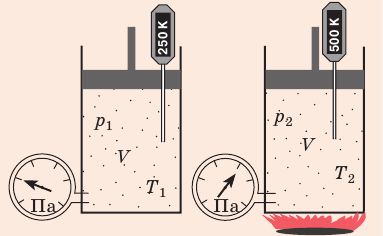
) в состояние (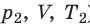 ), то есть объем газа не изменяется (рис. 30.6). В этом случае имеет место равенство
), то есть объем газа не изменяется (рис. 30.6). В этом случае имеет место равенство 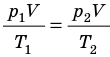 . После сокращения на V получим:
. После сокращения на V получим: 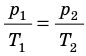
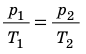
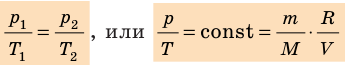

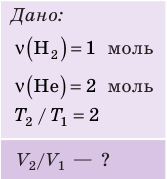
 , но использовать закон Бойля — Мариотта нельзя, так как вследствие диссоциации (распада) молярная масса и число молей водорода увеличились в 2 раза:
, но использовать закон Бойля — Мариотта нельзя, так как вследствие диссоциации (распада) молярная масса и число молей водорода увеличились в 2 раза: 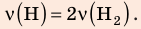
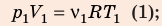
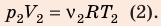 Разделив уравнение (2) на уравнение (1) и учитывая, что
Разделив уравнение (2) на уравнение (1) и учитывая, что 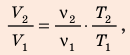 где
где 
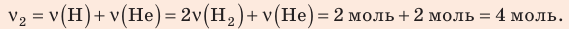 Найдем значение искомой величины:
Найдем значение искомой величины: 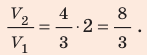
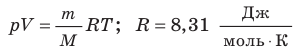 — универсальная газовая постоянная.
— универсальная газовая постоянная.