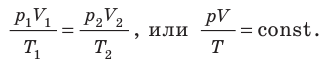Из уравнений (1.8.1) и (1.8.7) следует, что
Учитывая, что n = N/V и N/NА = m/μ = ν, получим

где введена постоянная R=kNA=8,31Дж/мольּК, которую называют универсальной газовой постоянной. Физический смысл ее установим из уравнения (1.9.2):

которое называют уравнением Менделеева – Клапейрона. Для этого запишем уравнение (1.9.3) для двух состояний изобарического процесса:
 |
Откуда находим

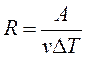
т. е. постоянная R численно равна работе при изобарическом нагревании на один Кельвин (ΔТ = 1К) одного моля (ν = 1моль) идеального газа. Так как k = R/NA, то постоянная Больцмана имеет тот же смысл, что и R, только рассчитанная на одну молекулу.
Из уравнения состояния идеального газа (1.9.3) можно получить известные из опыта газовые законы.
1. Полагая в уравнении (1.9.3) ν = const и Т = const, получаем
Отсюда вытекает формулировка закона Бойля – Мариотта (изотермический процесс): при неизменных массе и температуре идеального газа произведение его объема на давление есть величина постоянная.
2. При изобарическом процессе P = const.Также ν = сonst. Поэтому из уравнения состояния (1.9.3) в этом случае

т. е. при неизменных массе и давлении идеального газа отношение объема, занимаемого газом, к его температуре – величина постоянная. Это утверждение известно как закон Гей-Люссака.
3. Пусть процесс протекает при постоянном объеме V=const (по
прежнему ν = сonst). Тогда из (1.9.3)

т. е. при неизменных массе и объеме идеального газа отношение давления газа к его температуре есть величина постоянная. Уравнение (1.9.8), называемое уравнением изохорического процесса, выражает известный закон Шарля.
4. Из уравнения (1.9.3), очевидно, также следует объединенный закон
Мариотта – Гей- Люссака

т. е. произведение давления газа на его объем, деленные на абсолютную температуру, для данной массы газа есть величина постоянная.
5. Из уравнения (1.9.3) также следует закон Авогадро, согласно которому при одинаковых давлениях и температурах в равных объемах любого газа содержится одинаковое число молекул. Действительно, пусть имеются два одинаковых объема двух различных газов при одинаковых давлениях и температурах. Для каждого из них можно написать уравнение состояния (1.9.2)
где N1 и N2 – число молекул обоих газов. Из этих равенств непосредственно следует, что N1= N2. Это и есть закон Авогадро. Из него, очевидно, следует и обратная формулировка: различные газы, но содержащие одинаковое число молекул, будут при одинаковых давлениях и температурах занимать одинаковые объемы. Поэтому моль любого газа при данных давлении и температуре занимает одинаковый объем. В частности, при нормальных условиях (Т0= 273,15К, Ратм= 1,01ּ10 5 -Па) моль любого газа занимает объем

6. Следствием уравнения идеального газа является и закон Дальтона, утверждающий: давление смеси химически не реагирующих газов равно сумме парциальных давлений отдельных газов. Парциальным давлением называют давление, которое создал бы газ, если бы он находился один в объеме, занятом смесью.
Для доказательства закона Дальтона учтем, что в смеси нескольких газов общее количество молекул равно сумме количеств молекул отдельных газов
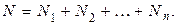
Подставим (1.9.10) в (1.9.3)

Каждое из слагаемых выражения (1.9.11) представляет собой парциальное давление. Поэтому

Что и требовалось доказать.
7. Наконец, следствием уравнения Менделеева – Клайперона является закон Амага: объем смеси химически нереагирующих идеальных газов равен сумме их парциальных объемов, т. е.

где парциальный объем

Как видно из выражения (1.9.14), парциальный объем Vi есть объем, который занимал бы i-й газ, если бы все остальные газы были удалены, а давление Р и температура Т остались неизменными.
Для доказательства найдем из уравнения (1.9.2) идеального газа объем смеси

и подставим в него вместо N его выражение из (1.9.15). В результате получим
что и доказывает справедливость закона Амага.
1. Доказать, что молекулы любых газов при одинаковых температурах обладают одинаковой средней кинетической энергией поступательного движения.
Решение. Выражение (1.5.9): 




Если температуры этих газов одинаковы, то
где
Как видно из доказательства, средняя кинетическая энергия поступательного движения не зависит от массы и внутренней структуры молекулы. Поэтому ее выбирают в качестве меры нагретости
Следует обратить внимание на тот факт, что средние кинетические энергии вращательного и колебательного движений молекулы не могут быть взяты за меру температуры газа, так как эти энергии зависят не только от температуры, но и от параметров, характеризующих структуру молекулы – ее момента инерции и частот колебаний атомов в молекуле.
2. Земная атмосфера состоит из смеси различных газов, которые на уровне моря по объему составляют (при нормальных условиях): азот – 78,09 %, кислород – 20,95 %, аргон – 0,93 %, углекислый газ – 0,03 %, неон – 0,0018 %. Остальными компонентами (водород, гелий, ксенон, криптон, метан и др.) пренебрегают, так как они составляют миллионные доли процента. Найти молярную массу воздуха.
Решение. Пусть взято количество воздуха массы 

Выражая отношения масс через отношение плотностей и объемов 
где 
V4/V = 0,0003, V5/V = 0,000018, а также, взятые из таблиц, опытные значения (при нормальных условиях) плотностей азота ρ1= 1,250 кг/м 3 , кислорода
ρ2= 1,429 кг/м 3 , аргона ρ3= 1,784 кг/м 3 , углекислого газа ρ4= 1,977 кг/м 3 , неона ρ5= 0,900 кг/м 3 воздуха ρ=1,293 кг/м 3 и молярные массы компонентов воздуха μ1= 28·10 – 3 кг/моль,μ2= 32·10 – 3 кг/моль, μ3= 40·10 – 3 кг/моль,μ4=
= 44·10 – 3 кг/моль, μ5= 20·10 – 3 кг/моль,получим молярную массу воздуха μ =
= 0,02896 ≈ 29·10 – 3 кг/моль.
Распределение Максвелла
В газе, находящемся в равновесии при температуре T, скорость любой молекулы из-за столкновений непрерывно меняется как по абсолютной величине, так и по направлению. Распределение по направлениям движения в состоянии равновесия равновероятно. Если бы это было не так, то в каком-то направлении в газе двигалось бы большее число молекул, чем в другом. В результате возник бы макроскопический поток газа и газ не находился бы в равновесии.
Иначе обстоит дело с абсолютными значениями скоростей молекул: они не будут равновероятны, т. е. функция плотности вероятности F(υ) принимает неодинаковые значения при различных скоростях молекул. При этом, наибольшее число молекул будет группироваться около некоторой средней скорости, к примеру, около средней квадратичной υкв, которая на основании формулы (1.8.7),

Очень большие скорости молекул, по сравнению со средней квадратичной, маловероятны. В самом деле, чтобы молекула могла приобрести при столкновениях очень большую скорость, ей необходимо испытать подряд много таких столкновений, при которых она в основном получает энергию, и почти ни одного столкновения, при котором она ее теряет. Но такие столкновения маловероятны. Поэтому значения функции F(υ) при больших скоростях должны быть малы.
Функция F(υ) в равновесном состоянии газа не должна зависеть от времени. В самом деле, если бы функция распределения зависела от времени, то средняя квадратичная скорость, определяемая по формуле,

также зависела бы от времени. Но это противоречит тому, что в состоянии равновесия (T = const), как видно из (1.10.1), υкв= сonst.
Таким образом, распределение молекул по скоростям должно иметь максимум около среднего квадратичного значения скорости и убывать до нуля от этого максимального значения в сторону больших скоростей молекул. Найдем, следуя Максвеллу, явный вид этой функции.
Спроектируем скорости всех N молекул газа на ось x. Вероятность того, что произвольно взятая молекула имеет проекцию скорости, заключенную в интервале (υx , υx+ dυx), будет равна
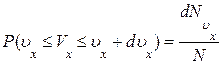
где 

Сравнивая выражения (1.10.2) и (1.10.3) , находим

Аналогичные соотношения могут быть записаны для проекций скоростей молекул на оси Y и Z.
Важно отметить, что функции 


Запишем далее вероятность того, что случайно взятая молекула имеет проекции скорости, заключенные в интервалах (υx, υx + dυx), (υy, υy + dυy) и (υz, υz + dυz) или, то же самое, что эта молекула движется в направлении, близком к направлению, определяемом вектором 

где 


Из выражений (1.10.5) и (1.10.6) следует, что

Чтобы дать наглядное представление о функции 




Функция 


где 
Наряду с введенными функциями φ и f, рассмотрим распределение молекул F(υ) по абсолютной величине скорости. Распределение F(υ)определяется вероятностью того, что величина скорости молекулы заключена в пределах от υ до υ + dυ независимо от направления, т. е.

где 
Функции F(υ) и f(υ) жестко связаны друг с другом. Для определения этой связи обратимся к пространству скоростей. Очевидно, в этом пространстве число скоростных точек, попадающих в шаровой слой между сферами радиусов υ и υ+dυ, объем которого 


Подставив 

Далее Максвелл предположил, что события, заключающиеся в попадании проекций υx, υy, υz скорости данной молекулы в интервалы
(υx, υx + dυx), (υy, υy + dυy) и (υz, υz + dυz)соответственно, являются независимыми событиями. Тогда, согласно теореме умножения, совместная вероятность этих событий равна произведению их вероятностей, т. е.

На основании формул (1.10.6) и (1.10.3), равенство (1.10.11) можем переписать в виде:

Разделив обе части (1.10.12) на 


Прологарифмируем последнее равенство

Дифференцируя выражение (1.10.14) на компоненте скорости υx , получим

Учитывая, что 

Это позволяет записать соотношение (1.10.15) в виде

Аналогичные выражения могут быть получены при дифференцировании (1.10.14) по двум другим компонентам скорости υy и υz:

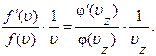
Правые части этих равенств равны друг другу, так как левые части их одинаковы. Правая часть (1.10.17) не зависит от υy и υz. Значит, от них не зависит и левая часть. Аналогично, правая часть (1.10.18) не зависит от υx и υz, откуда следует независимость и левой части от этих величин. Но тогда и правая часть (1.10.17) не зависит от υх. Это возможно только в том случае, если

Умножим обе части (1.10.20) на υхdυх. В результате будем иметь




Из-за равной вероятности направлений движения молекул точно такой же вид имеют функции 



Второе уравнение – это связь средней кинетической энергии поступательного движения молекулы с температурой:

Как было выяснено ранее, очень большие скорости молекул должны быть маловероятными. Это возможно только в том случае, если постоянная в формуле (1.10.24) отрицательна, т. е.

В выражении (1.10.25) максимально возможная проекция на ось Х скорости молекул, находящихся при температуре T, положена равной бесконечности, что физически нереально. Однако увеличение интервала интегрирования сверх некоторой максимальной скорости не приведет к заметной ошибке ввиду того, что функция (1.10.27) быстро убывающая.
Подставляя (1.10.27) в (1.10.25) и интегрируя (см. формулу (B.2) приложения B), получим

Откуда находим 

Чтобы воспользоваться равенством (1.10.26) для нахождения постоянной С1учтем, что

так как ввиду равновероятности направлений движения молекул 



Используя формулы (1.10.31), (1.10.30) и (1.10.26), находим

Подстановка постоянной (1.10.32) в (1.10.29) дает

Точно такие же формулы будут справедливы и для других проекций скорости молекул. Поэтому функция (1.10.13)

а функция распределения по абсолютным значениям скорости (1.10.10)

Как это мы уже отмечали при выводе распределений (1.10.33–1.10.35) по скоростям, Максвеллом было сделано предположение: проекции скорости молекул статистически независимы. Это предположение им не было доказано или обосновано. В дальнейшем американским физиком-теоретиком Д. Гиббсом было доказано, что условие независимости компонент скорости имеет место тогда, когда кинетическая энергия квадратична по компонентам импульсов; последнее справедливо всегда, за исключением случая релятивистских скоростей частиц.
Очень важно отметить, что при доказательстве распределения Максвелла (1.10.33–1.10.35) не делалось никаких предположений относительно структуры молекул, сил взаимодействия между ними, поэтому они справедливы не только для газов, но и для жидкостей, для твердых тел и, даже, для броуновских частиц, если при этом возможно классическое описание.
Как доказывается в статистической физике, классический способ изложения применим, если температура Т равновесного состояния системы частиц значительно больше так называемой температуры вырождения

где h и k – постоянные Планка и Больцмана, m0 – масса частицы, n – концентрация частиц.
Систему частиц, находящуюся при температуре T 3 огромно и имеет порядок 10 29 Z, где Z – валентность металла. Вычисления по формуле (1.10.36) дают TB
10 4 K. Поэтому при условиях близким к нормальным электронный газ в металлах является вырожденным и к нему неприменима статистика Максвелла. Она, как доказывается в квантовой физике, должна быть заменена на статистику Ферми – Дирака.
Однако электроны, эмитируемые с раскаленного металла в вакуум, образуют электронный газ, скорости частиц которого уже будут распределены по закону Максвелла, т. к. их концентрация n значительно меньше, чем в металле, и соотношение (1.10.36) будет выполнено.
В качестве второго примера рассмотрим водород, который при нормальных условиях имеет концентрацию n0=2,7·10 25 м –3 . Вычисления по формуле (1.10.36) дают TB = 0,06 K. Так как все газы при нормальных условиях имеют одну и ту же концентрацию n0=2,7·10 25 м –3 , а массу молекул большую, чем масса молекулы водорода, то условие (1.10.36) будет выполнено и, таким образом, ко всем газам применима статистика Максвелла. Более того, непосредственным расчетом нетрудно показать, что к некоторым газам (углекислый газ, воздух, азот и др.), находящимся при низких температурах Т в жидком или твердом состоянии, распределения скоростей поступательного движения молекул, определяемые формулами (1.10.33–1.10.35), можно применять, т. е. в этом случае условие (1.10.36) будет выполнено.
- Уравнение Клапейрона-Менделеева
- Что такое уравнение Клапейрона-Менделеева
- Какое значение имеет универсальная газовая постоянная
- Связь с другими законами состояния идеального газа
- Изотермический процесс (T=const)
- Изохорный процесс (V=const)
- Изобарный процесс (p=const)
- Использование универсального уравнения для решения задачи
- Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- 📸 Видео
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение Клапейрона-Менделеева
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Что такое уравнение Клапейрона-Менделеева
Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.
Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.
Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.
Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.
Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:
p V = c o n s t * T
В представленном выше уравнении состоянии газа под const подразумевается количество молей.
Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.
p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.
Таким образом давление и объем прямо пропорциональны количеству молей и температуре.
Также уравнение Клапейрона-Менделеева можно записать в ином виде:
p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 — 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:
N = m N A M , где
N A = 6 . 02 * 10 23 м о л ь — 1 ; — это постоянная Авогадро.
Видео:Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

Какое значение имеет универсальная газовая постоянная
Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.
Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 — 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь — 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .
Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Связь с другими законами состояния идеального газа
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.
Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.
Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.
В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:
- изотермический процесс (T=const);
- изохорный процесс (V=const);
- изобарный процесс (p=const).
Изотермический процесс (T=const)
Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.
Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.
Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:
Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.
Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).
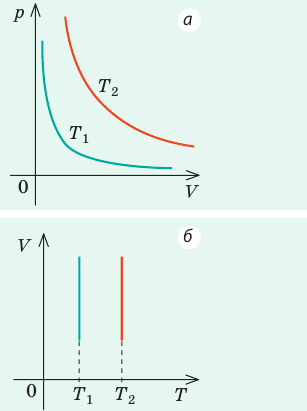
Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.
Рис.1. Изотерма в pV — координатах.
Изохорный процесс (V=const)
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.
Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:
p 1 p 2 = T 1 T 2
Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.
Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда
p = p 0 T T 0 = p 0 γ T
Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.
Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).
Рис.2 Изображение изохоры в pT-координатах.
Изобарный процесс (p=const)
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.
Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.
V 1 V 2 = T 1 T 2
Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:
V = V 0 T T 0 = V 0 α T
Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.
Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.
Коэффициент α называют температурным коэффициентом объемного расширения газов.
Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).
Рис. 3. Изобара в VT-координатах.
Видео:Решение графических задач на тему Газовые законыСкачать

Использование универсального уравнения для решения задачи
В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.
Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.
Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:
p V = n R T = m M R T
Не забываем перевести температуру в Кельвины:
T = t + 273 = 27 + 273 = 300 K
Молярная масса кислорода известна из таблицы Менделеева:
M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 — 3 к г / м о л ь
Выразим из уравнения состояния давления и поставим все имеющиеся данные:
p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 — 3 * 1 = 77 . 906 П а = 78 к П а
Ответ: p = 78 кПа.
Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?
Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:
p = n R T V = m R T M V
Молярная масса кислорода предполагается равной:
M ( O 2 ) = 2 * 16 = 32 г / м 3
Не забываем перевести температуру в Кельвины:
T = t + 273 = 20 + 273 = 293 K
Переводим давление: p = 15680000 Па
Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:
V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 — 3 = 3 . 1 * 10 — 2 м 3 = 31 л .
Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .
Согласно уравнению Менделеева-Клапейрона:
p = n R T V = m R T M V
Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:
ρ = m V и л и V = m ρ
Тогда p m ρ = n R T = m R T M
Откуда выражаем плотность газа:
Для водорода эта формула запишется следующим образом:
ρ H 2 = p M H 2 R T
По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:
ρ H 2 M H 2 = p R T
Поставим последнее выражение в выражение для плотности любого газа:
ρ = M * ρ H 2 M H 2
Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.
ρ = M r * ρ H 2 2
Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .
Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.
При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?
По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.
p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.
Откуда можем найти начальный объем:
p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V
V 1 ( p 1 — p 1 2 . 5 ) = p 1 2 . 5 ∆ V
p 1 2 . 5 V 1 ( 2 . 5 — 1 ) = p 1 2 . 5 ∆ V
V 1 = ∆ V 1 , 5 = 8 л
Ответ: первоначальный объем газа был равен 8 л.
Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?
Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.
При изохорном процессе:
p 1 T 1 = p 2 T 2
T 2 = p 2 T 1 p 1
p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K
При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?
Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.
V 1 V 2 = T 1 T 2
V_2 – искомый объем
Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:
T 1 = 273 + 27 = 300 K
T 2 = 273 + 57 = 330 K
T 2 V 1 T 1 = V 2
V 2 = ( 600 * 330 ) / 300 = 660 м л
Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.
Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:
V 1 V 2 = T 1 T 2
Перейдем к абсолютной температуре:
T 1 = 1150 + 273 = 1423 K
T 2 = 200 + 273 = 473 K
Масса газа: m = ρ 1 V 1 = ρ 2 V 2
Использование этих формул приводит к следующему:
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Видео:Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 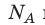
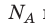
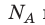
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
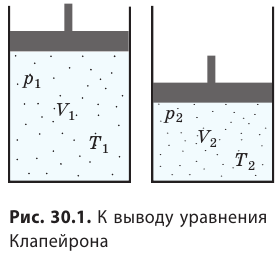
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (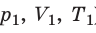
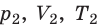
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 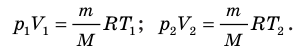
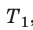
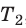
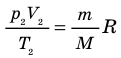
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (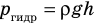
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (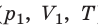
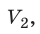
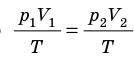
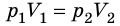
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 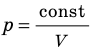
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (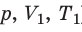
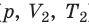
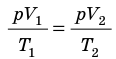
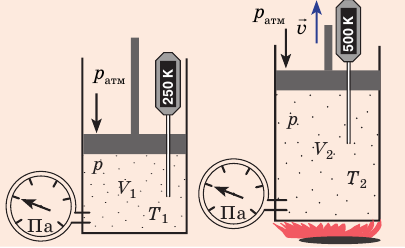
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
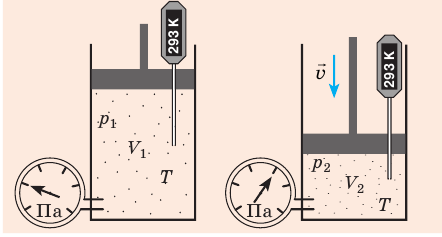
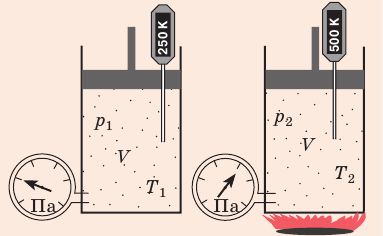
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (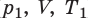
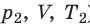
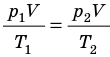
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
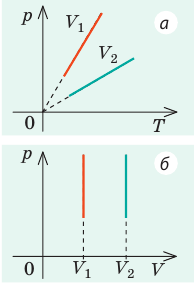
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 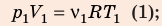
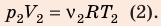

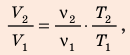
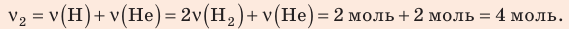
Ответ: примерно в 2,7 раза.
Пример №2
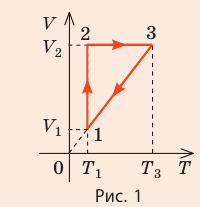
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
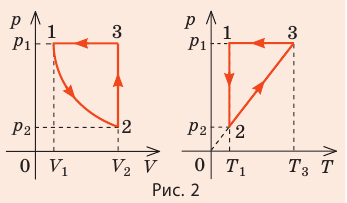
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📸 Видео
Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Урок 158. Задачи на газовые законы - 1Скачать

62. Уравнение Клапейрона-МенделееваСкачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать

Задачи на уравнение Менделеева-Клапейрона. Ч.2. Решение задач.Скачать

Уравнение Менделеева-Клапейрона.Все виды задач на ЕГЭ.52 задачиСкачать

Урок 149. Абсолютная температурная шкалаСкачать

Уравнение Менделеева-Клапейрона и 4 изопроцесса для состояния идеального газа (графики и смысл).Скачать

Вывод уравнения Менделеева-Клапейрона | Соня Бурулева | ФизикаСкачать

Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать











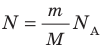
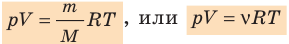
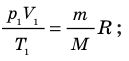
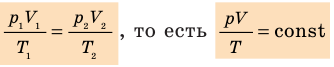
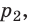
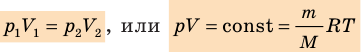

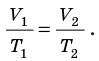
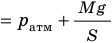
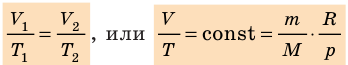
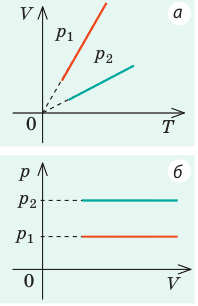

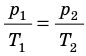
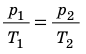
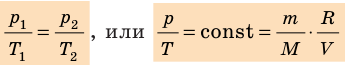

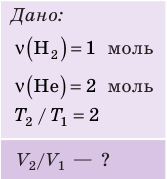
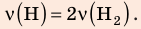

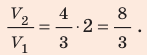
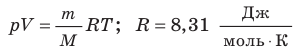 — универсальная газовая постоянная.
— универсальная газовая постоянная.