§ 12. Уравнения равномерного прямолинейного движения
1. Уравнение в векторной форме.
Знаем, что одна из основных задач механики заключается в нахождении положения точки в любой момент времени при движении. Знаем, что положение точки может быть определено радиус-вектором, и в любом движении конечный радиус-вектор имеет вид:

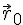
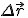
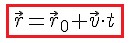
2. Уравнение в координатной форме.
Знаем, что векторы находят с помощью проекций на оси координат. Поэтому от векторного уравнения движения перейдём к проекциям векторных величин на оси координат.
Если 
.
Проекции радиусов равны соответствующим координатам. Поэтому:
.
Если траектория известна, то мы совмещаем траекторию с осью координат OX и пользуемся вместо трёх всего одним первым уравнением.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
- Механическое движение
- Механическое движение
- Прямолинейное равномерное движение
- Скалярные величины (определяются только значением)
- Векторные величины (определяются значением и направлением)
- Проецирование векторов
- Уравнение движения
- Прямолинейное равноускоренное движение
- Уравнение движения и формула конечной скорости
- Движение по вертикали
- Векторные формы уравнений движения
- Векторная форма уравнения движения
- Относительное движение массы
- 💡 Видео
Видео:Относительность механического движения. 7 класс.Скачать

Механическое движение
О чем эта статья:
Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Видео:Виды механического движенияСкачать
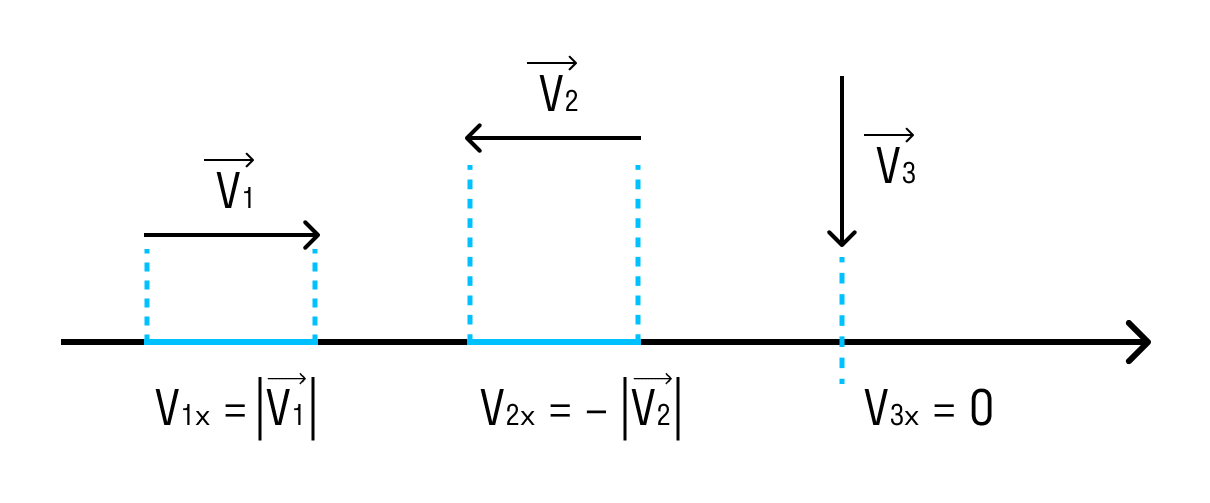
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Видео:Механическое движение | Физика 7 класс #9 | ИнфоурокСкачать

Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
| Сила левая | Сила правая |
| F grad | F eqw |
Проекция с уравнением является гидродинамическим уравнением Эйлера. Использование гидромеханики известных преобразований из векторного анализа это будет то же векторное уравнение или другая форма другой нотации.
Это движение считается связанным с выбранной системой отсчета на поверхности Земли или в центре массы Земли. Для инерциальной системы отсчета, уравнения движения в форме Эйлера линейно и равномерно в условиях «абсолютно неподвижного пространства», движение твердого тела описывается векторным уравнением.
Видео:Механическое движение. 9 класс.Скачать

Относительное движение массы
Здесь как основной вектор, так и угловой момент твердого тела относительно его центра масс являются основными векторами и моментами для центра масс всех внешних сил, действующих на твердое тело. Их следует считать не сплошными, а системой переменной конфигурации.
Для этого можно рассмотреть мгновенный затвердевший объект, применить силу реакции,силу внутри колориста, вариационную силу. Они представляют собой фиктивные «закаленные» объекты.
Внутренняя сила инерции кролика обусловлена относительным движением массы внутри твердой оболочки тела при вращении.Вариационная сила обусловлена нестационарным движением массы в твердой оболочке.
Часто совокупность сил: реактивная сила, статическая сила, возникающая из разности атмосферного давления уравнения движения в форме Ламба и давления газа на входе впускного отверстия и сопла воздухозаборника, и изменяющаяся сила объединяются и обозначаются вектором, называемым тяговым усилием двигателя. Иногда различают понятия двигателя и движителя.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
💡 Видео
ЕГЭ-1.3 . Кинематика. Уравнение равномерного прямолинейного движения в векторной форме.Скачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Относительность механического движения. Практическая часть - решение задачи. 7 класс.Скачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Траектория и уравнения движения точки. Задача 1Скачать

Урок 19. Относительность движения. Формула сложения скоростей.Скачать

Урок 12. Равномерное прямолинейное движениеСкачать

Урок 9. Проекции вектора на координатные осиСкачать

Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

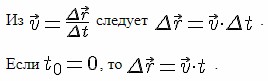
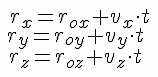 .
.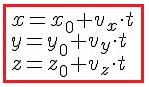 .
.