Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
3) Координаты точки C1 — середины отрезка BC:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Контрольная работа: Решение линейной системы уравнений с тремя неизвестными
| Название: Решение линейной системы уравнений с тремя неизвестными Раздел: Рефераты по математике Тип: контрольная работа Добавлен 01:23:41 11 марта 2010 Похожие работы Просмотров: 22082 Комментариев: 22 Оценило: 8 человек Средний балл: 4 Оценка: 4 Скачать | |||||||||||||||||||||||||||||
| х | (-¥; 1) | 1 | (1; 2) | 2 | (2; ¥) |
| f ’(x) | + | 0 | — | 0 | + |
| f(x) |  | max |  | min |  |
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
Итак, функция имеет одну критическую точку второго рода х = -1,5. Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:
| х | (-¥; 1,5) | 1,5 | (1,5; ¥) |
| f ‘’(x) | — | 0 | + |
| f(x) | Ç | т. п. | È |
Значение х = 1,5 является абсциссой точки перегиба графика функции, а ордината этой точки:
4) Выясним наличие у графика заданной функции асимптот. Для определения параметров уравнения асимптоты y = kx – b воспользуемся формулами
Таким образом, у графика заданной функции наклонных асимптот нет.
5) построим график функции
б)
1) Областью определения данной функции являются значения аргумента х
2) Исследование на непрерывность и классификация точек разрыва
Заданная функция непрерывна всюду, кроме точки х = 0. Вычислим ее односторонние пределы в этой точке:
Итак точка х = 0 – точка разрыва второго рода, а прямая х = 0 – вертикальная асимптота.
3) Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
Следовательно, функция не имеет критических точек первого рода.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение медианы ае и координаты точки
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
📸 Видео
Вычисляем высоту через координаты вершин 1Скачать

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение медианыСкачать

Уравнение окружности (1)Скачать

Составляем уравнение прямой по точкамСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

найти уравнение высоты треугольникаСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Три точки заданы координатами Найти длину медианы треугольникаСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

найти уравнения биссектрис углов между прямымиСкачать

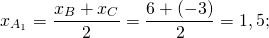
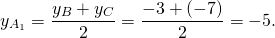
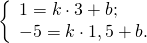
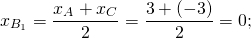
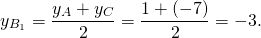
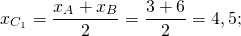
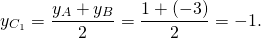
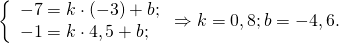











 соответствует множество решений системы линейных уравнений
соответствует множество решений системы линейных уравнений 





 , то есть
, то есть  откуда
откуда 

 , то есть
, то есть 












































 ; б)
; б) 














